多承载索货运索道计算方法及张力不平衡效应分析*

秦 剑，乔 良，江 明，郝玉靖

(中国电力科学研究院有限公司，北京100055)

0 引言

目前特高压输电线路路径多经过高山大岭、植被茂密等地形复杂恶劣的地区，且施工环保要求高，塔材、牵张设备、导线盘等施工用重型物资主要通过货运索道运输至指定位置，而现阶段输电线路施工中常用的简易货运索道的承载能力远不能满足相应的运载性能要求。因此，开展重型、超重型多承载索货运索道(以下简称为多索索道)的设计及安全性分析研究成为特高压输电线路工程运输施工技术中的重要发展方向[1]。

现有单承载索货运索道的计算方法主要分为解析法和有限元法。解析法主要包括悬链线法[2-3]和抛物线法[4]。悬链线法能够真实反映实际悬挂索结构的线形，按照悬链线方法理论计算得到的相关量被视为真值。抛物线法是悬链线理论取前二次项的近似计算方法。有限元法主要包括2节点杆单元[5-6]和多节点曲线单元[7]，均基于拉格朗日描述或欧拉描述进行分析。

抛物线法精度不足，无法满足工程要求；有限元法单元多，对于多承载索货运索道建模复杂，分析计算量大；悬链线法计算结果精确，但对于多档索道、多载荷等复杂工况的计算欠缺。另外，目前对多承载索索道的结构计算方法研究较少涉及，缺乏必要的承载能力分析方法方面的研究。

本文以弹性悬链线方程为基础，提出一种适用于具有任意载荷的双、四承载索货运索道计算方法，该方法建立了多承载索间、承载索与牵引索间的耦合作用关系，真实反映多索货运索道实际受力状况，可准确分析具有荷载时承载索间的张力变化情况及牵引索对承载索的作用影响，具有计算精度高、效率快、工况适应性强等优点。最后对该方法进行了验证，并开展了多工况计算，为多索索道的设计及安全运行提供理论依据。

1 多承载索货运索道计算方法

1.1 多承载索货运索道结构型式

货运索道主要包括承载索、牵引索、支架(横梁、鞍座)、运行小车、索道牵引装置等。多索索道主要采用多根(2根或4根)钢丝绳同时使用作为承载索，以分担货物重量，实现大型、重型货物的运输。牵引索的作用是牵引运行小车沿承载索运行。如图1所示。

1.承载索；2.牵引索；3.运行小车。图1 工作索耦合系统Fig.1 Coupling system of working ropes

根据货运索道的运行特点，对承载索、牵引索及运行小车提出以下设定：

1)承载索、牵引索在运动过程中始终处于与地面相竖直的平面内。

2)运行小车(及重物)行进时不发生前后扭动。

1.2 货运索道结构分析参数

设多档索道的档数为n，各档跨距为Lsi，高差为hsi，i=1,,n。

承载索、牵引索被载荷点及支架点分为n+m个悬链线索段(各段上仅有重力作用)，编号为1,2,,n+m。记各段工作索起始点为A，终点为B。为便于分析，记各索段中B点为支架点的索段编号为k1,k2,,kn，另补充定义k0=0。记各索段中B点为载荷点的索段编号为g1,g2,,gm，另补充定义g0=0。

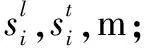
1.3 货运索道索段计算公式

对于承载索与牵引索的第i段(起始点为A，末端点为B)，当已知初始索长、水平张力、A点垂直张力时，根据文献[8]可以得到该段的跨距及高差：

(1)

各段的点A，B的切向张力为：

(2)

各式中增加上标l和t可分别表示承载索张力及牵引索。

1.4 索道结构守恒及平衡方程

在多索索道的计算分析中，需要考虑承载索、牵引索与载荷之间互相耦合作用，在此以四索索道为例，从结构守恒及力平衡等方面建立相应的状态方程。

1.4.1 结构守恒方程

1)档内跨距及高差守恒

每档内各索段的高差、跨距之和等于每档两端的高差、跨距。在此以牵引索为基准，可以列出2n个跨距、高差的守恒公式：

(3)

2)各索段内的跨距及高差守恒

对于多索索道，运行小车不发生前后扭转，因此承载索段与牵引索段的跨距相等；但由于运行小车在垂直方向的偏转，承载索段与牵引索段的高差并不相等，如图2所示。

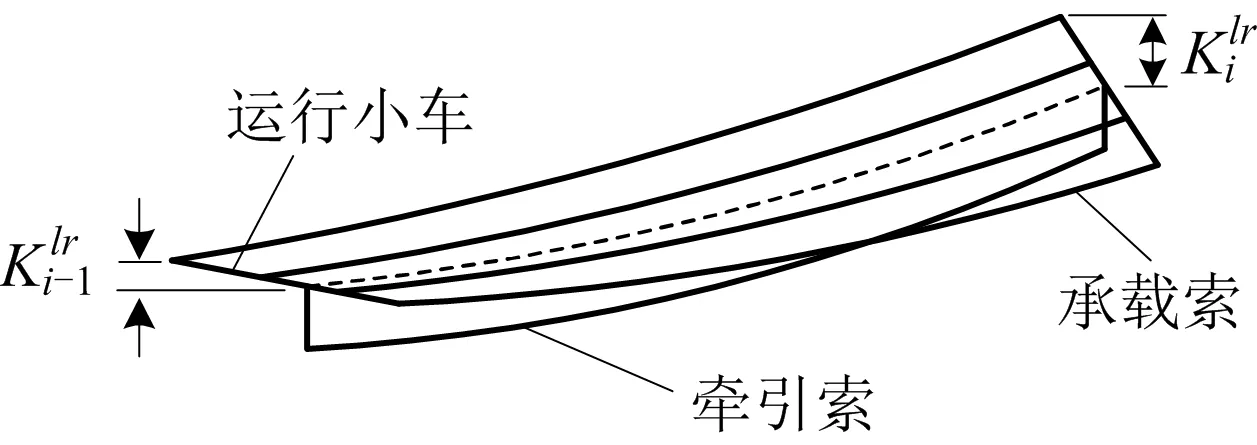
图2 承载索与牵索各段跨距及高差Fig.2 Span distance and height difference of each section between carrying ropes and hauling rope

根据承载索段与牵引索段起始点与终点的相对位置建立方程：

(4)

式中：Klr为承载索相对牵引索的垂直偏转距离，在支架处偏转距离为0，在运行小车处偏转量为Dlrsinωi(ωi为小车偏转角度)。对于四索索道共8(n+m)个方程。

3)牵引索长度守恒

(5)

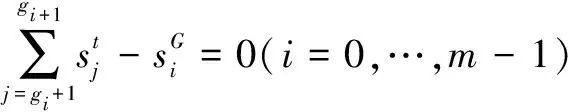
(6)

(7)

1.4.2 力平衡方程

1)支架两侧牵引索张力平衡

牵引索在鞍座的滚轮上移动，摩擦造成的滚轮对牵引索作用力可忽略不计，因此在支架两侧的牵引索切向张力T相等。除起始端和末端的支架外，共有n-1个支架两侧的牵引索切向张力平衡，共n-1个方程：

(8)

2)载荷两侧承载索与牵引索张力平衡

承载索与牵引索在索道档中通过载荷(运行小车)连接，如图3所示。设载荷两侧承载索与牵引索的编号为i及i+1。

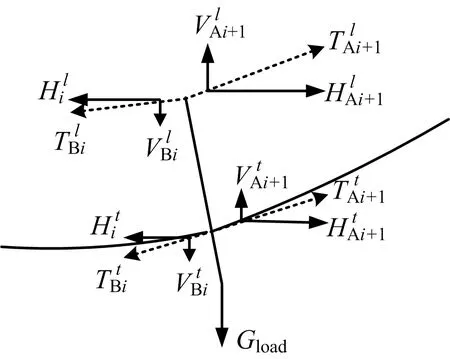
图3 运行小车受力分析Fig.3 Force analysis of running car

运行小车的滚轮对承载索并无轴向力的作用。因此承载索在载荷两侧的切向张力相等，可建立4m个方程：

(9)

运行小车受承载索切向张力、两侧牵引索切向张力、载荷重力共同作用，如图3所示。将各切向张力在水平方向及垂直方向进行分解，可以建立2m个张力平衡方程：

(10)

3)小车在承载索、牵引索、载荷作用下的力矩平衡

造成运行小车偏转的作用力包括承载索对小车的作用力Nlr、牵引索对小车的作用力Nt及载荷Gload，其作用位置如图4所示。

图4 运行小车受力示意Fig.4 Force schematic diagram of running car

设运行小车的偏转角度为ω，以运行小车中心O为中点，可建立小车在承载索、牵引索、载荷作用下的m个力矩平衡方程：

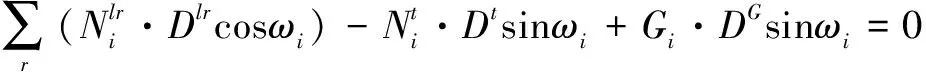
(11)

1.4.3 索道整体非线性方程组

根据结构守恒方程和力平衡方程可以建立各类条件对应的非线性方程组，方程数目与未知数个数相等，因此方程组闭合。可以将其表示为：

F(X)=0

(12)

该方程组可采用牛顿迭代法求解[9]，进而获得承载索张力等结果。

1.5 算法验证

为对本文计算方法的有效性进行验证，依托国家电网公司某500 kV输电线路工程，开展四索2档货运索道现场试验，具体四索索道示意如图5所示。试验索道第1档跨距248.6 m，高差114.5 m；第2档跨距49.9 m，高差16.9 m。试验索道选用的承载索直径30 mm，单位长度质量3.42 kg/m；牵引索直径26 mm，单位长度质量2.57 kg/m；钢丝绳弹性模量90 GPa。

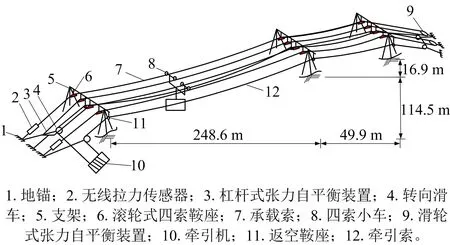
图5 四索索道示意Fig.5 Schematic diagram of ropeway with four ropes

选取5.5 t试验载荷工况，采用本文提出的计算方法进行计算，将得到的承载索1和承载索2张力计算值与试验测量值作对比，如图6和图7所示。承载索1和承载索2分别对应无线拉力传感器1和2。

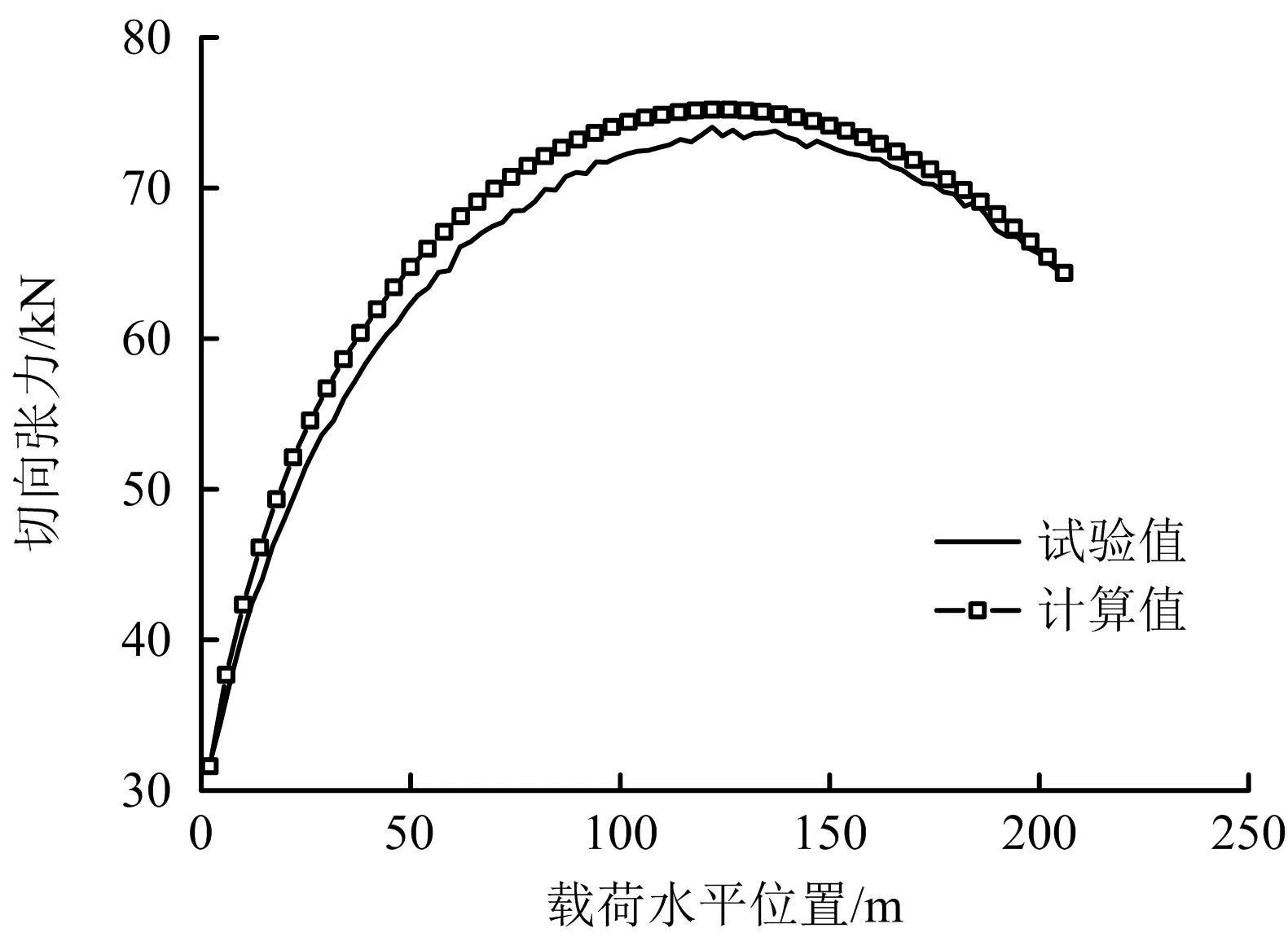
图6 承载索1切向力计算与试验值对比Fig.6 Comparison between calculated values and test values of tangential force for carrying rope 1

图7 承载索2切向力计算与试验值对比Fig.7 Comparison between calculated values and test values of tangential force for carrying rope 2

由图6和图7可知，计算结果与试验测量值的变化趋势一致。具体而言，承载索1最大张力试验值为74.23 kN，计算值为75.20 kN，与试验值的相对误差为1.3%；承载索2最大张力试验值为81.50 kN，计算值为83.20 kN，与试验值的相对误差为2.1%；计算结果的相对误差均很小，满足工程应用需求。试验值均比计算值略小，主要是由于钢丝绳捻制工艺导致其受力后发生一定的结构性伸长，使得钢丝绳实际弹性模量发生微小变化，从而造成计算值略大于试验测量值。

2 多承载索货运索道不平衡效应分析

对于多承载索货运索道，在施工过程中钢丝绳不可避免的产生蠕变伸长[10]，且由于安装、钢丝绳自身结构等因素的影响，不同钢丝绳的蠕变伸长量并不相同，因此造成各承载索间长度产生偏差。该偏差对承载索的张力影响较大，是评价多索索道安全性能的重要指标。

在此，以四承载索货运索道的典型工况，计算分析承载索间的耦合作用影响。为有效衡量分析工况对不平衡效应的影响程度，定义索间张力不平衡系数：

(13)

式中：λ为张力不平衡系数；Tr为承载索不等长时各索的最大切向张力，kN；T0为承载索等长时各索的最大切向张力，kN。

2.1 索道主要参数

结合工程中典型工况，设定四索索道档间高差为50 m，跨距为300 m。承载索直径26 mm，弹性模量110 GPa，单位长度质量2.57 kg/m，承载索基准长度为306 m；牵引索直径24 mm，弹性模量100 GPa，单位长度质量2.19 kg/m，牵引索长为308 m，载荷重量为10 t。

2.2 索长不平衡工况分析

因四承载索索道的索1,2与索3,4位置对称，以下仅针对索3,4分析不同长度变化工况时各索的最大承载张力值变化情况。

1)工况1：索1,2,4为306 m，索3从306 m伸长至307 m。其中， 各索张力随索3长度变化曲线如图8所示。

图8 各索张力随索3长度变化Fig.8 Variation of tension of each rope with length of rope 3

从图8可以看出，由于索3长度伸长，载荷主要由索1，2，4承担，索4的不平衡系数最大，达到38.69%；而索3的张力迅速减小，当长度增加1 m时，，索3张力仅有28.22 kN。可见，当四索索道中间承载索长度伸长时，会导致其余3根承载索张力同时增大，增幅最大的是靠近伸长承载索的外侧索。

2)工况2：索1，2，3为306 m，索4从306 m伸长至307 m。其中，各索张力随索4长度变化曲线如图9所示。

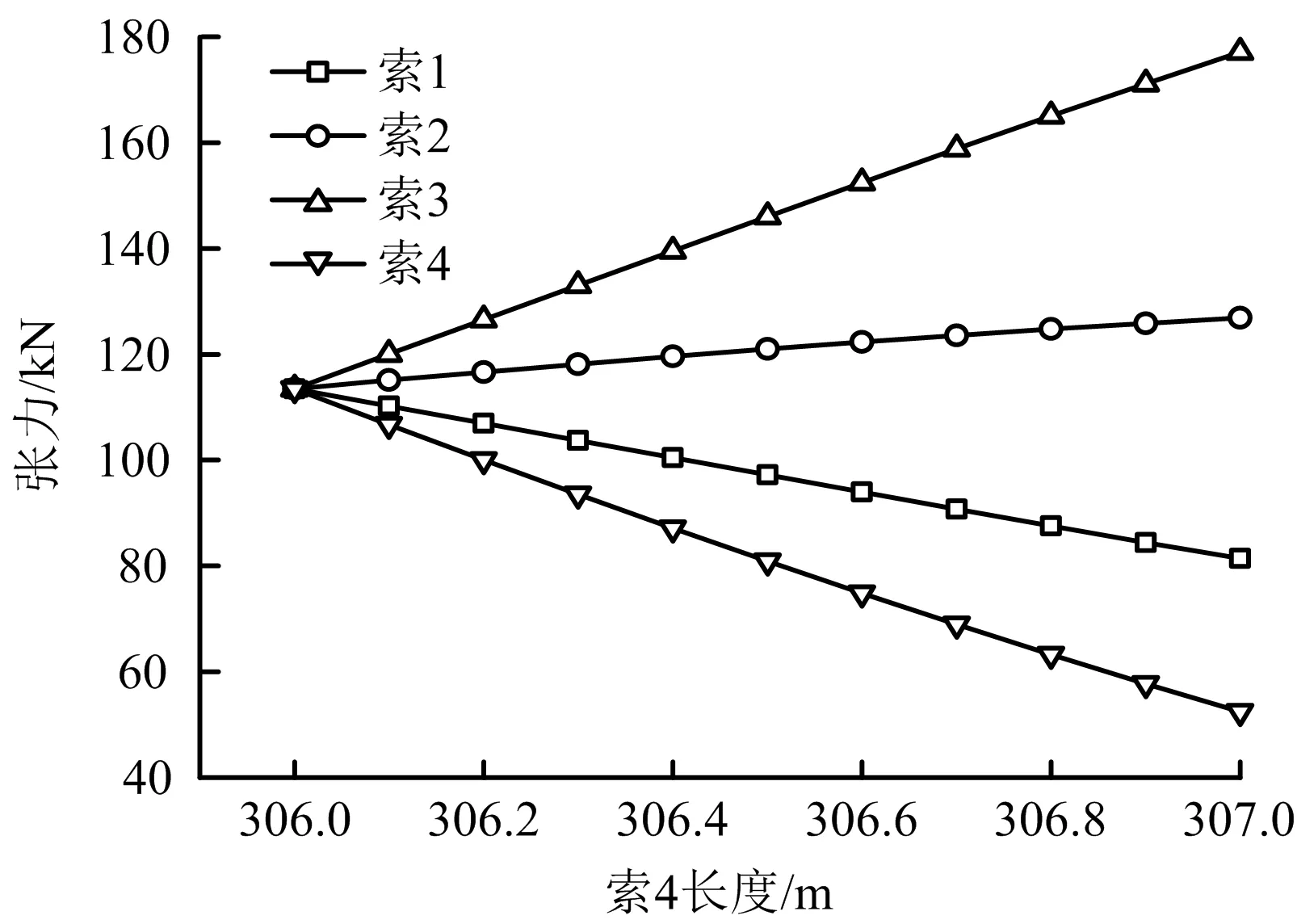
图9 各索张力随索4长度变化Fig.9 Variation of tension of each rope with length of rope 4

从图9可以看出，随着索4长度的伸长，索4和索1的张力逐渐减小；索2和索3的张力逐渐增大，索3的张力不平衡系数最大，达到56.04%。可见，当四索索道外侧索伸长时，会导致靠近伸长承载索的内侧索张力急剧增大。

3)工况3：索3为306 m，索1，2，4从306 m同时伸长至307 m。其中，各索张力随索1，2，4长度变化曲线如图10所示。

图10 各索张力随索1，2，4长度变化Fig.10 Variation of tension of each rope with length of rope 1, 2 and 4

从图10可以看出，由于索1，2，4同时伸长，载荷主要由索3承担，其张力不平衡系数最大达到117.90%，张力增加了133.82 kN，其他承载索张力均迅速减小。可见，四索索道中内侧索较短极易造成该承载索的破断，进而影响其他承载索，将会对索道的运行安全造成极大的影响。

4)工况4：索4为306 m，索1，2，3从306 m同时伸长至307 m。其中，各索张力随索1，2，3长度变化曲线如图11所示。

图11 各索张力随索1，2，3长度变化Fig.11 Variation of tension of each rope with length of rope 1, 2 and 3

从图11可以看出，随着索1，2，3的同时伸长，索4和索1的张力逐渐增大，索2和索3的张力逐渐减小。其中，索4张力变化最大，不平衡系数达到64.94%。可见，当四索索道外侧索较短时，会造成两侧外侧索张力同时增大。

以上4种工况各工况承载索伸长变化与张力变化最大索情况如表1所示。

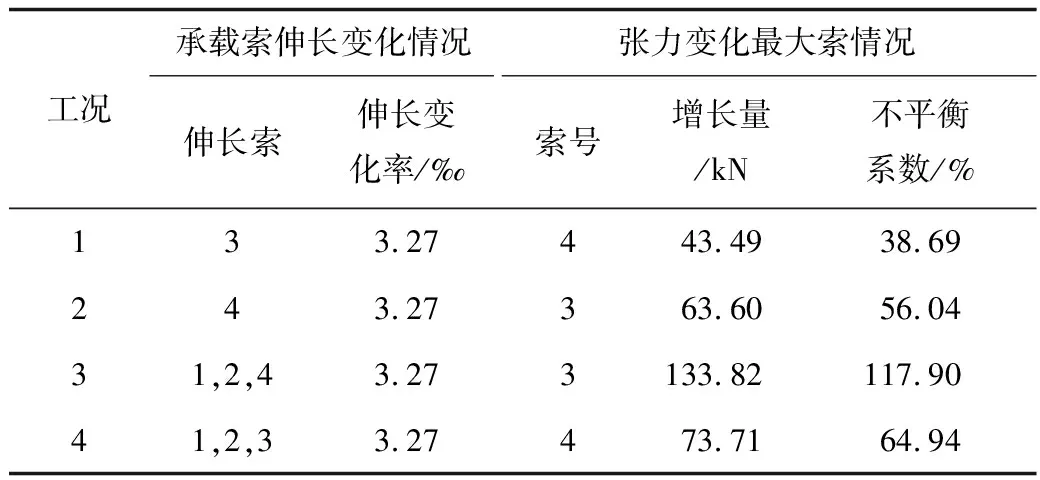
表1 长度变化与不平衡系数Table 1 Length variation and unbalance coefficient

2.3 载荷重量变化工况分析

根据前文分析可知，当四索索道内侧索较短时，张力不平衡效应最大。在此分析载荷重量变化对多承载索不平衡系数的影响情况。采用索3长度为306 m，索1，2，4长度均为307 m，载荷重量分别为2，4，6，8和10 t。其中，各索张力随载荷重量变化曲线如图12所示。

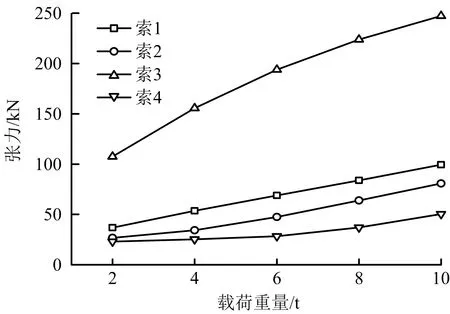
图12 各索张力随载荷重量变化Fig.12 Variation of tension of each rope with load weight

从图12可以看出，各索张力随载荷重量增大而逐渐升高，索3由于长度较短，其张力远远大于其余3根索的张力。对索3进行张力不平衡系数计算分析，索3张力不平衡系数随着载荷重量增大逐渐下降，说明载荷重量小对承载索的张力不平衡影响较大。如载荷重量为2t时，索3的不平衡系数达到164.16%。

3 结论

1)本文提出的多承载索货运索道整体系统耦合动力计算方法简洁、形式统一，易于程序实现，适用于双索、四索的多索索道整体结构的精确计算，为重型货运索道的设计提供理论方法。

2)多承载索货运索道各承载索间长度的偏差对承载索的张力影响极大，且影响程度与索长变化工况相关。对于四承载索索道，当内侧索较短时该承载索的张力不平衡系数最大，如本文分析的典型工况中其不平衡系数达到117.90%，此种工况极易造成承载索破断而引起索道安全事故的发生。

3)对于索长不平衡的多索货运索道，其张力不平衡系数受载荷重量影响较大。随着载荷重量增加，不平衡系数逐渐下降。

4)在现场施工时，应及时调整多索索道的承载索长度，减少索长间的不平衡性；另可设计张力自平衡装置，在索道运输过程中，依靠多承载索间的张力变化，自动调整各承载索长度，避免张力不平衡效应的出现。