基于坐标变换的三相逆变并网控制策略

邓孝祥，张家琪

（黑龙江科技大学 电气与控制工程学院，黑龙江 哈尔滨 150022）

0 引 言

当今世界对新能源的使用和研究日益增多，其中并网逆变器作为新型能源与电网连接备受关注。并网逆变器通常采用SPWM脉宽调制技术，通过逆变电路开关器件的通断，得到一系列幅值相同的脉冲，这些脉冲与电网同频同幅同相位。但是，SPWM脉宽调制技术仅仅做到了波形变化的同步，同时会向电网输送杂波。谐波可引起系统的电感、电容发生谐振从而放大谐波。因此，研究并网逆变器的控制策略具有重要的理论意义和实用价值。文献[1]提出了最大功率点跟踪技术，通过SPWM脉宽调制技术实现并网，但易产生进网谐波，且电压利用率不高。文献[2]提出了PI控制，提高了系统稳定性，但采用了SPWM脉宽调制技术。文献[3]采用双极性SPWM控制策略，通过双闭环控制系统进行控制。文献[4]介绍了dq轴解耦技术，但未在扇区选择详细说明。文献[5]介绍了光伏并网的控制策略，但未构建数学模型加以解释。本文提出了一种基于坐标变换的空间矢量脉宽调制控制策略，通过控制三相逆变器的IGBT开关的开通与关断的顺序与时间，采用电压矢量合成法实现SVPWM，利用Matlab/Simulink仿真平台验证了该控制策略对抑制谐波和提高入网电压质量的有效性和可行性。

1 三相并网逆变器的拓扑结构

三相全桥式并网逆变器主电路的拓扑结构如图1所示，左侧三相电网电源分别为Uga、Ugb以及Ugc，电路中逆变器所产生的输出电流分别为ia、ib与ic，而进入电网的入网电流分别为iga、igb与igc。S1～S6为IGBT功率器件，Udc为直流侧电压。

图1 主电路拓扑结构

由图1可列出在abc三相静止坐标轴中三相电流与电压的状态方程：

2 坐标轴变换数学模型

由于三相并网逆变时的变量多为交流量，不便于更深入的研究，也不利于计算，故采用坐标轴变换的方法将交流量变为直流量，以减少变量，简化计算。坐标轴变换分为Clark变换和Park变换。Clark变换如图2所示。一般将三相静止坐标轴的a轴与两相静止坐标轴的α轴相重合。

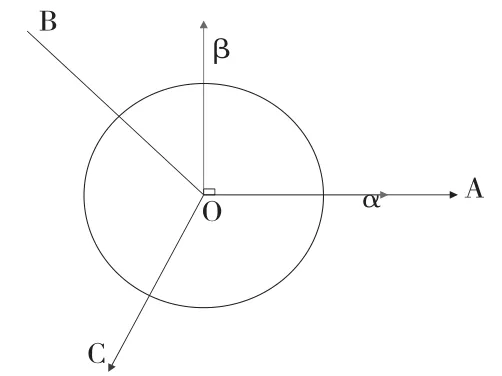
图2 Clark变换

在三相静止坐标轴和两相静止坐标轴的基本坐标轴相重合时，可以得出其矩阵变换公式如下：

式（1）、式（2）和式（3）经过计算得到dq两相旋转坐标轴下的电流与电压的状态方程：

为了将三相交流的变量转化为两相直流的量，需要进行如图3所示的Park变换即2s/2r坐标轴变换，其中取旋转坐标轴的旋转角速度为三相电网电压的频率。

图3 Park变换

变换后可得矩阵：

两相静止坐标轴和两相旋转坐标轴下的入网的电流状态方程关系如下：

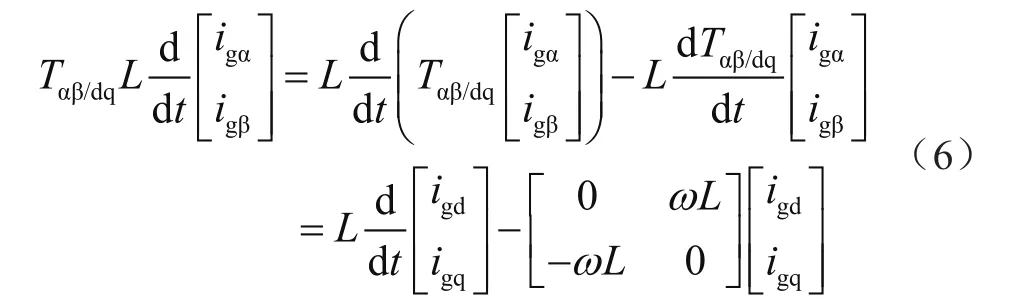
联立式（4）、式（5）和式（6）可以得到dq两相坐标轴下逆变器的状态方程组：

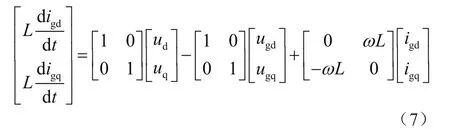
式（7）表明：通过3s/2s变换和2s/2r变换可以得到三相并网逆变器在两相旋转坐标轴下的状态方程，将d轴电流与q轴电流解耦合分离，即可控制进网的无功功率和有功功率。

3 空间矢量控制策略

3.1 SVPWM控制原理

SVPWM空间矢量脉宽调制类似于同步型电机中三相电源的三相逆变器的IGBT开关的开通与关断的顺序与时间，通过一系列开关的导通关断形成的电流波形相位之间相互差别120°。三相电压的abc三相电压合成的电压值：

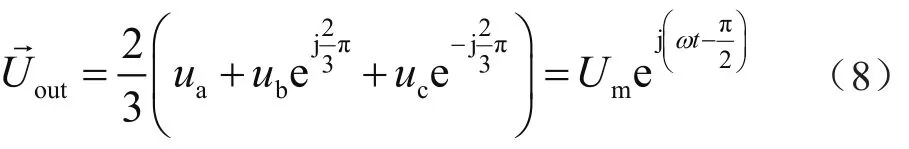
三相并网逆变桥的6个功率器件的开通和关断有不同的组合状态，排列组合后可得8种IGBT导通状态的组合形式，即可以表示为8种空间矢量。（0，0，0）与（1，1，1）属于无电压型空间矢量，剩余还有6种不同组合的有值电压型空间矢量，绘制成空间矢量图如图4所示。V0与V7是两个零电压基本空间矢量，其余6个为非零型电压基本空间矢量。

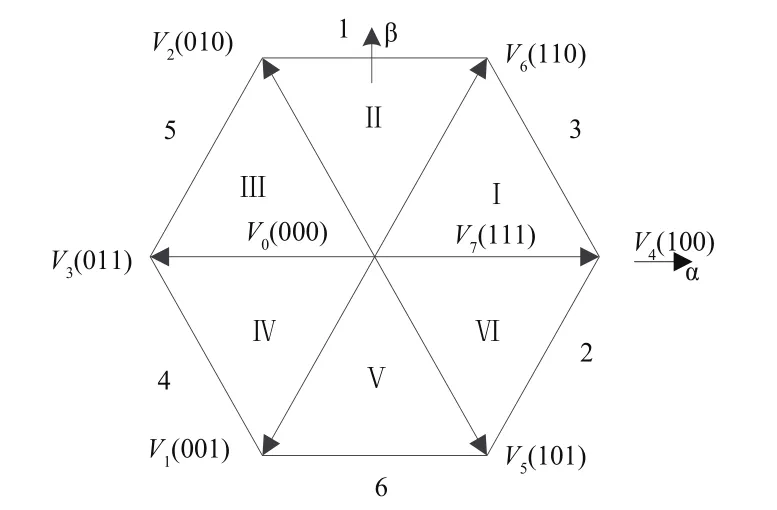
图4 8种基本电压空间矢量组成的矢量图

本文采用电压矢量合成法实现SVPWM，由6个区域中相邻的两个有值矢量与无值矢量的不同作用时间相合成电压空间矢量，取有值矢量作用时间为TK，无值矢量作用时间为T0，根据SVPWM原理可以得到：

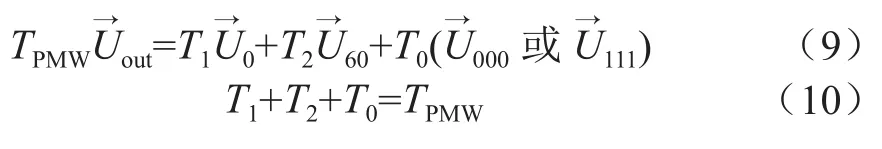
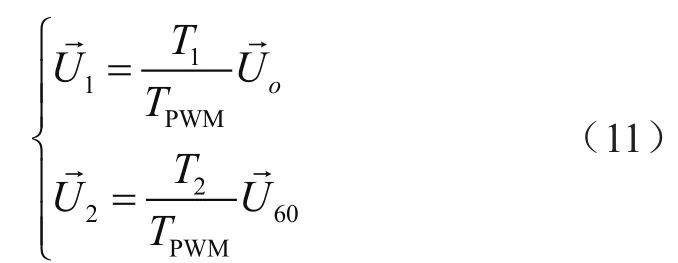
在判断基本空间矢量所在扇区时，先构造出3种不同的变量——Vref1、Vref2、Vref3。用这3种变量的正负来判断所对应的扇区，公式如下：

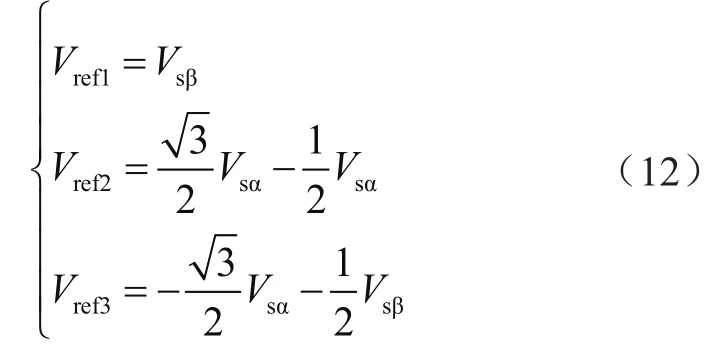
定义二值函数A、B、C，若Vref1＞0，则A=1，反之A=0；若Vref2＞0，则B=1，反之B=0；Vref3＞0，则C=1，反之C=0。

由式（13）可得不同的取值，即可对应不同的扇区。在得到不同扇区空间矢量的判断后，还需要计算空间矢量作用的时间T0、T1与T2。

通过图5空间矢量合成图可得：

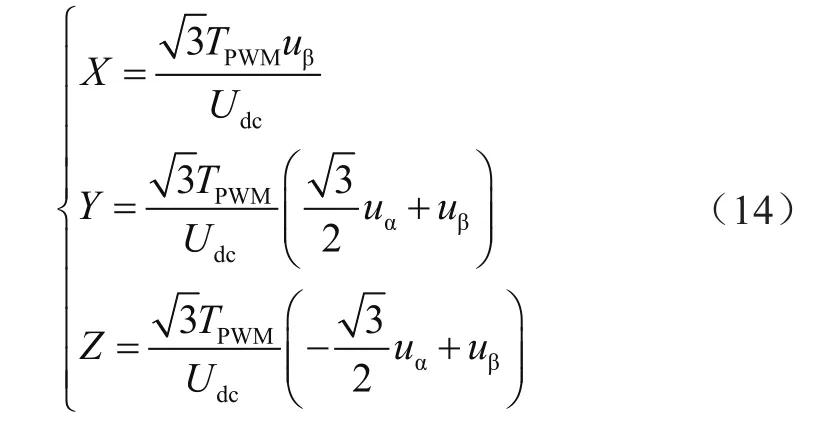
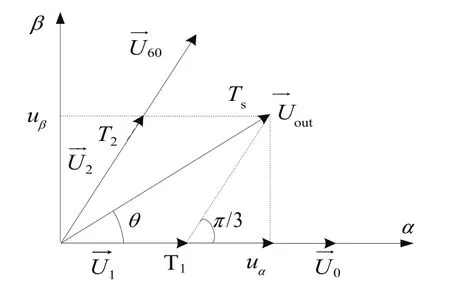
图5 电压空间矢量合成示意图

由式（14）能够得到6个空间扇区T1、T2、T0作用的时间，如表1所示。其中，N代表空间扇区，X、Y、Z分别为各扇区作用时间分量。

表1 各扇区T1、T2、T0作用时间

假设零矢量在一个开关周期中作用时间相同，每个基本空间矢量分别作用对称的时间，将三角波周期TPWM作为定时周期，得出如图6所示的SVPWM波形。

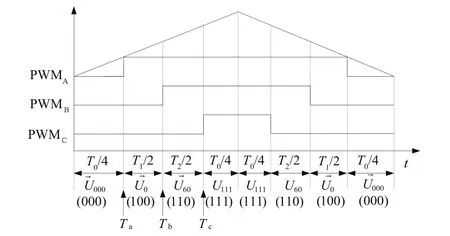
图6 扇区I内三相SVPWM调制方式

3.2 dq坐标轴下的解耦控制

通过计算可以得出在dq坐标轴下三相电网的有功功率P与三相电网的无功功率Q的公式：

在旋转坐标轴下，只需控制dq轴上的直流电流即可控制进网功率，但需要对dq轴分量解耦计算。

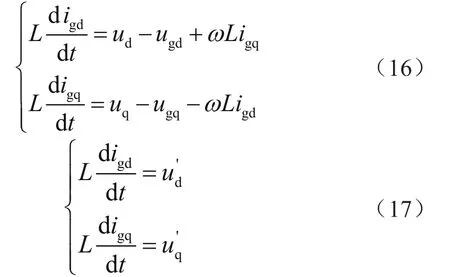
其中与是可以控制的两个变量，此时经过解耦的电流id与iq为独立量，即可得：

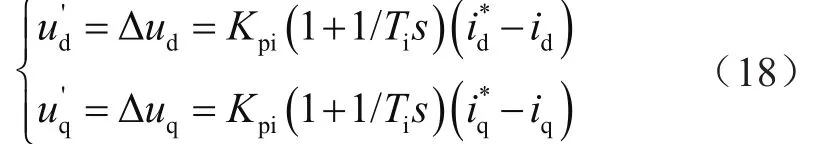
式中Δud，Δuq是在dq旋转坐标轴下PI调节输出值，Kpi是PI调节输出的比例环节系数值，Ti为积分环节中的时间系数值，和是dq两相旋转坐标轴的参考电流值。根据上述得到最后的电压控制方程为：

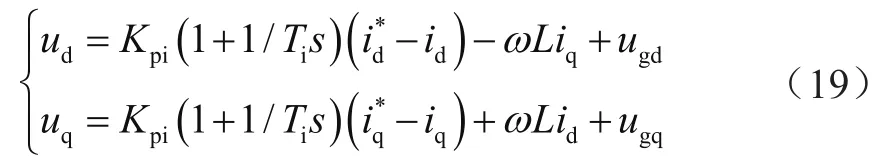
式（19）易看出dq坐标系下的两相电流已经解耦，能够相互独立被控制，同时还将三相电网中的id与iq值作为该调节的前端反馈，能够更加稳定地控制电网并网。

4 仿真结果与分析

在MATLAB/Simulink仿真软件上设计搭建了基于旋转坐标系的三相并网逆变器控制策略的仿真模型，其中仿真参数设置如下：直流电压Udc=550 V，TPWM=0.000 1 s，给定三相参考相电压有效值220 V，电网频率为50 Hz，额定功率为50 kVA，仿真时长设置参数为50e-6 s。

由图7可以看出，在0.1 s仿真周期中，电网电压与进网电流波形同频同相位。继而对SVPWM调制方法进行仿真后得到三相调制波波形。

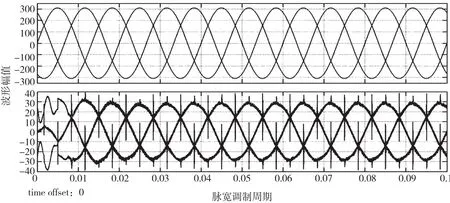
图7 三相并网逆变器系统仿真图

由图8可以看出，由SVPWM算法得到的调制波呈马鞍形，相对于PWM得到的正弦波来说，有利于提高直流电压利用率，能够有效抑制谐波。

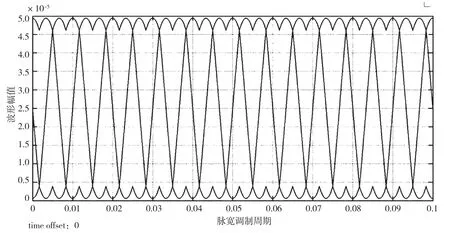
图8 SVPWM调制波波形图

5 结 论

本文针对SPWM脉宽调制技术在三相并网逆变器中易产生谐波、电压利用率低的问题，提出了SVPWM空间适量调制技术，构建了在旋转坐标系下三相并网逆变器模型结构，同时解释了在dq两相旋转坐标系下的直流量解耦合技术，证明了SVPWM能够更好地优化进网谐波，提高电压利用率。在Matlab/Simulink中搭建仿真模型，验证了设计的原理及控制方法的正确性与可行性。