高速铁路连续梁桥横向地震碰撞效应及挡块间隙研究
,2
(1.中南大学土木工程学院,湖南长沙,410075;2.上海市政工程设计研究总院(集团)有限公司,上海,200092)
高速铁路是国家经济大动脉、重大公共基础设施和生命线工程,而桥梁在高铁线路中占有较大比例[1],且越来越多的高速铁路桥梁修建于地震区,如何提高高铁桥梁的抗震性能是高速铁路建设中亟待解决的问题。为了避免横桥向落梁等灾难性损坏,高铁桥梁通常在梁底横桥向设置型钢挡块等限位装置。在强震作用下,桥梁上下部结构由于动力特性不同发生不同相振动,若墩梁横向相对位移超过挡块-垫石间距,则会引起挡块与垫石间的非线性横向碰撞。碰撞不但可能会造成桥梁限位装置自身损坏,而且会引起下部结构内力增大,增加桥墩延性变形能力需求。国内外一些学者对地震作用下桥梁横向碰撞效应进行了研究,如:MALEKI等[2]认为在横桥向地震反应中,挡块与梁体间的作用关系本质上是非线性的,且挡块与梁体间的初始间隙是对横向碰撞效应产生重要影响的因素;邓育林等[3]提出最大碰撞力随碰撞刚度和桥梁跨径增大而增大,忽略碰撞过程中的能量损失会高估碰撞反应。王军文等[4]以1座非规则连续梁桥为例,探讨了减轻横向碰撞和限制相对位移的措施和方法;DIMITRAKOPOULOS等[5]建立了可用于研究分析斜桥地震碰撞反应的新型非光滑刚体模型,指出分析计算时应考虑上部结构偏心、墩柱线刚度及支座动力特性和桩-土作用等的影响;徐略勤等[6]通过考虑上部梁体与挡块间的横向碰撞效应,研究其对非规则梁桥横向地震反应的影响,并指出碰撞会使桥梁结构动力响应加大,造成各墩受力重新趋于不均匀;石岩等[7]发现高铁简支梁桥挡块与垫石间的碰撞实际上是大偏心碰撞且可能引起桥墩破坏,在其间设置硬木垫块可以降低碰撞力,提高高铁桥梁横向抗震性能;贾宏宇等[8]基于高墩铁路桥梁研究了不同震级不同场地分布对桥梁碰撞间隙宽度需求的影响规律;吴刚等[9]研究指出挡块力学性能退化对横桥向地震响应影响较大,在中小跨径梁桥抗震分析中应予以考虑。可见,人们对已有横向碰撞效应的研究多集中于公路桥梁[2-6],而对铁路桥梁碰撞研究较少,且多忽略桥面系的影响[7-10],而考虑轨道系统影响的研究也仅限于简支梁桥[11-12],针对高速铁路连续梁桥横向碰撞效应的研究较少。为此,本文作者以(2×32 m简支梁+(48+80+48)m连续梁+2×32 m简支梁)高速铁路简支-连续组合桥梁为例,采用ANSYS有限元软件建立轨道系统—梁体—桥墩一体化模型,分析轨道系统约束作用和横向限位挡块对横向地震响应的影响,并探讨挡块-垫石间距(加设橡胶缓冲装置)对桥梁横向地震碰撞效应的影响。
1 高铁连续梁横向碰撞有限元模型
1.1 研究对象
将常见的高速铁路2×32 m简支梁及(48+80+48)m连续梁的组合桥梁作为研究对象,整体桥跨布置如图1(a)所示,全桥挡块编号如图1(b)所示,且桥台未设置挡块。主梁均为双线单箱单室截面,材料为C50混凝土,桥面宽为12.600 m。连续梁中支点箱梁中心线梁高为6.635 m,跨中及边支点箱梁中心线梁高为3.835 m,梁底线形按二次抛物线变化,简支梁箱梁中心线梁高为3.035 m。轨道结构采用我国现有纵连板式无砟轨道预制轨道板(CRTSⅡ型),由滑动层、底座板、CA砂浆层、轨道板、L型侧向挡块、扣件和钢轨等构件组成,轨道系统及挡块构造如图2所示。支座选用高铁桥梁中广泛采用的TJQZ型球形钢支座,其中简支梁为TJQZ5000型球形钢支座,连续梁边墩采用TJQZ7000型支座,中墩采用TJQZ35000型球形钢支座。每跨4个支座且每侧横桥向均有1个横向固定和横向可滑动支座。桥墩为圆端型实体墩,墩高均为10.000 m,材料为C35混凝土,基础采用钻孔灌注桩基础。
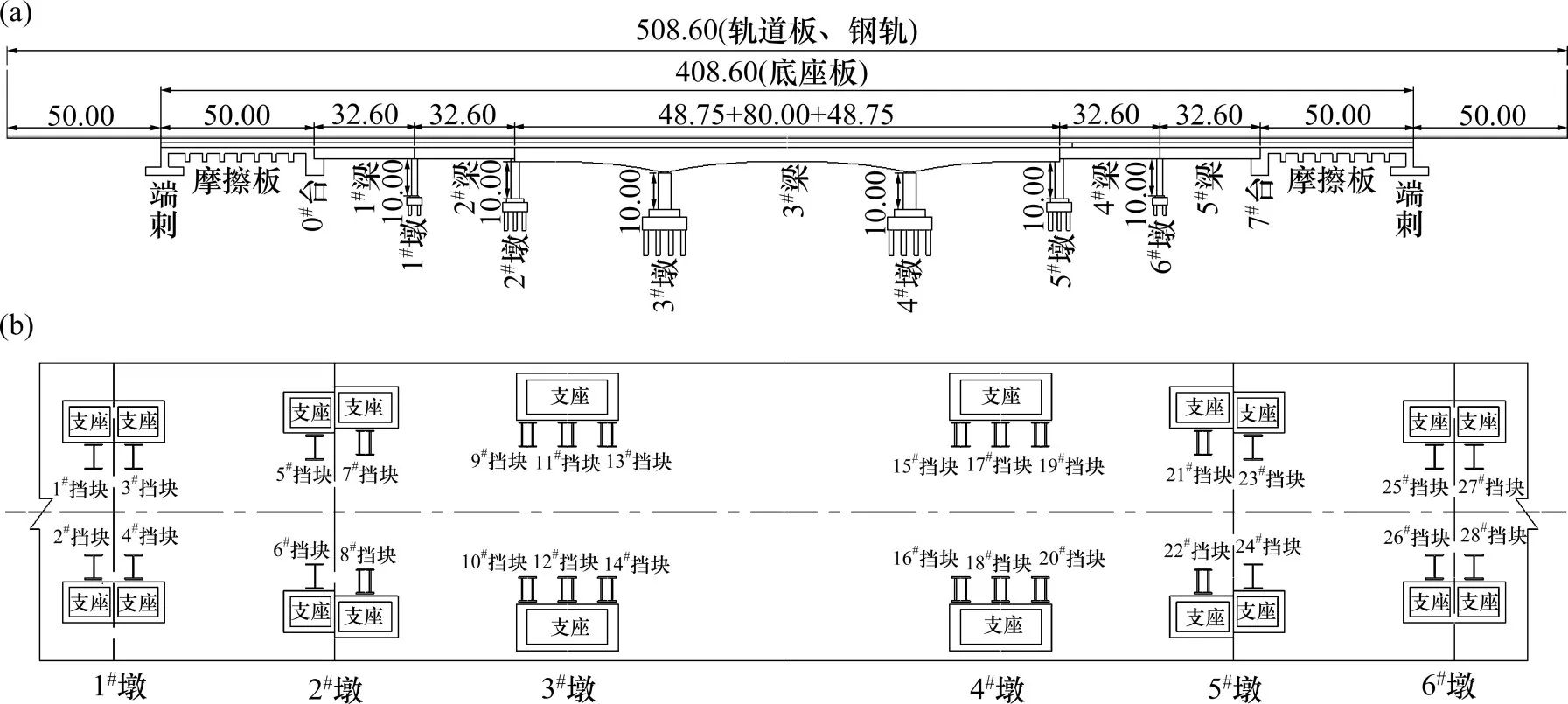
图1 桥型布置图及挡块编号Fig.1 Elevation of bridge and numbers of shear keys

图2 轨道系统及挡块构造图Fig.2 Sketch of track system and shear keys
1.2 有限元建模及取值

图3 全桥有限元模型Fig.3 Finite element model of bridge

图4 轨道系统有限元模型Fig.4 Finite element model of track system
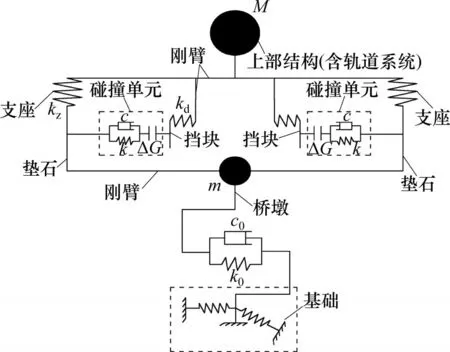
图5 高铁桥梁横向碰撞体系示意图Fig.5 Transverse pounding model sketch of bridge
采用ANSYS有限元软件建立高铁桥梁横向碰撞杆系有限元模型,其中全桥有限元模型和轨道系统局部有限元模型分别如图3和图4所示,横向碰撞体系示意见图5。桥梁两端各模拟100 m路基作为钢轨锁定点[12-13],路基两侧纵向各取50 m的摩擦板。主梁及轨道结构采用线性梁单元模拟,因桥面系横向设有侧向挡块,故不考虑底座板的滑动,认为其与梁体固结。线路扣件横向阻力采用试验拟合结果[14],模型中采用非线性弹簧单元combin39模拟。台后传力锚固体系中的摩擦板以及路基轨道结构中的HGT水泥硬化支撑层均视为与大地固结。桥墩混凝土取用Mander材料本构模型并假设塑性铰发生于墩底,墩底截面的弯矩-曲率即M-φ曲线采用UCFyber软件计算得到,各桥墩等效塑性铰长度依据“公路桥梁抗震设计细则”[15]计算确定。桥墩潜在塑性铰区采用弹簧单元combin40来体现其塑性回转能力,其余部分采用线性梁单元模拟,桥台采取固结方式处理。使用等效的平动和转动弹簧模拟桩土共同作用。活动支座滞回模型类似于理想弹-塑性模型,摩擦因数取0.03[12],有限元模型中采用弹簧单元combin39模拟。固定支座破坏前恢复力模型近似为理想刚塑性,水平向最大承载力Fmax与桥址烈度(设防烈度为7度)有关,简支梁固定支座抗力为竖向承载力的22.5%,连续梁边、中墩横向固定支座抗力为竖向承载力的30%。固定支座被剪坏后,其纵向阻力近似于滑动摩檫力。固定支座采用combin40单元模拟支座剪坏前的力学特性,同时并联combin39单元模拟支座剪坏后的滑动摩擦状态。支座恢复力模型如图6所示,其中,Fcr为临界摩擦力,x为支座顶面和底面的相对水平位移,xy为滑动临界位移,k为滑动刚度。
1.3 挡块-垫石碰撞模拟

图6 支座力与位移关系曲线Fig.6 Force-displacement curves of bearings

图7 钢挡块力与位移关系曲线Fig.7 Force-displacement curve of shear key
选用的通用桥梁限位挡块适用于抗震设防烈度为7度地区。汤振辉等[16-18]对桥梁钢挡块进行了大量试验研究与数值仿真,结果均表明钢挡块具有较明确的力学性能,其力-位移关系可用双线性单元模拟,如图7所示(其中,Fy为钢挡块的屈服荷载,Ke和Ku分别为钢挡块的弹性刚度和屈后刚度,dy为屈服位移)。为了得到挡块力与变形曲线的真实值,本文还建立了挡块实体有限元模型,将其底部固结,并假设在地震作用下,碰撞发生在挡块与垫石接触面的中心线位置,在该中心线范围内逐级加载,得到该挡块的力与变形曲线,并将其等效为双折线,以体现挡块在受力情况下的非线性行为。挡块力学特性如表1所示。
高铁简支梁和连续梁支座垫石通常分别采用C40和C50混凝土,且配筋率较高,本文不考虑垫石混凝土进入塑性阶段,有限元模型中采用线性梁单元模拟。简支梁挡块-垫石间距取3 cm,连续梁取2 cm。

表1 挡块力学特性Table1 Mechanical properties of shear keys
在地震作用下,挡块垫石间的碰撞现象采用Kelvin模型进行模拟,在有限元模型中采用弹簧单元combine40来实现,其非线性力-位移关系为

式中:k为碰撞刚度,根据表1取值;d为地震作用下挡块与垫石间的横向相对位移;ΔG为挡块垫石初始间隙;v为碰撞体系相对速度;c为碰撞过程中的阻尼系数,与碰撞过程中的恢复系数e有关(混凝土材料e取0.65)。阻尼系数c的计算公式[19]为

式中:M为上部结构质量;m为下部结构质量。关于碰撞中接触阻尼的模拟,应分别将挡块弹性和屈后刚度代入式(2)计算阻尼系数。有限元中借助2个并联的combine37单元实现各阻尼在对应阶段发挥作用。
2 横向地震碰撞效应
时程分析采用Rayleigh阻尼,阻尼比ξ取为0.05。选取3条代表性地震波El-Centro,Taft和汶川地震波(对应的卓越频率分别为1.79,2.78和10.00 Hz),地震设防烈度为7度,保留各地震波频谱特性,将各波调幅至PGA(即峰值地震动加速度)为0.32g(罕遇地震后,1g=9.8 m/s2),进行横向非线性时程反应分析。3条地震波的加速度反应谱曲线如图8所示。
2.1 轨道系统对碰撞效应的影响
为分析轨道系统约束作用对高铁桥梁横向地震响应的影响,分别建立有轨和无轨这2种高铁桥梁模型,其中,无轨模型二期恒载通过换算梁体密度来计算其质量。2个模型的横向前6阶模态自振频率见表2,其中有轨模型的横向前6阶振型见图9。通过非线性时程分析得到El-Centro波作用下有轨与无轨最大碰撞响应之比,如图10所示。

图8 3条地震波的加速度反应谱曲线Fig.8 Acceleration responses spectra for three kinds of seismic waves

表2 2种模型横向模态频率对比Table2 Comparison of transverse frequences of two models Hz
由表2可见:轨道系统约束作用会增大桥梁结构的横向刚度,使得结构自振频率增大,进而影响高铁桥梁的横向地震响应。从图10可以看出:一方面,轨道系统减小了墩梁横向相对位移和挡块碰撞力,且越靠近边跨路基,部分轨道约束作用越强,使得简支梁部分甚至不发生碰撞;另一方面,轨道系统放大了墩底剪力(墩顶位移)分配的不均匀性,这主要是因为在轨道及路基的共同作用下,桥梁整体性加强,各墩刚度并联,桥墩承担的横向地震力与各墩刚度成正比,且路基对于边跨简支梁部分的梁段约束作用明显高于中间连续梁部分的梁段的约束作用,由此导致桥墩之间的墩底剪力分配不均匀性更加明显,且向横桥向刚度最大的连续梁中墩集中。

图9 有轨模型横向前6阶振型Fig.9 First six transverse modes of vibration of model considering track system
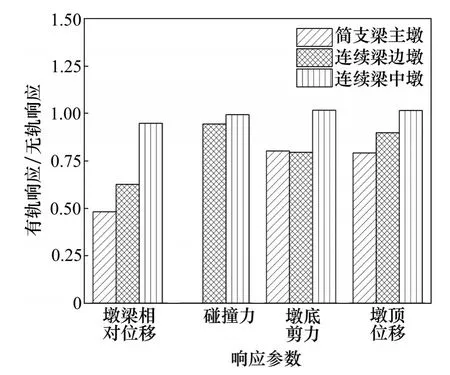
图10 轨道系统对横向碰撞效应的影响Fig.10 Effects of track system on transverse pounding responses
可见,轨道系统对桥梁结构横向动力特性及地震响应均有较大影响。为了更真实地模拟桥梁结构在地震作用下的受力状态,在后续分析中均考虑轨道系统的影响。
2.2 横向限位挡块的影响
为了解设置型钢挡块(未加设橡胶缓冲装置)对横桥向抗震性能的影响,通过非线性时程分析得到El-Centro波作用下横向限位挡块对墩梁横向相对位移、墩底剪力和墩顶位移的影响。这里仅列出连续梁中墩(3号墩)处墩梁横向相对位移、挡块碰撞力时程以及考虑限位与无限位最大碰撞响应之比,如图11所示。
由图11可知:限位挡块可有效降低墩梁横向相对位移,对横向限位防落梁起到重要作用;设置挡块后,由于挡块与垫石在强震作用下发生碰撞,碰撞力通过垫石传递到桥墩,造成墩底剪力和墩顶位移也相应增大。可见,碰撞放大了桥墩的地震需求,可能造成桥墩过早进入塑性或弯曲破坏,这也为在挡块间隙内加设橡胶缓冲装置提出了需求。

图11 横向限位挡块对横向地震响应的影响Fig.11 Effects of the shear keys on transverse pounding responses
3 横向挡块-垫石间距分析
3.1 横向挡块-垫石间距对地震碰撞效应的影响
初始间隙即挡块-垫石间距是碰撞问题中的一个重要参数,高铁连续梁边墩和中墩挡块-垫石间距设计值通常取为2 cm。为研究初始间隙对高铁桥梁横向碰撞效应的影响,分别取1,2,3,4和5 cm共5种挡块-垫石间距,输入El-Centro波、Taft波和汶川波,得到3条地震波作用下墩梁最大横向相对位移、最大碰撞力和墩底最大剪力随挡块-垫石间距变化的情况,其结果如图12所示。

图12 初始间隙对横向碰撞效应的影响Fig.12 Effects of initial gap on transverse pounding responses
由图12可知:墩梁最大横向相对位移基本随挡块-垫石间距的增大而增大,由于在汶川波作用下,连续梁中墩横向固定支座一直未发生破坏,因而,其墩梁最大横向相对位移基本没有变化,这主要与地震波的频谱特性有关。桥梁结构的横向一阶自振频率为2.37 Hz,与El-Centro波和Taft波的卓越频率较接近,而与汶川波的卓越频率相差较大,因而,在汶川波激励下,桥梁结构地震响应较小;挡块-垫石的最大碰撞力基本上随着挡块-垫石间距的增大而呈减小趋势,但最大碰撞力不一定出现在挡块-垫石间距最小时,如连续梁中墩挡块-垫石间的碰撞响应;墩底最大剪力与最大碰撞力随挡块-垫石间距变化的规律基本相同。在3种地震波作用下,综合墩梁最大横向相对位移、挡块-垫石最大碰撞力和墩底最大剪力等响应结果,当挡块-垫石间距为2~3 cm时,横向地震响应峰值均较小,为较合理的连续梁桥挡块-垫石间距。
3.2 横向挡块-垫石间距的优化
为了与设计值保持统一,取连续梁桥挡块-垫石的合理间距为2 cm,但通过计算发现,连续梁中墩墩底剪力响应往往很大且比边墩的剪力响应大很多,约为边墩的剪力响应的4倍,轨道系统进一步放大了墩底剪力分配的不均匀性。由图5可知:当主梁为刚性梁时,在主梁挡块未接触到垫石前,支座作为传力装置,与桥墩组成串联系统;当墩梁横向相对位移大于挡块与垫石的间隙时,挡块和支座组成并联系统,而后与桥墩组成串联系统,令Keff为“挡块+支座+桥墩”的等效刚度,F为桥墩横桥向受力,y为“挡块+支座+桥墩”系统的横桥向位移,挡块、支座和桥墩的横桥向刚度分别设为Kd,Kz和K0,当挡块发挥限位作用变形为Δl时,

由以上关系可以得出

式(5)为关于挡块-垫石间距ΔG的递减函数。挡块垫石间距的参数优化研究就是通过改变挡块垫石间距来调整全桥横桥向的刚度分配,以达到合理分配横向地震力的目的。本文以减小连续梁中墩墩底剪力响应且对其他横向地震响应影响不大为目标,具体做法有2类:一类是减小简支梁桥墩和连续梁边墩上挡块-垫石间距,以增加对应桥墩的等效刚度,增加边跨桥墩的地震力分配;另一类是增加连续梁中墩上挡块-垫石间距,以减小对应桥墩的等效刚度,进而减小连续梁中墩的地震力分配。分别通过调整简支梁挡块-垫石间距为1 cm(工况1)和2 cm(工况2)、连续梁边墩挡块-垫石间距为1 cm(工况4)以及连续梁中墩挡块-垫石间距为3 cm(工况5)共4种挡块-垫石间距,并将连续梁边、中墩挡块-垫石间距均为2 cm定义为工况3,输入El-Centro波、Taft波和汶川波,研究调整挡块-垫石间距后高铁连续梁桥横向地震响应的优化效果。在3种地震波作用下,时程分析结果表明2类挡 块-垫石间隙优化方案基本可以达到减小连续梁中墩墩底剪力响应且对其他横向地震响应影响不大的预定目标。以El-Centro波为例,各工况结果如表3所示。从表3可见:各个优化方案效果有所差别,其中以调整连续梁中墩挡块-垫石间距为3 cm方案优化效果最佳(工况5)。3种地震波下其优化结果如图13所示(其中,一些地震波下的碰撞加响应缺失表示优化后未发生碰撞)。
由图13可知:该挡块-垫石间距优化方案可显著减小连续梁中墩墩底剪力,在2种地震波(El-Centro波和Taft波)下墩底剪力峰值减幅均达13%以上,优化效果明显(需要说明的是,在汶川波作用下,连续梁中墩横向固定支座一直未发生破坏,因而优化效果不明显,Taft波作用下使得原本不发生碰撞的简支梁部分发生了1次碰撞,碰撞力不大,为596 kN,且挡块仍在弹性范围内工作)。由此可见:高铁连续梁边墩挡块-垫石间距为2 cm,中墩挡块-垫石间距为3 cm,这种不等间距布置比连续梁边、中墩等间距布置更合理,可有效降低轨道系统对墩底剪力分配不均匀性的放大作用。

表3 El-Centro波下各工况间隙优化对横向碰撞效应的影响Table3 Effects of optimized gaps in different conditions on transverse pounding responses of El-Centro wave
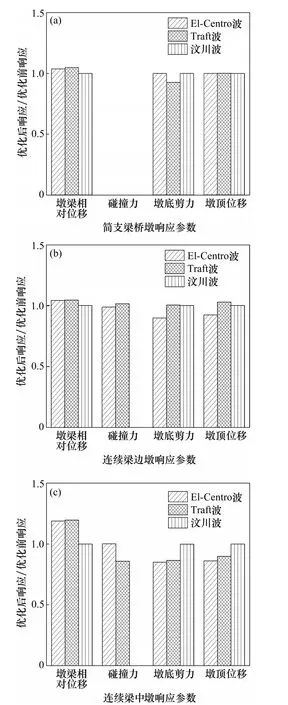
图13 间隙优化对横向碰撞效应的影响Fig.13 Effects of optimized gap on transverse pounding responses
3.3 橡胶缓冲挡块-垫石间距分析
工程上常在挡块垫石间加入橡胶垫层以减轻碰撞,其实质是对碰撞刚度和可变形范围的调整,进而也影响挡块垫石碰撞接触间隙。橡胶垫层特性采用combin40弹簧单元模拟,其刚度kp和阻尼cp可通过下式[20]计算:

式中:tp为橡胶垫层厚度;Ap为橡胶垫层的受压面积;Er为橡胶垫层的弹性模量,取为4.421 MPa;ξr为橡胶阻尼比,取为0.08。连续梁钢挡块加设橡胶垫片后的力学分析模型如图14所示。橡胶缓冲挡块间隙研究实质上就是对橡胶垫层厚度的调整,具体可以通过以下2个方案来进行:方案1,保持挡块-垫石间距2 cm不变,改变间距内的橡胶垫层厚度,具体取橡胶垫层厚度为0,1和2 cm;方案2,保持垫石碰撞接触间隙2 cm不变,改变橡胶垫层的厚度,具体取橡胶垫层厚度为0,1,2和3 cm。分别输入El-Centro波和Taft波,研究橡胶垫层厚度对高铁连续梁桥横向减碰效果(墩梁最大横向相对位移、挡块碰撞力和墩底剪力)的影响,结果如图15所示。
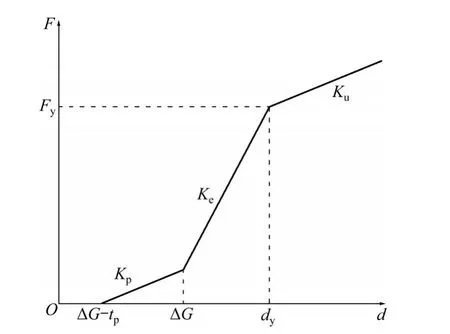
图14 挡块加设橡胶垫片的力-位移关系曲线Fig.14 Force-displacement curve of shear key combined with rubber bumper
由图15可知:方案1中在2 cm挡块垫石间距内改变了橡胶垫层厚度,随着橡胶厚度增加,连续梁墩梁最大横向相对位移基本呈减小趋势,挡块-垫石最大碰撞力随橡胶厚度的增加无明显变化规律。究其原因,一定厚度的橡胶一方面起到了缓冲作用,但同样也减小了碰撞发生的初始间隙,可能引起较大的碰撞力,因此,缓冲减轻碰撞作用实际上是这2个因素综合作用的结果。墩底最大剪力基本上呈减小趋势,当橡胶厚度为2 cm时,缓冲减震效果较好,但此时支座垫石对梁体的限制过强,影响梁体自由伸缩,即便在正常运营时,也可能会引发较多的碰撞,对橡胶耐久性也有一定影响。
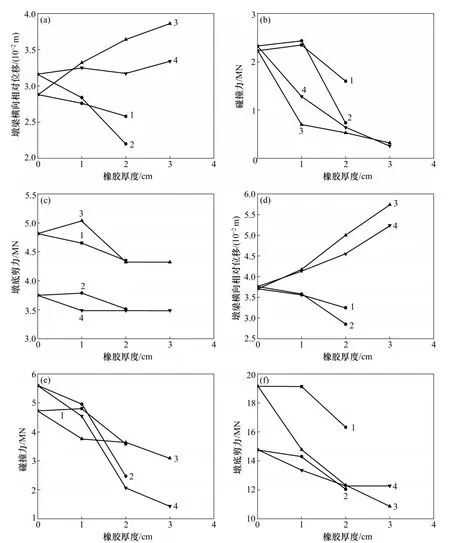
图15 橡胶厚度对横向减碰效果的影响Fig.15 Effects of rubber thickness on transverse pounding responses
方案2中保持2 cm厚垫石碰撞接触间隙不变,提高橡胶垫层的厚度有利于减小挡块碰撞力和桥墩地震响应,这是因为一定厚度的橡胶一方面起到了减小能耗的作用,另一方面也增加了挡块垫石间的接触间隙,因而缓冲减震效果明显,但同时也导致挡块限位效果下降,实际选用时应兼顾这2个方面的需求,选择合适的橡胶垫层厚度。经综合考虑,在2 cm厚垫石碰撞接触间隙外加入1 cm橡厚胶垫层缓冲效果较理想。
4 结论
1)轨道系统的约束作用会改变桥梁结构的横向动力特性与地震响应,增大桥梁横向刚度,放大墩底剪力横向分配的不均匀性。
2)限位挡块可有效降低墩梁横向相对位移,对横向限位防落梁起到重要作用,但挡块-垫石间的碰撞也增大了桥墩的地震响应。
3)针对本文工程算例,当连续梁桥墩挡块-垫石间距为2~3 cm时,横向地震响应峰值均较小;进一步提出了边墩、中墩挡块-垫石间距分别为2 cm和3 cm的优化方案,这种不等间距布置比连续梁边、中墩等间距布置更加合理,可有效降低轨道系统对墩底剪力分配不均匀性的放大作用。
4)在连续梁挡块间隙内加设橡胶缓冲装置会降低其墩梁横向相对位移、挡块碰撞力和桥墩地震响应,且防碰减震效果与橡胶厚度及布设方式有关。针对本文工程算例,经综合考虑,保持2 cm厚垫石碰撞接触间隙不变,在挡块上加设1 cm厚橡胶垫层缓冲效果较理想。

