自适应调整布谷鸟搜索算法研究
张毅 雷玉霞

摘 要:布谷鸟算法是基于启发式搜索的智能仿生算法。传统的布谷鸟算法收敛速度较慢,容易陷入局部最优解。针对该算法特点,对算法原理进行了分析,并就算法中步长和发现概率两个控制因素进行改进,使其根据迭代次数动态变化,提出了具有自适应调整特点的搜索算法,改变了步长和发现概率相应的更新方式,避免了传统布谷鸟算法容易陷入局部最优的缺陷,以增强算法搜索性能。实验对比表明,自适应调整的布谷鸟算法具有更好的寻优性能。
关键词:布谷鸟算法;自适应;搜索算法
DOI:10. 11907/rjdk. 182613 开放科学(资源服务)标识码(OSID):
中图分类号:TP312 文献标识码:A 文章编号:1672-7800(2019)008-0056-03
Research on Adaptive Adjustment of Cuckoo Search Algorithm
ZHANG Yi, LEI Yu-xia
(Department of Information Science & Engineering, Qufu Normal University, Rizhao 276800, China)
Abstract: The cuckoo algorithm is an intelligent bionic algorithm based on heuristic search. The traditional cuckoo algorithm has a slow convergence speed and is easy to fall into the local optimal solution. According to the characteristics of the algorithm, the algorithm principle is analyzed. The two control factors of the step size and discovery probability are improved, so that they change dynamically according to the number of iterations. A search algorithm with adaptive adjustment characteristics is proposed, which changes the step size and the update probability corresponding to the discovery probability, and make the traditional cuckoo algorithm avoid to fall into local optimum so as to enhance the search performance of the algorithm. After experimental comparison, the adaptively adjusted cuckoo algorithm has better performance.
Key Words: cuckoo algorithm; adaptive; search algorithm; algorithm optimization
作者简介:张毅(1992-),男,曲阜师范大学信息科学与工程学院硕士研究生,研究方向为智能信息处理;雷玉霞(1976-),男,博士,曲阜师范大学信息科学与工程学院副教授、硕士生导师,研究方向为智能信息处理、概念格。
0 引言
布谷鸟搜索算法(Cuckoo Search Algorithm,CS)是根据自然界中布谷鸟寻找合适的鳥窝产蛋繁殖的仿生算法,该算法参数较少,简单高效,容易实现,具有全局收敛性[1-3]。但是该算法容易陷入局部最优, 因此不少学者从基于步长和发现概率等方面提出改进方法。例如,Walton[4]对莱维飞行的随机步长进行了改进,Wang[5]提出用混沌序列作为步长改进,李荣雨等[6-7]提出对步长进行自适应改进,还有学者通过改变发现概率使其具有动态性来加快收敛速度[8-9]。固定的步长会使算法在求解过程中容易越过最优解,固定的发现概率会在搜索最优解过程中增加迭代成本,单独对步长或发现概率的控制有一定局限性。因此,Valian[10]提出动态调整发现概率和步长思路。受此启发,本文针对后期算法收敛速度慢、寻优精度低的问题,分析布谷鸟的搜索策略和特点,提出从步长和发现概率两个因素综合进行改进,随迭代次数的增加进行自适应参数调整,提高算法性能。经过标准函数和问题实例测试,将改进后算法与原算法进行比较研究。
1 布谷鸟搜索算法
布谷鸟繁殖后代方式是通过将鸟蛋产在其它鸟类的鸟巢中,由宿主孵化鸟蛋。有些情况下宿主会发现布谷鸟的鸟蛋,发现后将其抛弃,这样会使布谷鸟繁殖失败。
将自然界布谷鸟繁殖演变为算法后,约定如下3个假设规则[1]:
假设1:布谷鸟自由选择鸟巢产蛋,一个鸟巢只产一只蛋;
假设2:存在有最合适的布谷鸟蛋会传递保留到下一代;
假设3:鸟巢的数量固定,寄主发现鸟蛋的概率是[Pa],如果被寄主发现,鸟蛋将会被破坏,随之被放弃。
所以,布谷鸟鸟蛋所在的鸟巢就是一个解,寻优的过程就是不断用新解代替上一次的较差解,在算法中主要依靠随机游动和莱维飞行这两个环节产生新解搜索。
图1 莱维飞行轨迹
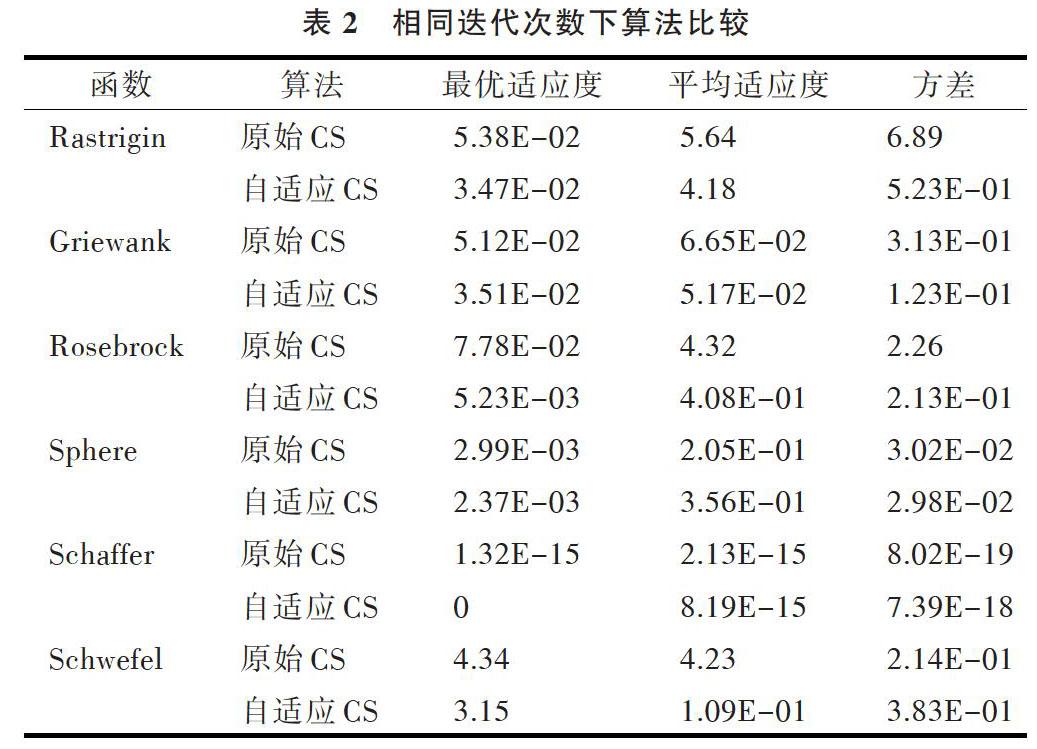
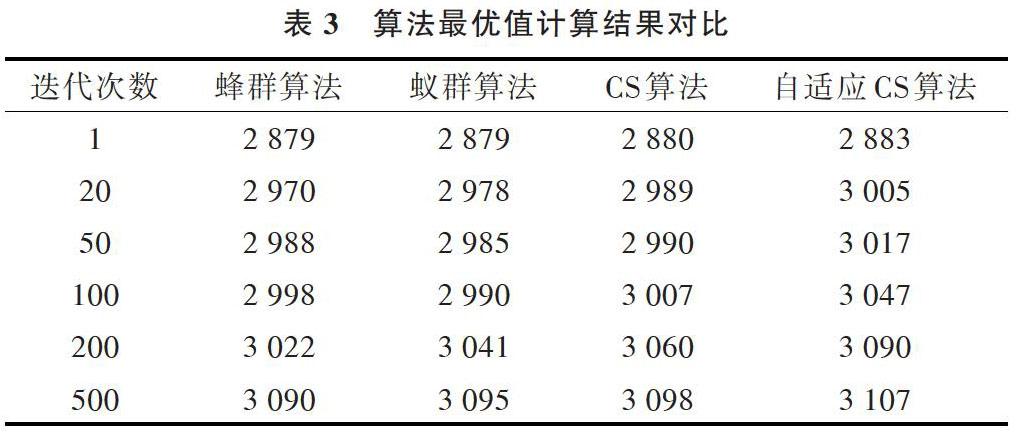
布谷鸟算法用随机游动产生新解:
[Xi+1=Xi+α⊕Levy(β)] (1)
其中:[i=1,2,3,?,n],[α]为步长控制量,[⊕]为点对点乘法,[Levy]为莱维飞行搜索,服从[Levy]分布式。
[L(s,λ)~s-λ,λ∈(1,3]] (2)
S属于莱维飞行的随机步长,通过莱维飞行进行位置更新后,随机产生0到1的数r,与鸟窝的发现概率[Pa]进行比较,如[r>Pa]则继续进行位置更新,[r 布谷鸟算法流程如下:①初始化设置相应参数,随机生成初始解并计算初始解的适应度;②通过莱维飞行产生新解;③计算新解的适应度;④通过发现概率[Pa]对解进行淘汰;⑤通过随机游动产生新解,替代被丢弃的解;⑥保留最好的解,回到第②步循环。 2 自适应调整布谷鸟搜索算法 在布谷鸟算法中,有4个参数控制算法,分别是鸟巢数量n、发现概率[Pa]、步长[α]、莱维飞行公式中的[λ]。通常情况下,[λ]=1.5,n=30(原标准CS算法设定[2]),这两个参数对算法的影响可以忽略不计。步长[α]和发现概率[Pa]影响算法的搜索性能,因此本文从这两个方面进行改进。 2.1 步长[α]的改进 在布谷鸟算法中步长[α]是固定的,在步长保持不变的情况下无法达到更加精确的搜索,只能增加迭代次数。本文将步长的改进与迭代次数相关,使步长伴随着迭代次数的增加逐渐呈动态指数递减变化,采用这种指数递减的动态步长可提高搜索精度,公式如下: [α(t)=α(t)?tmax?exp(-titmax)] (3) 其中,[ti]是当前迭代的次数,[tmax]是总迭代次数。 2.2 发现概率[Pa]的改进 布谷鸟算法中发现概率[Pa]决定是否保留当前解,它的取值会影响最优解搜索效果,若要把发现概率的取值调整为最佳就要使其动态变化。改进后的发现概率通过适应值可更好地区分解的优劣。方法是发现适应值更好的解的概率小于发现适应值差的解的概率,从而保留适应值更好的解,公式如下: [Pa,i=nPa(t)fij=1nfj] (4) 其中,[Pa,i]表示第i个鸟巢中蛋被发现的概率,n表示鸟巢的数目,[Pa(t)]表示当前的迭代次数下布谷鸟蛋的平均发现概率,[fi]表示当前第i代适应值,[fj]表示第j代适应值(最大迭代次数)。 3 实验与分析 算法测试环境为:Window 7,CPU为酷睿i5,内存8G,Matlab 7.0,测试函数包含:Rastrigin、Griewank、Rosebrock、Sphere、Schaffer、Schwefel。算法中鸟群规模参数n=30,发现概率[Pa=0.25],最大迭代次数[tmax=1 000],平均独立运行30次。 表1 标准测试函数 仿真图像横坐标为算法迭代次数,纵坐标为适应度,实验结果见图2-图7及表2所示。 图2 Rastrigin收敛曲线 图3 Griewank 收敛曲线 图4 Rosebrock收敛曲线 图5 Sphere收敛曲线 图6 Schaffer 收敛曲线 图7 Schwefel收敛曲线 表2 相同迭代次数下算法比较 函数测试显示,对于单峰Schaffer、Schwefel函数效果比较明显,凸显收敛优势。对于多峰Rastrigin、Griewank函数,搜索性能改進有限,但算法性能整体上有所提升。为进一步检验改进后算法的寻优性能和效率,采用经典的0-1背包问题作为应用测试实例:设物品个数N=50,背包容量C=1 000,重量W={80,82,85,70,72,70,66,50,55,25,50,55,40,48,50,32,22,60,30,32,40,38,35,32,25,28,30,22,50,30,45,30,60,50,20,65,20,25,30,10,20,25,15,10,10,10,4,4,2,1},价值V={220,208,198,192,180,180,165,162,160,158,155,130,125,122,120,118,115,110,105,101,100,100,98,96,95,90,88,82,80,77,75,73,72,70,69,66,65,63,60,58,56,50,30,20,15,10,8,5,3,1},见表3。 表3 算法最优值计算结果对比 图8 4种算法的收敛性对比 实验对比表明,自适应CS算法与解决0-1背包问题的经典智能蚁群算法、蜂群算法和原始CS算法相比,具有更好的收敛性能和搜索能力,见图8。 4 结语 布谷鸟算法与其它智能算法相比,具有通用性好、鲁棒性强的优点。针对其后期收敛速度慢、精度不高等不足,本文提出根据迭代次数调整的自适应布谷鸟算法,改写算法的步长和发现概率公式,提高算法搜索效率。采用测试函数和实际问题用例进行测试,实验表明该改进算法在收敛速度和寻优性能上均有提高。后续工作将进一步探讨更优的寻优策略应用于更多优化问题。 参考文献: [1] YANG X S, DEB S. Cuckoo search via levy flights[J]. Mathematics, 2010(1):210 - 214. [2] YANG X S, DEB S. Cuckoo search via lévy flights[C]. Nature & Biologically Inspired Computing, 2009. NaBIC 2009. World Congress on. IEEE, 2010:210-214. [3] 王凡,賀兴时,王燕,等. 基于CS算法的Markov模型及收敛性分析[J]. 计算机工程,2012, 38(11):180-182. [4] WALTON S,HASSAN O,MORGAN K,et al. Modified cuckoo search: a new gradient free optimisation algorithm[J]. Chaos Solitons & Fractals, 2011, 44(9):710-718. [5] WANG L,ZHONG Y. Cuckoosearch algorithm with chaotic maps[J].Mathematical Problems in Engi-neering,2015,9(4):623-635. [6] 李荣雨,戴睿闻. 自适应步长布谷鸟搜索算法[J]. 计算机科学, 2017,44(5):235-240. [7] 郑洪清,周永权. 一种自适应步长布谷鸟搜索算法[J]. 计算机工程与应用,2013, 49(10):68-71. [8] WANG L,YANG S,ZHAO W. Structural damage identification of bridge erecting machine based on improved cuckoo search algorithm[J]. Journal of Beijing Jiaotong University, 2013, 37(4):168-173. [9] 胡欣欣. 求解函数优化问题的改进布谷鸟搜索算法[J]. 计算机工程与设计,2013,34(10):3639-3642. [10] VALIAN E,MOHANNA S,TAVAKOLI S. Improved cuckoo search algorithm for global optimization[J]. Computers & Industrial Engineering, 2011(1):152-160. [11] 王李进,尹义龙,钟一文. 逐维改进的布谷鸟搜索算法[J]. 软件学报,2013,24(11):2687-2698. [12] PAVLYUKEVICH I. Levy flights, non-local search and simulated annealing[J]. Mathematics, 2007, 226(2):1830-1844. [13] 兰少峰,刘升. 布谷鸟搜索算法研究综述[J]. 计算机工程与设计,2015(4):1063-1067. [14] 秦岭,戴睿闻. 具有记忆性的自适应布谷鸟搜索算法[J].微电子学与计算机,2017,34(3):15-19,24 [15] 林要华,梁忠,胡华平. 贝塔分布的布谷鸟搜索算法[J]. 南京大学学报:自然科学版,2016, 52(4):638-646. [16] SHLESINGER M F. Mathematical physics:search research[J]. Nature,2006,443(7109):281-282. [17] 张晓凤,王秀英. 布谷鸟搜索算法综述[J]. 计算机工程与应用,2018,54(18):8-16. [18] 孙敏,房明磊,韦慧. 基于自适应步长的改进布谷鸟算法[J]. 赤峰学院学报:自然科学版,2018,34(7):45-49. [19] 林诗洁,董晨,陈明志,等. 新型群智能优化算法综述[J]. 计算机工程与应用,2018,54(12):1-9. [20] 钱伟懿,候慧超,姜守勇. 一种新的自适应布谷鸟搜索算法[J]. 计算机科学,2014,41(7):279-282. [21] 余建平,周新民,陈明. 群体智能典型算法研究综述[J]. 计算机工程与应用,2010,46(25):1-4,74. (责任编辑:杜能钢)

