基于Horseshoe+先验的惩罚置信区域变量选择方法

钱 彤,朱永忠

(河海大学 理学院，江苏 南京 211100)

0 引言

考虑高维稀疏线性回归问题:

y=Xβ+ε，

(1)

其中y表示响应变量，y∈Rn，X表示回归矩阵x∈Rn×p，β则表示估计的回归系数向量，β∈Rp，其中p为预测变量数，n为样本观测数.另外，ε=(ε1,…,εn)是误差项，假设εi～N(0,σ2).在此回归模型中，pn，且假设p个变量中只有少数变量是“相关变量”，即只有少数变量的回归系数远离零值.这里记 “相关变量”个数为pn，本文只考虑pn=o(n)的情况.近年来，大数据带来的此类高维稀疏模型的估计已然成为许多领域(基因学，计量经济学，临床医学等)的重要问题.在此类问题中，由于样本协方差XTX奇异，常见的频率论方法，诸如最小二乘估计(OLS)，Lasso，Adaptive Lasso算法等很难处理.有效的变量选择方法很有必要.

在贝叶斯框架下，常见的变量选择方法包括随机搜索变量选择(SSVC)[1]，贝叶斯正则化(包括贝叶斯Lasso[2]，贝叶斯Adaptive Lasso[3]等)，spike-and-slab先验变量选择[4]，以及全局-局部(global-local)收缩先验变量选择，例如Dirichlet-Laplace(DL)先验[5]，广义doubel-Pareto(GDP)先验[6]，Horseshoe先验[7]以及Horseshoe+先验[8]等.这些变量选择方法都是依赖计算出的后验包含概率(对于每个变量或每个模型)的阈值化，来选择最终纳入模型中的变量，从而得出最终稀疏模型.

Bondell(2012)[9]提出的贝叶斯惩罚后验置信区域变量选择法，将模型拟合与变量选择2个步骤分离，依赖于后验置信区域来寻找最稀疏模型.该方法只需要设置1个全模型的先验∏(β)，而避免了对模型空间设置先验.为了便于分析，该方法在模型拟合步骤使用了一个共轭正态先验：

β|σ2,τN～N(0,σ2/τN),

(2)

其中σ2是误差方差，τN是精确度参数，表示先验精度与误差精度的比率，控制收缩程度.通常给参数σ2一个逆Gamma超先验，给参数τN一个固定值或1个Gamma超先验.

传统的全局-局部(global-local)收缩先验类可以表示成正态先验的全局-局部尺度混合[10]：

(3)

其中τ是全局收缩参数，控制向量β的整体收缩.λj是局部收缩参数，控制βj的不同程度收缩.π(·)表示适当的先验分布.全局-局部先验类的密度函数在零点处的“峰值”与其“重尾”的特点，使得在处理稀疏问题时，往往能够“重”压缩小系数，“轻”压缩大系数.其中，Bhadra(2015)针对“超稀疏信号勘测”提出了Horseshoe+先验.该先验是著名的Horseshoe先验的拓展，并且在Horseshoe先验的理论优势基础上，具有更高的后验集中度，对小系数的压缩更 “重”，对大系数“轻”压缩甚至不压缩，使大系数估计的后验均方误差更小.因此在高度稀疏模型中的变量选择效果更好.

为此，本文改进贝叶斯惩罚置信区域法，基于正态先验在稀疏问题中的表现不佳，将原方法中的正态先验替换成Horseshoe+先验，这样做的优势在于：一是Horseshoe+先验的贝叶斯分层模型能够进行块更新，从而可以应用Gibbs抽样;二是提高模型拟合产生的后验集中度，从而提高该方法的变量选择效果.

1 模型及方法

1.1 惩罚置信区域法

Bondell等于2012年给出了惩罚置信区域法的详细介绍.

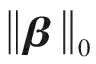
(4)

(5)

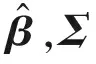
(6)

其中cα是与α有关的值.对τ设置一个先验就不能产生“椭圆型”后验分布了.但是，我们仍然可以使用“椭圆型”轮廓来产生置信区域，尽管对应的后验置信区域不再是最高后验密度区域，但是依然是合理的.因为“椭圆型轮廓”也是最高后验密度区域的一个合理的近似.

使用一个L0与L1之间的光滑同伦[11]以及局部线性近似[12]来解决上述目标函数求解时间复杂度高以及可能存在不唯一解的问题，得出最终的最优化问题：

(7)

其中λα是与α,cα一一对应的值.随着置信水平α的变化，将会产生一个预测变量的有序集，其中，越“重要”的变量越排在集合的前面.

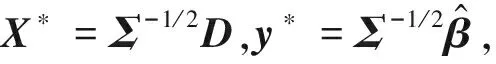
1.2 Horseshoe+分层模型

将Bhadra(2015)提出的Horseshoe+先验应用到线性回归模型中，为了使估计过程更加稳健，考虑响应变量y=(y1,y2,…,yn)与回归系数β=(β1,β2,…βp)的抽样分布模型如下：

(8)

其中π(σ2)表示对误差方差构造的先验，C+(0,κ)是一个标准半柯西分布，概率密度函数为：

(9)

由于半柯西先验的后验分布本身缺乏标准的形式，Enes(2015)针对Horseshoe先验提出了一种直观的抽样方法，通过添加一个辅助变量φj，半柯西分布可表示成逆Gamma分布的尺度混合[14]：

(10)

利用逆Gamma分布的共轭性，可以直接通过Gibbs抽样计算后验分布，大大减少了计算复杂度.为了给每一个参数构建一个具有封闭形式的条件后验分布，沿用上述方法，进一步添加2个潜在变量γ,ωj，可对参数λj,τ采用如下的全条件分层结构：

(11)

1.3 Gibbs抽样

考虑到在所有参数的先验分布已知的情况下，各参数的全条件分布容易抽样，于是可通过Gibbs抽样来推导出各参数的全条件后验分布：

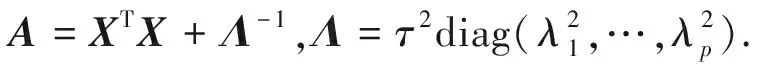
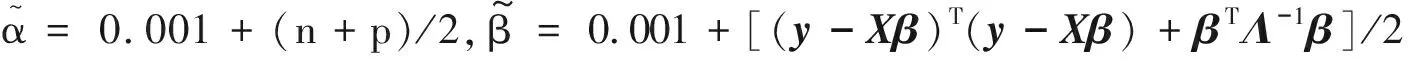
全局收缩参数τ与局部收缩参数λj以及四个潜在变量ηj,φj,γ,ωj的全条件后验分布根据共轭性服从逆Gamma函数：

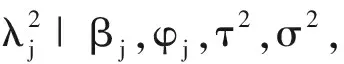
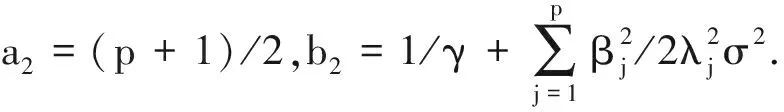
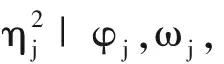
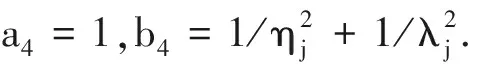
5)抽样γ|τ2，其全条件后验分布为逆Gamma分布IG(a5,b5)，其中a5=1,b5=1+1/τ2.

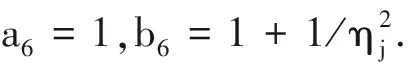
2 数据仿真

Bondell(2012)已经证明了基于正态先验的惩罚置信区域方法在变量选择效果上优于SSVS，Lasso，adaptive Lasso，Dantzig Selector以及SCAD等方法.在此基础上，本文主要比较基于不同先验的惩罚置信区域法的变量选择效果以及预测精度.通过在不同稀疏程度的高维线性回归的情况下比较基于Horseshoe+先验，Normal先验的惩罚置信区域方法的变量选择效果和预测精度，为增加对比，我们同时还考虑了Bayesian Lasso与Lasso的情况.其中Bayesian Lasso相当于给系数β一个Laplace先验：β|σ,τL～DE(σ/τL)，式中DE(a)表示一个均值为0的Laplace分布.为便于分析，以上所有先验中的误差方差σ2统一分配一个逆Gamma先验IG(0.001,0.001).与Bondell(2012)实验相同，给Normal先验中的超参数τN分配一个Gamma先验Gamma(0.01,0.01)，且Bondell(2012)通过实验模拟证明超先验Gamma(a,a)中的参数a对实验结果不敏感.同理，Laplace先验给超参数τL一个”无”信息先验Gamma先验Ga(1,1).另外，Lasso算法选用Efron提出的5折交叉检验的LARS算法.利用R软件来实现后验计算中的Gibbs抽样.

针对(1)式线性模型，

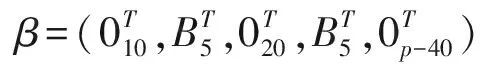
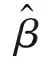
2.1 变量选择效果

为了衡量上述方法得出的变量排序的准确性，考虑变量排序每一步的模型准确度.对排序的每一步，引入指标TP(True Positive)、FP(False Positive)，TN(True Negative)，FN(False Negative)分别表示正确选择进模型的真相关变量、错误选择进模型的假相关变量、正确排除在模型外的真不相关变量、错误排除在模型外的假不相关变量.进而引入指标TPR(True Positive Rate)或称specificity，FPR(False Positive Rate)或称1-specificity，其中TPR等于TP占真实相关变量的比例，FPR等于FP占真实不相关变量的比例.以FPR为x轴，TPR为y轴，绘制ROC(Receiver Operating Characteristic)曲线.根据ROC曲线下的平均AUC(Area Under ROC Curve)面积值进行比较.通常，AUC的值介于0.5与1之间，较大的AUC值表示变量选择效果更好.对于仿真一和仿真二的AUC值见表1～表5.

表1 p=50对应的2个仿真实验中的AUC值

表2 p=200对应的2个仿真实验中的AUC值

表3 p=500对应的2个仿真实验中的AUC值

表4 p=1000对应的2个仿真实验中的AUC值

表5 p=2000对应的2个仿真实验中的AUC值

根据表格中的数据，可以得出结论：当真实线性回归模型中的相关变量回归系数产生自均匀分布U(0,1)，即大多接近0时，随着维度的增加，Horseshoe+先验的AUC值与Normal先验的以及Laplace的AUC值相差不大.且在相关系数较高的情况下Horseshoe+先验表现出略微的劣势.当然，Lasso算法仍然存在处理相关性高的数据时效果差的弊端；当真实回归模型中的重要回归系数产生自均匀分布U(0,5)，即包含接近0的系数以及远离0的系数，这种情况也更接近于现实数据.在这种情况下，Horseshoe+先验的优势更加突出，即使在相关系数高的情况下，依然表现出绝对的优势.这一结论是符合预期的，因为在理论上，Horseshoe+先验面对高维稀疏回归问题，对大系数“轻”压缩，对小系数“重”压缩的特点，使得在该类问题中产生更加集中的后验分布，对大系数估计的后验均方误差更小.尤其是在仿真二实验中，存在较大的回归系数的情况下，该优势更加突出.从而在惩罚置信区域的方法中更易找出准确的最稀疏解，变量选择效果更好.总的来说，基于Horseshoe+先验的惩罚置信区域法在高维稀疏回归问题中的变量选择效果，尤其是在真实回归系数同时包含小系数与大系数的回归问题中，优于Normal先验与Laplace先验.

2.2 预测精度

为了验证该变量选择方法产生的相关变量排序应用到预测中的效果，以及变量排序每一步的准确性，我们考虑仿真一以及仿真二实验中，p={50,500,200 0}，ρ={0.5,0.9}的情况，独立产生满足仿真条件的20个测试集，根据50个训练集产生的相关变量排序，依次选取不同数量的预测变量纳入预测模型内，计算出20个测试集的平均预测均方根误差RMSEP，并绘制出以上模拟实验中20个测试集的平均预测均方根误差.见图1～图12.

(12)

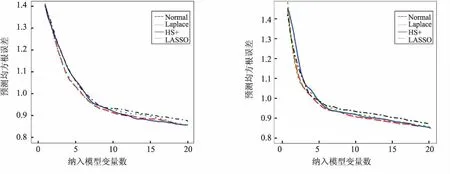
图1 仿真一p=50,ρ=0.5平均预测均方根误差 图2 仿真一p=50,ρ=0.9平均预测均方根误差

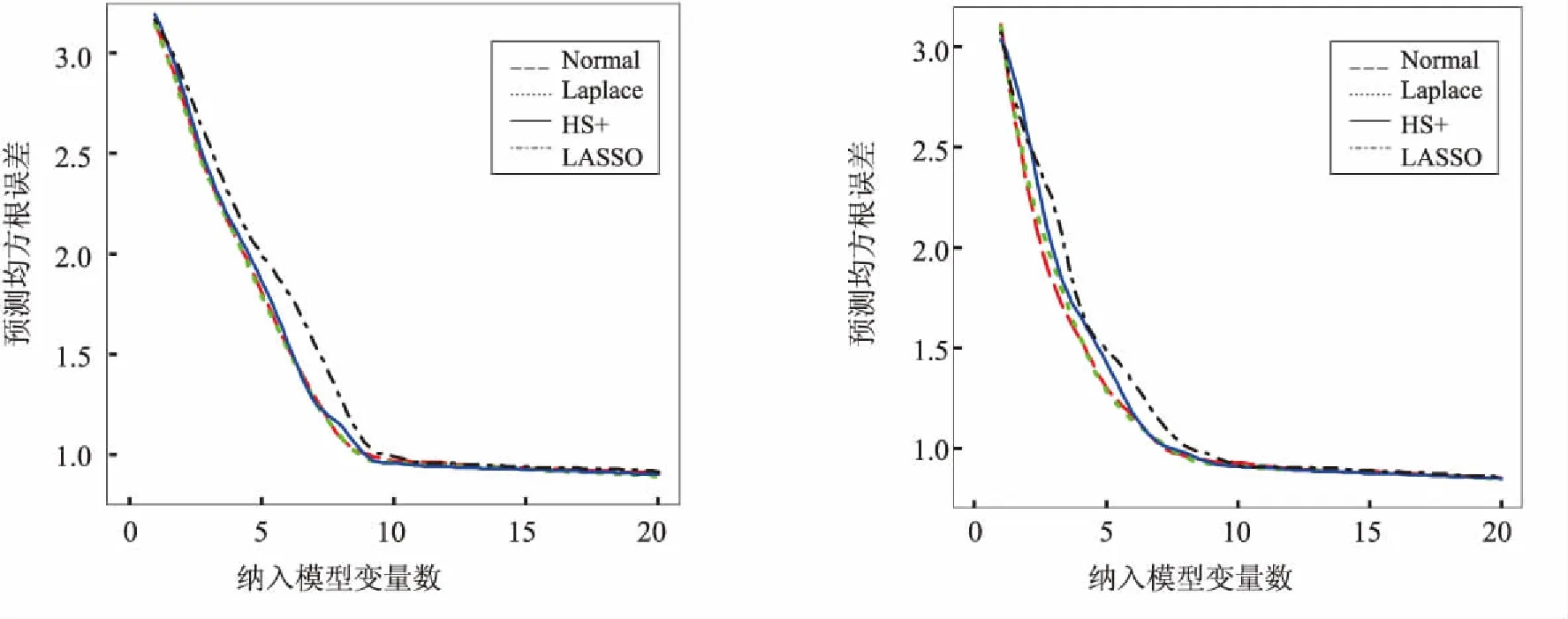
图3 仿真二p=50,ρ=0.5平均预测均方根误差 图4 仿真二p=50,ρ=0.9平均预测均方根误差

图5 仿真一p=500,ρ=0.5平均预测均方根误差 图6 仿真一p=500,ρ=0.9平均预测均方根误差

3种先验对应的曲线都呈现出一个递减趋势，且在区间(5,10)间递减速率开始下降，在区间(10,20)之间递减速率继续下降，趋于平稳.这是符合预期的，因为相关变量只有10个，因此将10个变量纳入最终模型时，大约已包含了所有相关变量，且在纳入大于10个变量时，预测均方根误差基本没有太大变化.递减速率逐渐下降说明产生的相关变量排序是按照重要性的大小，越重要的变量排在越前面.

当p=50时，Horseshoe+先验对应的预测均方根误差曲线与Normal先验与Laplace先验差异不大.随着p逐渐增大，即稀疏度越来越高，Horseshoe+先验对应的预测均方根误差曲线逐渐低于其他两个先验的误差曲线，预测效果更好.当然，在仿真一实验中，当相关系数ρ=0.9时，Horseshoe+先验的预测误差曲线只在前半部分低于其他两个先验的误差曲线，说明基于Horseshoe+先验的惩罚置信区域法在处理相关系数高的数据时，选择出全部相关变量的效果不够好,但在前半部分选择出较重要变量的能力更好.一个合理的解释正如Juho(2016)指出[15]，当样本数据之间存在强相关性时，Horseshoe+先验中的全局参数τ通过样本数据被强识别的能力较弱.但是，在仿真二实验中，基于Horseshoe+先验的预测误差总是低于其他2个先验的误差，且当选择纳入模型的变量数接近10时，预测误差达到最低，之后趋于平稳，说明几乎准确选择出所有相关变量.总的来说，基于Horseshoe+先验的惩罚置信区域法的预测效果优于Normal先验与Laplace先验.

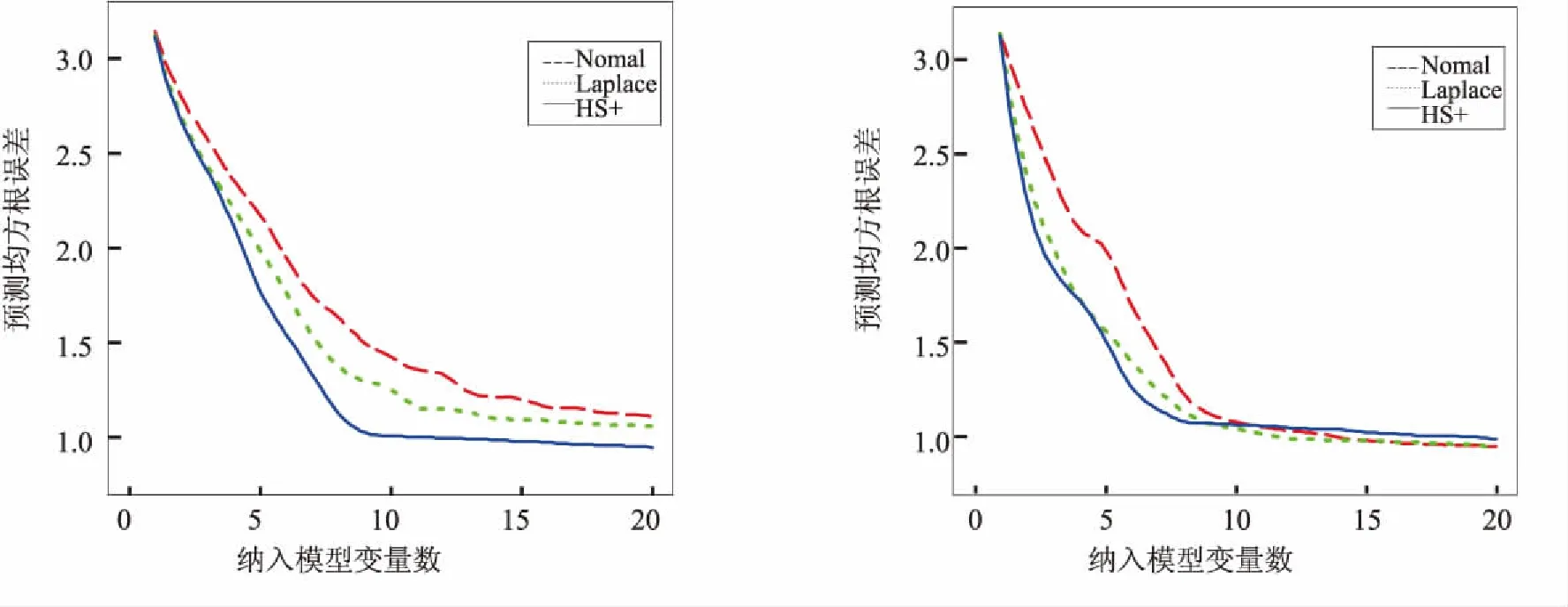
图7 仿真二p=500,ρ=0.5平均预测均方根误差 图8 仿真二p=500,ρ=0.9平均预测均方根误差

图9 仿真一p=2000,ρ=0.5平均预测均方根误差 图10 仿真一p=2000,ρ=0.9平均预测均方根误差

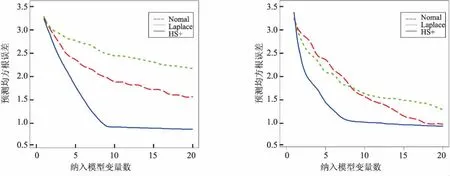
图11 仿真二p=2000,ρ=0.5平均预测均方根误差 图12 仿真二p=2000,ρ=0.9平均预测均方根误差

3 结语

在高维稀疏线线性回归问题中，变量选择这一步骤很重要.本文针对这一问题，在惩罚置信区域变量选择方法的基础上，利用该方法在高维线性回归问题中的优异表现，以及Horseshoe+先验在高维稀疏变量选择问题中的应用，将两者有效结合.将Horseshoe+先验应用到该方法中，取代原方法使用的共轭正态先验.利用Horseshoe+先验在高维稀疏问题中对大系数“轻”压缩，对小系数“重”压缩的特点，产生更好的后验集中度与后验估计，从而提高变量选择准确性.通过数据模拟实验结果可以得出结论，在高维稀疏回归问题中，基于Horseshoe+先验的惩罚置信区域法相比于正态先验与Laplace先验，变量选择效果与预测效果总体上更好.

当然也存在一些不足，本文只将基于Horseshoe+先验的惩罚置信区域变量选择方法与原始方法中的正态先验以及Laplace先验进行了对比，实际上，惩罚置信区域方法可以与多种先验结合，为此，可进一步研究基于不同先验的惩罚置信区域方法，从而提高原方法的变量选择效果及预测效果.