时变波动率下ARIMA族触发式理财产品定价

邱明雪,孙玉东

(1.贵州民族大学 数据科学与信息工程学院,贵州 贵阳 550025;2.贵州民族大学 商学院,贵州 贵阳 550025)

金融理财产品是商业银行在对潜在目标客户群分析研究的基础上,针对特定目标客户群开发设计并销售的资金投资和管理计划,是期权的延伸,其定价也是金融数学的重要研究内容.

目前已有许多关于金融理财产品定价研究的文献.文献[1]以区间型股票挂钩类结构性产品为研究对象,结合股票波动率和多资产相关性的动态特征,运用蒙特卡罗模拟方法,提出区间型金融理财产品的定价方法,同时进行了偏差性检验.杨招军等[2]考虑到市场非完备和投资者风险厌恶的实际情形,基于效用无差别定价原理,利用随机控制方法得到金融理财产品价格的偏微分方程,并用有限差分法进行数值分析.陈金龙等[3]应用Cholesky分解方法,解决了资产间的相关性问题,然后针对多资产保本型股票挂钩结构性产品收益函数特点,利用蒙特卡罗方法对金融理财产品进行相应的定价.文献[4]研究了金融理财产品定价的效率问题,使用数据包络分析方法(DEA)对我国商业银行理财市场的定价效率进行了实证分析.

近年来,随着我国金融市场的发展,各商业银行涌现出了一些新的理财产品,触发式理财产品就是其中的一种,其基本内容可概括为表1.触发式理财产品的收益可以分为三部分内容.

1)在存续期[0,T]内,若理财产品挂钩的风险资产触及过行权价格P1和P2,则理财产品的收益率为r1,此时单位本金的收益为1+r1T;

2)在存续期[0,T]内,若理财产品挂钩的风险资产触及过行权价格P1但未触及过行权价格P2,则理财产品的收益率为r2,此时单位本金的收益为1+r2T;

3)在存续期[0,T]内,若理财产品挂钩的风险资产未触及过行权价格P1和P2,则理财产品的收益率为r3,此时单位本金的收益为1+r3T.

表1 挂钩于欧元兑美元汇率的触发式理财产品(起购金额:50 000元)

经归纳总结,其到期日的收益可以归结为如下公式:

(1)

其中随机过程{S(t),t≥0}表示欧元兑美元的汇率,其随机结构稍后给出.

令人遗憾的是,有关触发式理财产品定价的文章还不多见,主要是因为触发式理财产品收益结构复杂,难以定价.文献[5-6]假定波动率和期望收益率为常数,研究了此类理财产品的定价问题.

当波动率和期望收益率不为常数时,触发式理财产品的解析定价是困难的,从而这里研究了触发式理财产品定价的Monte-Carlo方法.以欧元兑美元的汇率数据为基础进行统计分析,以便确定理财产品挂钩的风险资产价格模型,进而采用鞅方法和Monte-Carlo技术,确定触发式理财产品在到期日的收益.

1 欧元兑美元汇率数学模型

本节在时间区间2017年11月30日至2018年01月20日上收集了12组欧元兑美元汇率数据.每组汇率数据内部均采用6 h为时间间隔,受开盘制度的影响(周末不开盘),每周按照时间顺序连续采集20个数据.

汇率数据用于分析和推断触发式理财产品挂钩的随机模型,并依据此模型研究触发式理财产品定价问题.对每组数据取对数并差分,将处理之后的数据逐次串接,这里称之为混合数据.本文将借助这些混合数据判断欧元兑美元汇率遵循的随机模型.

先对混合数据进行单位根检验,检验结果见表2,其中ADF检验和PP检验的P值小于0.05,KPSS检验的P值大于0.05,说明混合数据组成的序列是平稳的.

表2 混合数据的单位根检验

表3为Box白噪声检验结果,可以看出各组数据的P值均大于0.05,意味着这16阶混合数据不存在相关性.进一步做自相关系数图确认结果(见图1),可以看出100阶以内的自相关系数均在虚线以内,这说明混合数据不存在任何阶数的相关性.

表3 混合数据的Box检验

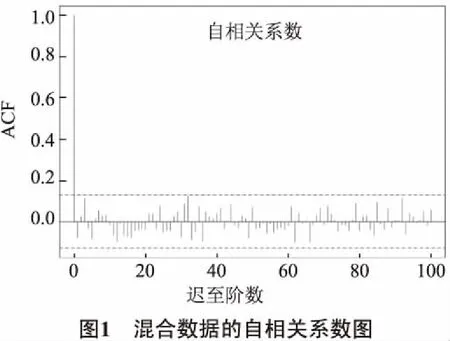
最后对混合数据进行KS正态性检验,P值为0.213 9,大于0.05,意味着其遵循正态分布.再进行t检验,P值为0.439 9,说明混合数据遵循0均值的正态分布.

综上所述,可以认定欧元兑美元的汇率数据取对数并差分之后是独立同分布的0均值正态序列,从而欧元兑美元的汇率应当遵循如下随机模型

dS(t)=σ(t)S(t)dB(t),

(2)

其中σ(t)表示波动率,它是时间的函数,{B(t),t≥0}为标准Brown运动.

2 触发式理财产品定价

假定当前时刻是t时刻,理财产品在0时刻购买,T时刻到期.由于欧元兑美元汇率在t时刻和t时刻之前的轨迹是已知的,从而触发式理财产品在t时刻的风险中性价格v为

v=exp{-r(T-t)}E[f(T)|Ft].

(3)

Monte-Carlo模拟的基本思想是:在风险中性测度下,先模拟多条欧元兑美元汇率的轨迹,利用每条轨迹模拟触发式理财产品在到期日的收益,再用这些收益的均值去替代公式(3)中的数学期望,进而得到触发式理财产品的价值.Monte-Carlo模拟方法的步骤大致分为以下几个方面.

2.1 日内波动率的预测

欧元兑美元汇率的历史数据是已知的,对不同日期汇率数据的对数差分进行Wilcoxon检验,结果见表4,可以发现有些P值大于0.05,有些P值小于0.05,说明不同日期汇率的对数差分数据之间并不满足独立同分布条件,而在上节已经验证它们的混合(混合数据)通过了Box检验,说明数据之间具备独立性,利用排除法可以认定不同日期汇率的对数差分数据不满足同分布条件.

表4 混合数据的Box检验

同时t检验的P值为0.439 9,说明不同日期的对数差分数据的均值和0无显著差异.而正态分布完全由均值和方差确定,再利用排除法可以认定不同日期的对数差分数据的方差不尽相同,说明对数差分数据的方差不满足一致性条件.最后通过Bartlett方差齐性检验得到P值为0.002 201,小于0.05,再次确认了不同日期的汇率对数差分数据确实不满足方差一致性条件.

综上所述,对汇率的对数差分数据的分析表明不同时期的金融市场具有不同的波动率.因此在进行触发式理财产品定价时,应该采用不同波动率的随机模型来建模.在经过检验之后,这里采用ARIMA模型进行建模.

依据固定时间间隔Δt获取的历史数据,提取日内波动率

σ(t-m),…,σ(t-2),σ(t-1),σ(t0),

其中m为采集数据的天数.针对此波动率序列,采用时间序列方法预测未来时刻的日内波动率

σ(t1),σ(t2),σ(t3),….

并假定对未来时刻波动率第j次预测为

σj(t1),σj(t2),σj(t3),….

2.2 欧元兑美元汇率轨迹的模拟

理论上欧元兑美元的汇率是连续的,但是在实际操作中获取的数据是离散的,获取数据的时间间隔最小也只能做到1 min(每隔1 min采集一个汇率数据),而且受计算机编程的限制,所分析的数据也必须是离散的.其中欧元兑美元的历史数据是已知的,并且已经检验汇率数据遵循随机模型(2),从而设定时间间隔

由公式(2)的Ito公式

(4)

公式(4)等号两侧对时间区间[ti-1,ti]进行积分,可以得到

(5)

由于B(ti)-B(ti-1)～N(0,Δt),i=0,1,…,n-1,并且当i≠j时,B(ti)-B(ti-1)和B(tj)-B(tj-1)相互独立,从而可以独立地生成一系列N(0,Δt)正态随机数ε1,ε2,…,εn,并逐次代入下面的公式

Sj(t0)=Sj(t),

(6)

(7)

(8)

(9)

由此得到欧元兑美元汇率的第j条轨迹,然后再模拟一次随机数ε1,ε2,…,εn,得到汇率的第j+1条轨迹,j=1,2,…,N-1.依次类推公式(6)-(9)的模拟过程,获取欧元兑美元汇率的多条轨迹

Sj(t0),Sj(t1),…,Sj(tn),j=1,2,…,N,

其中j表示对汇率的第j次模拟.

摘 要：在如今的教学中，翻转课堂应用越来越广泛，对改善课堂教学质量发挥出了巨大的作用。结合小学英语课堂教学的实际情况，对翻转课堂在小学英语教学中的应用以及效果进行了介绍，以期为相关人员提供借鉴。

2.3 触发式理财产品价格的Monte-Carlo模拟

考察汇率的第j条路径Sj(t0),Sj(t1),…,Sj(tn),触发式理财产品在到期日的收益为

Fpay-off(j)=f(T,Sj(ti),i=1,2,…,n),

(10)

其中j=1,2,…,N,依据公式(1)

重复公式(10)的产生过程,获取N个触发式理财产品的收益样本

Fpay-off(1),Fpay-off(2),…,Fpay-off(N).

(11)

由矩估计方法,用样本Fpay-off的均值代替公式(3)中的数学期望,于是触发式理财产品在t时刻收益的估计为

(12)

2.4 模拟精度和有效模拟次数

为了简便起见,令μ和σ2分别表示总体Fpay-off的均值和方差,即

μ=E[Fpay-off],σ2=Var[Fpay-off].

容易知道

(13)

(14)

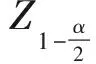
(15)

(16)

Step 1 选择合适的精度d作为估计量的标准误差(例如d=1,d=0.1,d=0.01);

Step 2 再选择合适的显著水平α,并产生大于100个汇率轨迹;

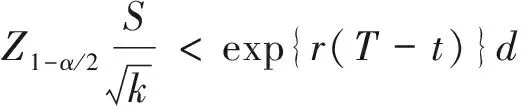
3 触发式理财产品定价

3.1 日内波动率的提取

采用1节中欧元兑美元汇率的对数差分数据,进行日内波动率的提取.假设第i天的对数差分数据为

xi,1,xi,2,…,xi,n.

根据公式(5)或者文献[7],日内波动率的估计为

(17)

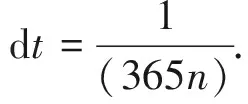
3.2 ARIMA模型的选取和定阶

对日内波动率序列进行单位根检验(见表5),可以看出ADF检验的P值小于0.01,PP检验的P值小于0.05,KPSS检验的P值大于0.1,说明日内波动率序列是平稳的,同时这也意味着可以采用ARIMA模型进行未来时刻日内波动率的预测.

表5 单位根检验的P值

图3为日内波动率序列的自相关系数图和偏自相关系数图,可以看出各阶自相关系数和偏自相关系数均在虚线以内,这也意味着未来时刻的日内波动率可以采用白噪声序列来预测.再进行KS正态性检验,可以得到P值为0.357 5,大于0.05,说明日内波动率数据可以用正态分布刻画.

容易计算日内波动率序列的均值为0.067 025 04,标准差为0.036 726 33,从而未来时刻的日内波动率可以采用下面的公式预测

σ(j)=0.067 025 04+0.036 726 33·ε(j),j=1,2,…,

其中j表示天数,σ(j)为第j天日内波动率的预测结果.

3.3 数值模拟

本节仍选取表1罗列的几款触发式理财产品.根据2018年2月18日的银行利率信息,选取无风险利率r=0.043 5,同时选取显著水平α=0.05,模拟精度设置为0.01,3款来自农业银行的触发式理财产品的模拟价格情况见表6,结果表明如果模拟次数不少于2 163 677次,则50 000本金的理财产品ADRY170209A,其自身价值为38.392 6,并且该结果以95%的概率精确到小数点后两位,其它2款理财产品依次类推.

继续分析Monte-Carlo模拟的精度问题,做触发式理财产品ADRY170174A价值与路径条数N的关系,如图4所示.可以看出,由Monte-Carlo方法计算出的触发式理财产品价格的收敛速度和N关系明显,并且图4中所示路径条数N最大为4 000条,在接近4 000条时,期权价格仍然在41与43之间震荡,收敛效果并不明显.由于收敛速度为O(N-0.5),要想达到一定的模拟精度,则路径条数N必须高于4 000万条,这也与有效模拟次数对应的结果相符.

表6 3款触发式理财产品的Monte-Carlo结果

4 结语

本文主要通过分析欧元兑美元的汇率数据,推断出汇率遵循的随机模型,并经过一系列的检验分析得出该模型波动率具有时变特性,由此建立了波动率的预测模型,随后利用Monte-Carlo方法对触发式理财产品的价值进行数值模拟,结果表明,若想达到一定的模拟精度,有效模拟次数需尽可能大,而对触发式理财产品ADRY170174A则要求其路径条数应高于4 000万条.