动态加权与区间二元语义结合的FMEA方法

刘龙，李斌

1.上海交通大学 生物医学工程学院，上海 200030；2.上海交通大学附属第六人民医院 医院管理研究中心，上海 200233

引言

故障模式与影响分析（Failure Mode and Effects Analysis，FMEA）作为一种评估和降低风险的方法，已被许多行业使用多年，如航空航天、汽车、电子和医疗行业[1-2]。与其他风险评估工具不同，FMEA的主要关注点是强调主动预防、处理与系统相关的问题，而不是在故障发生后被动地寻找解决方案。这可以帮助管理者调整现有的计划，采用建议的措施来降低故障发生的可能性，尽量避免危险事故。传统的FMEA使用风险优先数（Risk Priority Number，RPN）来评估故障模式的风险级别。RPN由故障模式的发生度（Occurrence，O)、严重度（Severity，S）、检测难度（Detectability，D）三个风险因子的乘积获得，即通常O、S、D的取值为1～10的等级。对所有故障模式依据RPN数值由大到小排序，数值越大说明风险越高，急需采取风险预防措施进行改善，使其RPN值降低到可接受水平。虽然传统FMEA是一种很有吸引力的风险分析工具，但许多文献认为其存在一些缺陷[3-6]，主要有：①D值通常难以精确估计，通常所获得信息是不确定或模糊的，且容易受到FMEA团队成员的主观因素影响；②为考虑O、S、D因素之间的相对重要性，对于特定的FMEA应用中，这三个因素往往具有不同的重要性；③不同的O、S、D值可以获得相同的RPN值，但其隐含的危险性可能完全不同；④RPN的计算公式值得商榷，其代表的数学含义受到质疑。

针对FMEA存在的上述缺陷，很多改进的FMEA被提出，使得FMEA成为更加灵活的系统风险评估管理工具。由于FMEA的评估过程可认为是多准则群策问题，而人对信息不完全的事物进行精确评估是比较困难的，区间的评估则会显得更容易得多，因此基于模糊理论的FMEA方法得到广泛应用。杨舟等[7]将O、S、D值的评估采用语义术语表示，通过模糊数学理论使得评估中模糊的、定量的或定性信息可以统一处理得到去模糊实数，使得评估过程更加灵活，贴近人的思维方式，但隶属度函数的确定缺乏一定的依据且存在主观问题。Chang等[8]通过灰色关联分析（Gray Relational Analysis，GRA）理论进行FMEA分析，以非常直接和简单的方式获得风险优先级，而不需要任何形式的实用函数。Braglia等[9]提出基于模糊TOPSIS的FEMA方法，实现了对失效模式的快速高校排序，并对敏感性进行了分析，验证了该方法对不同失效原因给出了合理、鲁棒的最终优先级排序。Liu等[10]提出一种基于模糊集理论和VIKOR方法的模糊FMEA方法来处理FMEA中的风险评估问题。Hu等[11]采用模糊层次分析法确定风险因素的相对权重。基于模糊理论的FMEA方法大多关注的是使用模糊逻辑处理实际情况中的不确定性，并将语言变量应用于FMEA方法[12]。然而，FMEA是一种群体决策过程，通常由多学科、跨职能团队执行，专家由于各自的专业知识和背景不同，常常使用不同的语言术语集来表达自己的评估意见[13]，针对特定的风险因素、失效模式产生不同类型的评估信息，其中一些可能是精确的或不精确的，确定的或不确定的，完整的或不完整的。传统的RPN方法和基于模糊逻辑的方法很难将这些不同类型的信息融合到FMEA中，并且，模糊语言在信息融合过程中由于初始表达域的离散不连续，容易导致信息丢失，使得运算后的结果难以精确对应到初始的术语集。因而Liu等[12]提出一种基于区间二元组语义模型的方法，在解决FMEA风险评估问题时，对自然语言的处理更加灵活和精确。该方法的优点是，FMEA团队成员可以使用不同粒度的语言术语集来表达他们的评估信息，语言信息域的连续性保证了信息融合过程中不会造成信息丢失。

通常FMEA的改进都涉及了风险因素的权重设定，并对FMEA成员之间赋予了不同权值，成员之间的权值往往是确定的实数，但这种做法默认为每个成员对不同风险因素评估结果的权威性或可信度是一致的，而实际应用中往往不符合。FMEA成员往往是跨职能、跨学科的，在对某个系统、部件或流程的故障的发生频率、影响程度或检测难度的把握上，理论上是存在偏差的。一些成员对某个故障模式的发生频率把握更加精确，但其对该模式检测难度可能把握薄弱些。一种改进的方法是给每个FMEA成员针对O、S、D三个因素分别确定一个权值使得决策过程更符合实际。基于此，本文提出动态加权与区间二元语义结合的FMEA方法，提出一种可行的方法确定FMEA成员在不同故障模式下对于不同风险因素的动态权值，并结合区间二元语义方法的灵活性，使FMEA成员可以使用不同粒度的语言术语集来表达各自的判断，有效捕获FMEA团队成员意见的多样性，并通过一个示例进行了本文方法的演示。

1 区间二元语义

二元语义模型首先由Herrera等[14]提出，能直接、全面地表达模糊环境下的语言型决策信息,避免信息转换过程中的信息丢失。决策者之间允许采用不同粒度的评估术语集。决策者的语言评估信息由二元语义组形式表示，Si为预设的离散有序语言评估术语集S的元素，ai为符号转换值，代表语义符号平移量，即语言评估信息相对于Si的偏差。

1.1 定义1

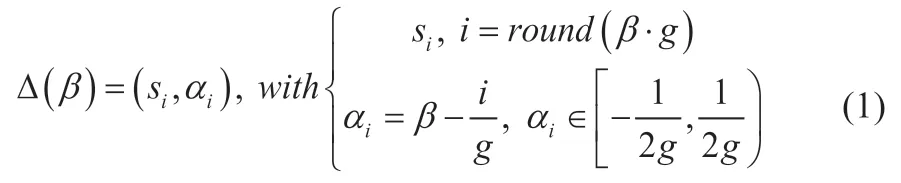
1.2 定义2

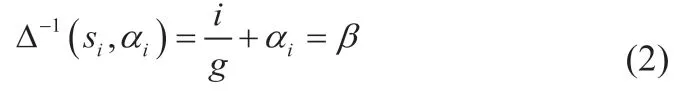
1.3 定义3

若i=j，则若，则；若则；若，则

1.4 定义4

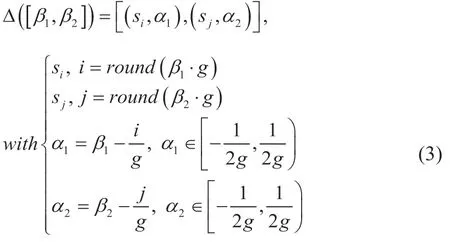
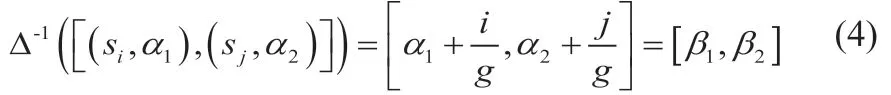
特别地，当si=sj且区间二元语义退化为二元语义组。

决策者由于信息不充足、问题复杂而不能精确评估时，二元语义难以刻画决策者真实偏好的问题，区间二元语义很好地解决了上述问题，既保全了评估信息，也为决策者降低了评估难度。

1.5 定义5

1.6 定义6

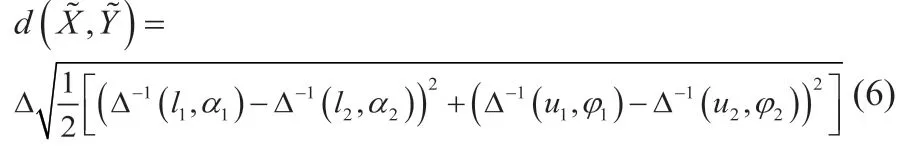
2 动态加权与区间二元语义结合的FMEA方法

本节中，我们提出一种将动态加权与区间二元语义结合的FMEA方法。考虑某个项目，有p个FMEA团队成员TMk（k=1,2,…,p）对该项目下m个故障模式FMi（i=1,2,…,m）的n个风险因子RFj（i=1,2,…,n）进行评估。风险因子的相对权重为为第k个FMEA成员给出的风险评估语义矩阵，其中akij为TMk关于FMi在RFj下的语言评估。此外，FMEA成员可以使用自己的语义集来表述自己的评估。

本文提出的FMEA过程如下：

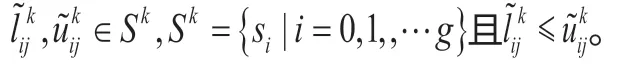
语义矩阵转换成区间二元语义矩阵的转化采用Liu等[12]中的规则。

步骤二：计算动态权值。首先计算每个FMEA成员关于FMi在风险因子RFj上与其余成员所给信息的距离之和的倒数则TMk关于FMi在风险因子RFj的权重：

该方法思想为：FMi在某个决策上与其他成员的决策信息越接近，在综合决策信息上占有比重就越大，反之则小。由此可知，FMEA成员在每个故障模式在不同风险因子上所作评估的权重是动态变化的。因为FMEA成员多为跨职能、跨学科组成，各成员在对特定故障模式的各风险因子评估的准确度、可信度是不稳定的，且FMEA成员很难做到所有故障模式有同等的把握度，故本文认为FMEA成员的权重应该随故障模式和风险因子而动态变化。

步骤三：集结每个FMEA成员的二元语义矩阵，得到集结矩阵

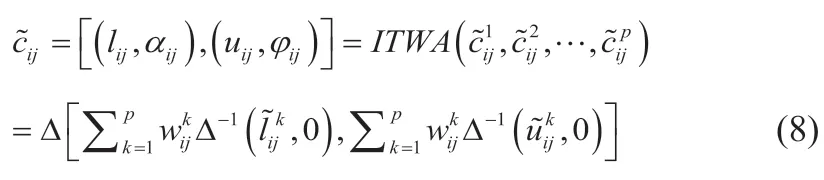
步骤五：确定参考二元语义组。传统FMEA中，RPN值越大，代表风险越高。我们希望风险达到最低，则故障模式的语言评估应该为最低层次。以区间二元语义矩阵表示的FMEA风险信息，选用最小的二元语义变量(s0,0)作为参考值是合理的[12]。因此，设定参考二元语义组：

步骤六：计算综合距离矩阵。各故障模式与参考二元语义组的综合距离公式：

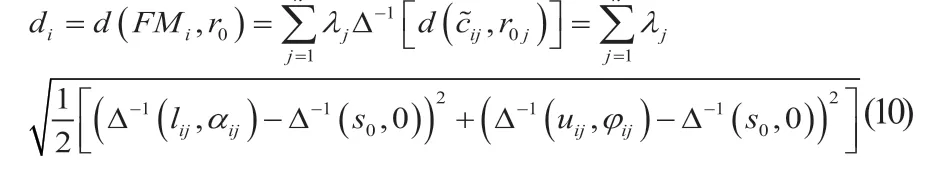
步骤七：确定故障模式风险排序。越接近最低风险的故障模式风险越低，FMi（i=1,2,…,m）的风险大小可由di（i=1,2,…,m）由大到小排序。

3 实例分析

引用Liu等[12]中的C型臂X光机操作流程中的FMEA分析案例。由5名专家TMk（k=1,2,…,5）组成的FMEA团队对C型臂X光机使用过程中的8种主要故障模式FMi（i=1,2,…,8）进行了O、S、D值的评估，O、S、D的相对权重分别为0.3626、0.4179、0.2198。5名成员各自采用了不同粒度的语义集，如表1所示。

表1 FMEA成员评估语义集

5名成员对8个故障模式的语义评估结果，见表2。

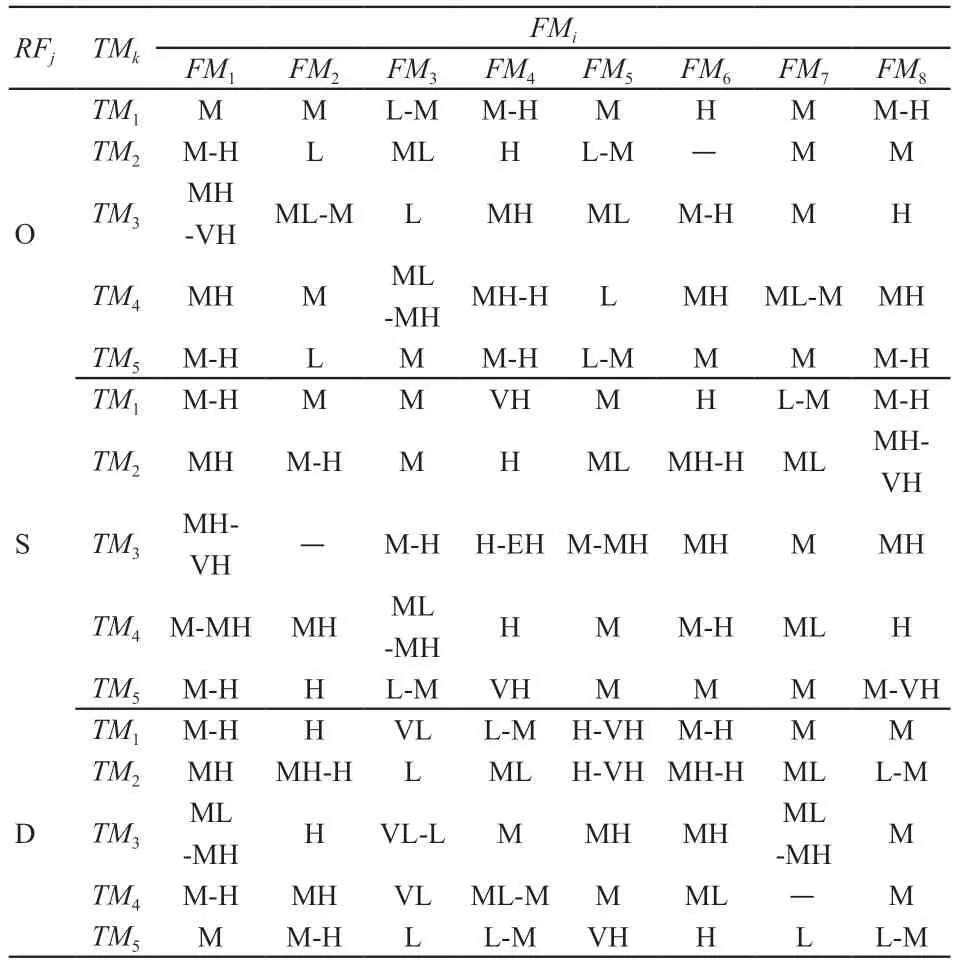
表2 故障模式语义评估结果

基于动态加权与区间二元语义结合的FMEA步骤如下：

步骤一：区间二元语义矩阵转化，结果如表3。

表3 故障模式二元语义评估

步骤二：动态权值计算。利用公式(7)计算成员动态权重，结果见表4。

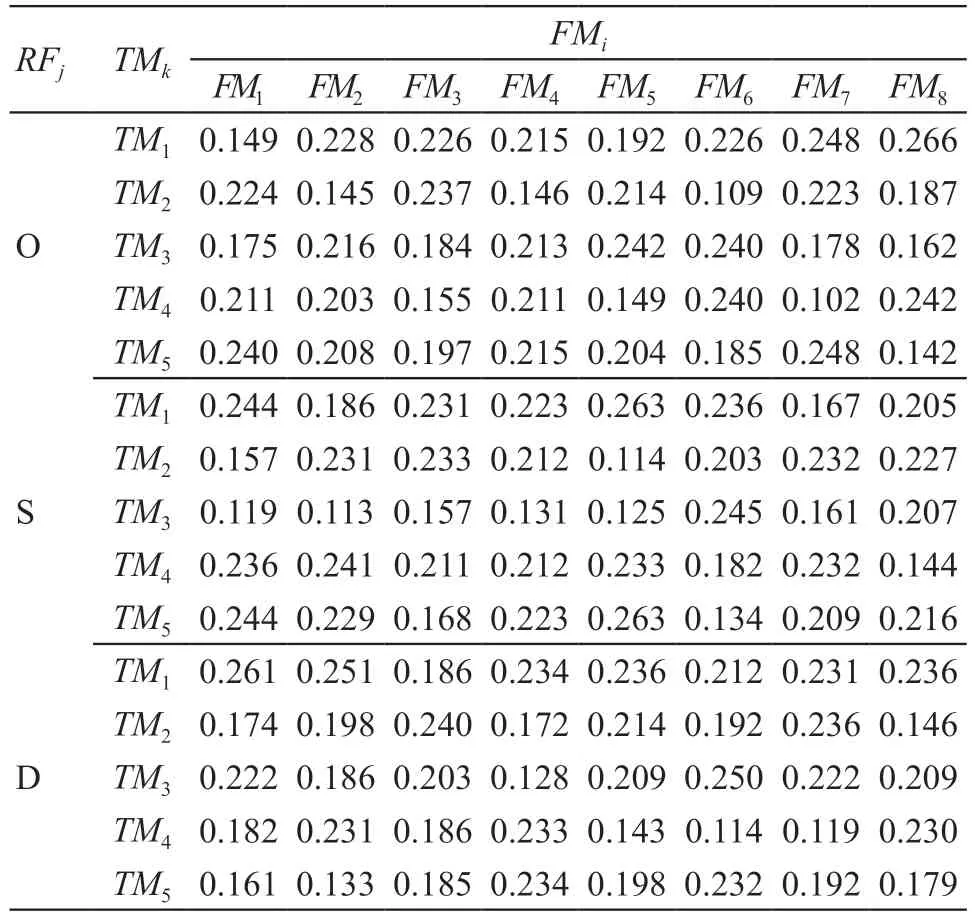
表4 FMEA成员动态权重

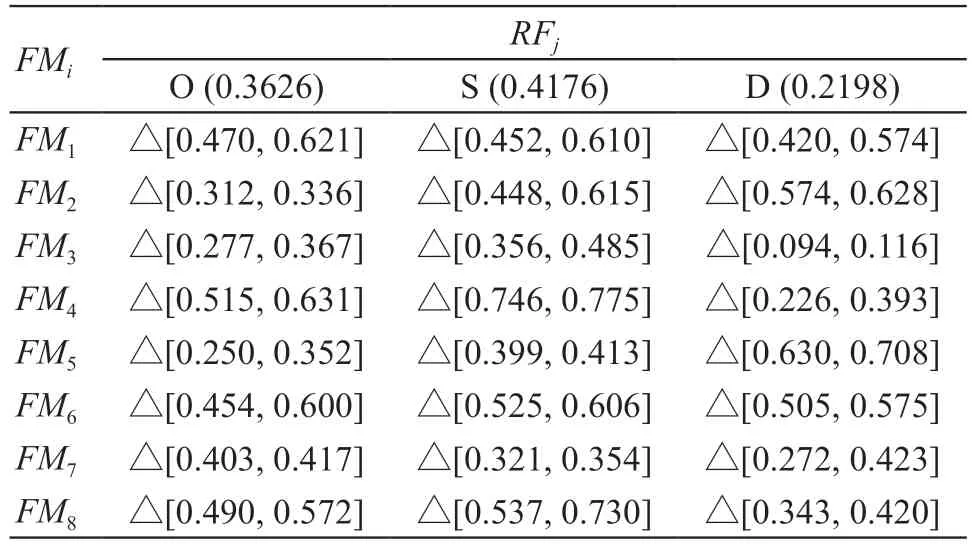
表5 综合区间二元语义矩阵和风险因素相对权重

步骤四：确定风险因子的相对权重。风险因子由FMEA团队通过最大偏差法、Delphi法、层次分析法[18]等方法确定，这里引用Liu[12]为O、S、D相对权重分别赋值为0.3626、0.4176、0.2198，见表5。

步骤六：计算二元语义综合距离。由公式(10)获得各故障模式二元语义综合距离，见表6。

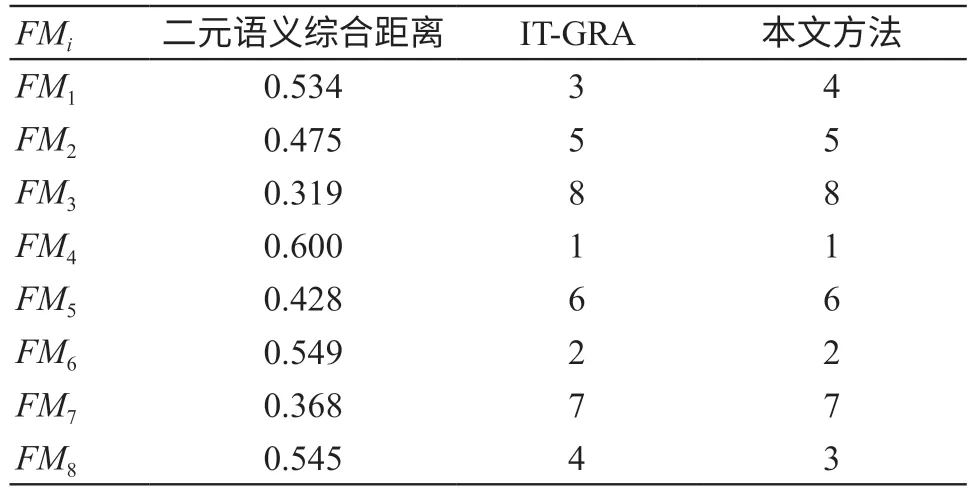
表6 故障模式二元语义综合距离及风险顺序

步骤七：根据综合距离由大到小对故障模式排序，见表6。由表6可知，故障模式风险排序为FM4＞FM6＞FM8＞FM1＞FM2＞FM5＞FM7＞FM3。

4 讨论

采用Liu等[12]的区间二元语义与灰色关联分析结合（Interval 2-Tuple and Gray Relational Analysis，IT-GRA）的方法排序结果如表6所示。两种方法得出最高风险模式均为FM4，本文与IT-GRA方法对FM8、FM1的排序不同，但均在3～4名内。IT-GRA方法在获得故障模式的综合区间二元语义评估矩阵后对O、S、D进行了与参考二元语义组的灰色关联度分析，通过对综合关联度的逆排序获得故障模式的风险优先排序。本文则直接通过计算故障模式与参考二元语义组的综合加权距离进行排序，在高风险模式和低风险模式识别中与IT-GRA结果一致同时，可以节省一些计算过程。

针对传统FMEA存在的不足，通常FMEA的改进都涉及了FMEA成员之间权重的处理，权重的确定一般根据FMEA成员的经验直接确定[19-21]，但这种处理方法存在主观问题，且权值的设定均为固定的实数，对于跨职能、跨学科的FMEA团队，成员之间对故障的风险评估的相对权威性往往存在差异。本文在集结成员评估信息之前，基于FMEA成员关于每个故障模式的风险因素的评估信息，考虑评估信息的总体一致性及个别成员的风险偏好，引入动态权值，为FMEA成员在不同故障模式不同风险因素赋予了相应的权值，保证了评估结果的共识性，避免个别成员评估信息过度影响最终决策结果，使得评估过程更符合实际情况。特别地，当只考虑FMEA成员在不同风险因子上分别赋予一个权值时，成员权值的计算方法可以同样可以采用本文的算法，从而简化其中某些计算过程。

FMEA作为最重要的风险评估工具之一，在不同的行业和组织中得到了广泛的应用。为了更精确地评估各种失效模式，本文提出的动态加权和区间二元语义结合的FMEA方法，考虑了风险因子的相对权重的同时，动态计算了FMEA成员之间的相对权重，并且使用区间二元语义为跨学科、跨职能的FMEA成员提供了灵活的多粒度语言评估方法，充分捕捉了FMEA成员的多样性评估信息，而不产生任何的信息丢失。同时，区间二元语义对自然语言的处理能力为风险评估提供了比传统方法更有效的处理方法，在故障数据缺乏，存在主观干扰的评估决策过程中，语言评估有效降低了评估难度。由于故障风险信息难以精确评估，用区间代替精确数值更具有可操作性，有效降低了决策过程中的评估难度。动态加权方法允许在个别FMEA成员对某个故障模式评估缺席的情况下，赋予其余FMEA成员新的相对权重。另外，不同于传统RPN的计算方式，本文采用区间二元语义综合距离对故障模式进行风险排序，使得RPN的处理更加精确。最后，通过C型臂X光机的案例对本文方法进行了应用演示，证实了方法的可行性、有效性。

本文对FMEA成员的权重进行了计算方法的改进，基于成员给出的评估信息与团队整体的评估信息的偏差确定其权值，可以保证评估信息达成较好的一致性，但对实际评估信息依赖程度较大，即数据驱动的方法，而未考虑FMEA成员的经验和专业知识。对FMEA成员的权重确定还需进一步改进，考虑主观权重与客观权重，既考虑FMEA成员实际情况，又能利用实际的评估信息，作为后续的研究方向。