基于密集连接结构的超分辨精简网络

高 飞，雷 涛，刘显源，陈良红，蒋 平

(1.中国科学院 光电技术研究所，四川 成都 610209；2.中国科学院大学，北京 100049；3.中国人民解放军63870部队，陕西 西安 714200)

引言

单帧图像超分辨率重建是指从一幅低分辨率图像中恢复出高分辨率图像的过程[1]。Dong在模型超分辨率卷积神经网络(super resolution convolutional neural network ，SRCNN)[2-3]中第一次将深度卷积网络的方法引入单帧图像超分辨率重建中，在重建精度方面较传统方法取得了较大提升，随之各种基于深度卷积网络的方法被提出，极大提高了单帧图像超分辨率重建的精度。过去的几年间，单帧图像超分辨重建取得了令人瞩目的效果。在基于深度卷积网络提出之前，基于样例学习的方法发展迅猛并在当时取得了最好的效果。基于样例学习的方法通过学习一个低分辨率图像块到高分辨率图像块的字典来将低分辨率空间和高分辨率空间联系起来。Freeman[6]直接通过图像对学习低/高分辨率字典，并用输入低分辨率图像块的最近邻来恢复高分辨率图像块。Chang[7]等人用流形嵌入技术取代最近邻法。Yang[8-9]将图像的稀疏性先验引入重建过程，用稀疏编码取代了最近邻法。Zeyde[10-11]用K-SVD法来表示图像块。Timofte[12]提出一种锚点近邻回归法并在当时取得了最好的效果。

深度学习的发展逐渐使超分辨取得了更好的重建表现。Dong C[2]提出SRCNN模型后，又提出一种快速超分辨率卷积神经网络(fast super resolution convolutional neural network，FSRCNN)模型[13], 通过使用更多的卷积层和在输出之前加入反卷积层，在重建速度和重建精度上都取得了很大的提升。Shi W[14]提出一种叫做亚像素卷积层的新型层，加入了这种卷积层的新模型ESPCN在当时取得了最好的效果。Huang G[15]提出的密集连接网络结构在许多计算机视觉任务上取得了很好的效果。Tai Y[16]首次将密集连接结构引入到超分辨任务中。Lim B[17]将残差学习引入到超分辨任务中。Zhang Y[18]在密集残差网络中将密集连接结构和残差学习结合在一起。密集残差网络的成功证明了密集连接结构在超分辨率重建任务中的强大作用。基于深度卷积网络的方法使得超分辨率重建的精度不断提高。

然而，这些方法良好的表现通常是以巨大的参数量和计算量为代价的，随着复原精度不断提升，模型规模也变得越来越巨大。模型参数的增加导致基于深度学习的重建算法需要大量的存储空间，使得这些实验室环境中表现良好的算法很难应用到一些存储受限的应用环境，如移动端系统。例如，目前重建精度最高的算法密集残差网络[4]，含有20个密集残差块的模型有接近6×106个参数，这种规模的参数量在许多实际应用场景中是很不切实际的。本文的工作主要集中于如何在不明显降低重建精度的前提下减小模型的规模。

通过(1)式可知，对于一个卷积层，其参数量为

P(d)=Cinput×k2×Coutput

(1)

其中：Cinput是卷积层的输入特征图的通道数；k是卷积层的卷积核尺寸；Coutput是卷积层的卷积核数量。由(1)式可以看到，有3种途径可以减少一个模型的规模：减少输入特征图的通道数；减少卷积核的数量；减小卷积核的尺寸。本文提出了两种方法以减少卷积核的数量和减少输入特征图的通道数：

1) 卷积层之间的密集连接可以充分利用每层计算得到的特征图，这样就允许网络在每层中计算更少的特征图的同时不减少复原的精度。

2) 在每个卷积层之前加入一个1×1的卷积层作为特征选择器来减少输入特征图的通道数。

实验结果表明我们的方法在模型大小和重建精度之间取得了更好的平衡。

1 密集精简网络

1.1 密集连接结构

在传统的前馈神经网络中，所有隐藏层只是将前一层的输出作为自己的输入：

Hd=Fd[Hd-1],d=1, 2, 3,…

(2)

其中：Hd是第d层的输出；Fd是第d层的转移函数；Hd-1是第d-1层的输出。这种简单的前馈结构在应用到超分辨率重建任务的时候存在如下问题：1) 在复原高分辨率图像的时候只能基于最后一层的输入，这一层的特征只有具有大感知野的信息，而缺少小感知野的细节信息。但是不同于高级的图像处理任务，重建高分辨率图像这种像素级的任务需要同时参考大感知野与小感知野的特征。2) 假设每个卷积层有C个通道，一共有D层，那么计算时得到了C×D个特征图，但是在重建的时候只有C个特征图得到了利用。3) 所有的特征图通道之间都是有冗余的，而前馈网络结构无法处理这种冗余性。

密集连接结构如(3)式：

HD=FD[H0,H1,H2,…,HD-1]

D=1, 2, 3,…

(3)

其中：Hi是第i层的输出；FD是第D层的转移函数。每个层的输出是之前所有层输出的函数，图1展示了密集连接结构的组织形式。在重建高分辨率图像的时候所有的特征图都是有用的，因此具有不同感知野的特征都被考虑到了。从图1可以看到，所有的卷积层的结果对整个特征图都有贡献，所以可以在每个层中使用更少的通道数而不必担心影响最后的复原过程。总之，密集连接结构可以充分利用已有的特征图，因此在每个卷积层中允许我们得到更少的卷积层。

图1 8层的密集连接结构示意图，所有的特征对最后一层都是有用的Fig.1 8-layer dense connection structure diagram, all features are useful for the last layer

1.2 1×1卷积层

利用密集连接结构允许我们使用更少的输出通道数，但是从图1可以看出，随着网络深度的增加，卷积层的输入通道数迅速的增长。但是在密集连接结构的深层特征图之间，常常是存在冗余的。为了说明这种冗余性，我们可视化了本文算法中密集连接结构最后一层将所有已有特征结合在一起得到的特征图，结果如图2所示。

图2 密集连接结构最后一层输入特征图可视化Fig.2 Visualization of the last input feature map of densely connected structure

可以看到，最后一个密集连接层的特征图之间存在很多的相似性。利用这样的信息进一步提取信息必然会损耗计算能力和浪费宝贵的存储空间，为克服这种冗余性，引入1×1卷积层对特征图进行选择和组合，以输入特征图某个位置的像素I(i,j)为中心的卷积运算过程如(4)式所示：

(4)

其中:I′(x,y)表示卷积操作的输出像素;I(x,y,c)表示x,y位置、第c个通道的输入像素;k(i,j,c)表示卷积核i,j位置、第c个通道的权重;2k+1是卷积核的大小，1×1的卷积核即k=0的情况。

由(1)式和(4)式可知，在输入输出通道数相同的时候，1×1的卷积层只有3×3卷积层参数量和计算量的九分之一，所以可在每个3×3的卷积层之前加入一个1×1的卷积层，以抑制特征图的冗余性并减少模型计算量。对图2得到的特征图利用9个1×1的卷积核组成的卷积层进行卷积运算，得到9个特征图，其可视化结果如图3所示。

对比图2、图3可以发现，1×1卷积层处理之后的特征图几乎涵盖了处理之前的所有模式，几乎没有丢失宝贵信息，完全可以用图3的特征图代替图2进行进一步的特征变换。

在普通的前馈网络中使用1×1卷积来减少特征图的通道数会形成信息瓶颈，但是对于密集连接结构来说，信息可以直接传递到之后所有的层中，所以在密集连接网络中，使用1×1卷积来减少模型的参数量是一个合理的思路。

图3 1×1卷积层的处理结果Fig.3 1×1 convolutional layer processing results

1.3 网络结构与通道数

最终设计的网络结构直接将低分辨率的图像作为输入，并在最后一层使用反卷积层进行上采样得到最终的高分辨率图像，直接在低分辨空间进行操作可以进一步减小计算量。最终形成的模型架构如图4所示。从图4中可以看到，3×3卷积的输入输出通道对模型的大小有很大的影响。

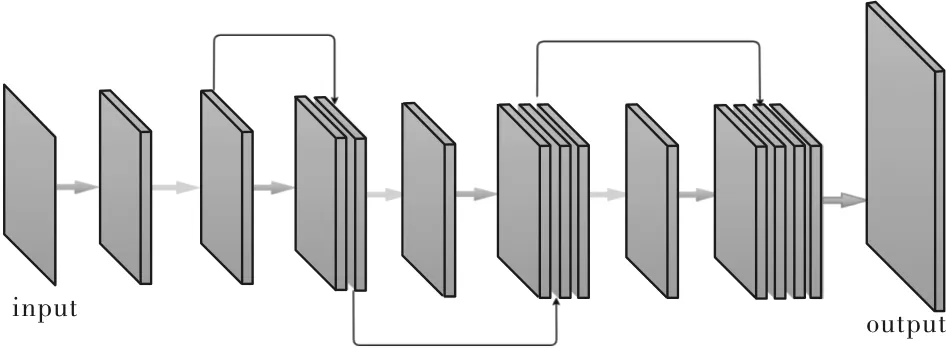
图4 密集精简网络结构Fig.4 Dense simplified network structure

在实验中，我们分别设置每层的输入通道数为3、6、9来分析通道数对模型大小与重建精度的影响。作为对比，我们去除密集连接结构中的两个1×1的卷积层，得到一种只有密集连接结构的网络，在下文简称FSRCNN-dense。

对于卷积神经网络模型，模型的参数量主要由(5)式决定：

(5)

其中:S(net)表示某个网络的参数量;h代表网络的层数;P(i)表示第i层的参数量，其计算方式如(1)式所示，取决于卷积层的输入、输出通道数和卷积核的尺寸。对于以低分辨率图像作为输入的卷积网络，每个像素上的计算量等于模型的参数量，对于将上采样图像作为输入的卷积网络，每个像素上的计算量等于模型的参数量乘以上采样倍数的平方。

图5展示了不同模型的参数量与低分辨率图像中每个像素上计算量的大小。

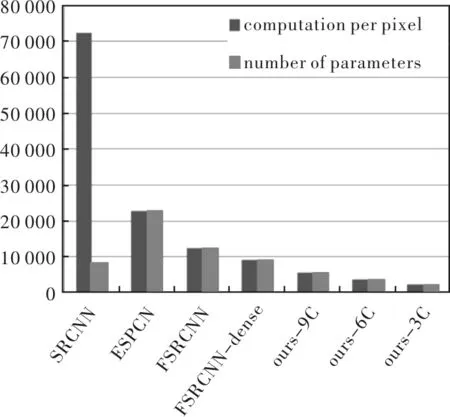
图5 不同模型的参数量和计算量对比Fig.5 Comparison of parameter quantities and calculations of different models

从图5中可以看到，仅加入密集连接结构的网络FSRCNN-dense的参数量和计算量只比FSRCNN网络略少，但是加入1×1卷积后，网络的参数量和计算量明显的下降，这一点在之后的实验结果中还有体现。

2 实验结果与数据分析

将本文提出的算法与其他3种基于深度卷积网络的方法和其他基于学习的算法进行对比。3种基于深度卷积网络的方法主要有SRCNN[2]、FSRCNN[13]、ESPCN[14]3种，选择这三种算法的主要原因是其都是模型参数量小于30 000的小型模型，其他基于深度卷积网络的算法虽然复原精度较高但是模型的参数量太大与本文算法没有可比性。本节与基于深度卷积网络算法的对比方面主要是重建精度和速度，而与其他基于学习方法的对比主要是在重建速度上。所有的基于深度卷积网络的模型都是在[5]中的一个包含91张图片上进行训练的。

2.1 与基于深度卷积网络的算法对比

为了对比算法的重建速度，在Set5上对5张图片分别进行1 000次放大3倍的操作，记录不同模型需要的时间。最终每个模型需要的时间和复原的精度如表1和图6所示。基于caffe的matlab接口进行运行时间测试，为了便于测量对比，matcaffe选用CPU模式。

从表1和图6中可以看到，没有加入1×1卷积的网络FSRCNN-dense虽然在计算速度上略快于FSRCNN网络，但是其精度损失比较大，加入1×1卷积之后的密集精简网络相对于其他对比网络有明显的速度提升，而且输入通道数为3、6、9的版本都取得了与其他对比网络相当的精度，这也验证了1×1卷积层的有效性，不仅能减小模型的计算量和参数量，而且通过特征选择可以去除无关信息，提高复原精度。

表1 对Set5每张图片放大3倍1 000次需要的时间对比

图6 不同模型的在Set5上的运行时间和重建精度对比Fig.6 Comparison of running time and reconstruction accuracy of Set5 on different models

2.2 与其他基于学习的算法的对比

将本文算法与目前广泛应用的基于样例学习的算法进行了对比，基于学习算法的精度主要来自[2]，表2展示了本文算法与其他基于样例学习的算法在Set5上复原精度的对比。

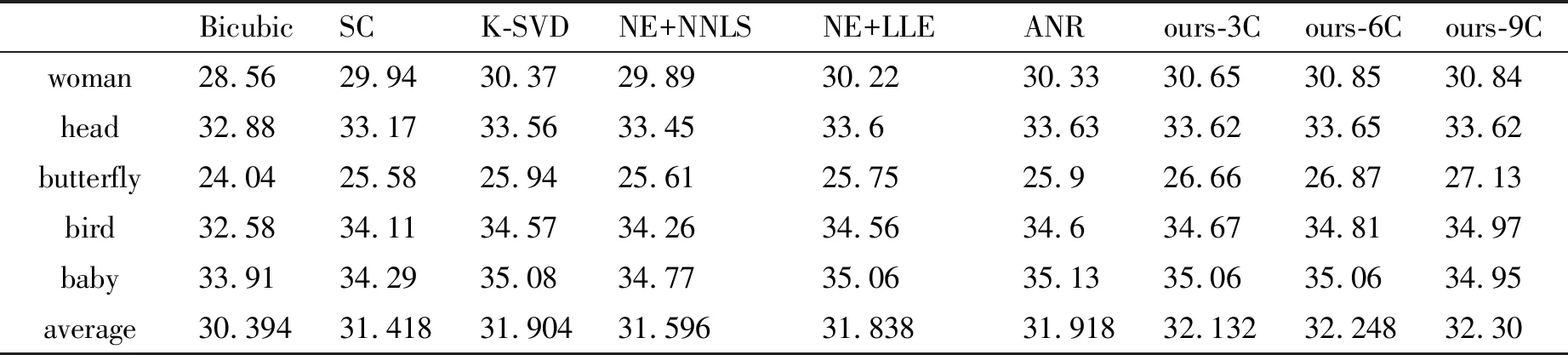
表2 本文算法与其他基于样例学习的算法重建精度对比

从表2中可以看出，即使是最小的3通道的模型，在复原精度上也是好于基于样例学习的算法的。

2.3 模型通道的影响与效果展示

表1中显示，随着通道数的增加，图像的重建时间明显增加。通道数从3到6的精度增加高于从6到9的精度增加，这可能是因为3通道的模型每层中得到的特征图不能为重建高分辨率图像提供足够的信息。虽然6通道模型在重建精度和重建速度上达到了更好的平衡，但是3通道的模型具有更少的参数，需要更少的内存并拥有更快的运行速度，这在某些应用场景下可能是更加重要的。图7展示了本文算法在某些自然图像上的重建效果。

与其他基于深度卷积网络的方法相比，本文提出的密集精简网络利用更小的模型和更少的计算量达到了相同的重建精度。同时密集精简网络的重建效果好于其他基于样例学习的算法。本文提出的算法在内存受限的应用环境下具有一定的应用价值。

图7 密集精简网络在自然图像上的重建效果Fig.7 Reconstruction effect of dense simplified network on natural images

图7是对自然图像放大3倍的效果，可以看到，相比三次内插放大，本文算法得到的结果轮廓清晰，有助于进一步图像处理任务如小目标检测等的进行。

3 结论

本文以密集连接结构作为主要结构，设计了一种密集精简网络。密集连接结构使得模型内部的梯度传递更加的流畅，这使得在模型设计中可以使用更少的通道数并采用1×1卷积层来减少模型的参数量。实验结果证明本文提出的密集精简网络在模型的大小和超分辨率重建的精度之间实现了更好的权衡。