壁面润湿性对原油携水流动特性的影响分析

王家卫，章友洪，岳晓军，张 旭，梁 敏，彭素芹，代 文

(1.中国石油长庆油田分公司 第十采油厂，甘肃 庆阳 745000； 2.中国石油新疆油田分公司 采油一厂,新疆 克拉玛依 834000； 3.中国石油新疆油田分公司 陆梁油田作业区，新疆 克拉玛依 834000； 4.中国石油玉门油田分公司 酒东采油厂，甘肃 酒泉 735000；5.中国石油华北油田分公司 第二采油厂，河北 廊坊 065700；6.中海石油(中国)有限公司 深圳分公司，广东 深圳 518000)

引 言

原油集输管道中常有油田采出水存在，因此原油管道内的流动以油水两相流为主。针对油水两相流的流型、持液率、流场变化等流动特征，国内外学者进行了较为深入的研究[1-4]。输油管道由于受地形起伏的影响，常由水平段、上升段和下降段组成，并以弯头相连接。相对于直管段，起伏地形的原油集输管道内的油水流动受到的关注较少[5-6]。由于油田采出水的密度较高，水往往会沉积于管道底部，尤其是在管道停输期间，采出水会在管道的低洼处积聚，从而引发管道的腐蚀失效。利用原油流动过程中产生的携水效应，将积水携带出管道底部，是避免内部腐蚀的一种简单而有效的方法[7-8]。到目前为止，只有少数几项研究涉及从原油管道低洼处的携水流动。

本文利用数值模拟的方法研究了原油集输管道低洼处的原油携水流动的动力学过程和界面形态，建立了原油携水流动模型，采用基于VOF模型的InterFoam求解器来求解油水界面的动力学方程，对比验证了相同条件下的实验数据和数值模拟结果，分析了原油流速和壁面润湿性对原油携水能力的影响趋势。

1 原油携水流动模型

为模拟分析原油携水流动过程，建立了原油携水流动模型，采用了OpenFOAM软件对携水过程的流动状态进行数值模拟分析；为捕捉油水界面的流动状态和界面形状，使用了基于VOF模型的InterFoam求解器来求解油水界面的动力学方程。

1.1 控制方程

在本文建立的模型中，将原油和水作为一种混合流体，同时为了在计算过程中对二者进行区别，在每一个计算网格内定义一个体积分数α(0<α<1)对油相和水相进行识别区分，由此可以得到Navier-Stokes方程的表达式[9]为：

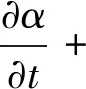
(1)

式中：t为时间，s；u为流体速度，m/s；Ur为界面压缩速度，m/s。

连续性方程和动量方程分别为：

(2)

(3)

式中：p为压力，Pa；ρ为混合流体的密度，kg/m3；μ为混合流体的动态黏度，N·s/m2；g为重力加速度，σ为油水界面张力系数，mN/m；n为界面法线向量；k为曲率。

1.2 几何模型和物性参数

以Xu[10]的油水界面实验装置为原型进行几何模型的建立，几何模型的相关参数以及网格划分结果如图1所示，其中的流体介质属性和相关参数见表1。

图1 三维几何模型结构及网格划分结果Tab.1 Structure and griding resuilt of 3D model of fluid media

介质ρ/(kg·m-3)μ/(mPa·s)σ/(mN·m-1)油8563.4318.33水9970.895/

2 结果与讨论

2.1 数值模拟计算结果验证

为验证本文的数值模拟研究结果的正确性，以管道末端出口处的原油携水量数据为依据，将数值模拟结果和实验结果进行对比。进行数值模拟计算时以实验条件为初始计算条件(积液量Vw分别为15、25、40 mL；壁面条件为疏水性壁面，接触角θ=120°)。计算结果如图2所示。

图2 不同原油流速条件下管道出口原油携水量Fig.2 Water carrying capacity of crude oil at outlet of pipeline under different crude oil flow velocity

从图2可以看出，在不同管道积液量的条件下，数值模拟和室内实验研究一致预测了引发原油携水效应的最低原油流速Uos=0.8 m/s，并且原油流速对管道出口携水量的影响的实验值和模拟值均具有较好的吻合性。因此，说明本文所选取的数学模型和所采取的数值模拟的方法能对原油的携水流动进行较为准确的模拟研究。

2.2 管道底部积水状态分析

在进行管道内原油携水流动模拟分析时，需要确定管道底部积水形态。因此，为确定油水界面在静止足够长的时间后的形态，在原油流速Uos=0的条件下进行了不同管壁润湿性(接触角θ不同)和不同积水体积条件下的油水界面形状的数值模拟。在当前条件下，油水界面上受到的作用力仅有重力和油水界面张力，从图3和图4中可以发现：随着时间的推移，积液横截面松弛为端面形状，而端面形状仅是水体积和壁面润湿性的函数。同时，当模拟亲水性表面时(接触角θ<90°)，积水会沿管道径向扩散；而在疏水性表面的条件下(接触角θ>90°)，积水会聚集形成水团[11]。

图3 不同壁面润湿性对积液形态的影响Fig.3 Influence of wall wettability on morphology of liquid accumulated in pipeline

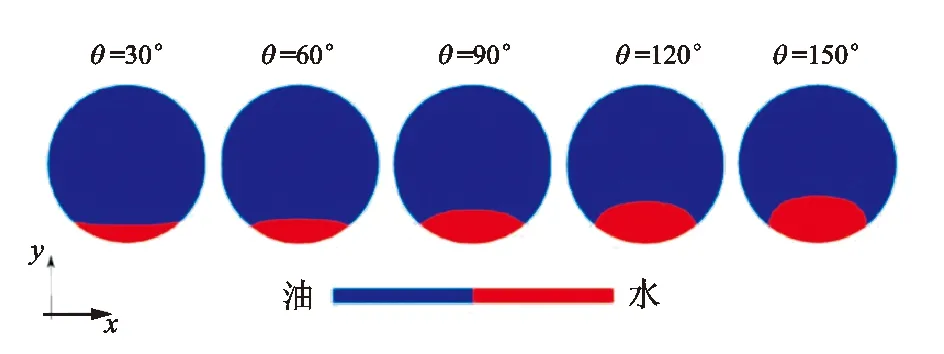
图4 不同壁面润湿性条件下积液的横截面Fig.4 Cross-section shape of liquid accumulated in pipeline under different wall wettability conditions

2.3 原油流速对原油携水量的影响

不同流速条件下管道出口原油携水量随时间的变化情况如图5所示。

图5 不同流速条件下管道出口原油携水量随时间的变化Fig.5 Water carrying capacity change of crude oil at outlet of pipeline with time under different flow velocity

从图5可以看出，在管道出口处所监测到的原油携水量随时间的变化呈现出平稳和线性的变化趋势，这表明在相同的条件下原油的携水量是保持基本恒定的。同时，由于原油流速的增加，导致原油对积水的界面剪切作用增加，进而增大了原油的携水能力，最终表现为随着流速的增加，管道出口处的原油携水量增加。

从图5(a)可以发现，当管道壁面为亲水性壁面时(θ=30°)，模拟得到原油临界流速为0.11 m/s。当原油流速Uos小于临界流速时，原油对积水的表面剪切力并不足以带动积水到达出口位置，如图6(a)所示。在水平段，随着弯头的接近，水膜的高度逐渐增大，而随着水面的上升，水膜的厚度逐渐变薄，导致没有积水跟随原油到达管道的出口位置。

当原油流速Uos超过临界流速0.11 m/s时，在原油的携水能力作用下，管道底部积液将会随原油到达管道的出口位置，并且随着时间的推移，积水不断地被带出管道。同时还可以发现，在当前条件下油水界面形状为波浪流型，如图6(b)所示。

2.4 壁面润湿性对原油携水流动的影响

当管道壁面为疏水性壁面时(θ=120°)，积水会在管道的倾斜段的入口处形成一个聚集的水团，水团在剪切作用下向上倾斜。当原油流速小于临界流速时，聚集的水团将会始终停留在倾斜管段的起始部位，如图7所示。与接触角θ=30°条件相比，聚集水团的厚度明显增加， 较厚的水团减少了管道内部的原油流动的有效水力直径，由于原油的流量是恒定的，流速将随水力直径的降低出现加速现象，从而引起较大的界面剪切，因此较低的临界原油流速就足以引发原油携水效应，如图5(b)所示，原油的临界流速为0.09 m/s。当原油流速Uos小于临界流速，并处于0.08～0.09 m/s时，只有不到5%的积水被带出。在该条件下，被带出的积水并不是由于剪切作用力的作用引起的，而是由于油水界面的波动而带出的液滴[12]。

图6 油水界面形状(θ=30°，Vw=40 mL)Fig.6 Oil-water interface shape (θ= 30 °,Vw=40 mL)

图7 油水界面形状(θ=120°，Vw=40 mL，Uos=0.07 m/s)Fig.7 Oil-water interface shape(θ=120°，Vw=40 mL，Uos=0.07 m/s)

当原油流速Uos大于临界流速时，原油的携水能力取决于壁面的润湿程度(即接触角θ的大小)，模拟结果如图8所示。从图8可以看出，当接触角θ=30°时，水以连续波状薄膜的形式存在；当接触角θ=60°时，薄膜破裂形成分散的水团，这些水团零散地分布于倾斜管壁上，并在剪切力的作用下不断向上移动；当接触角θ≥90°时，积水逐渐在倾斜管段上聚集为一团，因此在当前条件下，当原油流速足够大，所产生的剪切作用力足以携带整个管道底部积液时，就会将管道底部积液完全携出[13]。

图8 壁面润湿性对油水界面形状的影响(Vw=40 mL，Uos=0.13 m/s)Fig.8 Influence of wall wettability on oil-water interface shape (Vw=40 mL，Uos=0.13 m/s)

3 结 论

(1)本文所建立的原油携水流动模型的计算结果与实验结果对比具有较好的吻合性，能较好地模拟分析原油携水流动过程。

(2)随着原油流速的增加，原油的携水能力增加，管道内的积水更易被原油携带出管道底部，而原油临界流速的大小取决于管道壁面的润湿性。

(3)随着管道壁面的润湿程度的降低，积水有聚集为水团的趋势，与此同时原油的携水能力呈逐渐增加的趋势。