基于K-means聚类与空间相关性的零售户销售行为分析

王路遥，高 山，李 俊，樊 红

(1. 武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 441000; 2. 贵州省烟草公司贵阳市公司,贵州 贵阳 550000)

我国经济实力的增长与居民收入的不断提高，为零售市场带来了巨大的经济潜力。然而，由于零售店经营者的市场信息来源较少，导致长期以来店铺的营销工作都是一种粗放型管理[1]，以部分历史经验来把握市场规律，具有严重的滞后性。因此，当前必须将传统的以销售为中心转变成以消费者为中心，把握消费者的特征，做到高效、科学的快消品营销[2]。当前研究较多的是基于中心地理论[3]、核密度估计[4]、距离衰减理论[5]等进行的商业中心估计，如利用POI数据及零售户数据进行的区域商业中心的发掘[6]，利用空间核密度分析对汽车服务业[7]、体育门店[8]中的各类店铺进行分类聚类，发掘空间分布规律，但是都未能考虑这种聚集性与对应的营业额之间的关系，未能将空间规律与经济规律相结合[9]。基于此，本文利用零售户销售数据提取较为准确的地区消费者特征，并结合空间相关性算法，提出促进销量的空间实施方案，为更好地满足地区消费者需求，提高零售店铺利润与地区税收提供有效的指导意见。

1 数据源与预处理

1.1 数据来源

本文的主要数据源为贵阳5614个零售店铺2015—2016年逐月(共计24个月)的快消品销量和销售额数据，本文的试验选取了其中销量较高的3个类别的快消品，表示为HGSLJP、GYYHJP、GYX。其他数据为贵阳市的路网、地图数据等，为试验提供空间参考。

1.2 K-means聚类

作为经典的聚类算法之一，K-means算法是一种基于距离的聚类算法，也即通过对象之间的空间距离来评价对象之间的聚集程度[10-11]，这种空间距离也可以是其他能够表征对象间差异的特征值[12-13]。对于类别的喜爱程度或偏好程度，都与空间具有一定的关系，呈现出区域的喜好或不喜好现象。因此，笔者可以推断对于空间配比也存在一定的空间聚集性，对于那些明显呈现相同配比的区域，笔者可以认为这部分区域存在一定的类别偏好程度，并且将偏好程度映射到了当前类别销售的比例上来。选取HGSLJP、GYYHJP、GYX作为3个维度的聚类对象。对于零售户数据来说，共有5614个具有空间信息的店面，但由于小值离群点数量过多，且不同店面销量的数量级不同，如果本文将这些店面的销量取平均值作为阈值进行初步的筛选，选出优秀的店面进行聚类分析，会得到更加理想的聚类效果。

为了得到最佳的类簇数目，引入轮廓系数(silhouette coefficient)进行评价，它是聚类效果好坏的一种评价方式，取值范围在[-1,1]之间，最早由Peter J. Rousseeuw在1986年提出，轮廓系数能够用来表征聚类簇内部的聚合程度及聚类簇之间的分离程度[14]，对于一个N个点的点集，轮廓系数的计算公式为

(1)

式中,a(i)表示i向量到其所属的类簇中其他点位的平均距离；b(i)表示i向量到其他类簇中点集的平均距离。对三维销售数据进行K-means聚类，考虑轮廓系数与类间差异，最终选择3作为聚类数。

选择出合适的类数之后，进行K-means聚类，结果如图1所示，以任意两类别的横纵交点表示二者的二维聚类结果。

图中十字形符号“+”所代表的店面，3种类别的快消品销量都很优秀。三角符号“△”所代表的店面，3种类别的快消品销量一般，而圆圈符号“○”代表的店面销量较少。分别求出它们的聚类中心， 并对快消品销量采用取对处理，消除其数量级的差异，从而使发散的聚类点更加紧凑，并且同时进行对数化，结果见表1。

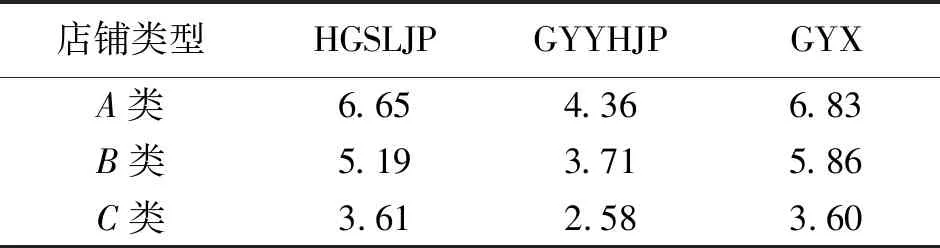
表1 取对后3类店铺各类别快消品销量聚类中心

2 试验方案与结果

2.1 聚类中心选择

快消品的配比表征了地区人口对于不同快消品的喜好程度和选择情况，不同的区域存在着较为显著的差异。那么本文所得到的配比中心对于快消品营销有无具体影响，采取合适的配比是否能够有效地提高地区销售总销量，就需要进行科学性地验证。将聚类中心与理论聚类中心的方差作为X轴，总销量作为Y轴，若呈现负相关趋势，则证明结论。

设定每个时间单元的聚类中心坐标为：(x1(i),y1(i),z1(i));(x2(i),y2(i),z2(i));(x3(i),y3(i),z3(i));每个时间单元的方差M(i)计算公式如下

M(i)=

(2)

以季度为时间单元，计算2015—2016年的各个季度月平均聚类中心，并绘制方差-销量之间的二元关系，求出最佳拟合公式，如图2所示。

为了评价拟合精度，引入拟合优度(goodness of fit)的概念，它是根据拟合方程所得到的预测值与实际观测值之间的契合程度，拟合优度越大则表示二者之间越接近。本文采用的拟合优度统计量为

(3)

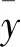
配比中心实质上表征了一个地区的人口对于不同快消品的喜爱和接受程度，将不同层次的店铺按照理论上的配比进行配货，尽可能地接近聚类中心得到的配比，可更加符合这个区域的消费者消费习惯，更加契合市场要求，能够在最大程度上提高销量的同时，又避免滞销和库存的发生。

2.2 优化方案

保持销量稳定的方式是将配比保持在理论配比中心附近，该如何具体实施是优化配置的探讨重点。由于在K-means聚类算法中，将贵阳市的店铺分成了3类，它们具有不同的聚类中心，因此，需要针对3类店铺进行分别的营销策略。对于每一类店铺，它们在自身当前的配货上，与标准聚类中心(X1,X2,X3)存在着不同的差异，部分店铺可能差异很小，部分店铺的差异可能较大。以第一类店铺(453个)为例，每个店铺与标准聚类中心都存在方差M，笔者选出M值呈现空间聚集且较小的店铺，对这些店铺进行重点调整。

为了能识别局部空间自相关，每个空间位置的局部空间自相关统计量的值都需要计算，空间位置为i的局部Moran’sI的计算公式为[15]

(4)

局部Moran指数检验的标准化统计量为

(5)

式中，E(Ii)和VAR(Ii)是其理论期望和理论方差。

局部Moran’sI的值大于数学期望，并且通过检验时，提示存在局部的正空间自相关；局部Moran’sI的值小于数学期望,提示存在局部的负空间自相关。缺点是不能区分“热点区”和“冷点区”2种不同的正空间自相关。空间自相关的热点区域一般表征变量数值较高且呈现聚集性的区域或点集，而本文的店铺方差则是方差M越小，销量越高，因此这里需要对方差作反方差的处理

(6)

式中，M表示店铺配比与标准配比中心的方差，乘以100是为了扩大反方差的数量级，便于进行自相关计算。将第一类店铺的M*作为变量进行空间自相关分析，根据自相关分析的结果来决定配比的调整策略。以店铺的季度聚类方差和季度销量为自变量和因变量建立函数关系，如图3所示。

为了提高地区总销量，将那些当前销售情况不理想的店铺进行重新的配货调整，把握地区的总体销售特征，能够有效地提高其实际利润，满足地区顾客的偏好。以第一类店铺为例，M*为自变量，进行空间自相关分析，见表2。

符号“△”表示的店铺为M*呈现“高-高”聚集最为明显的店铺，这些店铺总体上呈现出一种与理论配比中心十分接近的态势，这就代表了这部分区域的消费者偏好十分明显，就可以将这部分店铺中与标准配比差异较大的店铺进行调整，将它们的M*进行显著的增高，可以较大幅度地往理论配比中心靠拢；而符号“☆”代表的店铺则为“低-高”或“高-低”聚集的店铺，总体上与配比中心处于次级接近的态势，可以对其做出小幅度的调整；对于符号“○”表示的店铺，则为“低-低”聚集或者无规律店铺，对于这些店铺暂时不进行调整或只进行微调即可。

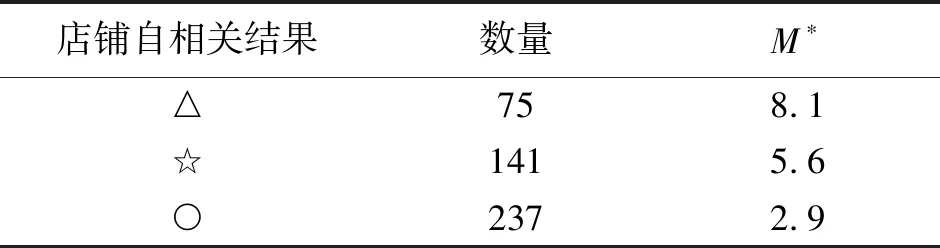
表2 自相关分类结果与各类店铺数量

表2为店铺指标，具体的调整策略分为两种，一种为保守型策略，也即将“高-高”店铺中低于M*=8.1的店铺，全部调整到M*=8.1，并基于M*来求取其理论销量，并参考理论配比进行配比，使得新配比更加接近理论配比。对“高-低”或“低-高”店铺中低于M*=5.6的，统一将M*上调至5.0～5.6之间。对于第三层则不做处理。第二种为提高型策略，“高-高”店铺的M*数值总体提高15%，“高-低”或“低-高”店铺总体提高8%，其他总体提高3%。然后基于新的M*进行销量的预测和配比。表3是保守和提高型策略对于贵阳市快消品销售店铺的销量提高情况。

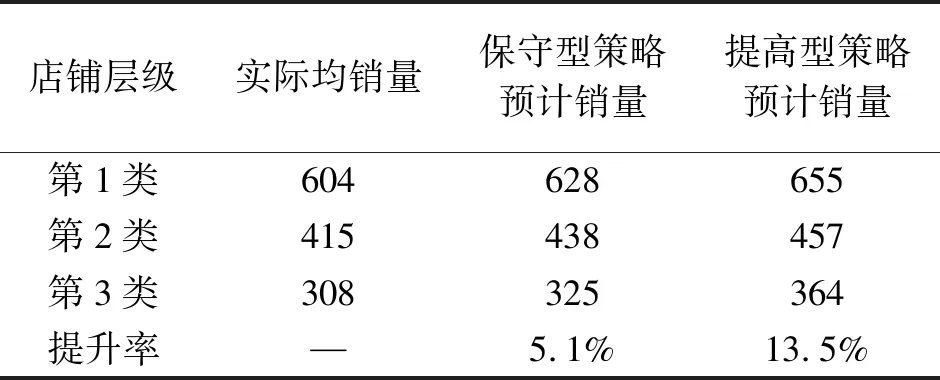
表3 不同策略对销量影响

由表3可见，即使采用保守型策略，地区总销量也提高了5.1%，只要在保守型策略上进一步求得最佳拟合率，提高M*，那么地区总销量就会取得进一步的提高。

3 结 语

传统的企业营销策略往往是控制型营销，由企业自上而下、由内及外的控制型决策过程，难以适应消费者碎片化、个性化的消费趋势，根据传统经验制定的销售策略往往具有一定的滞后性，且不易划定策略实施地区、不易确定策略实施时间。根据当前流行的营销模型，并结合GIS空间分析思想进行的研究，能够全景式地掌握市场动态，了解碎片化的消费者市场，做到有的放矢的销售策略制定，辅助企业决策者进行优化的战略制定与实施。

本文的研究能够有效地发掘地区销售特征，并推理消费者群体特征，得到了最佳产品配比方式，并论证了配比方式与总销量之间存在的正相关关系，为地区销量的提高和精准配货方案的实施提供了依据。在此基础上，结合空间相关性理念，对空间方案的部署实施提供了一种有效的施行方案，在结合店铺特征的基础上提供保守与积极型的空间优化策略，从而为店铺和配货企业提供可行性较高的方案。