人力资本结构与技术进步——异质性影响分析及其跨国经验证据

台 航 崔小勇

一、引 言

经济全球化的发展促进了世界各国之间的经济文化交流，也带动了先进技术由技术领先国家向其他国家的扩散和传播，为技术落后国家的技术追赶提供了有利条件。然而，尽管技术扩散有利于技术进步，一个国家内部的生产要素投入特别是人力资本积累在技术进步过程中仍然发挥着不可替代的作用。内生增长理论认为，人力资本是技术进步活动的主要投入要素(Nelson和 Phelps，1966；Romer，1990)，而不同类型的人力资本对技术进步的影响存在差异。那么，当人力资本总量一定时，不同类型的人力资本之间所形成的相对结构对技术进步的影响是否一样呢？由于存在性质不同的技术进步活动(技术创新和技术应用)，而这些活动所依赖的人力资本类型又并不一致，那么人力资本内部的结构性变化对技术进步的整体影响势必会存在差异。关于这个问题学者们探讨得并不多。本文将依托于理论分析和跨国经验证据，从结构性的角度出发，分别以技术创新活动和技术应用活动产生的效率变化为研究对象，重点探讨人力资本结构变化对两种效率变化所产生的异质性影响。

党的十九大报告强调：“创新是引领发展的第一动力，是建设现代化经济体系的战略支撑。”其中，人才培养是实施创新驱动战略、建设创新型国家的重要基石。更为重要的是，自 2008年全球金融危机以来，各国贸易保护主义有所抬头，国际经济发展中逆全球化现象有所显现，以技术性贸易壁垒为代表的非关税措施制约着跨国技术扩散。在此情况下，把握人力资本内部的结构性差异对技术进步尤其是技术创新活动的影响，无疑具有重要的现实意义，这将会为我们突破未来可能面临的技术封锁和为技术进步的长远发展制定具有针对性的人才培养方案提供重要的借鉴。

关于人力资本的类型，学者们通常按照受教育程度将人力资本分为熟练型和非熟练型两类，前者一般是指受过高等教育的劳动力；而本文所研究的人力资本类型更为细化，包括初等教育型、中等教育型和高等教育型三种类型。就技术进步而言，大部分研究普遍根据活动性质的不同将技术进步过程分为技术创新活动和技术模仿活动(包括技术追赶或技术扩散)。如果国家之间具有完全的开放度，则每一时点的技术前沿具有唯一性，那么技术落后国家趋向技术前沿的技术追赶活动(或者技术先进国家出现的向技术落后国家的技术扩散活动)，实际上属于技术应用范畴。因此，为了保持理论分析和实证分析的一致性，本文将技术进步活动分为技术创新和技术应用，以便于分析不同类型的人力资本所产生的异质性影响。

以往文献在研究不同类型的人力资本对技术进步的影响时，也主要以技术创新和技术模仿为研究对象来展开。这些研究通过假定技术创新和模仿活动在技能需求方面的差异来探究给定经济体在接近技术前沿的过程中不同类型的人力资本对技术进步的异质性影响。例如，Benhabib和 Spiegel(1994、2005)、Dowrik和 Rogers(2002)通过分别构建不同的技术扩散模型，发现人力资本水平的提高不仅有助于技术创新，而且还有助于技术扩散或技术追赶；然而，他们所分析的对象是整体的人力资本存量，并未对人力资本的不同类型进行区分。Vandenbussche等(2006)假设技术创新活动相对于技术模仿而言属于技能密集型，以此构建内生增长模型并结合实证分析指出，经济体越是接近技术前沿则熟练劳动力的增长效应越为显著；而当经济体远离技术前沿时，密集使用非熟练劳动力的技术模仿则是提高全要素生产率的主要动力。Messinis和Ahmed(2008)的实证分析结果则表明熟练劳动力有助于技术创新和技术扩散。Ang等(2011)以 Vandenbussche等(2006)的分析为基础并进一步扩展了样本范围，其实证分析结果表明初等教育和中等教育有利于技术模仿，而高等教育有利于技术创新；当中高收入国家接近技术前沿时，高等教育对技术进步的增长效应会逐渐增强。Basu和Mehra(2014)通过构建不同技术进步类型的内生增长模型来探讨不同类型人力资本的差异性作用，发现熟练型人力资本在“技术模仿-技术创新”型和“技术创新”型的增长体制中具有明显的增长效应，而非熟练型人力资本只在“技术模仿”型增长体制中发挥促进作用。Cerina和 Manca(2016)则进一步放松了 Vandenbussche等(2006)关于技术进步活动规模报酬不变的假定，认为经济体在接近技术前沿的过程中，贫穷国家的熟练型劳动力所产生的边际增长效应会逐渐增加，而在接近技术前沿的国家里，其作用正好相反。

回顾文献，我们发现以往的研究还存在着一些局限。首先，以往研究多分析的是人力资本对整体技术进步率的影响，而对技术模仿或创新所产生的效率变化并未展开深入研究。Vandenbussche等(2006)、Ang等(2011)、Cerina和 Manca(2016)等大部分文献主要探讨了各类型人力资本对技术进步率的差异性影响；然而，在不同发展水平的国家里，技术模仿和技术创新所产生的效率变化存在差异，那么人力资本的影响作用也会不同，关于这一点鲜有研究涉及。其次，关于人力资本结构对技术进步的影响，目前的研究文献仍缺乏系统分析。学者们多以人力资本存量为研究对象，而对于各类型人力资本及其相对结构所产生的影响是否具有差异性，他们并未深入分析。此外，在人力资本测算方面，他们单纯地使用年限法或人口占比法来衡量人力资本存量，这一做法也具有较大的片面性，因为不同类型的人力资本之间所存在的质量差异(受教育年限和教育收益率的差异)也会显著影响人力资本作用的发挥。

鉴于过去研究文献中存在的不足，本文通过借鉴以往的研究方法，以跨国经济数据(Penn World Table 9.0，PWT 9.0)和教育数据(Barro和Lee，2013)为基础，详细测算了各国初等教育型、中等教育型和高等教育型的人力资本结构占比，并利用 Malmquist指数分解法和随机前沿分析法(SFA)对各国的技术进步率进行了有效分解，即分解为技术效率变化和技术变化：前者反映了技术应用活动(或技术模仿)所产生的效率变化，而后者反映了技术创新活动所带来的纯技术水平的提高。在此基础上，本文通过使用跨国面板数据回归，分别就各类型的人力资本结构对技术效率变化和技术变化的影响作用进行了实证检验，以理清具体的作用机制。本文的主要贡献包括以下几个方面。

一是基于教育收益率而对人力资本结构进行了测度。本文以 Mincer(1974)提出的人力资本与收益率之间的关系为基础，由此测算了 136个国家 1970—2010年每隔五年的初等教育型、中等教育型和高等教育型人力资本存量，并计算了相应的人力资本结构。以往研究在测算人力资本时，并未考虑各国不同的受教育程度在教育收益率和受教育年限方面存在的跨国差异，而这些要素影响了各类型人力资本的质量。本文采取的测算方法充分考虑到不同类型的人力资本结构之间所存在着的质量差异，以精确衡量它们的经济价值。据此，本文结合跨国经济数据库形成了一个具有95个国家或地区共9期的数据面板，这为实证分析提供了详实的样本数据基础。

二是对各国的技术进步率即全要素生产率(TFP)的增长率进行了有效分解。与以往研究所不同的是，本文利用 Malmquist指数分解法和随机前沿分析法(SFA)法将TFP增长率分解为技术变化和技术效率变化两个部分，以深入研究人力资本结构对技术进步效率变化结构的影响。Vandenbussche等(2006)等一系列研究均以技术进步率(TFP增长率)为研究对象，这种分析的局限性在于，我们无法洞察人力资本结构对技术进步的影响路径。相反，通过利用Malmquist指数分解法进行效率分解，技术变化反映了因技术创新而带来的纯技术变化，技术效率变化则反映了因技术应用(或技术模仿)而带来的效率变化，两者的乘积才综合反映了技术进步率。因此，通过研究人力资本结构对技术变化和技术效率变化的差异性影响，我们将理清不同类型的人力资本结构具体通过哪种路径来影响到最后的技术进步，并且探究具体的作用机制是否存在差异，从而丰富我们对人力资本结构和技术进步之间关系的认识。

三是在技术扩散的背景下重点探讨了各国(或地区)人力资本结构对技术进步效率的影响。与以往文献不同的是，在研究人力资本与技术进步之间关系时，本文做了两个方面的重要补充：一方面，不再关注各类型人力资本存量的影响作用，而是在假设人力资本总量一定的前提下，重点探讨人力资本内部所存在的结构性差异对技术变化和技术效率变化的影响。另一方面，同时考虑了经济全球化所带来的技术扩散的影响，以更加准确地、稳健地考察人力资本结构对技术进步的影响作用。结果表明，在控制给定经济体与技术前沿距离的情况下，初等教育型的人力资本结构占比是影响技术效率变化的重要因素，高等教育型的人力资本结构占比对技术变化而言更为重要，中等教育型的人力资本结构占比对两者的影响并不明确。更为重要的是，本文通过进一步讨论发现，随着经济体不断接近技术前沿，不同类型的人力资本结构对技术效率变化和技术变化的影响呈现出边际递减的趋势。

本文余下内容安排如下：第二部分从理论上分析人力资本结构对技术进步产生的效率变化的影响机制，并提出研究假说；第三部分详述人力资本结构的测算方法和技术进步效率的分解方法；第四部分在第三部分的基础上，利用跨国面板数据实证分析人力资本结构对技术进步效率变化(技术效率变化和技术变化)的影响，并进行稳健性检验；第五部分展开进一步讨论，探讨当经济体接近技术前沿时人力资本结构的变化对技术进步的影响程度是否会发生变化；第六部分总结全文并提出政策启示。

二、研究假说

内生增长理论认为，人力资本对技术进步的影响体现在两个方面：创新知识(技术)和加速技术的吸收与扩散。首先，人力资本是知识创新和技术开发的重要源泉。Romer(1990)指出，知识(技术)由于具有非竞争性而能够产生“溢出效应”，因此任何个人所进行的知识生产都能提高整个社会的生产效率。其次，人力资本是技术应用的必要条件。在其他条件一定的情况下，人力资本的存量越大，技术吸收与扩散的速度就越快，物质资本的生产效率也就越高。技术进步主要包括两个方面：技术创新和技术应用。技术创新意味着生产可能性边界的外推，而技术应用则体现了趋向生产可能性边界的内部资源配置优化；在开放经济的条件下，技术应用还包括跨国之间的技术追赶(Kumar和 Russell，2002)。相应地，技术进步所带来的效率变化包括两部分：技术变化和技术效率变化。前者代表了技术创新水平的变化，即在投入要素不变的情况下，单纯地因为技术水平的提高而导致的效率变化；而后者代表了技术应用效率的变化，即在各期技术水平不变的情况下，单纯地因为各期要素利用效率的提高而带来的变化。

人力资本结构对技术效率变化和技术变化的影响具有差异性。一方面，根据Aghion等(1998)、Vandenbussche等(2006)等学者的分析，高等教育型人力资本往往被视为技术进步的关键投入要素。相对于技术应用而言，技术创新活动需要更多技能的投入，因而它要求人力资本具备更多的劳动技能，或者更高的教育水平。因此，高等教育型的人力资本对技术创新的影响更大。另一方面，Romer(1986、1990)、Lucas(1988)等在研究中把初等教育型和中等教育型人力资本作为直接的劳动投入来引入到生产函数当中。由此可见，初等教育型和中等教育型的人力资本可能直接作用于生产活动；而当技术水平(或生产可能性边界)给定时，两者在生产活动中发挥的作用更多地体现在促进了技术应用水平的提高，即将给定的生产技术应用到具体的生产实践中，并不断促进生产活动向生产可能性边界趋近。值得注意的是，对于中等教育型的人力资本而言，由于其既包括全日制的中学教育，也包括职业高中等技术性和职业性较强的学历教育，因此它对技术创新和技术应用都能产生影响。然而，中等教育型人力资本积累，是促进技术进步还是促进技术应用，或者说对技术创新和技术进步的相对影响如何，以往的理论研究并未给出明确结论。因此，我们需要通过实证分析来确定中等教育型人力资本的结构性变化对技术效率变化和技术变化的差异性影响。

为此，本文根据以往文献的研究成果提出如下研究假说。

假说1：由于技术应用主要受初等教育型的人力资本影响，因此初等教育型人力资本占比的提高会促进技术效率变化。

假说2：由于技术创新主要由高等教育型的人力资本决定，因此高等教育型人力资本占比的提高则会促进技术变化。

假说3：对于中等教育型的人力资本而言，其对技术变化和技术效率变化都会产生影响，但是影响性质并不明确。

综合以上假说，本文的逻辑思路如图1所示：

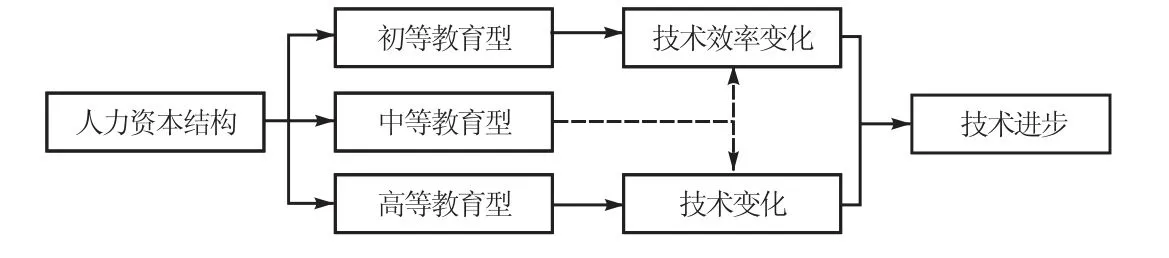
图1 人力资本结构对经济增长的影响机制

下面，本文首先提出人力资本结构的测算方法和技术进步效率变化的分解方法，然后设计实证模型对以上假说进行验证。

三、人力资本结构的测算和技术进步效率变化的分解

（一）测算人力资本结构

目前学术界主要采用收入法来测算人力资本存量，即从人力资本投资收益的角度出发，通过核算人力资本积累未来所能带来的收益现值总额来反映人力资本的投资价值。本文借鉴 Jorgenson和Fraumeni(1989、1992)、Hall和Jones(1999)、Caselli(2005)和 PWT 9.0(2016)对人力资本的测算方法，以不同受教育程度的人口占比、平均年限以及教育收益率为基础来测算初等教育型(Hp)、中等教育型(Hs)和高等教育型(Hh)的人力资本存量①以往学者在研究时通常使用受教育年限或人口占比来代表人力资本，例如 Barro和 Sala-i-Martin(1995、2003)、Barro(2001)、Vandenbussche等(2006)和Ang等(2011)。然而，这些方法忽略了人力资本所能带来的经济价值，有很强的片面性。根据 Mincer(1974)的研究，工资与教育年限之间存在对数线性关系，为此Hall和Jones(1999)、Caselli(2005)和PWT 9.0(2016)等在测算人力资本存量时均采用对数线性公式来表示人力资本存量与平均受教育年限之间的关系，但是他们并未考虑不同受教育层次的人力资本存量的测算方法；此外，Jorgenson和Fraumeni(1989、1992)等在测算时还充分考虑了年龄分组的影响，但是他们的方法以微观数据为基础，当我们使用跨国宏观数据进行测算时将面临着较大困难。。具体而言，就是以年龄分组数据为基础，分别测算各年龄组中不同受教育程度所带来的收益，并以各年龄组的不同受教育程度的人口占比为权重来进行加权平均，再综合计算不同受教育程度的人力资本存量。其中，教育收益率通过计算各年龄组给定受教育程度的收益率和平均受教育年限的自然指数值来获得。各类人力资本存量的测算公式如下所示：

各受教育水平的人力资本结构为：

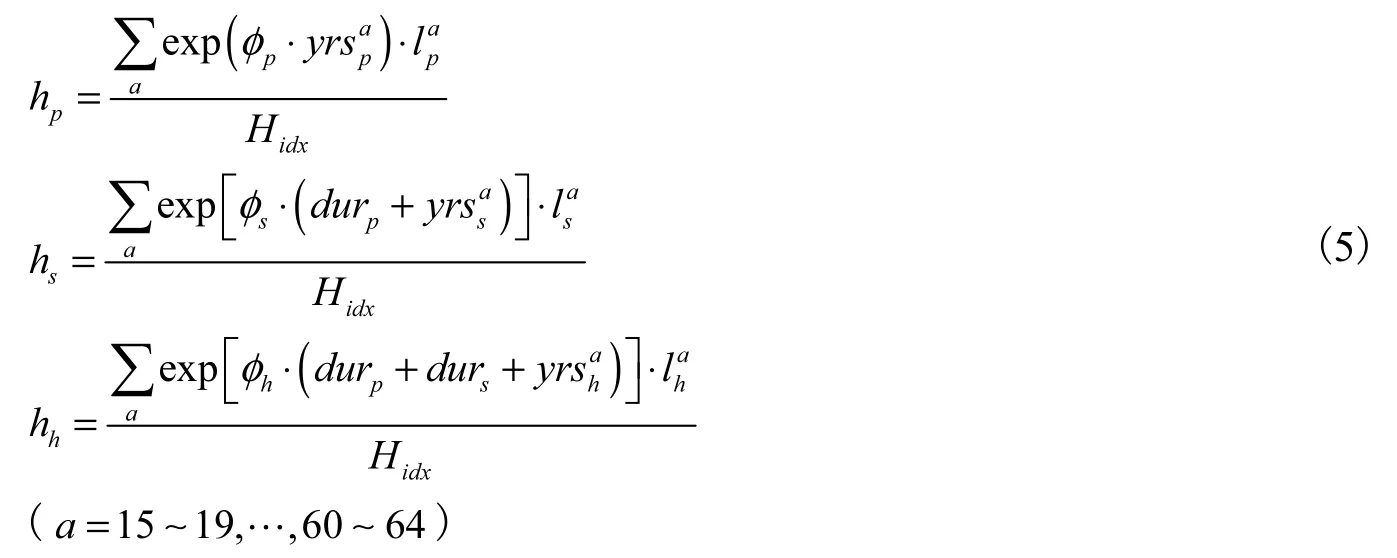
其中：

关于数据来源，教育人口占比和平均受教育年限数据来自于 Barro和 Lee(2013)提供的跨国教育面板数据集。在测算各类型的人力资本存量时，需要综合考虑各国不同教育层次的教育收益率差异和学制年限差异，本文以 Psacharopulos(1994、2004)的研究成果和联合国教科文组织(UNESCO)的数据库为基础，按照合理的方法确定各国法定学制年限和教育收益率的具体数值(法定学制年限和教育收益率的确定方法详见台航、崔小勇(2017)的文献)。

利用上述方法，本文共测算了 136个国家或地区的 1970—2010年每隔五年的初等教育型、中等教育型和高等教育型人力资本存量数据，并以此为基础计算了各国的人力资本结构。各国不同类型的人力资本存量及其结构情况如表1所示。

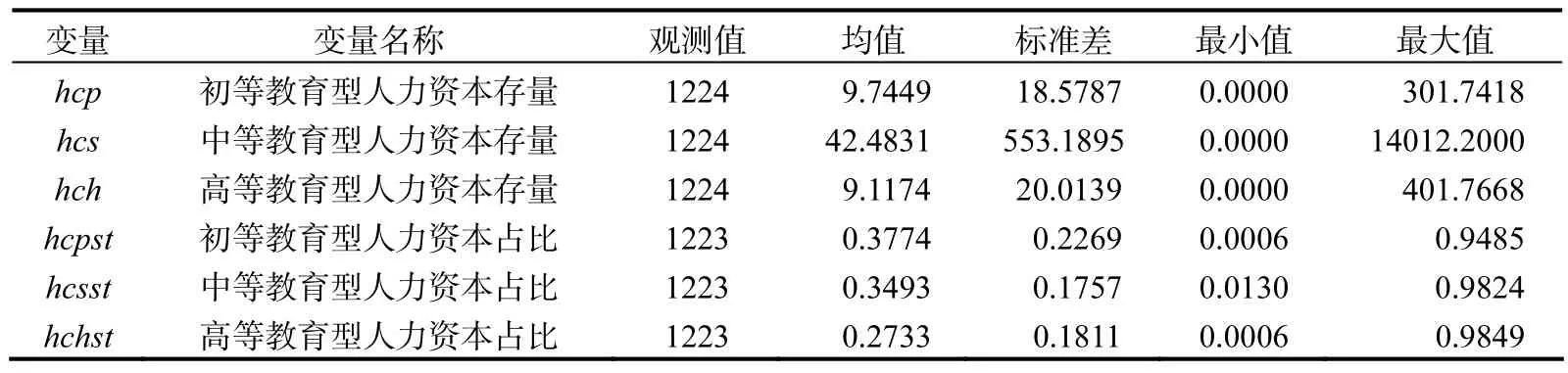
表1 各国不同类型的人力资本存量及其相对结构状况

（二）技术进步的分解

正如前文所述，技术进步所带来的效率变化包括技术变化和技术效率变化两个部分，前者代表了技术创新水平的提高，后者代表了技术应用水平的提高。本文将使用随机前沿分析法(SFA)来测算各国或地区的技术效率，并在此基础上利用 Malmquist指数分解法对技术进步所产生的效率变化进行分解。

1.技术进步的测算

技术进步主要通过测算全要素生产率(TFP)的变化率来反映；而测算 TFP变化率则需要确定各国或地区的技术前沿并计算各自偏离技术前沿的距离，即技术效率。本文利用随机前沿法(SFA)来测算技术效率。SFA测算法是在估算生产前沿函数的基础上，将偏离生产前沿的观测现象归为技术无效率，并将外部随机性因素的影响如非预期的扰动等充分考虑进来(Greene，2008)。值得注意的是，SFA法以一定的经济理论为基础，并可以使用计量经济技术进行估计；当数据噪声成为测算障碍时，它比数据包络分析法(DEA)更具优势。由于我们使用跨国数据进行分析，各国或地区的数据差异较大并且易受随机因素的干扰，因而使用SFA法测算各国的技术效率也更为合理。

根据Kumbhakar和Lovell(2000)的研究，随机前沿生产函数的一般形式为：

在式(7)～式(9)中， f(⋅)表示最优生产前沿，xit表示要素投入；vit代表测量和设定误差，假设服从正态分布；而uit则代表了技术无效率，假设服从半正态分布；而在实践中一般需要对生产函数的等式两边求对数，即：

为了便于效率分解，本文采用了形式灵活的超越对数函数进行分析(Coelli等，2005)①Coelli等(2005)指出超越对数函数具有形式灵活的特点，而且可以对任何函数形式进行二阶近似。，即：

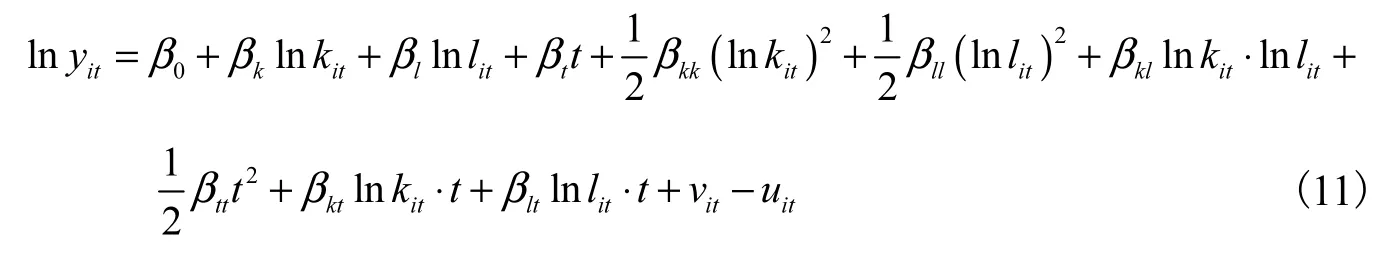
在式(11)中，下标 i表示国家，t表示时间；yit表示总产出，kit和lit分别表示资本投入和劳动投入，β表示各参数值。

对uit的估计体现了各国或地区偏离技术前沿的距离，而各国或地区的技术效率可以表示成这体现了可观测产出与相应随机前沿产出之比(Coelli等，2005)。对于给定的复合误差项 eit=vit-uit，我们可以通过求解 exp(- uit)的条件期望来对各国的技术效率进行预测(Battese和Coelli，1988；Kumbhakar和Lovell，2000)，即：

考虑到各国或地区在不同时期的TFP效率值存在差异，测算出来的效率值应当具有时变性和个体差异性。为此，我们要选择时变随机前沿模型进行分析。通常情况下随着时间的推移，技术水平会不断提高，存在的技术无效率会逐渐减少。为此，本文假定技术无效率项uit适用目前最为常用的“时间衰减”模型(Battese和 Coelli，1992)，其形式为其中，Ti为时间终点，ui为各国或地区不随时间变化的技术无效率项，η为待估参数。由此我们可以得到每期各国或地区的技术效率值。本文主要采用该模型来进行效率分析。

2.Malmquist指数分解法

在技术效率测算的基础上，本文使用Malmquist指数法对TFP的变化率进行测算和分解。根据 Malmquist指数法，TFP的变化率是在给定技术水平(或技术前沿)的前提下，通过计算各期的投入产出集①投入产出集即(x t ,yt )，其中xt和yt分别表示t期的投入要素和产出。相对于给定技术前沿的距离之比来获得的。由于各期面临的技术前沿不同，导致技术的参考期会有所不同。为了避免技术的随机选择问题，以Malmquist指数法在基期(s期)和现期(t期)的技术条件下分别测算两期的投入产出集相对于技术前沿的距离之比，然后求解两者的几何均值来得到TFP变化率，即：

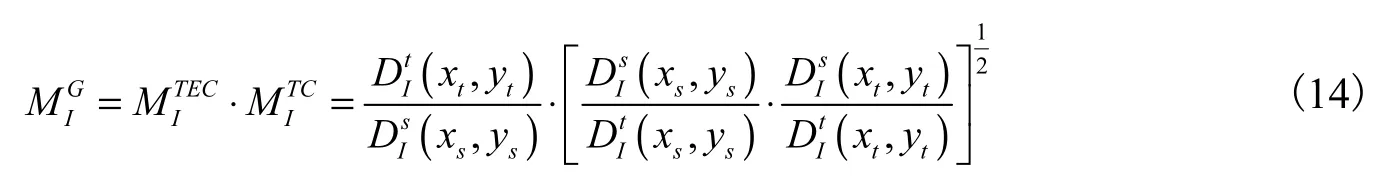
本文借鉴 Coelli等(2005)的做法，利用 SFA法的测算结果计算 TFP的变化率并进行分解。根据对uit的定义，式(12)测算的技术效率TEit就代表了式(13)和式(14)中的距离函数值。因此，对于技术效率变化指数而言，根据式(14)中的定义我们可以得出i国从s期到t期的技术效率变化指数，即：

对于技术变化指数而言，式(14)表明技术变化反映了技术前沿或生产前沿随时间的变动，在式(11)中生产前沿函数为：

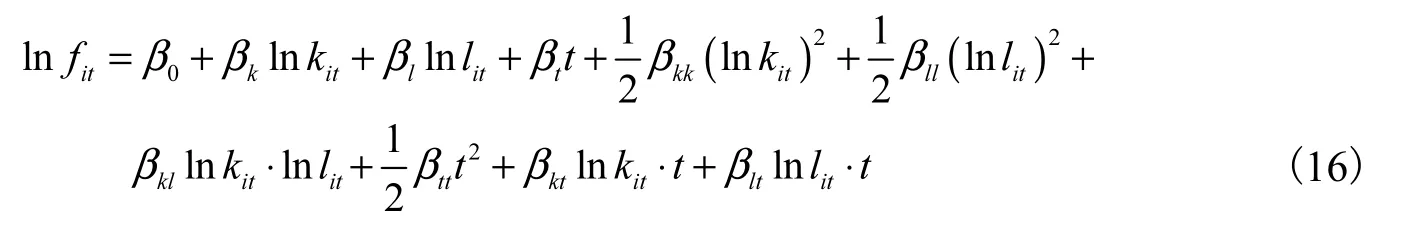
通过lnfit对时间 t求导就反映了生产前沿函数随时间的变动。为了避免投入产出集的时期选择问题，我们可以通过分别求解基期(s期)和现期(t期)的生产前沿函数对时间的偏导数，然后计算两者的几何均值，即：

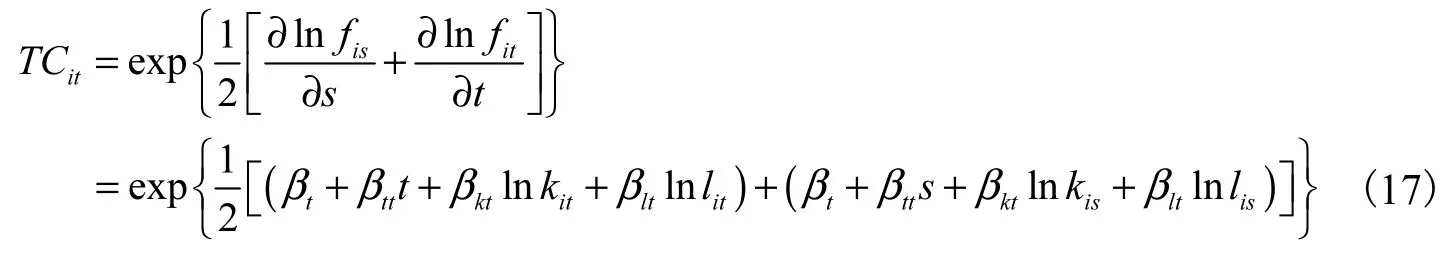
上述测算的技术效率变化和技术变化均为环比发展速度，因此综合两者并根据式(14)可得TFP的变化率为：

3.测算结果

按照文献中的普遍做法例如 PWT 9.0(2016)等，本文选取资本和劳动作为要素投入，而选取实际GDP作为产出来进行TFP增长率的测算和分解。本文使用的数据主要来自于PWT 9.0(2016)。其中：产出数据为产出导向的实际GDP(rgdpo，以链式购买力平价和2011年不变美元衡量以消除通货膨胀和外汇波动的影响)；资本投入为实际资本存量(rkna，以 2011年不变全国价格衡量)；劳动投入为就业人数(emp)，由于部分国家在部分年份缺失数据，为此本文还根据美国经济咨商局(The Conference Board)提供的经济总量数据库(Total Economy Database，TED)来补充就业数据，从而获取了较为完整的数据面板。

由于测算生产效率要求产出和投入都不存在缺失值，因此在进行SFA分析时，本文选取了3个变量均不存在数据缺失的观测值进行分析。在时间范围的选择上，由于早期数据涵盖的国家范围较小①考虑到实际GDP、资本存量和就业人数都不存在缺失值的情况，1950年的样本数据仅包括50个国家，1960年为83个样本。，本文以 1970年至 2014年为时间段，选取了104个国家或地区进行分析，以保证数据能够包含尽可能多的样本；而根据 PWT 9.0(2016)的统计，这些国家或地区的实际GDP、实际资本存量和就业人数占世界总量的比重分别在90%以上②1970年，这104个国家的实际GDP、实际资本存量和就业人数占世界总量的比重分别为98.88%、99.31%、91.15%，而到2014年的占比分别为93.37%、95.11%、92.93%。，具有高度的代表性。SFA法测算的 TFP增长率和分解后的技术效率变化、技术变化情况如表2所示。

表2 TFP增长率、技术效率变化和技术变化的描述性统计

四、实证分析

根据假说 1～2，初等教育型人力资本结构占比的提高将会促进技术效率变化，而高等教育型人力资本结构占比的提高将会促进技术变化。为此，本文将设计实证模型来检验这些假说。根据第三部分的测算结果，人力资本结构只包括每隔五年的测算数据，即 1950年、1955年、……、2010年等的数据，而 TFP分解的数据则每年都有。为了与人力资本结构数据相匹配，同时剔除经济周期波动和随机因素对技术进步的干扰，本文分别对技术效率变化率和技术变化率求解了5年和10年的平均增长率。计算公式如下：

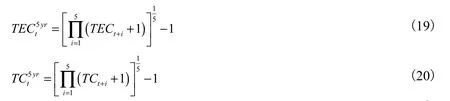
根据式(19)和式(20)，本文计算了技术效率变化和技术变化的 5年平均增长率③由于缺少2015年的实际资本存量和就业人数数据，我们无法测算和分解2015年的技术进步率，因此也无法计算2010年的5年平均增长率。为了丰富样本量，对于2010年我们通过计算4年平均增长率加以代替，即用2011年、2012年、2013年、2014年的数据来计算。。在此基础上，我们将技术进步数据同测算好的 136个国家或地区的人力资本结构数据进行匹配，最后共得到 95个国家或地区①这 95个国家或地区包括：阿尔巴尼亚、阿拉伯联合酋长国、阿根廷、澳大利亚、奥地利、比利时、孟加拉国、保加利亚、巴林、玻利维亚、巴西、巴巴多斯、加拿大、瑞士、智利、中国大陆、科特迪瓦、喀麦隆、哥伦比亚、哥斯达黎加、塞浦路斯、德国、丹麦、多米尼加、阿尔及利亚、厄瓜多尔、埃及、西班牙、芬兰、法国、英国、加纳、希腊、危地马拉、中国的香港特别行政区、洪都拉斯、海地、匈牙利、印度尼西亚、印度、爱尔兰、伊朗、伊拉克、冰岛、以色列、意大利、牙买加、约旦、日本、肯尼亚、柬埔寨、韩国、科威特、斯里兰卡、卢森堡、摩洛哥、墨西哥、马里、马耳他、缅甸、莫桑比克、马拉维、马来西亚、尼日尔、荷兰、挪威、新西兰、巴基斯坦、巴拿马、秘鲁、菲律宾、波兰、葡萄牙、巴拉圭、卡塔尔、罗马尼亚、沙特阿拉伯、苏丹、塞内加尔、新加坡、瑞典、叙利亚、泰国、特立尼达和多巴哥、突尼斯、土耳其、坦桑尼亚、乌干达、乌拉圭、美国、委内瑞拉、越南、南非、赞比亚、津巴布韦。9个时期(1970年、1975年、……、2010年)的平衡面板数据。值得注意的是，选取这95个国家或地区进行回归分析同样具有较高的代表性和可靠性。1970—2010年，这些国家的实际 GDP、实际资本存量和就业人数占世界总量的比重均在85%以上。

我们首先观察人力资本结构与技术效率变化以及技术变化之间的关系，如图2所示：

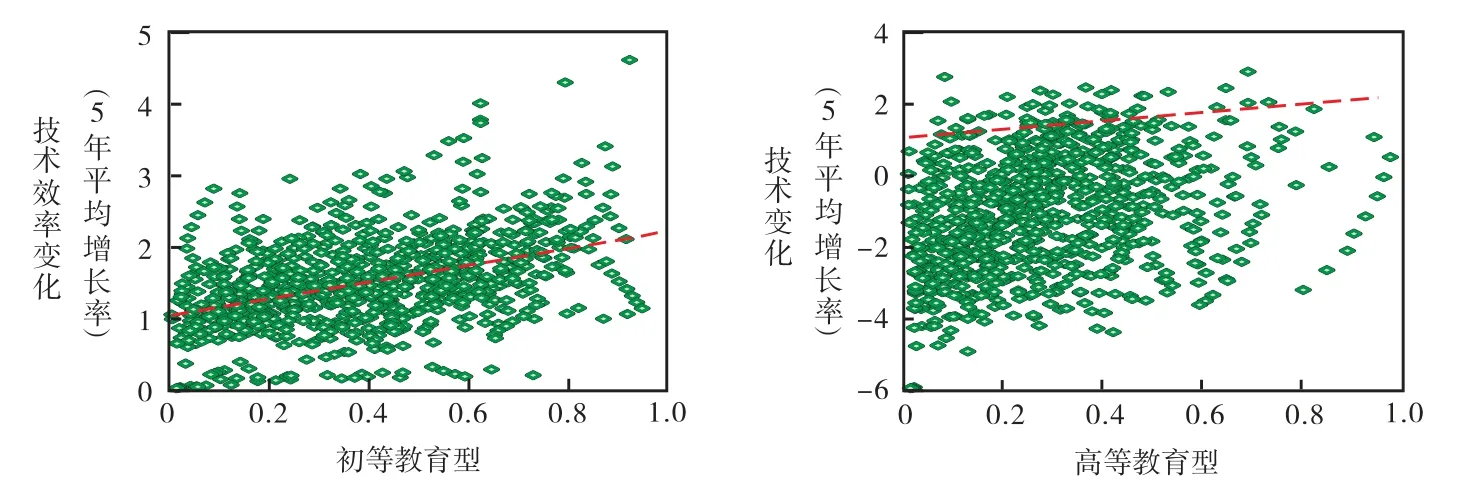
图2 人力资本结构与技术效率变化和技术变化之间的相关关系

图2表明，初等教育型的人力资本结构占比与技术效率变化之间、高等教育型的人力资本结构占比与技术变化之间均存在着正相关关系，这与我们的理论假说相一致。为了获得更加稳健的经验证据，本文将进行系统的实证分析。

（一）计量模型与变量选取

在计量模型设定方面，本文主要借鉴了 Benhabib和 Spiegel(1994、2005)、Dowrik和 Rogers(2002)等提出的技术扩散模型，该模型的特别之处在于引入了经济体接近技术前沿的程度，以控制技术追赶的影响；Vandenbussche等(2006)、Ang等(2011)、Cerina和Manca(2016)等也都利用该模型探讨了不同类型的人力资本结构随技术前沿距离的变化所产生的差异性影响。同时，考虑到技术效率变化与技术变化之间可能存在相互影响的关系，本文在分别考察人力资本结构对技术效率变化和技术变化的影响时，相对应地将技术变化和技术效率变化作为解释变量引入到模型当中。具体的实证模型如下所示：

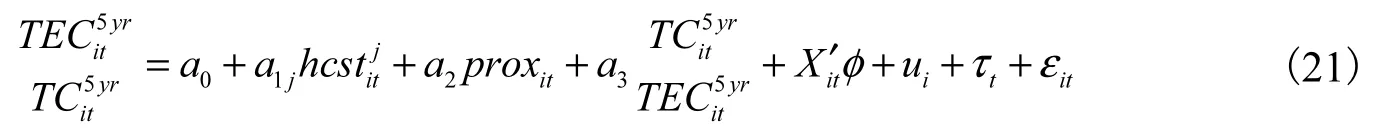
1.经济发展水平(lnpgdp)，用初始人均 GDP的自然对数来表示，包括 1950年、1955年直到 2010年的数据。由于在不同的经济发展阶段人力资本结构对技术进步的影响可能存在差异，因此引入该变量加以控制。为了消除通货膨胀和外汇波动的影响，GDP采用链式购买力平价和2011年不变美元价格来衡量。

2.人力资本存量(lnh)，具体测算方法见第三部分。引入该变量的原因在于控制人力资本对技术进步的存量影响，从而更加准确地考察人力资本对技术进步的结构性影响。

3.投资率(csh_i)，用资本形成总额占 GDP的比重来表示。根据“干中学”等内生增长理论，企业增加物质资本投资的同时也会提高生产效率，因此资本存量的增加也会对技术进步产生影响，尤其会提高技术的应用水平。

4.政府消费率(csh_g)，用政府消费占 GDP的比重来表示，由于政府消费可能会扭曲私人决策，因此该变量反映了政府活动本身或者公共财政所产生的不利影响。

5.劳动人口占比(labor)，用劳动就业人数占总人口的比重来表示，引入该变量的原因在于，劳动规模的扩大会增加研发新技术的概率。

6.对外开放度(open)，用对外进出口总额占GDP的比重表示，由于对外开放度的提高有利于技术信息的交流和扩散，因此引入该变量有助于控制技术扩散对技术进步的影响。

7.外商直接投资引入程度(fdi_in)，用外商直接投资净引入额占 GDP的比重来表示，以反映潜在的技术引进对技术进步的影响。

8.工业化进程(industry)，用工业增加值占 GDP的比重来表示，以反映各国的工业化水平。引入该变量的原因在于，随着工业化水平的提高，技术应用和技术创新的能力也会发生相应改变。

9.城镇化水平(urban)，用城镇人口占总人口的比重来表示，以反映城乡二元结构的变动对技术进步的影响。

10.通货膨胀率(cpi_gr5)，用各5年期(1950—1955年，等等)的消费者价格平均增长率来表示，以度量宏观经济的稳定性。

11.生育率(lnfer)，用女性人均生育数的自然对数来表示，由于生育率对人口增长而言非常重要，因此该变量反映了人口变化对技术变化的影响。

12.总抚养比(dr)，用被抚养人口(15岁以下及 64岁以上人口)与劳动年龄人口(15～64岁人口)之比，体现了每百名劳动年龄人口中被抚养人口所占的比例。由于不同年龄段的人口在技术应用和技术创新方面发挥的作用存在差异，控制该变量可以控制人口结构对技术进步的影响。

13.民主程度(pr)，用选举权来衡量，该数据来自于非政府组织“自然之家”(Freedom House)提供的世界各国民主排名，从 1到 7表示民主程度的恶化。根据Acemoglu和 Robinson(2012)的分析，汲取性制度(extractive institution)不会导致创造性破坏，无法产生持续的技术变革，因此在汲取性和包容性(inclusive)的政治制度下，技术创新激励并不相同，这会对技术进步产生差异性影响。因此，我们引入该指标来试图反映制度差异的影响。此外，考虑到民主程度对经济增长的非线性影响(Barro和Sala-i-Martin，2003)，我们同时引入二次项进行分析。

值得注意的是，技术前沿距离、对外开放度以及外商直接投资引入程度均从不同方面刻画了经济全球化带来的技术扩散对本国技术进步的影响。控制这些变量将有助于我们准确地观察人力资本结构对技术进步的净影响。

除人力资本之外，其他变量的数据主要来自于世界银行的WDI数据库。各控制变量的描述性统计及其数据来源如表3所示。

本模型主要采用面板数据回归方法进行实证分析。为了提高分析结果的稳健性，本文将在基础回归的基础上充分考虑面板数据可能存在的自相关问题和异方差问题，通过稳健性检验来对回归结果进行修正。考虑到国家之间差异较大，使用固定效应模型可以便于我们有效控制不可观测因素的影响。

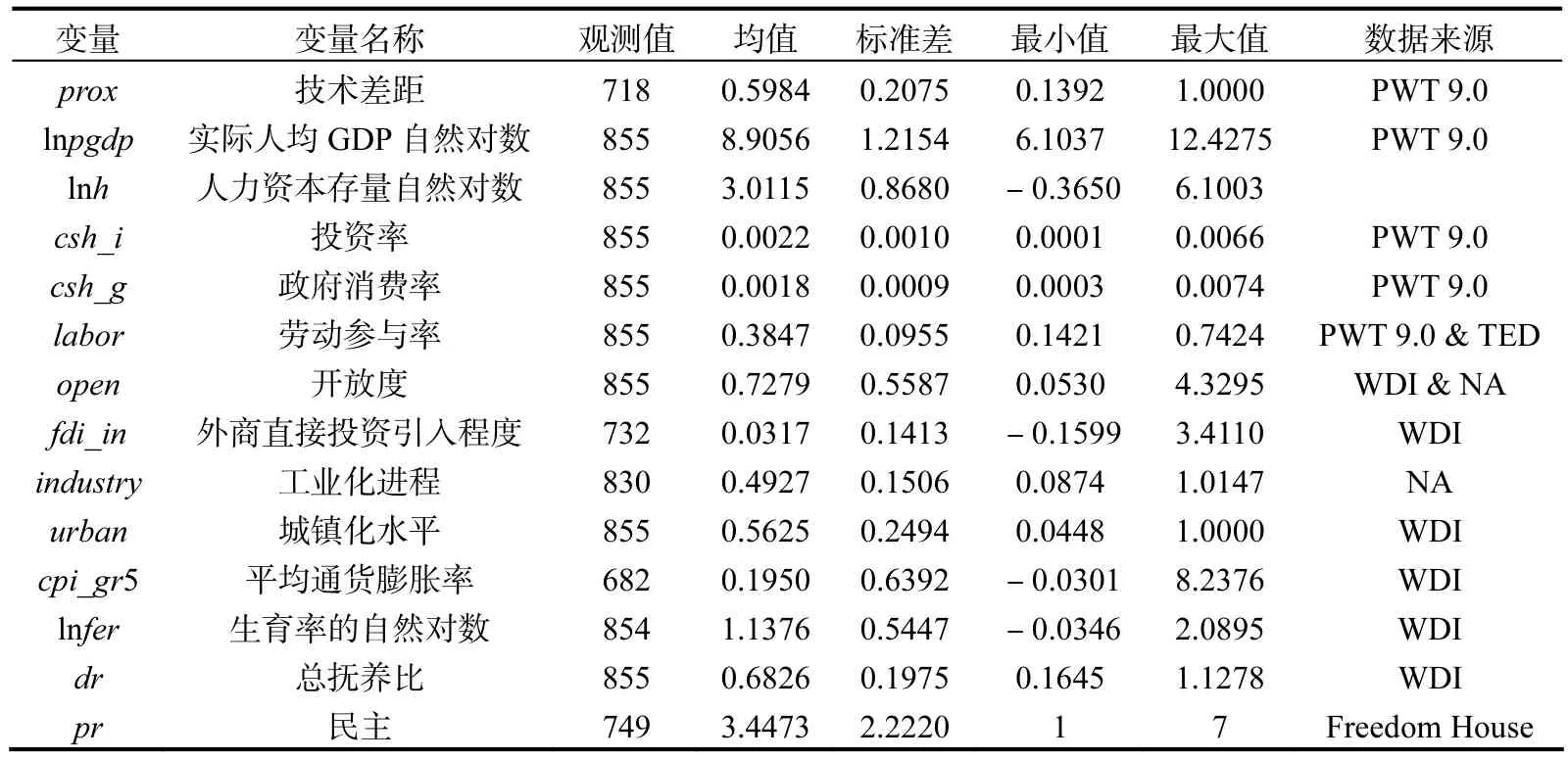
表3 各控制变量的描述性统计和数据来源

（二）基本实证结果

Hausman检验的结果显示，本文的计量模型更适合使用固定效应模型进行分析。固定效应回归结果如表4所示。

表4 固定效应回归结果

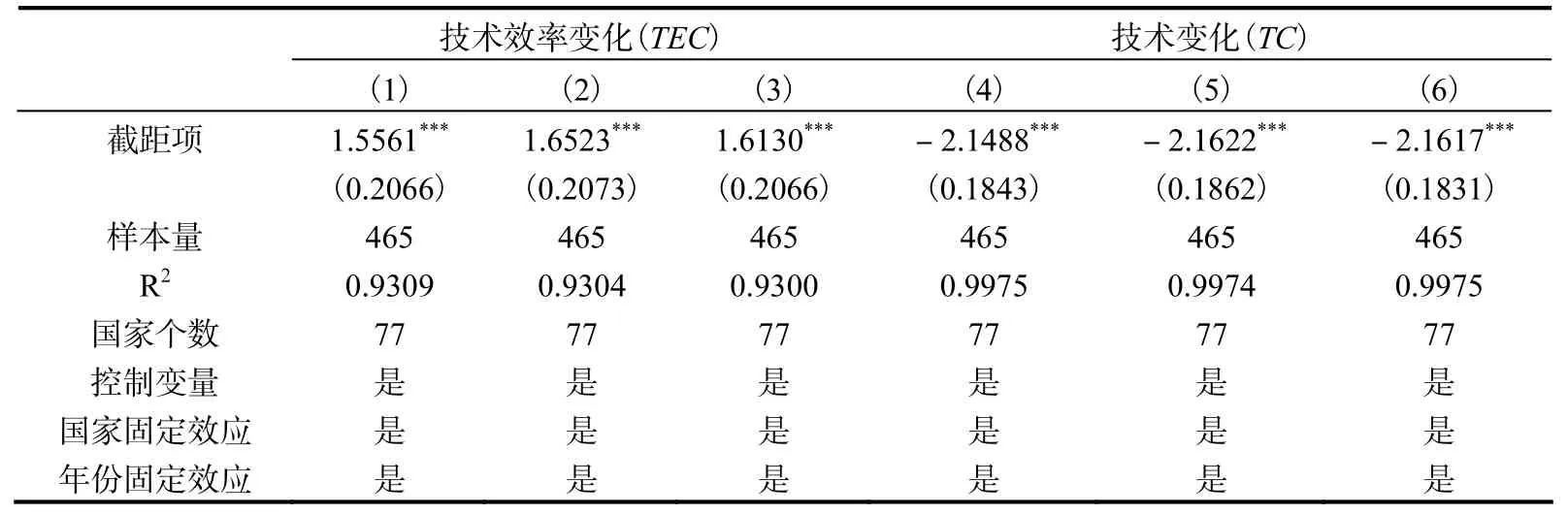
续表4

固定效应的回归结果表明，在技术效率变化模型中，初等教育型人力资本结构占比(hcpst)的系数显著为正，而在技术变化模型中，高等教育型人力资本结构占比(hchst)的系数为正并且在15%的置信水平上显著。这表明提高初等教育型人力资本的结构占比能够显著促进技术效率变化，而提高高等教育型人力资本的结构占比能够显著促进技术变化，这与我们的理论分析相一致。换言之，初等教育型人力资本结构占比的提高有利于促进技术应用，而高等教育型人力资本结构占比的提高则有利于促进技术创新。然而，中等教育型资本结构占比(hcsst)的系数为负并且均不显著，这意味着，对于技术效率变化和技术变化而言，中等教育型人力资本结构占比的变化并不能产生显著影响。此外，技术效率变化(TEC)和技术变化(TC)之间存在显著的正相关关系，这表明两者之间存在着相互促进的作用。值得注意的是，在模型(6)中，高等教育型人力资本结构占比的系数显著程度并不是很高，其原因可能在于跨国数据的样本异质性较高，不免存在异方差等问题，因此还需要通过稳健性回归加以修正。

（三）稳健性分析

XTSCC模型是在固定效应模型的基础上综合考虑面板数据存在的异方差和自相关性等问题，对系数标准误进行修正(Driscoll和Kraay，1998)。使用XTSCC模型的回归结果如表5所示。

XTSCC模型的回归结果表明，即使解决了异方差和自相关性等问题，初等教育型人力资本的结构占比(hcpst)仍然能够对技术效率变化产生显著为正的影响，高等教育型人力资本的结构占比(hchst)仍然对技术变化产生显著为正的影响。这与基本结论保持一致，从而表明假说1和假说2所体现的人力资本结构与技术进步之间的关系并不受异方差和自相关性等问题的干扰。中等教育型人力资本结构占比的系数在技术效率变化模型中显著为负，而在技术变化模型中符号并不确定，可见中等教育型人力资本结构占比的提高并不利于技术应用，但对技术创新的影响并不明确。

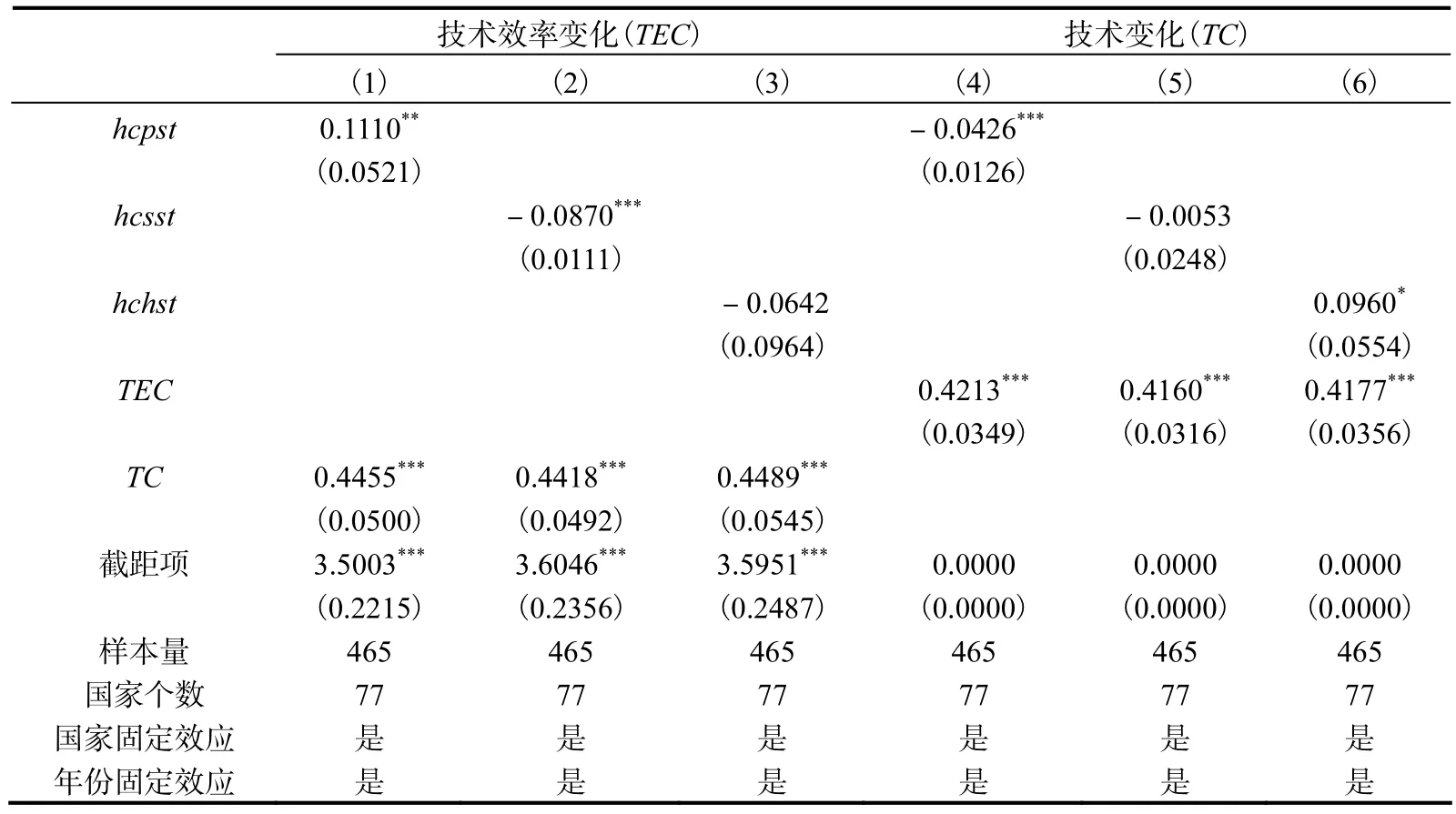
表5 稳健性分析结果(XTSCC模型)

值得注意的是，本文匹配成功的人力资本结构和技术进步数据包括 95个国家或地区、共 855个样本量。然而，由于引入的控制变量存在不同年份的数据缺失，而在回归分析的时候会自动删除存在数据缺失的样本，导致最后的样本量会大为减少(表4中样本量为 465个)。因此，为了增强分析结果的可靠性，本文还考虑了减少控制变量的问题，即只引入人力资本总量(lnh)以更加准确地考察人力资本结构的影响，同时采用 XTSCC模型来解决异方差和自相关问题。其结果表明，在减少控制变量后，回归样本量达到855个，样本个数也包括了匹配成功的所有国家或地区。同样，对于技术效率变化而言，初等教育型人力资本的结构占比(hcpst)仍然显著为正；对于技术变化而言，高等教育型人力资本的结构占比(hchst)仍然产生显著为正的影响。这与基本结论保持一致，从而表明了实证分析结果比较可靠，在一定程度上不受样本选择问题的影响。囿于篇幅限制，本文不再汇报减少控制变量的XTSCC模型回归结果，有需要者可以向作者索取。

（四）联立方程模型

由于在技术效率变化模型和技术变化模型中，我们分别对应地引入了技术变化和技术效率变化，这意味着技术效率变化模型中解释变量是技术变化模型中的被解释变量，这将有可能产生内生性问题。为了解决内生性偏差或联立方程偏差，除了单方程估计外，我们还考虑了联立方程估计。为了保证联立方程模型能够识别，即满足“秩条件”和“阶条件”，同时能够着重检验假说1和假说2，我们构造了两组恰好识别的联立方程模型来予以验证，具体如下所示：

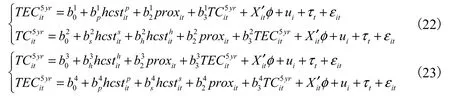
在第一组联立方程(22)中，技术效率变化模型的核心解释变量为初等教育型人力资本结构占比技术变化模型中的核心解释变量为中等教育型和高等教育型人力资本结构占比在第二组联立方程(23)中，技术变化模型的核心解释变量为高等教育型人力资本结构占比技术效率变化模型中的核心解释变量为初等教育型和中等教育型人力资本结构占比我们利用三阶段最小二乘法(3SLS)对式(22)和式(23)加以分析，具体结果如表6所示。

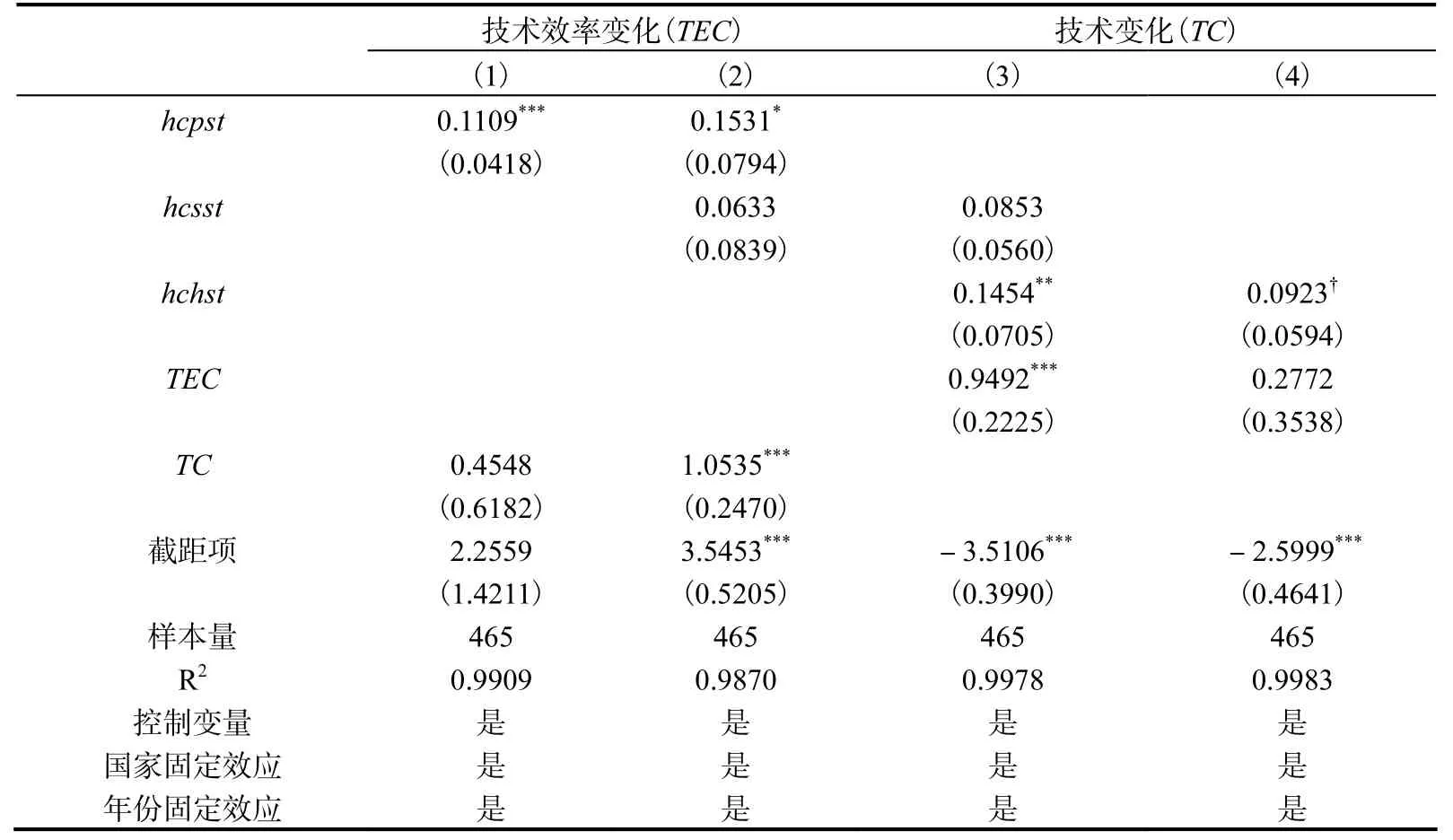
表6 联立方程模型估计结果

联立方程模型的估计结果表明，即使考虑了内生性偏差和联立方程偏差问题，在技术效率变化模型中，初等教育型人力资本结构占比的系数仍然显著为正；同样，在技术变化模型中，高等教育型人力资本结构占比的系数仍然显著为正，这与基本结论保持一致。对于中等教育型的人力资本结构占比而言，系数符号并不明确且不显著。除了上述联立方程组之外，我们在满足联立方程识别条件的基础上，还考虑了其他形式的联立方程模型，包括①TEC(h cs )表示在技术效率变化模型中核心解释变量为初等教育型人力资本结构占比； TC(h cs)表示在技术变化模型中核心解释变量为中等教育型人力资本结构占比。、等，基本结果仍然保持不变。可见，假说1和假说2的基本结论具有稳健的实证基础。

五、进一步的讨论

当经济体逐步接近技术前沿时，不同类型的人力资本对技术进步的影响程度也会发生改变。为了进一步考察在技术水平或者经济发展水平不同的国家里人力资本结构对技术进步的影响是否具有异质性，本文还尝试进行了分样本回归，即根据联合国统计署(UNSD)的划分标准将样本总体分为发展中地区和发达地区两部分②发达地区和发展中地区的分类标准来自于联合国统计署的 Standard Country or Area Codes for Statistical Use(M49)，详见：https：//unstats.un.org/unsd/methodology/m49/。，分别以计量模型式(21)为基础进行XTSCC模型回归分析。

分样本的回归结果表明，在发展中地区和发达地区，不同类型的人力资本结构占比对技术效率变化和技术变化的影响存在异质性③囿于篇幅限制，本文不再汇报分样本的回归结果，有需要者可以向作者索取。。那么，这种异质性影响是否存在系统性规律？其背后的影响机制是什么？为了系统地探讨人力资本结构对技术进步的影响因技术水平或经济发展水平不同而表现出的异质性规律，我们还借鉴相关研究的普遍做法，从跨国技术水平差距入手，将技术前沿距离和人力资本结构之间的交互影响引入到基本回归方程式(21)中，以观察不同类型的人力资本结构随技术前沿距离的变化(即在技术水平或经济发展水平不同的经济体中)对技术效率变化和技术变化所产生的差异性影响。则式(21)可变为：

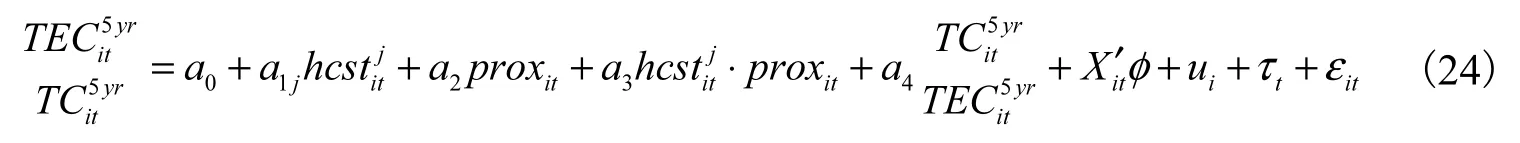
引入人力资本结构与技术前沿距离交互项的XTSCC模型表明，人力资本结构对技术进步的影响会随着技术前沿距离的变化而发生改变。首先，在技术效率变化模型中，初等教育型人力资本结构占比的一次项(hcpst)系数显著为正，而交互项(hcpst×prox)系数显著为负；中等教育型和高等教育型人力资本结构占比的一次项(hcsst和hchst)系数显著为负，而交互项(hcsst×prox和 hchst×prox)系数显著为正。这表明，随着经济体接近技术前沿，初等教育型人力资本结构占比的提高会促进技术应用，而促进程度会逐步减弱；中等教育型和高等教育型人力资本结构占比的提高会抑制技术应用，而抑制程度会逐步减弱。其次，在技术变化模型中，初等教育型人力资本结构占比的一次项(hcpst)系数显著为负，而交互项(hcpst×prox)系数显著为正；中等教育型人力资本结构占比的一次项(hcsst)系数显著为正，而交互项(hcsst×prox)系数显著为负；高等教育型人力资本结构占比的一次项(hcsst)系数为正并且在 15%的置信水平上显著，交互项(hcsst×prox)系数为负但不显著。不显著的原因可能在于，经济发展水平较高的经济体往往更接近技术前沿，技术进步活动更多依赖于技术创新而非技术应用，所产生的技术变化更为明显。当我们不再控制经济发展水平时，XTSCC模型的回

归结果表明高等教育型人力资本结构占比的一次项和交互项系数均高度显著(置信水平为 1%)。可见，对于技术创新活动而言，随着经济体接近技术前沿，初等教育型人力资本结构占比的提高所带来的抑制作用会逐步减弱；同样，提高中等教育型和高等教育型人力资本结构占比所带来促进作用也会逐步减弱。综合技术效率变化和技术变化两个模型的回归结果，我们发现不同国家或地区之间的技术水平差距是导致异质性影响产生的关键因素。因此，对于给定经济而言，在趋近技术前沿的过程中注重发挥不同类型人力资本的异质性作用就显得尤为重要。

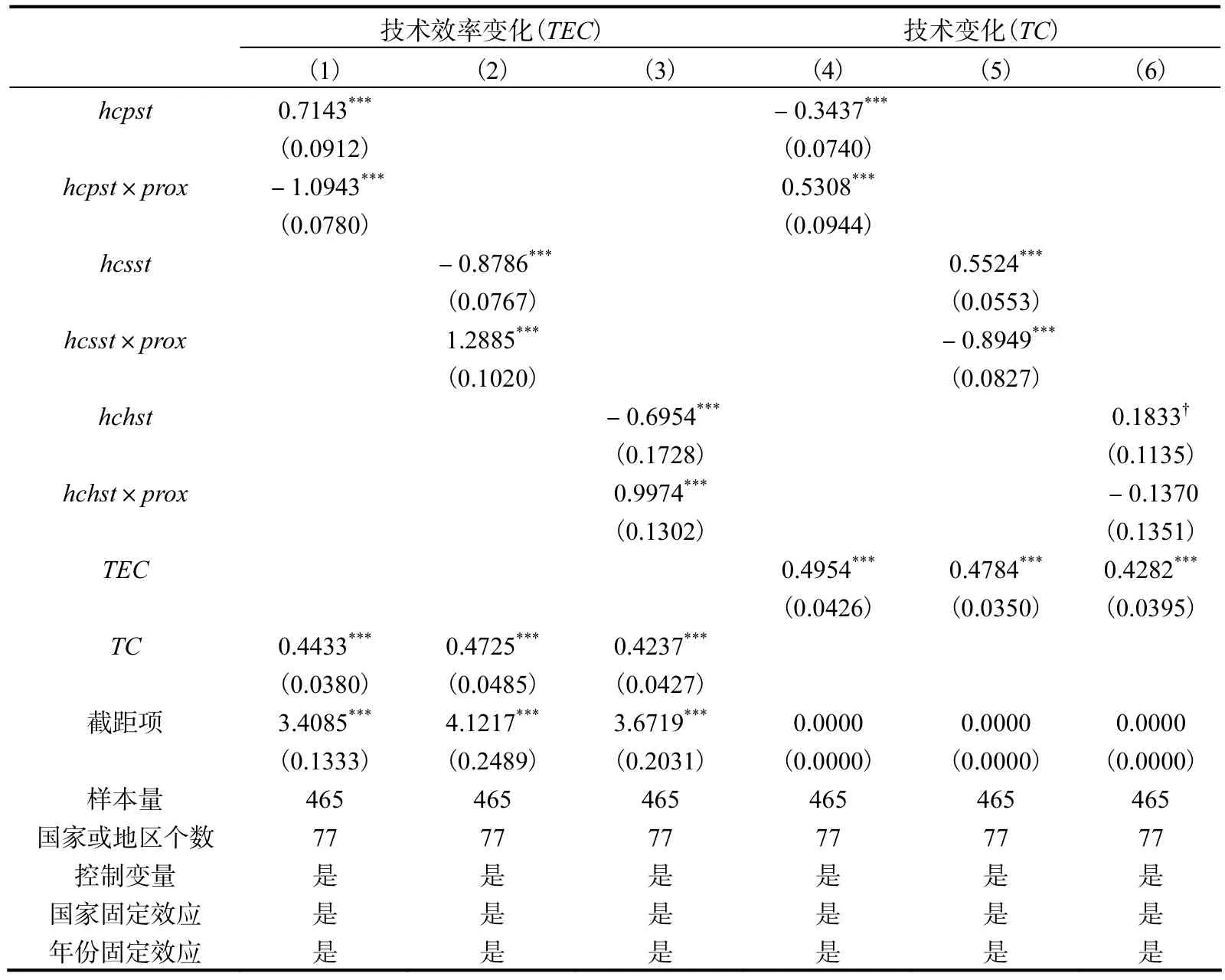
表7 人力资本结构和技术前沿距离的交互影响(XTSCC模型)

六、主要结论和启示

本文以跨国面板数据为基础，通过测算各国或地区的人力资本结构和技术进步产生的效率变化，进而深入分析了人力资本内部的结构性变化对技术进步的差异性影响，主要结论如下。

在理论方面，本文结合以往的研究文献，深入分析了不同类型的人力资本在技术应用活动和技术创新活动中的异质性作用，并据此提出研究假说，即初等教育型人力资本结构占比的提高将会提高技术应用水平，进而促进技术效率变化；而高等教育型人力资本结构占比的提高能够有效促进技术创新活动，进而促进技术变化；中等教育型人力资本结构占比的变化对技术创新和技术应用都能产生影响，但是相对影响性质并不确定。

在实证方面，本文首先提出了测算初等教育型、中等教育型和高等教育型人力资本及其相对结构的方法，然后又利用随机前沿分析法和 Malmquist指数分解法对各国或地区技术进步产生的效率变化进行了测算和分解。据此，本文利用跨国面板数据实证分析了各类型人力资本结构对技术效率变化和技术变化的影响，基本实证结论支持了理论研究假说。在利用 XTSCC模型解决了异方差性和自相关性等问题以及利用联立方程模型解决了内生性问题之后，分析结果与基本实证结论保持高度一致。值得注意的是，本文的进一步讨论表明，在经济体趋近技术前沿的过程中，各类型人力资本结构占比的变化对技术效率变化和技术变化的影响程度会逐步减弱，人力资本结构对技术进步呈现出边际影响递减的趋势。

综上所述，本文发现人力资本结构能够对技术效率变化和技术变化产生异质性影响。对于经济发展水平不同的国家尤其是发展中国家而言，该结论具有以下重要的政策启示：第一，采取合适的人力资本投资战略对于经济发展而言至关重要。对于发展中国家而言，应当根据本国的经济发展状况来制定相应的人力资本投资战略，避免因追求跨越式的发展战略而过度投资于高等教育型人力资本，这会造成人力资本的内部结构失衡，最终会对经济增长产生不利的影响。第二，就我国而言，注重人力资本内部的结构性改革意义更为重要。目前，随着我国经济进入新常态，为了应对经济增长所面临的结构性问题，国家提出了“供给侧结构性改革”发展战略，强调经济的结构性改革。人力资本作为经济增长的重要供给要素之一，其内部的结构性改革正切题中之义。随着我国进入中等收入国家行列，技术创新在经济持续增长中的重要性日益突显，为此国家提出创新驱动战略以培育经济增长新动能，而创新的关键则在于高等教育型人力资本的培养。以 2010年为例，我国的高等教育型人力资本结构占比仅为 7.36%，低于世界平均水平(11.79%)。根据第三部分的分析，影响高等教育型人力资本积累的因素包括教育收益率、受教育年限和受教育人口占比三个方面。考虑到高等教育收益率具有较高的稳定性而不易改变，因此还有两种途径来促进高等教育型人力资本积累：一是普及高等教育，提高总人口尤其是工龄人口接受高等教育的比例；二是提高高等教育的完成率，尽可能增加高等教育的接受年限。所以，我国应当逐步优化人力资本的投资结构，以适应经济发展阶段和技术进步动能的转变，从要素供给和增长机制两个方面加力以促进经济的长期增长。