惊弓之鸟:流动性恐慌与股票价格
周爱民 葛 琛 遥 远
一、引 言
流动性是金融资产的重要特征,也是风险的重要来源。研究表明,流动性对资产价格存在显著影响,不可分散的流动性风险是系统性风险的重要组成部分。值得注意的是,次贷危机以来的众多研究表明,传统的流动性资产定价模型存在缺陷。一方面,危机时期的资产流动性打破了均值回复性,呈现出自我强化加速下滑的特征。另一方面,投资者存在“惊弓之鸟”的特征,对可能出现的危机的恐惧,即使在正常时期也会产生风险溢价。这些特征既会对投资实务造成重大影响,也表明传统的流动性资产定价理论仍有进一步扩展的空间。特别是2015年和2016年中国股票市场发生的市场流动性枯竭与股市暴跌,更突出了这一问题的重要性。
关于流动性风险与资产价格的关系问题,已有充分的理论和实证研究。Acharya和Pedersen(2005)建立的LCAPM(liquidity adjusted CAPM)是其中的代表,其将流动性成本引入投资者效用函数,从效用最大化出发,建立了包含四个 beta值的结构化定价模型。此后,Liu(2006)简化了 LCAPM,建立了包含市场风险和流动性风险的两因子模型,发现其比Fama-French三因子模型有更好的拟合效果和解释异象的能力。此外,黄峰和杨朝军(2007)以及周芳和张维(2011)等学者均认为,中国股票市场有明显的流动性驱动特征,流动性资产定价模型显著优于其他传统模型。
但若与次贷危机以来关于流动性危机和尾端风险的文献相结合,则可发现传统的流动性资产定价理论仍有缺陷。
一方面,极端状况下的流动性水平和流动性风险,表现出与正常时期完全不同的特征,而具有均值回复性的传统流动性因子不足以描述危机时的特征,可能在危机时期失效。流动性风险超过一定阈值后不再均值回复而是加速下滑,存在自我强化的机制,形成“流动性黑洞”或“流动性螺旋(liquidity spiral)”,最终造成流动性危机。流动性负向的自我强化可能由以下机制造成。第一,Morris和 Shin(2004)以及郭乃幸和杨朝军(2011)的“流动性黑洞”模型表明,当资产价格下降到短期投资者的止损线时,就会发生大规模的流动性踩踏。投资者的止损抛售造成资产价格进一步下跌,从而触发更多投资者的止损操作,出现资产价格和流动性相互影响的负向螺旋,最终造成流动性危机。第二,Brunnermeier和 Pedersen(2008)发现,存在融资交易时,融资流动性(funding liquidity)和市场流动性会形成相互强化的负向螺旋。在融资融券交易实行后,这一机制在中国市场上表现得更为明显。在该模型中,市场流动性下滑,资产价格下跌时,投资者的融资能力受限,迫使其卖出资产,使市场流动性进一步下滑。第三,Garleanu和 Pedersen(2007)发现,市场低迷风险激增时,所有机构同时采取严格的风控措施,会进一步加剧流动性紧张。以上三个理论均表明,均值回复特征明显的传统的流动性风险因子在危机时期会失灵。
另一方面,投资者对可能出现的危机的恐惧,是系统性风险的来源,即使在正常时期,也存在对极端风险的溢价,存在“惊弓之鸟”的特征,而传统的定价模型遗漏了这部分系统性风险。该思想源于 Barro(2006)、Bollerslev和 Todorov(2011)以及 Gabaix(2012)对罕见灾害(rare disaster)和股权溢价之谜的研究,投资者对难以预期的极端事件的恐惧造成了过高的风险溢价。基于该思想,Bali等(2009,2014)以及Huang等(2012)发现,由 VaR、Shortfall和极值理论等方法构造的尾端风险指标,均对收益率有显著的影响,这对传统的资产定价模型而言是一种难以解释的异象。Kelly和 Jiang (2014)是这一问题的集大成者,其基于幂律分布(power law distribution)假设和Hill估计量构造了收益率的尾端风险因子,发现该因子对个股和市场收益率均存在显著的解释能力,是不可分散的系统性风险。Kelly和Jiang(2014)以及Van Oordt和Zhou (2016)均认为系统性的尾端风险在市场下跌期间对资产价格具有重要的解释能力,相比传统因子而言显著增大,加入这些因子可以解决传统定价模型在危机期间失效的问题。
综上所述,传统的流动性资产定价模型存在两个重要缺陷,即难以描述极端情况下的流动性风险变化规律且遗漏了部分风险溢价,故有必要进行修正,以应对类似2015年和 2016年中国股票市场流动性枯竭的极端情况。正如赵胜民等(2016)指出,因子模型的有效程度因市场特征和投资理念而异,中国股票市场有明显的流动性驱动特征,流动性波动性较大。这表明考虑极端情况的流动性资产定价模型有更好的适用性。
本文将Kelly和Jiang(2014)以及Wu(2017)的框架进一步推广到中国股票市场的流动性问题中,基于幂律分布假设和 Hill估计量构造了极端流动性风险因子。相较于传统的流动性因子,本文所构造的极端流动性风险因子克服了上文所述的两个缺陷。在实证检验中本文发现了以下结论。第一,极端流动性风险因子在市场流动性恐慌时期显著增强,能提前指示2007年到2008年和2015年到2016年的两次危机,而传统的流动性因子在危机时期并未明显增强。第二,基于投资组合法和Fama-MacBeth回归法,本文发现极端流动性风险因子在横截面上存在显著的风险溢价,年化等权重组合约有9%的超额收益率,且可以消除反转效应等传统定价模型难以解释的市场异象。第三,将极端流动性风险因子与市场因子相结合构建的两因子模型,对横截面收益率的解释力高于其他经典模型,兼顾了解释力与简洁性。第四,极端流动性风险因子对未来市场收益率有显著的解释力,与 Welch和 Goyal(2008)以及姜富伟等(2011)的市场收益率可预测性框架相结合,极端流动性风险因子对预测的贡献度约为 15%。第五,由于极端流动性风险因子反映了投资者的预期,且股票市场的剧烈波动可能对宏观经济造成影响,基于脉冲响应图可发现极端流动性风险因子的冲击将伴随着未来一个月产出和投资的下滑,并有未来四个月的通货紧缩和资金面紧张。以上结论表明,本文构造的极端流动性风险因子在理论上完善了流动性资产定价模型,深化了对危机时期流动性特殊性质的认识,也对投资实务有一定应用价值。
二、极端流动性风险因子的构造
(一)极端流动性风险因子的基本假设
本文构造极端流动性风险因子的思路,源于 Kelly和 Jiang(2014)以及 Wu(2017)。Kelly和 Jiang(2014)最早用该思路构造了极端收益率风险因子。由于极端事件极少发生,样本积累稀少,故估计时变的尾端风险是困难的。为解决这一问题,Kelly和Jiang(2014)假设收益率的尾端服从幂律分布,该分布的关键参数可分为两部分,一部分由个股因素决定,另一部分由市场因素决定,此时便可从日常收益率中获得大量样本。据此,可使用 Hill(1975)的估计方法,从个股的尾端分布中计算由市场因素决定的参数,定义为极端收益率风险因子。这一方法简单便捷,得到了广泛应用。
与此同时,众多学者指出幂律分布是金融变量的普遍特征,不仅收益率的尾端服从幂律分布,流动性成本和价格冲击的尾端同样服从幂律分布。Plerou等(2004)发现,交易的价格冲击的尾端服从幂律分布,故传统的正态分布假设无法很好地描述流动性成本的尾端特征。Gabaix等(2003,2006)进一步指出,投资者的最优化交易行为,特别是大机构的行为,是形成幂律分布特征的原因。陈收等(2008)以及曹宏铎等(2011)发现中国市场的众多变量也广泛存在幂律分布特征。据此,我们可以直接将 Kelly和Jiang(2014)的理论扩展到流动性问题中。
综上所述,可以假设流动性成本的尾端分布如下:
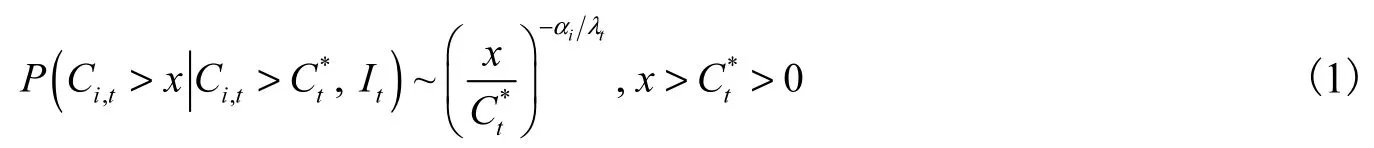
其中Ci,t表示股票i在t时刻的流动性成本,为某一阈值,要求为信息集,参数决定了尾端分布的形状。由于故应有保证概率取值在0到1之间。参数由两部分构成,其中iα由个股因素决定,tλ由市场因素决定并随It变化。
(二)极端流动性风险因子的估计方法
定义tλ为市场在t时刻的极端流动性风险,则可使用Hill(1975)提出的分布尾端估计方法来估计tλ,即:

其中Ck,t是超过阈值的日度流动性成本。将每个月内所有股票的日度流动性成本带入式(2),即可得到该月的极端流动性风险因子值,Kt为月内符合条件的日观测值的数量。在每个月内,个股出现极端低的日流动性水平的频率越高,则加总而成的统计量就越显著,全市场的极端流动性风险就越大。个股的流动性水平是投资者预期和交易行为的结果,故式(2)在本质上也反映了全市场范围内投资者的预期和交易行为,这是其解释能力和预测能力的来源。
由于幂律分布的对数服从同参数的指数分布,根据指数分布的性质可知:

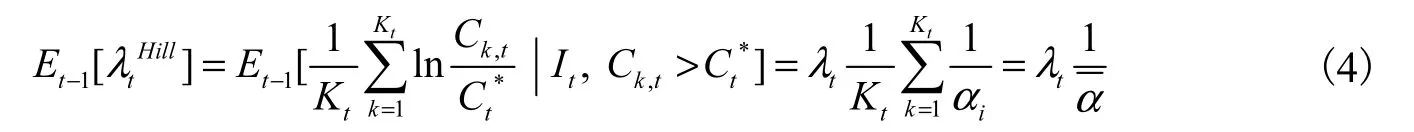
三、样本与指标定义
(一)样本区间的选择
本文选取的样本区间为2005年1月到2016年12月。由于股权分置改革对流动性影响较大,且 2005年之前样本量较少,不利于极端流动性风险因子的估计,故样本时间从 2005年开始。该区间包含了中国股票市场最为标志性的两次暴跌,具有代表性。此外,我们删除了金融股和当年上市的股票样本,但在稳健性检验中加入这些样本后并不影响结论。
(二)极端流动性风险因子及其beta值的计算
基于式(2)可由个股的日度流动性成本计算出市场的月度极端流动性风险因子值。张峥等(2013)比较了各种度量方法在中国股票市场上的适用性,认为 Amihud指标适用性最好。该指标的计算方法如式(5)。

其中 daysi为个股月内有效交易天数。
图1即为按以上方法计算所得的极端流动性风险因子,阴影区域表示数次股灾,左轴为极端流动性因子值和 LCAPM 的传统流动性因子值,右轴为市场收益率。一方面,极端流动性风险因子在正常时期的波动率与传统流动性因子相当,但在危机前以及危机时期出现剧烈震荡,幅度远超传统的流动性因子。特别是 2015年到 2016年的股灾表现出明显的流动性枯竭特征,极端流动性风险因子的震荡更加明显,这说明极端流动性风险因子能更准确地描述流动性恐慌期的市场特征。另一方面,极端流动性风险因子对于两次大规模的股灾具有一定的提前指示作用,提前期约一个月。特别是2015年5月出现的剧变,预示大规模的流动性枯竭即将到来。
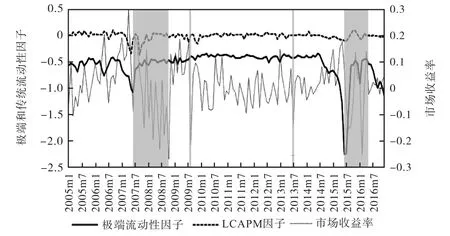
图1 极端流动性风险因子图
极端流动性风险因子对于危机的提前指示能力,可能源于其在微观层面捕捉了投资者的预期和交易行为。当市场狂热接近末期,投资者,特别是理性程度更高的机构投资者,对于显著高估的股票的预期和交易行为逐渐趋同,出现“逃往质量(flight to quality)”现象。这种同质化的抛售行为使月内流动性样本的尾端显著增厚,从而使极端流动性风险因子出现剧变。
为计算个股对极端流动性风险因子的beta值,我们用个股超额收益率与该因子的非预期变化(unexpected innovation)做了 24个月的滚动回归。在稳健性检验中我们也尝试了 60个月的滚动回归,结果并无区别。求因子非预期变化的常用方法主要有Pastor和 Stambaugh(2003)以及 Sadka(2006)。我们采用了 Sadka(2006)的 ARIMA模型残差法。具体而言,我们对极端流动性风险因子序列建立ARIMA模型①基于Box-Jenkins方法最终选择的最优模型为ARIMA(2,1,2)。,取残差作为极端流动性风险因子的非预期变化,与个股超额收益率做滚动回归。
(三)其他变量定义
在个股层面,我们选取的控制变量包括:流通市值(Size)、账面市值比(Bmratio)、动量效应(Momentum)、盈利性(Roe)、换手率(Turnover)、流动性水平(Liquidity)和波动率(Volatility)。在市场层面,我们参考了Welch和Goyal(2008)以及姜富伟等(2011)的市场收益率可预测性框架,选择的控制变量包括:平均市盈率(Peratio_m)、平均账面市值比(Bmratio_m)、市值变动率(Size_delta_m)、平均股利支付率(Dividend_m)、平均换手率(Turnover_m)、平均流动性水平(Liquidity_m)、通货膨胀率(Inflation_m)和货币供应量(M2_m)。
四、个股层面的实证分析
(一)极端流动性风险因子的横截面风险溢价
为验证本文所构造的极端流动性风险因子存在显著的风险溢价,我们首先使用单变量组合分析法。具体而言,我们在每个月将样本按极端流动性风险因子 beta值从大到小排序,等分为五个组合,分别计算各组合持有一定期限后的平均超额收益率,最后求各月各组合的均值。若按顺序排列的各组合的平均超额收益率存在一定程度上的递增关系,且最高组与最低组的平均超额收益率之差显著大于零,则可认为极端流动性风险因子存在显著的风险溢价。为确保结论的稳健性,我们采用了多种组合构造方法:持有期限包括1个月、3个月、6个月和12个月;超额收益率包括基于Fama-French三因子和五因子模型调整的 alpha;加权方法包括等权重加权、流通市值权重加权和总市值权重加权。计算结果见表1。
为更直观地展示表1的结果,我们还依据各组的平均超额收益率绘制了图2,横轴为五个组合,纵轴为加权平均超额收益率。
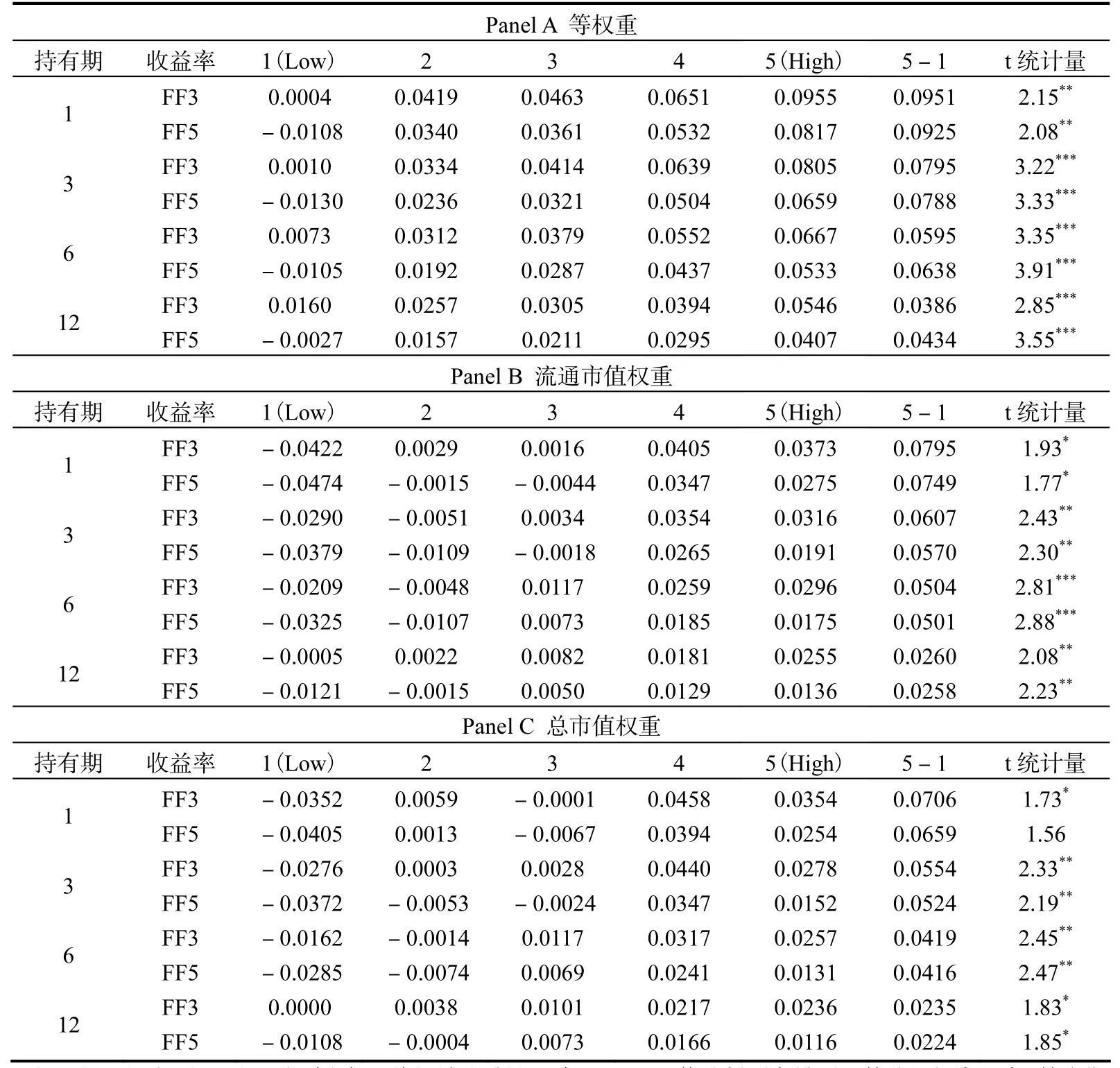
表1 极端流动性风险因子与个股收益率的投资组合分析
表1的计算结果显示,在24种不同组合构造方式下,最高组与最低组的平均超额收益率之差基本都显著大于零,表明该因子存在显著的风险溢价,且结果非常稳健。从图2可观察到,极端流动性风险因子beta值与超额收益率之间存在明显的正向关系①等权重的组合下可以保证单调性,但市值权重组合下,第4组的超额收益率往往是最高的。这可能是因为大市值的股票波动率相对较低,从而在加权后拉低了第5组的加权平均超额收益率。。
极端流动性风险因子存在横截面的风险溢价,对于传统资产定价模型而言是一种异象。这种溢价的来源,可能是由于投资者对于流动性枯竭出现的恐惧,即使在正常时期,也会因恐惧而影响交易行为,存在“惊弓之鸟”的特征。这与 Bali等(2009,2014)、Huang等(2012)、Kelly和 Jiang(2014)、陈国进等(2015)、Van Oordt和 Zhou(2016)、刘圣尧等(2016)以及 Wu(2017)的发现在逻辑上是一致的,只是这些研究更加关注收益率的尾端特征及其风险溢价,而本文则是从流动性的角度入手。该思想根源于对股权溢价之谜的研究。Barro(2006)、Bollerslev和 Todorov(2011)以及 Gabaix(2012)认为,由于罕见灾害难等极端事件难以被估计且危害性巨大,投资者对这类事件的恐惧造成了过高的风险溢价,即使在正常时期这种溢价依然存在,因此形成了股权溢价之谜。该结论也在一定程度上修正了传统流动性资产定价模型存在的缺陷,更好地描述了危机时期的特征,补充了这部分缺失的风险溢价。

图2 极端流动性风险因子与个股收益率的关系图
极端流动性风险因子对收益率的解释能力是否会被其他因素覆盖?为考察这一问题,我们进一步采用了 Fama-MacBeth回归方法,以便引入其他控制变量。除上文所述的常规控制变量外,我们还控制了Kelly和Jiang(2014)构造的极端收益率风险因子beta值。具体而言,极端收益率因子(KJ_factor)的计算方法与上文类似,只是将流动性成本改为收益率,在每月汇总所有样本的日收益率,基于同样的阈值确定尾端,并使用Hill估计量计算极端收益率风险因子,并求其beta值。
表2的回归结果表明,在加入众多控制变量后,极端流动性风险因子的风险溢价依旧在1个月、3个月和6个月的持有期限上显著,这种定价能力独立于极端收益率风险因子和其他因素,是一种全新的效应。
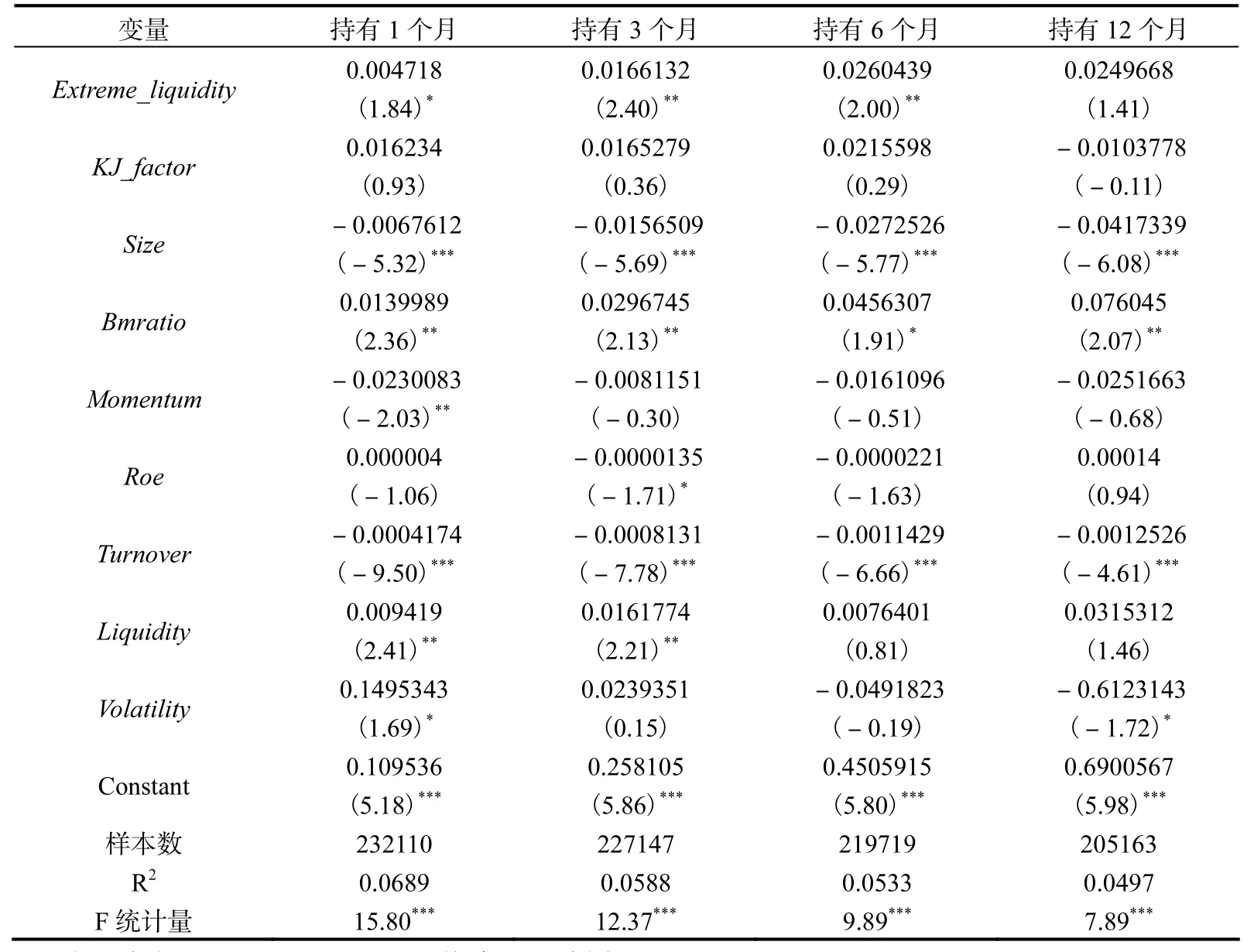
表2 极端流动性风险因子与个股收益率的Fama-MacBeth回归分析
(二)极端流动性风险与反转效应
能否解释各类市场异象,是评价资产定价模型优劣的重要方面。尽管 LCAPM 模型在解释规模效应和估值效应方面取得了良好的效果,但其能否解释中国市场上的反转效应仍存在争议。如陈青和李子白(2008)认为 LCAPM 模型可以在一定程度上解释反转效应,但李宏等(2016)基于更广泛的数据和更严谨的分析发现,LCAPM模型对于反转效应的解释很不充分。根据李宏等(2016)的定义,可用过去两个月的累计超额收益率代表短期反转效应(Reversal)。本文基于简单的方法发现,在控制极端流动性风险因子后,反转效应在各期限下均不再显著,这说明极端流动性风险因子可以解释短期反转效应,结果见表3。

表3 极端流动性风险因子与反转效应的回归分析
极端流动性风险因子对反转效应的解释能力,可能源于 Avramov等(2006)以及Nagel(2012)的理论。Avramov等(2006)认为,反转策略的收益在本质上可视为提供流动性获得的补偿。当投资者在下跌时买入资产,即提供了流动性,并可能获得反转的收益,以补偿其提供流动性的交易行为。Nagel(2012)发现,反转策略的收益是很不稳定的,与 VIX指数高度相关。市场恐慌时期的抄底行为是反转策略收益的最主要来源,因为此时提供的流动性最为宝贵,风险也最大。综合这两种理论即可发现,极端流动性风险因子和反转策略收益率高度相关,反转策略收益主要源于极端流动性风险因子剧变的时期,因此在控制了极端流动性风险因子后,反转效应不再显著。
(三)几种资产定价模型的对比
鉴于极端流动性风险因子在描述危机特征与补充风险溢价两个方面对传统流动性因子做了改进,以下我们尝试基于该因子构造新的定价模型,并与经典的定价模型进行对比。正如赵胜民等(2016)指出,因子定价模型的有效程度因市场发展水平和投资理念而异。中国股票市场存在明显的流动性驱动特征,且有较大的流动性波动性,这可能意味着考虑极端情况的流动性资产定价模型有更好的适用性。
我们分别将极端流动性风险因子加入CAPM和LCAPM中,构造了新的两因子模型(包含市场风险因子和极端流动性风险因子)和三因子模型(包含市场风险因子、流动性风险因子和极端流动性风险因子)。随后根据流通市值和账面市值比分组构建Fama-French的5×5组合。最后利用这25个组合,分别计算这两个新模型、LCPAM、Fama-French三因子模型以及 Fama-French五因子模型的 Gibbons统计量。较大的Gibbons统计量表明各组合截距项联合不等于零,该定价模型产生的 alpha越高,拟合程度越低,模型越差。该统计量的定义如下如式(6):
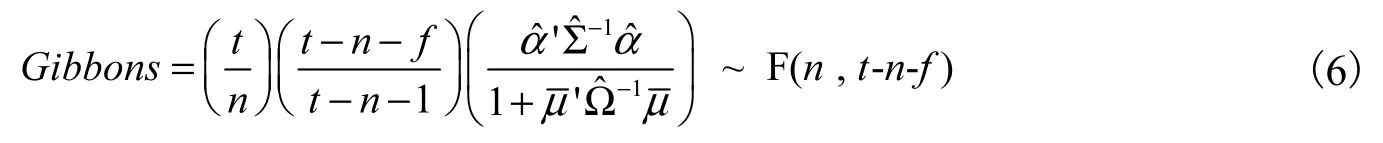
其中,t为时间序列期数,n为组合数,f为因子个数,为各组合截距项的列向量,为残差的协方差矩阵的无偏估计,为因子的样本均值的列向量,为因子的协方差矩阵的无偏估计,该统计量服从自由度为n和t-n-f的F分布。表4为本文所构造的两个新模型与 CAPM、LCAPM、Fama-French三因子模型和 Fama-French五因子模型的对比。
基于表4可得到以下结论。在各种期限下,加入极端流动性风险因子的模型都明显优于其他经典模型。将极端流动性风险因子加入CAPM和LCAPM后各有优劣,事实上极端流动性风险因子与传统流动性因子在正常时期的趋势是基本一致的,只有在危机时期才出现较大区别,出于模型简洁性的考虑,EL+CAPM 的形式是最优的。流动性模型的良好表现,说明中国股票市场流动性驱动的特征更为明显。加入极端流动性风险因子的新模型不仅符合流动性驱动的特征,也更好地描述了危机时的规律,故有更好的实证效果。

表4 几类资产定价模型的对比分析
五、市场层面的实证分析
(一)极端流动性风险因子与市场收益率
上文证实了极端流动性风险因子在横截面层面存在显著的风险溢价,那么该因子在市场层面是否存在同样的现象?该因子是否可以进一步加强对市场收益率的预测能力?下文在市场层面进一步展开检验。
Welch和 Goyal(2008)以及姜富伟等(2011)分别研究了美国和中国股票市场收益率的可预测性,认为估值水平、市值变化、股利水平以及通胀和货币供应量等宏观变量对市场收益率有预测作用。我们在姜富伟等(2011)所选定的变量基础上,加入了极端流动性风险因子。为了与 Kelly和 Jiang(2014)的结论进行对比,我们还在其中控制了极端收益率风险因子。
我们用流通市值权重和等权重方法重新计算了样本范围内的全市场收益率,并取5种不同的期限。结果显示,极端流动性风险因子对未来1个月到12个月的市场收益率具有解释能力;而在 12个月后,因子的解释能力逐渐减弱直至消失。此外我们还计算了极端流动性风险因子和极端收益率风险因子对解释市场收益率所贡献的比例。结果显示,极端流动性风险因子解释能力的比例约为 10%到 17%,与其他经典的预测变量基本相当,且在绝大多数形式下都高于 Kelly和 Jiang(2014)的极端收益率因子,说明了该因子的重要作用和在中国市场上的适用性。
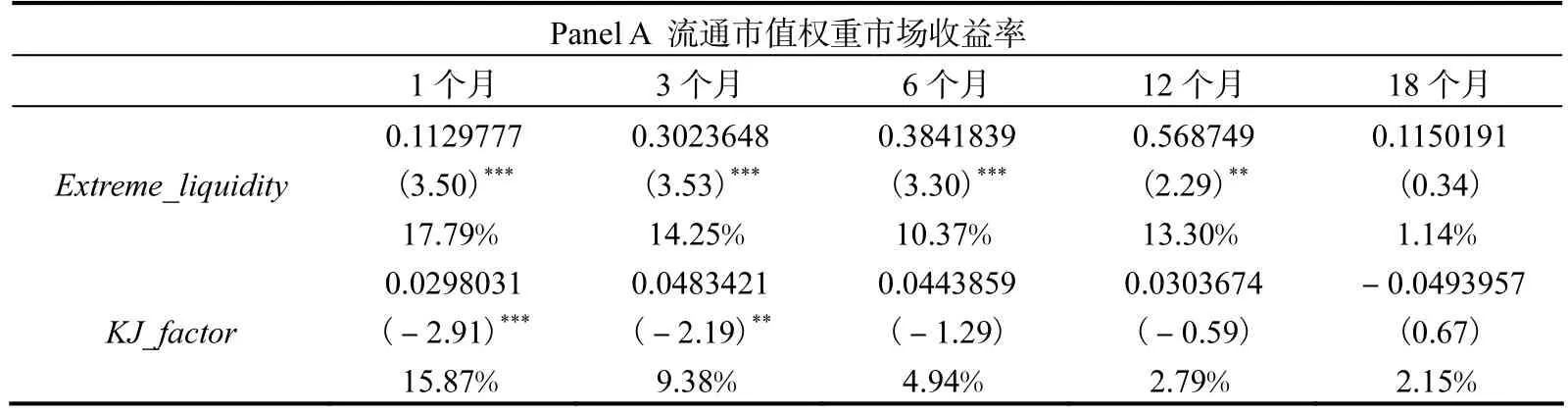
表5 极端流动性风险因子与市场收益率的回归分析

续表5
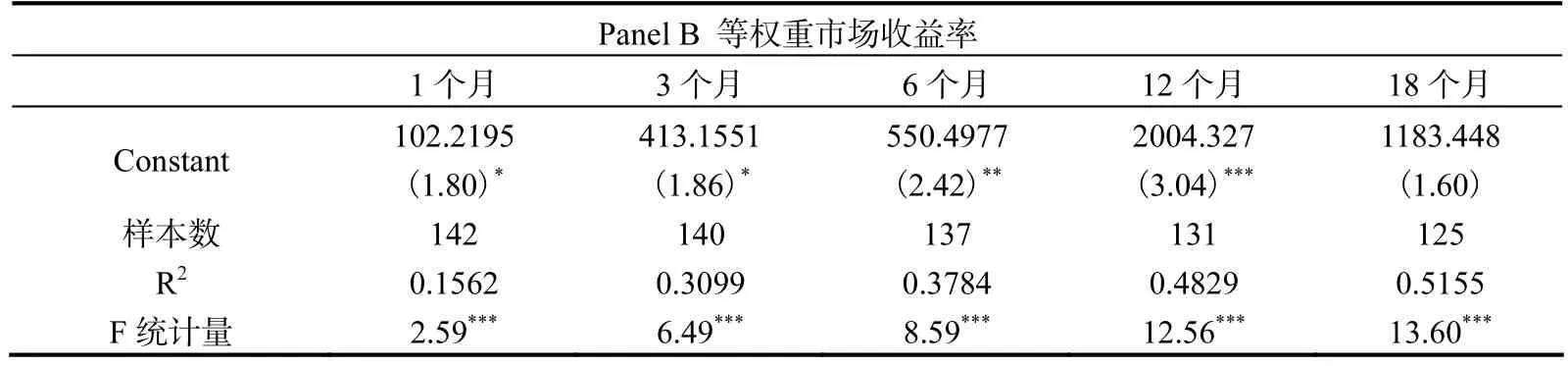
续表5
(二)极端流动性风险因子与宏观经济
参考 Kelly和 Jiang(2014)以及 Wu(2017)的研究框架,我们进一步探讨了极端流动性风险因子与一些宏观经济变量之间的联系。我们选择了总产出、固定资产投资、居民消费、通货膨胀、货币供应量和经济景气指数 6个宏观变量,建立 VAR模型①多数情况下的最优模型为VAR(3),个别为VAR(2)。,进行Granger检验,并求这些宏观变量对极端流动性风险因子冲击的脉冲响应图(图3)。
表6的结果显示,极端流动性因子是总产出、通货膨胀、货币供应和经济景气指数的Granger原因,表明极端流动性因子对这些变量有一定的领先和预测作用。

表6 极端流动性风险因子与宏观经济变量的Granger检验
图3的结果显示,极端流动性风险因子的冲击对多数宏观变量都存在影响②当然,这种影响只是单纯的领先滞后关系,并非因果关系。这种领先滞后关系反映了投资者的预期。。首先,极端流动性风险因子的冲击意味着总产出、固定资产投资和经济景气指数在1到2个月的短期下滑,并在6期之后基本收敛为零。其次,极端流动性风险因子冲击意味着未来 1到 4个月存在非常明显的通货紧缩和资金面紧张,并在 8期之后基本收敛为零。最后,居民消费的结果较为异常,极端流动性风险因子的冲击意味着未来1个月的居民消费增长,并在 3期之后基本收敛为零。我们认为,这一异常结果的可能原因有:从幅度上看对居民消费的冲击作用很小,且 Granger检验未通过,说明这种冲击并不显著;此外,由于极端流动性风险因子对危机有提前约1个月的指示性,此时市场仍处在最后的上涨期,仍然存在一定的财富效应,故居民消费在1个月后才出现拐点。

图3 宏观经济变量对极端流动性风险因子的脉冲响应图
极端流动性风险因子与各宏观变量之间的领先滞后关系表明,投资者对未来的预期可能是极端流动性出现波动并存在风险溢价的原因。以货币供应为例,投资者预期未来数月可能会出现资金面的紧张,对市场造成影响,故选择提前卖出资产。当市场狂热接近末期,投资者间的预期和交易行为趋同时,会优先选择卖出估值过高质量不佳的资产,出现“逃往质量(flight to quality)”现象,月内流动性观测的值的尾端显著增厚,极端流动性风险因子出现剧变。这种对未来宏观形势预期的自我实现,可能是该因子能够指示危机并存在风险溢价的深层原因。
六、稳健性检验
为进一步确保结论的可靠性,我们还进行了以下多组稳健性检验。
我们考虑引入一些与极端流动性风险相似的概念,考察极端流动性风险因子的解释力是否能够独立于这些研究。除正文中考虑的Kelly和Jiang(2014)的极端收益率风险指标外,我们进一步考虑了 Chen等(2001)、Hutton等(2009)、代冰彬和岳衡(2015)以及褚剑和方军雄(2016)的股价崩盘风险指标。股价崩盘风险同样反映了出现极端负收益率的可能性,近年来在学术界和实务界对此有极高的研究频率。股价崩盘风险指标的计算方法可参考 Chen等(2001)的负偏度系数(Crash_ns)与收益上下波动比率(Crash_ud)。首先应根据Hutton等(2009)的研究,按式(7)计算特质收益率。
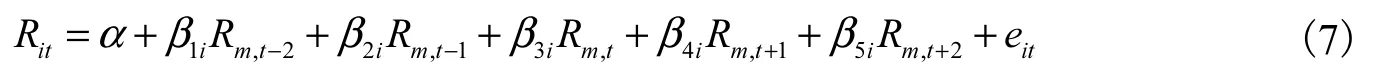
其中Rit和Rm,t分别为个股和市场的日收益率①引入市场收益率的提前和滞后期是为调整非同步交易的影响。Chen等(2001)以及Hutton等(2009)是基于周度数据计算年度股价崩盘风险,而本文的频率更高,故非同步交易的调整更为重要。,回归所得残差即为特质收益率rit。随后,可根据式(8)和式(9)计算负偏度系数和收益上下波动比率。
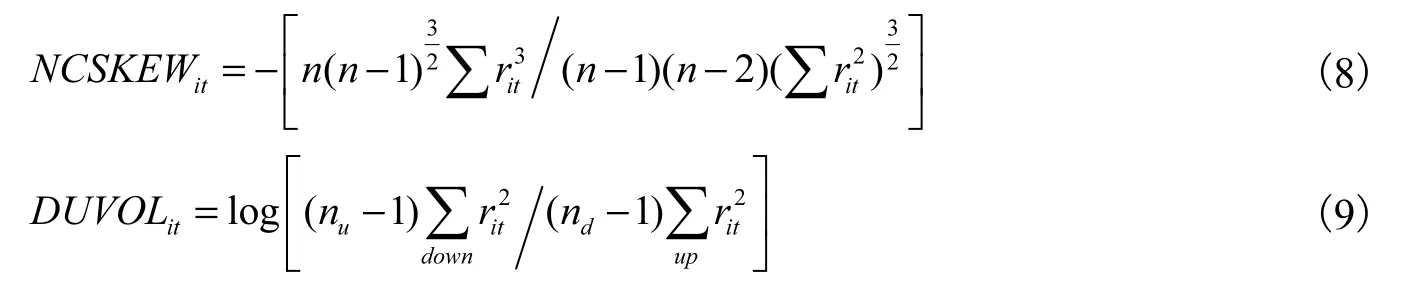
其中nu和nd分别为月内上涨和下跌的天数。
我们引入 Crash_ns以及 Crash_ud指标重复了表2的回归。表7的回归结果显示,控制这些变量并不影响极端流动性风险因子的显著性。
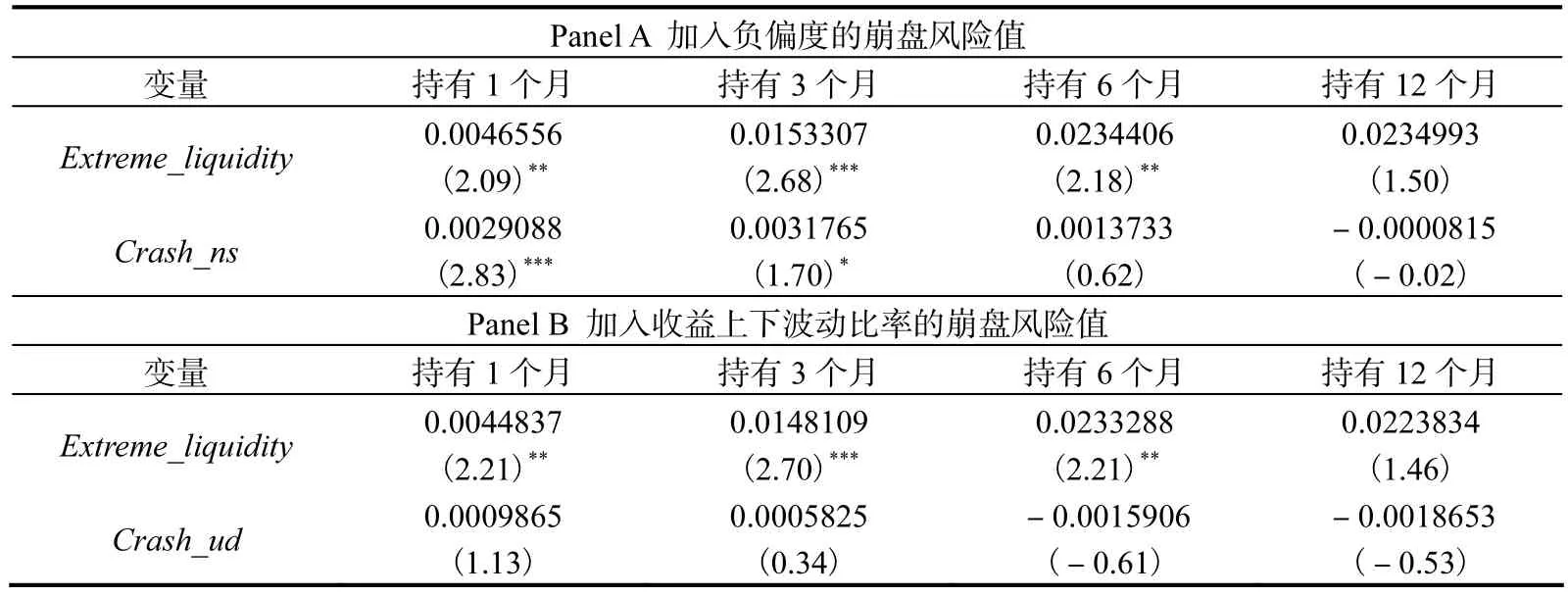
表7 加入类似指标后极端流动性风险因子beta与个股收益率的Fama-MacBeth回归分析
此外,我们还尝试了不同的极端流动性风险因子 beta值的计算方法。首先,我们采用滚动60期计算beta,此时得到的beta值更为稳定,但也包含了更多的陈旧信息。其次,我们提高了流动性尾端的阈值标准,将其设定为 99%,并重新计算极端流动性风险因子与其beta值。最后,我们在beta计算时与Fama-French三因子同时进行多元回归。表8的结果显示,各类beta值的计算方法基本不影响本文的结果。
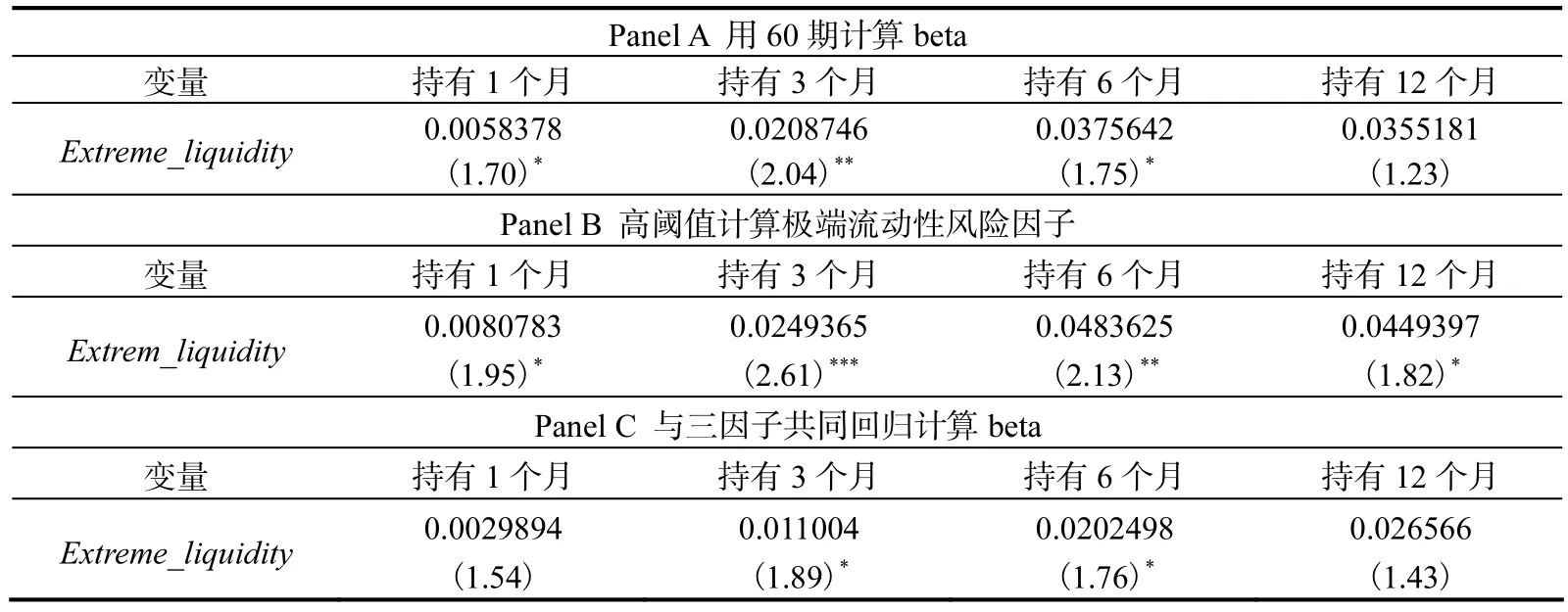
表8 其他beta计算方法下极端流动性风险因子beta与个股收益率的Fama-MacBeth回归分析
七、结 论
2015年到 2016年中国股票市场的流动性枯竭,给学术界和实务界都带来了深刻的冲击。然而,传统理论中的流动性资产定价模型并不能很好地预测和解释这次大规模的流动性恐慌。本文基于这一出发点,结合次贷危机以来的最新研究成果,认为传统的流动性因子存在两个缺陷。一方面,危机时期的流动性打破了均值回复性,呈现出自我强化加速下滑的特征,传统的流动性因子无法描述危机时期的特殊性质。另一方面,投资者存在“惊弓之鸟”的特征,对危机可能出现的恐惧,即使在正常时期也存在显著的风险溢价,传统的流动性因子遗漏了这部分风险溢价。为解决以上问题,本文将Kelly和 Jiang(2014)以及 Wu(2017)的框架进一步推广到了中国股票市场流动性中,基于幂律分布假设和 Hill估计量,构造了极端流动性风险因子,在以上两个方面扩展了传统的流动性资产定价模型。
在实证检验中,本文得到了以下结论。第一,极端流动性风险因子相较于传统的流动性因子在市场流动性恐慌期显著增大,且有约一个月的提前期,对重大的危机具有提前指示作用。第二,极端流动性风险因子在横截面上存在显著的风险溢价,且可以消除传统资产定价模型难以消除的反转效应异象。第三,将极端流动性风险因子与CAPM 的市场因子相结合构建的两因子定价模型,解释能力显著高于其他经典模型。第四,极端流动性风险因子对未来市场收益率有显著的预测能力,并对经典的市场收益率可预测性框架提供了补充。第五,极端流动性风险因子对未来宏观经济变量具有一定指示作用,极端流动性的冲击预示着未来 1个月的产出、投资和经济景气指数的下滑以及未来 4个月的通货紧缩和资金面紧张。这些结论表明,本文所构造的极端流动性风险因子在理论上扩展了流动性资产定价模型,深化了对危机时期流动性特殊性质的认识,也对投资实务有一定应用价值。
正如前文所言,资产定价模型的适用性取决于市场特征与投资风格。从本质上讲,中国股票市场上明显的流动性驱动特征和剧烈的流动性波动性,起源于明显的投机性特征,剧烈的股价波动并非由基本面引起,而是由短期投机性的资金流动引起。因此,定价模型的构建应充分考虑市场与投资者的特征,并非放之四海皆准,这也是本文结论有效的重要原因。

