基于多尺度方形Densenet的图像超分辨算法
崔浩翔
(深圳大学信息工程学院,广东 深圳 518060)
引言
在图像的应用当中,超分辨率是一个重要的研究方向,其主要思想是使用图像处理的方法由一幅低分辨率图像或图像序列恢复出高分辨率图像。这一思想于20世纪60年代产生,经过多年的发展,已经广泛应用于卫星遥感成像、医学影响、安防监控、数字媒体等诸多领域,成为这些领域中的关键技术。[1]
图像超分辨率按照重建信息获取的方式大致可以分为三类:(1)从低分辨图像自身获取信息的基于插值的方法;(2)从连续多帧图像中获取信息的基于重建的方法;(3)从外部样本库中获取信息的基于学习的方法。尤其在近些年来的研究当中,深度学习方法是一种重要的研究手段,它属于第三类研究方法,相比于传统的算法取得了更好的效果。[2]在这一类超分辨方法中,传统的CNN方法大都集中在单尺度层面进行研究,很难利用图像的多尺度信息,并且随着网络的加深,会由于梯度消失等问题产生网络收敛性变差的问题。[3]
针对以上问题,本文提出了一种多尺度方形DenseNet(MSRD)的图像超分辨算法。通过多尺度网络可以有效提取不同尺度的特征信息用于超分辨算法中的细节还原,通过稠密连接的方法可以有效地避免梯度消失的问题,并且可以提高网络中产生的特征图的利用率。实验表明,使用MSRD算法,可以带来比传统图像超分辨算法更好的效果。[4]
1 相关技术概述
1.1 图像的降质退化过程
在使用光学成像仪器获取图像时,由于种种原因,会产生变形(平移、旋转)、模糊(如运动模糊、光学模糊、散焦模糊)等问题,并且由于存储等原因的影响,高分辨率的图像会经过下采样,并且在传播过程中也不可避免地会受到噪声的影响,最终成为低分辨率图像。整个过程可以表示为:
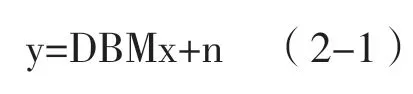
其中,x为高分辨率图像,y为低分辨率图像,M为几何运动矩阵,B为模糊矩阵,D为亚采样矩阵,n为噪声。如图1所示为图像的一般降质退化过程。
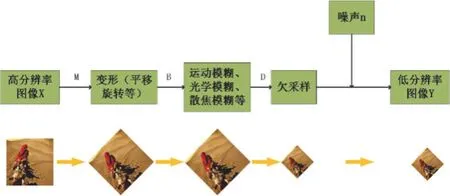
图1 图像的降质退化过程
1.2 SRCNN
SRCNN是一种经典的图像超分辨算法,其网络结构如图2所示。
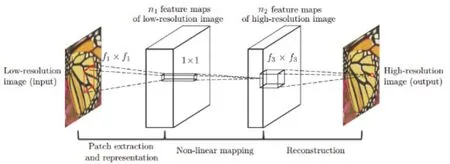
图2 SRCNN的网络结构图
SRCNN的输入图片为低分辨率图片,在输入之后会使用双三次插值将低分辨率图片放大到目标尺寸,之后输入网络进行卷积操作,最终得到与高分辨率图片同尺寸的输出图片。SRCNN中包含了3个卷积层,其卷积核大小分别为9×9,1×1和5×5,分别进行特征提取、特征非线性映射和图像重建。
SRCNN是深度学习算法应用于图像超分辨领域的经典算法,使用这种算法可以取得不错的性能。但是SRCNN网络较为简单,只能提取单尺度特征,并且在加深网络深度后会出现梯度消失的问题。
1.3 图像超分辨率的客观评价指标
图像质量客观评价指标是通过数学计算方法得到的,通常使用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)和结构相似性(structural similarity index,SSIM),结构相似性来度量图像的客观质量。
PSNR的定义如下:

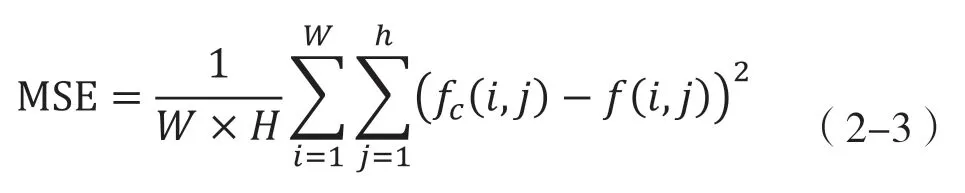
式中,w和h分别为图像的宽和高;fc (i,j)和f(i,j)分别为处理后的图像和原图像在对应点的像素的值。一般来说,PSNR越大则图像质量越高。但是PSNR并不与图像质量一一对应,即使是同样的PSNR所对应的图像可能视觉观感完全不同。比如说,在很亮或细节很多的区域的加性噪声非常不明显,但是同样的噪声如果出现在暗或平滑的区域就易于被察觉。这主要是由于人的视觉系统对于不同情况下的亮度或者细节的敏感度不同,但是PSNR与图像本身的亮度和细节无关,而只与亮度变化的程度有关。另外,同样的PSNR,如果噪声是均匀分布于图像之中,人们并不易于察觉这些噪声,但是如果集中分布,则非常的显眼。
SSIM的定义如下:
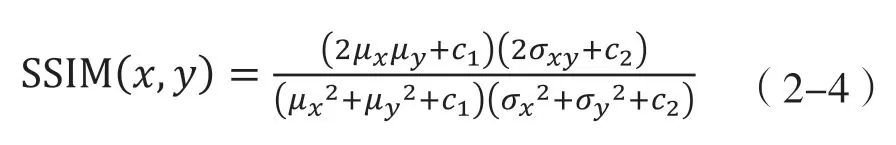
2 基于多尺度方形Densenet的图像超分辨算法MSRD
2.1 MSRD的网络结构
常用的获取多尺度信息的方法主要有两种:(1)使用下采样等手段获取不同尺度的输入图片,再缩放到同一尺寸用于图像处理;(2)将不同尺度的特征图缩放到同一尺寸用于图像处理[5]。MSRD采用第一种方法提取多尺度信息,其网络结构如图3所示。
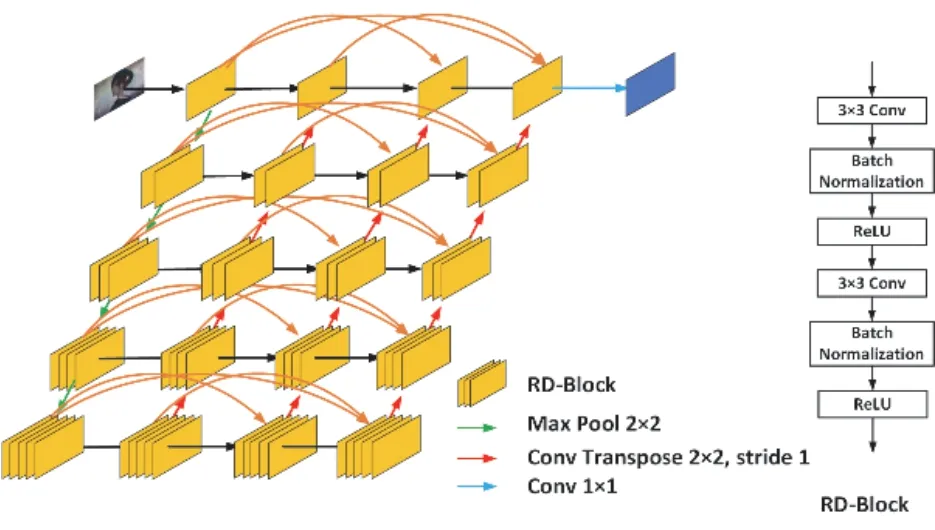
图3 MSRD的网络结构图
MSRD中使用下采样的方法获取不同尺度的图片,通过多次的卷积操作可以逐步提取不同尺度的图片中的特征信息,低层网络中包含更多的细节性能,而高层网络中则包含更多的环境信息。
在MSRD中不同尺度的图像会包含不同层级的特征信息,在每一层中需要通过多次的卷积操作提取不同层次的特征信息,为了避免随着深度的增加而产生的梯度消失问题,我们采取了稠密连接的方式,从结构图中可以看到,每层网络都是一个DenseNet,这样做可以有效地提高特征的利用率,有效缓解梯度消失的问题。
2.2 MSRD的卷积单元
MSRD中的卷积单元RD-Block如图4所示。
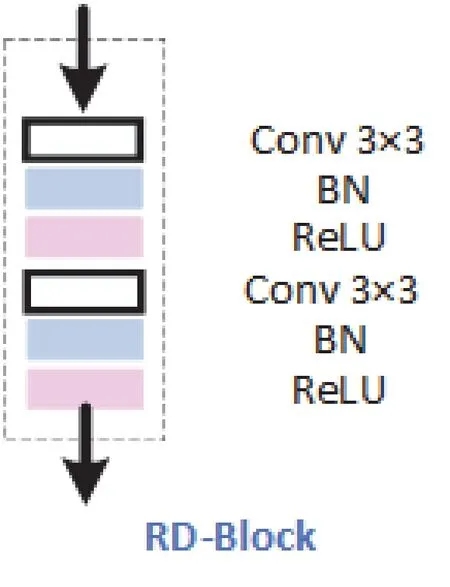
图4 MSRD中的卷积单元
RD-Block中包含2个卷积层、2个BN层和2个ReLU层,卷积层中的卷积核大小为3×3,在每次卷积之后都加入了BN层和ReLU。使用BN层可以改善流经网络的梯度,其次在训练过程中还允许更大的学习率进而大幅提高训练时的收敛速度,再次使用BN层可以减少网络对于初始化的强烈依赖,并且减少了对于dropout的需求。
2.3 MSRD的“剪枝”特性
MSRD的网络结构较为复杂,运算量较大。针对这一问题,我们可以使用MSRD的“剪枝”特性来自适应地降低计算复杂度,如图5所示[6]。
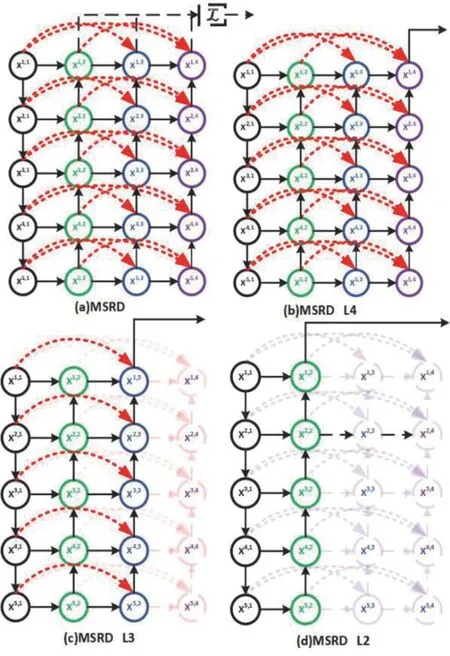
图5 MSRD的“剪枝”特性示意图
MSRD具备“剪枝”特性,在较为简单的应用当中可以使用低级的网络,而在较为复杂的应用当中,则可以使用较为高级的网络,基于这一特性可以在保证网络性能的情况下降低运算量。
3 实验分析
3.1 数据库
本实验所用数据库为BSDS-300数据库,其中包含训练集和测试集,如表1所示。

表1 图像超分辨实验数据
为便于实验的进行,在训练时我们将图像进行中心裁剪,在图片的缩小比例为2x和4x的实验当中,我们将patch size取为256×256,在缩小比例为3x的实验中,我们将patch size取为192×192。
3.2 实验环境
我们的实验环境为一台Linux服务器,系统版本为ubantu 16.04,我们所使用的深度学习框架为Pytorch,其版本为0.3.0.past4,使用nVidia Tesla K80进行GPU加速。
3.3 损失函数
本实验使用的损失函数为基于均方误差的损失函数,其公式为:
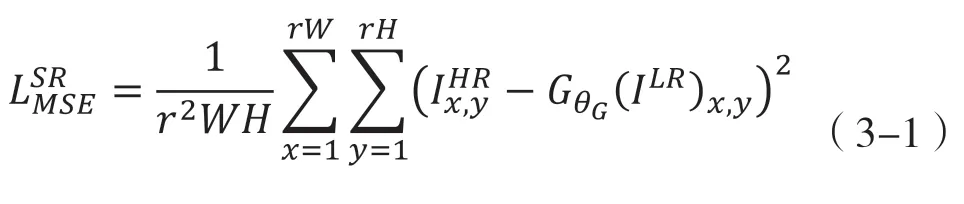
3.4 实验方案
在训练时,我们将数据集中的图片经过下采样取得缩放比例为2x、3x、4x的图片,将其作为输入图片,将原图片所谓目标图片,网络的输出结果为4、9、16通道的输出图片,最终将输出结果还原为原分辨率的图片进而计算其损失进行反向传播。
实验中所使用的MSRD的深度为6层,层数为3层,同时我们使用SRCNN、U型多尺度CNN(U-Net)作为平行对照网络,实验中使用的U-Net为3层。实验中所使用的学习速率为并在迭代80次后将学习速率调整为实验使Adam优化器,迭代次数设定为100代,batch size设定为16。使用训练集进行训练,并在每代之后将测试集数据输入网络,通过PSNR和SSIM来反映网络性能。
3.5 实验结果
我们训练的迭代次数设定为100,训练结束后,我们比较了双线性插值、SRCNN、U-Net和MSRD算法的PSNR、SSIM和测试时间等指标,我们在测试集中取出了Tiger、Talking、Airplane、Elephant等图片进行测试分析,所得结果如表2所示。
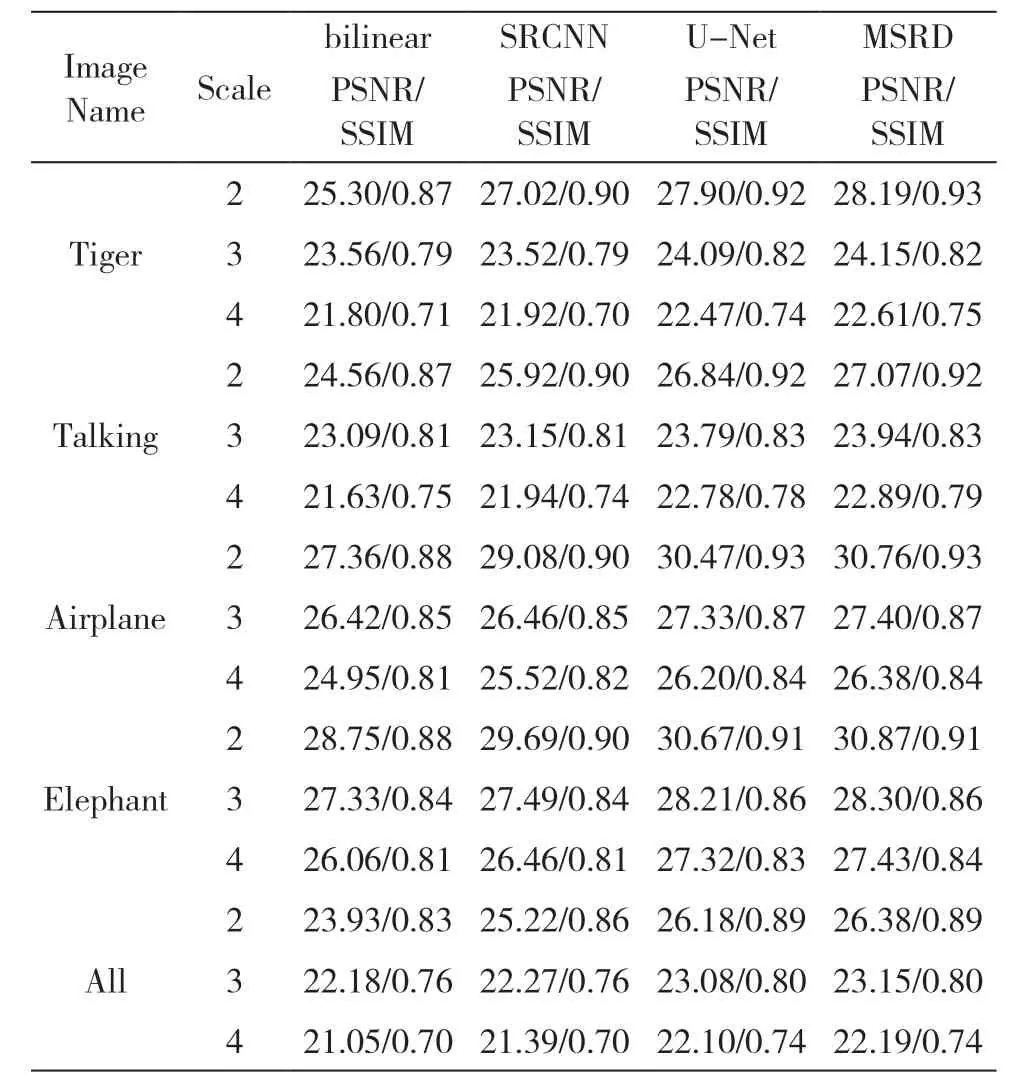
表2 图像超分辨实验结果
从表2中可以看出,相比于传统算法中的双线性插值方法,深度学习方法的性能非常突出。在2x、3x、4x比例的实验中,SRCNN在PSNR指标上比双线性插值高出1.29dB、0.11dB、0.34dB。而U型多尺度CNN网络U-Net相比于SRCNN分别在2x、3x、4x中PSNR指标高出0.96dB、0.81dB、0.71dB,说明在使用多尺度网络提取多尺度特征进行图像超分辨重建任务可以带来更高的性能提升,多尺度特征对于指导图像的修复起着至关重要的作用。MSRD相比于U-Net分别在2x、3x、4x中PSNR指标高出0.2dB、0.07dB、0.09dB,说明稠密连接方法对于图像超分辨研究确实有性能的提升。另外,图像超分辨任务中,SSIM指标的提升并不明显,因为图像超分辨任务中,下采样获取的低分辨率图片依旧可以很好地保留图像的结构信息,另外使用MSE作为损失函数会得到更好的PSNR指标,而对于SSIM指标的提升也并不突出。
由于MSRD的网络结构较为复杂,会提高网络的计算量,因此MSRD可以利用其“剪枝”特性自适应的调整网络的深度,在保证网络性能的前提下降低网络的计算量。我们在训练时,定义了多尺度损失函数,在网络中的输出端使用多个损失函数进行监督,提取出不同级别的输出结果,我们将2x图像超分辨任务的结果表示在图6中。

图6 超分辨率实验结果图 (a)双线性插值 (b)SRCNN实验结果 (c)U-Net实验结果 (d)MSRD depth=2实验结果 (e)MSRD depth=3实验结果 (f)MSRD depth=4 实验结果 (g)MSRD depth=5实验结果 (h) MSRD depth=6实验结果
根据上图可以明显看出,在增加多尺度损失函数后,各级MSRD的输出结果均表现良好,深度为2、3、4、5、6层的MSRD相比于SRCNN网络在PSNR上分别高出1.46dB、1.59dB、1.56dB、1.64dB、1.68dB,说明MSRD相比于SRCNN性能提升非常明显。而MSRD中PSNR指标最低的深度为2的网络模型依旧比U-Net网络高出0.07Db,而深度为6的网络模型则高出U-Net0.29dB,说明稠密连接的思路对于超分辨率算法的提升非常明显。由于低层网络的网络参数较少,计算复杂度远低于高级网络,因此在较为简单的应用场景中可以使用较为低级的MSRD网络,其性能依旧高于传统的图像超分辨算法。
4 结论
本文提出的基于多尺度方形DenseNet的图像超分辨率算法相比于传统算法具有很好的性能,这种网络是在多尺度CNN网络模型的基础上加入了稠密连接的思想,相比于传统的图像超分辨算法在不同的缩小比例中可以在PSNR上有超过0.8dB的提升,另外MSRD可以在不同场景中根据其“剪枝”特性来降低其计算量,保证运算速度。

