基于叠栅的Bragg光纤光栅综合方法的研究
张宝荣,黄 震,张玉唯
(1. 燕山大学 信息科学与工程学院, 河北 秦皇岛 066004;2. 河北省特种光纤与光纤传感重点实验室, 河北 秦皇岛 066004)
引言
已知光纤光栅结构求解其反射谱是大家熟知的问题[1],其逆问题即是在给定一个光纤光栅反射谱的情况下求解光纤光栅结构的问题,也称为光纤光栅的综合问题。目前已经有多种解决光纤光栅综合问题的方法, 最早的精确综合方法是基于Ge’fand-Levitan-Marchenko(GML)积分方程的逆散射算法[2],被广泛应用于色散补偿器的设计[3]。对于弱耦合光纤光栅,光栅的综合问题可以根据一阶波恩近似简化为光栅反射系数的傅里叶逆变换,该方法适合于光栅的反射功率比较小的情况[4]。在此之后,基于信号处理技术[5]和微分逆散射算法[6-7]的综合方法也被提出来。1999年由R.Feced, M. N.Zervas根据因果关系提出的层剥离光栅综合算法大大降低了算法的复杂性[7],该算法的优势在于它直接利用光栅分析中的耦合模方程来解决问题[8-10],整个综合过程透明化,使得光栅综合问题变得相对简单了。综合得到的光栅切趾函数一般都比较复杂,直接制作这样的光栅对制作工艺要求很高,实现困难。因此寻找易于实现的光纤光栅综合方法很有必要。
光纤叠栅是指在同一段光纤上重复刻写多个Bragg光栅[11],这些Bragg光栅的参数在刻写过程中可以分别进行控制,光纤叠栅的反射光谱是多个Bragg光栅的反射光谱的线性叠加[12-13], 光纤叠栅扩展了光纤光栅的许多应用[14-15]。
提出将layer-peeling光栅综合算法和Bragg光纤光栅叠栅方法相结合,得到一种新的Bragg光纤光栅综合方法。首先根据需要的反射光谱,利用层剥离综合算法得到Bragg光纤光栅折射率包络分布函数(切趾函数),然后利用多个高斯切趾函数叠加来拟合出这个折射率包络分布函数,这些切趾函数就是光栅叠栅中各个Bragg光栅的切趾函数,按照这样的切趾函数制作叠栅,其反射光谱既是所需要的。相对一般的复杂切趾函数,高斯切趾函数对于光栅的写入是易于实现和控制的。
1 层剥离光栅综合算法
在求解Bragg光纤光栅反射谱问题的过程中,在构想和概念上可能会有所不同,但是基本上都是等同于求解线性常微分方程组,即光纤光栅耦合模方程组。由于Bragg光纤光栅是一种反射型光栅,光栅中的模式只有前向和反向传输模式的耦合,所以为了简便,根据文献[8,9]我们选择如下形式的方程组:
(1)
(2)
式中:a(z,δ)和b(z,δ)分别是前向传输光模式和反向传输光模式的复振幅;q(z)是光栅包络函数用来描述Bragg光纤光栅的切趾函数和啁啾信息;失谐量δ与入射光波长λ和Bragg波长λB关系如下:
(3)
求解耦合模方程组需要光纤光栅的边界条件,在光栅的结束区域即z=L处,a(L,δ)=a0和b(L,δ)=0。沿着光栅长度z的反方向解耦合模方程,在z=0处,解得a(0,δ)和b(0,δ),则光栅反射谱r(δ)为
(4)
在反向传播过程中,可以定义光纤光栅的局部反射谱r(z,δ)为
(5)
层剥离光栅综合算法的过程如下:在光栅的起始区域,我们给定初始的光栅反射谱为r(δ),假定a(0,δ)=1,依据(5)式,则b(0,δ)=r(δ)。已知a(0,δ)和b(0,δ),则可以求出初始位置的q(0),求解使用以下积分公式[8]:
(6)
该式是层剥离光栅综合算法中的综合关系。将a(0,δ)、b(0,δ)和q(0)带入到耦合模方程(1)式和(2)式中,利用龙格库塔数值方法可以求解出下一个z值所对应的a(z,δ),b(z,δ)和r(z,δ)。再根据(6)式就可以求出相应的q(z)。按照此迭代过程,沿着z增长取值,可依次求得局部反射谱r(z,δ),进而可以求得在整个光栅长度范围内的光栅包络函数q(z)。用此光栅包络函数q(z)切趾Bragg光纤光栅,就可以得到相应的反射谱,该反射谱就是我们最初给定的r(δ)。
在计算过程中,主要的误差来源有2个:1)在综合关系中,积分数值计算会造成计算误差项;2)在耦合模方程的求解过程中,步长Δz的大小是有限的,会产生传播误差。数值积分计算误差项,主要依靠于失谐量δ的分辨率,同时还取决于失谐量的取值范围。要保证失谐量的分辨率和宽度具有一定的精确度,通常需要初始反射谱具有适合的频谱宽度和精细的结构。对于传播误差项,可以通过调整计算步长进行检测,以减小该误差项的影响。
2 基于叠栅的综合方法
Bragg光纤光栅叠栅可以由多个重叠写入的Bragg光栅构成,这些重叠写入的Bragg光栅可以从相同或是不同的起始点写入,可以拥有相同或是不同的光栅周期和光栅长度,同时还可以给这些Bragg光栅加入切趾和啁啾。在一段光纤上,Bragg光纤光栅叠栅的折射率分布可以表示为
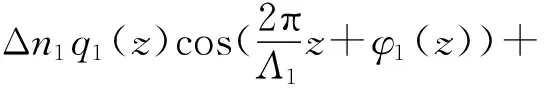
(7)

(8)
则(7)式进行整理得到:
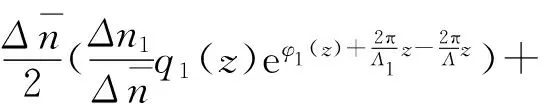
(9)
即,
(10)


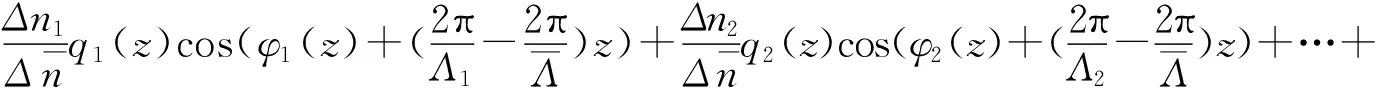
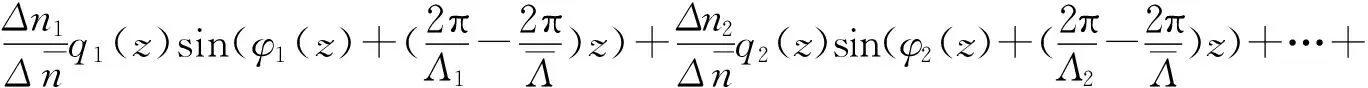
根据(9)式可以推导出叠栅耦合模方程中的包络函数,该包络函数是一个复数,其模值表示的是叠栅的切趾信息,其相位则表示叠栅的啁啾信息。
应用层剥离光栅综合算法求出包络函数q(z),为得到给定的反射谱,需要用q(z)作为包络函数,在实际操作过程中,由于q(z)函数可能不是常规函数,在刻写光栅过程中,很难控制非常规切趾函数的刻写,这就使得层剥离光栅综合算法的实际应用价值降低。
由(9)式可知,只要叠栅数目m足够大,层剥离光栅综合算法求得的包络函数q(z)都可以用m个叠栅的切趾函数拟合出来,因此用m个Bragg叠栅就可以实现想要的反射谱。在实际应用中,在一段光纤上重叠刻写多个不同参数的Bragg光栅相比于刻写具有特殊包络函数的光栅更容易实现,因为叠栅中每个光栅都是独立刻写的,依次写入。
3 例子仿真分析
为了检验上述理论分析结果,用2个例子来分析这种方法的可行性及误差。例子1是高斯型反射谱作为目标谱:
(11)
若取中心波长1 550 nm,半峰全宽0.3 nm,整个反射带内零色散为零,即d2φ(δ)/dδ2=0。假定φ(δ)=0.8δ+0.5,给定失谐量的范围δ=±50。则方程(11)对应的反射谱形状如图1所示。采用四阶龙格库塔法对方程(1)和(2)进行数值解析,利用辛普森积分法则解方程(6),在两种运算中分别取步长Δδ=0.005和Δz=0.005 cm,光栅长度z=3 cm。求出相应的包络函数q(z),如图2所示。

图1 高斯型反射谱(目标谱)

图2 Layer-peeling算法的综合结果q(z)
6个高斯型f(z)=Ae-(z-zc)2/w2函数就可以很好地拟合出包络函数q(z),结果见图3,拟合过程都是利用Origin8的多峰拟合完成的。表1是6个高斯切趾函数Bragg叠栅的参数,周期Λ=538.2 mm。

表1 高斯切趾叠栅参数

图3 6个高斯函数拟合的包络函数q(z)
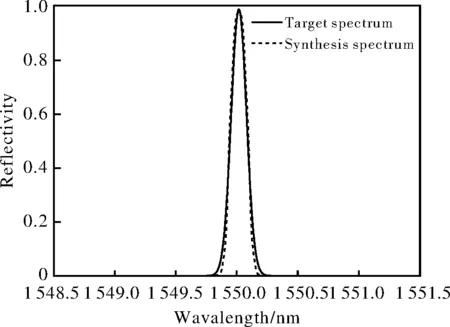
图4 高斯型目标谱与综合谱对比
从图4可知,利用基于叠栅的Bragg光纤光栅综合算法求得的反射谱与目标谱形状大致相同,峰值大小和半高全宽基本相同,数值计算综合谱与目标谱的相对误差约为0.82%。
对于某些光纤光栅的特殊应用,有时候会要求反射谱形状是三角型或者近似三角型,在其它光纤光栅解调的应用中也能用到[16-17],因此综合出三角型光栅反射谱是具有实际意义的。图5是目标谱,图6是层剥离算法的综合结果,包络函数为q(z)。
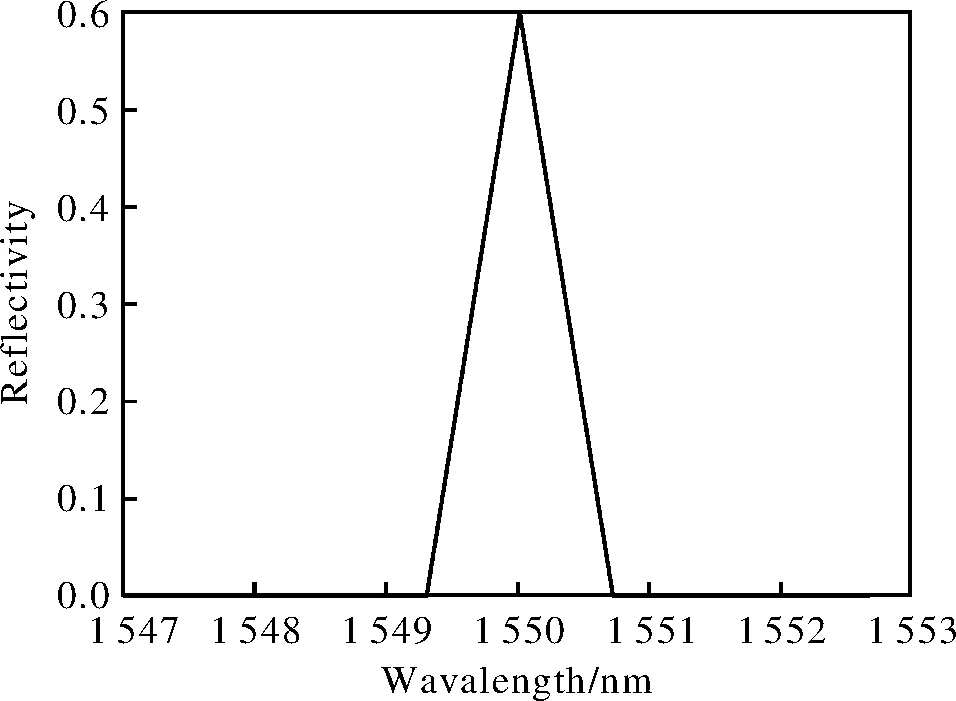
图5 三角型反射谱(目标谱)
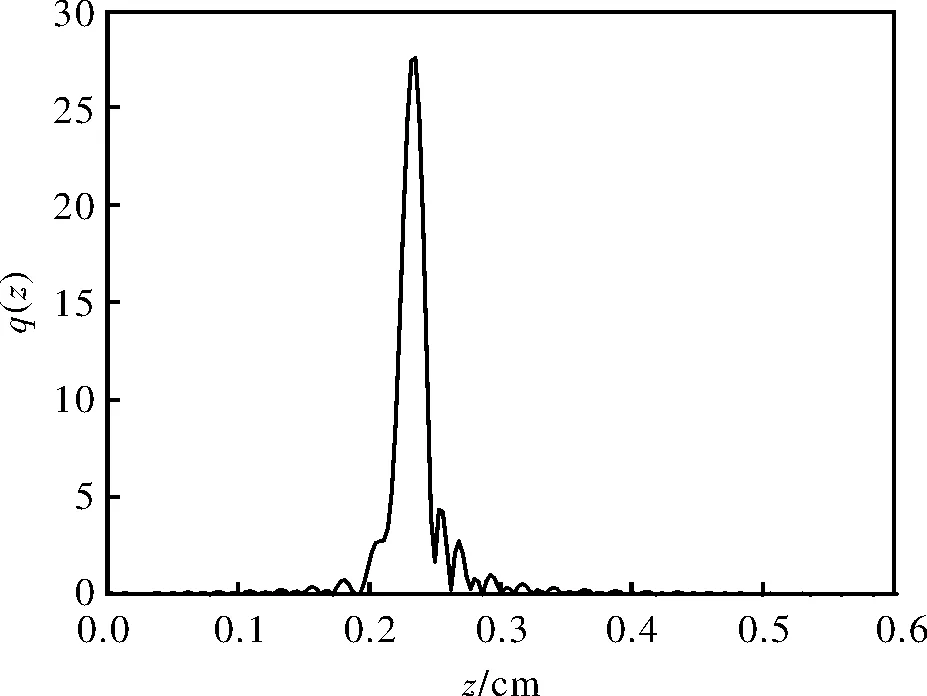
图6 Layer-peeling 算法的综合结果q(z)
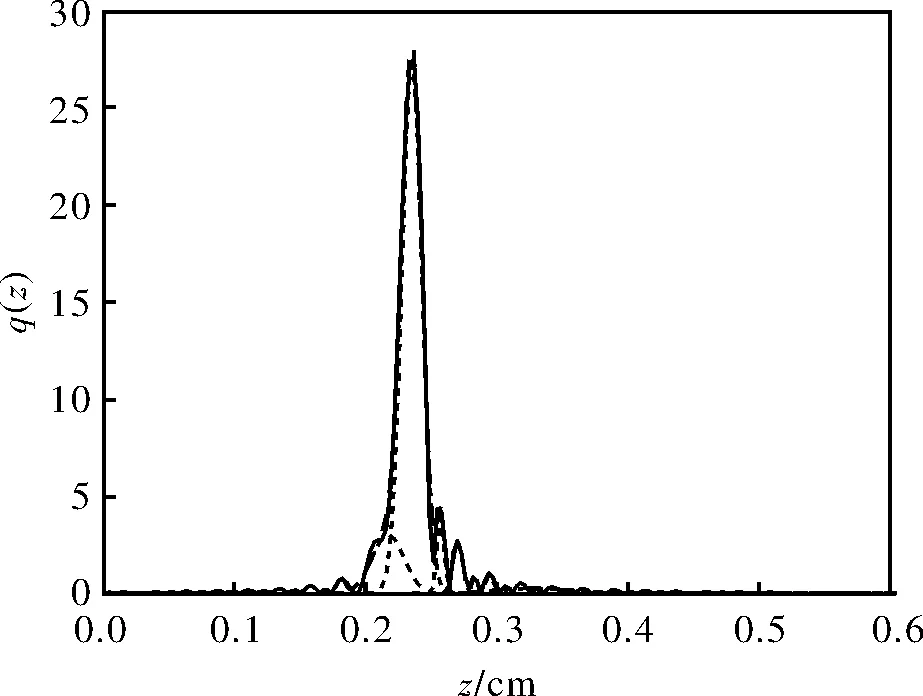
图7 8个高斯函数拟合的包络函数q(z)

图8 三角型目标谱与综合谱对比
给定光纤光栅长度为3 cm,光栅周期为538.2 nm,有效折射率为1.44,反射谱峰值设定为0.6, 如图8所示即为综合光栅反射谱与原三角型反射谱对比图。观察图8可知,由基于叠栅的光纤布拉格光栅综合算法求得的光栅反射谱图形与原三角型目标反射谱相比,其形状大致相同,但是综合得到的反射谱图形在波峰上升起点早于目标谱,下降终点晚于目标谱,上升开始处和下降终点处相比于目标谱有所缓和,没有目标谱变化急速。除此之外,综合谱的峰值和半高全宽基本与目标谱相同,数值计算综合谱与目标谱的相对误差约为3.92%。
4 结论
用光纤叠栅来可以实现一定目标谱的光纤光栅的综合,通过数值计算验证了这种方法的可行性,用高斯函数作为切趾函数,只需要少量的叠栅就可以实现具有特定切趾函数的光纤光栅,2个例子的计算结果表明,综合叠栅得到的反射谱与目标谱基本一致,相对误差小于4.0%。其他切趾函数的叠栅也有待进一步的研究。

