基于BQGA-ELM网络在滚动轴承故障诊断中的应用研究

皮 骏， 马 圣， 杜旭博， 贺嘉诚， 刘光才

(1.中国民航大学 通用航空学院，天津 300300；2.中国民航大学 航空工程学院，天津 300300)

在实际工程中，无论地面机械设施还是航空航天工业中所涉及的转子机械，在长期的使用过程中会出现机械故障，尤其是转子机械的轴承故障。如：航空发动机四号轴承，由于它所处的位置特殊，因此对它进行监控诊断难度较大。为了更好的解决这些问题，需要对故障诊断方法进行研究[1-2]。旋转机械中的轴承性能状态，将直接影响到机械设施能否正常有效的工作[3]。但由于轴承寿命离散度较大，因而广泛引起国内外诸多学者的重视。

随着对转子动力学[4]的深入研究，根据物体的振动信号亦能诊断故障。这种方法避免了人为因素的干扰，但对振动信号的准确提取提出严苛的要求[5-6]。在信号采集、处理等过程中，故障振动信息的部分特征可能会丢失，这就造成了信号的模糊性。由于部分智能算法具有模糊识别的能力，即使故障振动信号的提取不是绝对准确，也能得到较好的诊断结果。因此在文献[7-10]中，学者利用不同的信号处理手段对轴承故障振动信号进行处理，并分别结合支持向量机[11]、多核学习机[12]、人工神经网络[13-14]、Elman[15]网络和RBF[16]网络对轴承故障进行诊断，并取得较好的成果。虽然这些学者运用部分神经网络在诊断中得到较好的结果，但由于部分神经网络收敛速度较慢、易陷于局部最优，因而得到的结果仍有提升的空间。

针对部分前馈型神经网络存在的缺陷问题，Huang等[17]人提出了极限学习机神经网络(Extreme Learning Machine,ELM)的概念。ELM避免了传统前馈神经网络对学习速率、终止条件、易陷于局部极优等缺陷，因而广泛用于数据压缩、特征学习、聚类、诊断等领域。近年来，ELM网络被运用到航空发动机、机械等诸多领域的故障诊断中，同时得到了比部分前馈神经网络更好的诊断结果。虽然ELM网络的优势明显，但它相比传统神经网络可能需要更多的隐含层神经元数量，且随机赋予输入权值和阈值，可能会导致病态问题出现[18]。因此，部分学者提出用智能优化算法对网络进行优化，如：卢锦玲等[19]利用改进粒子群算法和交叉验证优化极限学习机，并将优化的学习机用于轴承故障诊断；徐继亚等[20]利用鲸鱼算法优化极限学习机，并用于轴承故障诊断；Yang等[21]利用量子粒子群算法优化极限学习机，并对航空发动机故障进行诊断；Lu等[22]引入传感器故障失效率改进ELM网络，并用于传感器的故障诊断与重构。但GA(Genetic Algorithm)和PSO(Particle Swarm Optimization)等优化算法均存在一些缺陷[23]，所以用来PSO和GA优化ELM网络不能得到很好的效果。针对ELM网络缺陷和轴承故障诊断问题，本文提出Bloch球面量子遗传算法优化极限学习机网络作为滚动轴承故障诊模型。

量子遗传算法[24]是在传统的GA中引入量子并行计算，极大地加快了算法对信息的处理速度。与传统的GA不同的是，量子遗传算法(Quantum Genetic Algorithm，QGA)用量子比特取代传统遗传算法中的二进制染色体；QGA采用量子门操作更新种群，能够对空间进行有效搜索；同时采用量子位的平面坐标进行染色体编码，使得染色体数量为单一编码的二倍，因而增加种群的多样性。但量子遗传算法也存在部分缺陷，如：频繁的二进制解码、量子旋转方向基于查表等。针对QGA存在的这些问题，Pan[25]提出的Bloch球面量子遗传算法(Bloch QGA, BQGA)，BQGA比QGA拥有更好的多样性和收敛性特征，且具有良好的空间搜索能力。在Bloch球面量子遗传算法中，通过相位翻转实现量子染色体的变异，从而能够有效地保持种群的多样性。因此，本文使用Bloch球面量子遗传算法优化极限学习机网络的输入权值和隐含层阈值，再用Moore-Penrose算法计算ELM网络的输出权值矩阵，最后使用优化的ELM网络对滚动轴承故障进行诊断。

1 极限学习机相关理论模型

Huang等提出极限学习机网络，ELM网络随机赋予输入权值和阈值，便能逼近任意非线性分段函数[26]。设ELM网络输入层有n个神经元，隐含层有l个神经元，输出层有m个神经元，则ELM网络的输入权值矩阵表示为

(1)

式中：ωij为输入层第i个神经元与隐含层第j个神经元间的连接权值。记隐含层与输出层之间的连接权值矩阵为

(2)

式中：βjk为隐含层第j个神经元与输出层第k个神经元间的连接权值。设隐含层神经元的阈值矩阵为

(3)

若存在Q个有效样本，其输入矩阵X和输出矩阵T分别为

(4)

若ELM网络隐含层神经元激活函数为g(x)，则Q个有效样本输出矩阵T中的任意元素tmQ可由式(5)计算

(5)

因此，输出矩阵T的计算可简记为

Hβ=T′

(6)

式中：H为ELM网络隐含层输出矩阵；T′为ELM网络输出矩阵T的转置；β为ELM网络输出权值。输出权值β可由最小二乘法求得

(7)

式中：H+为输出矩阵H的Moore-Penrose广义逆。由于最小二乘法能求得唯一解，因此ELM网络使用Moore-Penrose广义逆能够极大的提高学习效率。

文中所用到的隐含层激活函数为

(1)Sigmoid()函数

(2)Sin()函数

f(a,b,x)=sin(ax+b)

(3)RBF()函数

f(a,b,x)=e(-b‖x-a‖2)

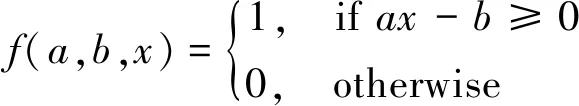
2 基于Bloch球面量子遗传算法优化的ELM网络(BQGA-ELM)

2.1 优化过程描述

极限学习机网络相比传统神经网络可能需要更多的隐含层神经元，且由于随机赋予输入权值和阈值，可能会导致病态问题出现。因此，针对这一问题，本文提出使用Bloch球面量子遗传算法优化ELM网络，并应用于滚动轴承故障诊断之中。则BQGA优化ELM网络的流程图如图1所示。

BQGA-ELM的具体步骤如下：

步骤1设置相关参数，包括种群大小、迭代步数、相位旋转步长等；

步骤2Bloch球面上的某一点P，给定相位角θ和φ便可表示为|φ〉=[cosφsinθsinφsinθcosθ]T。因此，用量子位在Bloch球面上的坐标对染色体进行编码，即

(8)

在式(8)的编码方式中，φij=2π×rand；θij=π×rand；rand为(0,1)之间的随机数；i=1,2,…，sizepop，j=1,2,…,n，sizepop表示种群规模，n表示量子位数(即：待优化的变量个数)。BQGA中，每条量子染色体包含三条并列基因链， 即量子位的xyz坐标， 而每条基因链表示待优化变量的一组近似解；

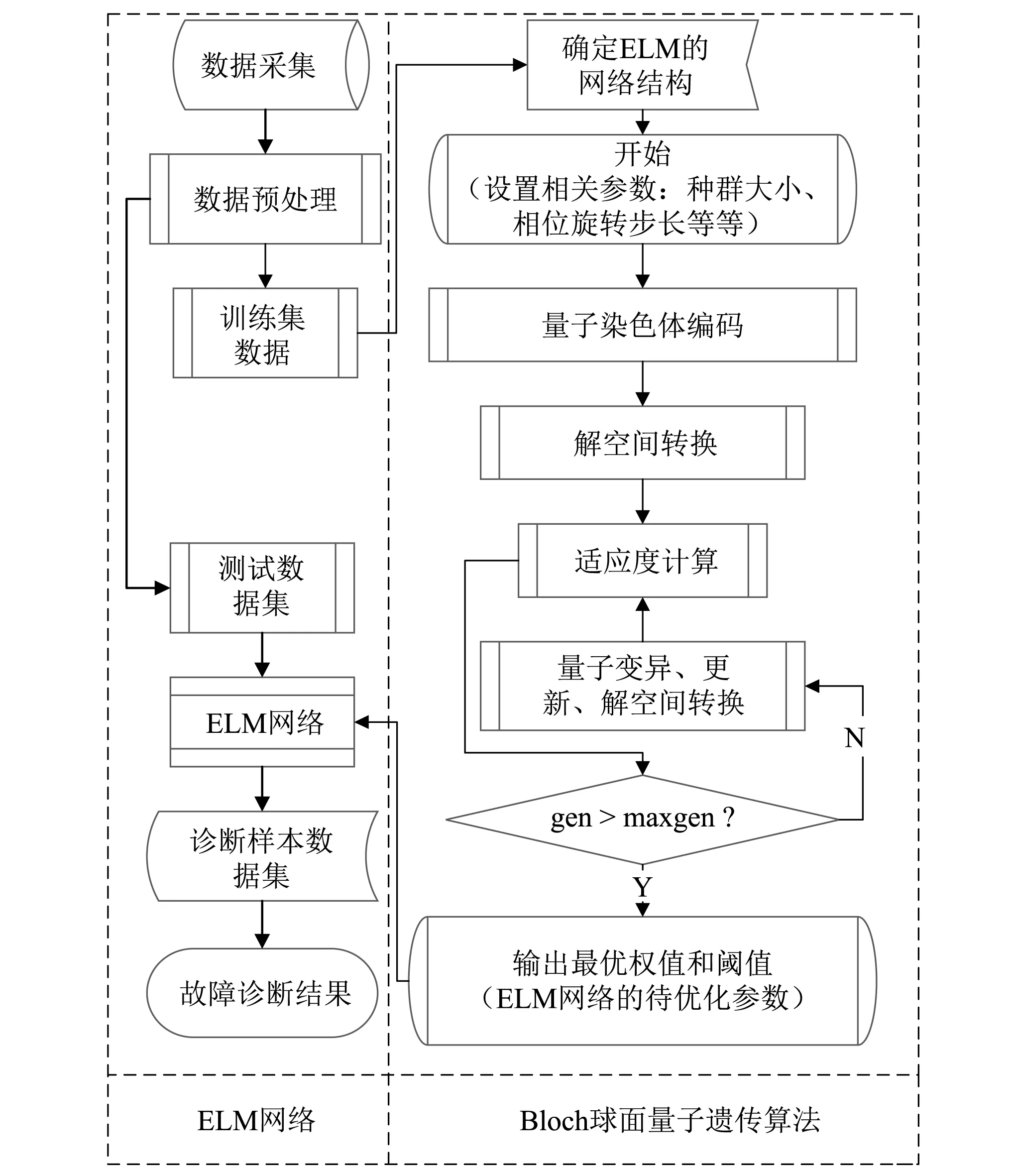
图1 BQGA-ELM算法流程图Fig.1 Flowchart of BQGA-ELM algorithm

步骤3将三组近似解进行解空间转换，即将近似解转换到目标函数的解空间；

步骤4根据式(9)的适应度函数，计算近似解的适应值。找出当前最优适应值与对应的当前最优染色体，同时将当前最优解转存为全局最优解；

①见“UN should play a more effective role”.Beijing Review,1 November 1982:11-12．

(9)

式中：n为校验集样本数量；yi为网络期望输出；oi为真实输出。

步骤5利用量子旋转门U，更新量子染色体，得到新的量子染色体，即式(10)

(10)

式中：Δφ和Δθ为相位旋转步长。

步骤6对旋转更新后的新染色体进行解空间转换，并计算新染色的适应度值，保存当前最优解与对应的染色体；

步骤7比较当前最优解和全局最优解。如果当前最优解优于全局最优解，则全局最优解被替换；否则继续；

步骤8判断是否满足终止条件。若是，则输出最优解；若否，则继续循环执行步骤5～步骤7。

2.2 算法仿真校验

为了验证BQGA在ELM网络优化中的可行性，选取UCI标准数据库中的Wine和Abolone两个标准数据集作为实验数据，仿真数据集的相关属性及数据集分配如表1所示。对比研究Bloch球面量子遗传算法优化ELM网络(BQGA-ELM)、量子遗传算法优化ELM网络(QGA-ELM)、粒子群算法优化ELM网络(PSO-ELM)、经典遗传算法优化ELM网络(GA-ELM)以及未被优化ELM网络六种方法之间的性能，此六种方法文中简称为诊断模型。ELM网络的四种激活函数(Sigmoid()、Hardlim()、Sin()、RBF())均被考虑其中，计算结果中主要呈现测试集诊断准确率、均方根误差、神经元数量以及计算耗时。

比较研究采用的计算机配置为:AMDA8-5500B APU with Radeon HD Graphics四核处理，金士顿DDR3L 4 G 800 MHz内存，文中所有算法均在MATLAB2014a上运行。

对比算法的参数设置说明：遗传算法共有参数设置如下，种群大小为20，迭代步数100，种群范围为[-0.5 0.5]；传统遗传算法交叉概率为0.6，变异概率为0.05；经典粒子群算法中，种群粒子数为20，迭代步数为100，粒子最大速度为0.1，最小速度为-0.1，粒子范围为[-0.5 0.5]；量子遗传算法中的变异概率为0.05；相位旋转角均为：0.01π；ELM网络中神经元数量设置见表。计算结果统计如表2和表3所示。

表1 仿真数据样本集信息

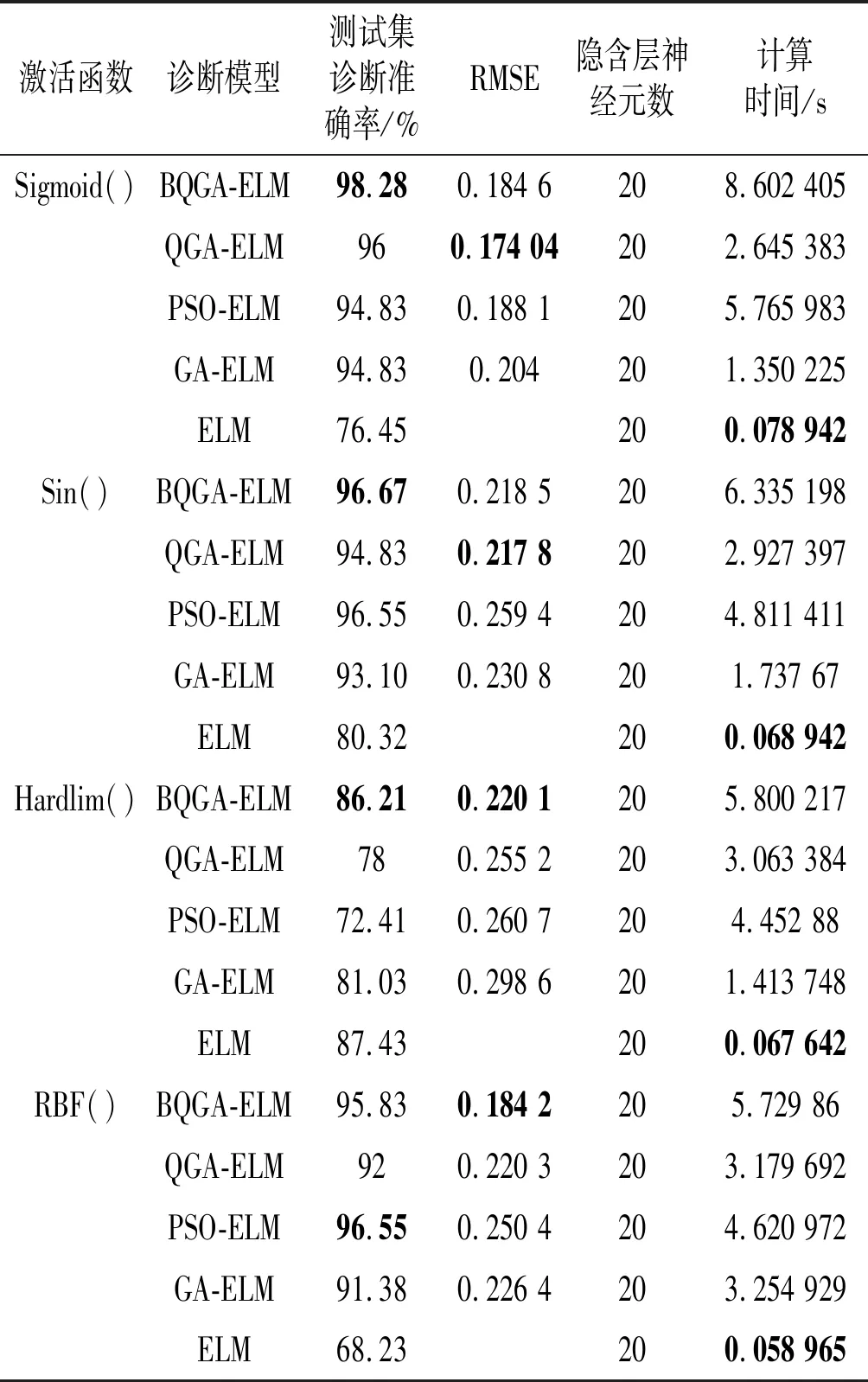
表2 样本集Wine的诊断结果

表3 样本集Abolone的诊断结果

表2和表3呈现不同方法优化ELM网络后的计算结果，计算结果均为30次分类实验后的平均值，计算得到的最优结果在表2和表3中已用黑体加粗进行标记。在不同激活函数下，诊断效果差异较为明显，因此使用ELM网络时，应适当选择激活函数。从表2和表3中的加粗黑体可以发现，BQGA-ELM模型的诊断效果最好，PSO-ELM模型其次，ELM网络最差；这一结果表明BQGA在空间寻优的能力由于其它方法，但随着其搜索维度的增加，计算量增大，其计算时间也相应增加；同时也凸显出优化的ELM克服了ELM网络中的部分缺陷。需要注意的是，ELM网络隐含层神经元数对分类结果有影响，由于仿真测试小节并非本文的重点，所以此处并未对神经元数量进行分析，只是为了验证文中诊断模型的可行性。

3 滚动轴承故障数据采集实验

3.1 轴承故障实验简介

由于航空发动机轴承故障数据采集难度较大、成本较高，因此故障数据通过实验模拟的方式获得。滚动轴承故障诊断实验装置如图2所示。

图2 滚动轴承实验装置Fig.2 The test rig of the rolling element bearing

其中，实验中所用设备包括：307型滚动轴承、加速传感器、光电传感器、电荷、信号调理机、计算机等。轴承座可以拆卸， 便于更换不同故障类型的轴承。联轴器上贴有反光纸作为相位起始标志，光电传感器提供转速和键相信号；置于故障轴承轴向、径向垂直和径向水平方向的加速度传感器测得轴承振动信号；最后再经过电荷放大器送至设备CAMD-6100型信号调理器处理。

实验中转子转速为988 r/min，每周期传感器采样1 024个点，每次实验采集16个周期。307型滚动轴承几何参数如表4所示；实验故障类型为：正常、内环故障、外环故障、滚珠故障，故障类型尺寸数据如表5所示，故障类型加工图如图3～图5所示。

表4 307型滚动轴承的几何参数

表5 滚动轴承模拟故障类型

图3 滚动轴承内环单处划痕故障示意图Fig.3 The single scratch fault on the inner ring

图4 滚动轴承外环单处划痕故障示意图Fig.4 The single scratch fault on the outer ring

图5 滚动轴承滚珠单点点蚀故障示意图Fig.5 The single erosion fault on a ball

3.2 轴承振动信号处理方式

在时域分析法中，特征参量峰值、峭度系数均为无量纲参数，且时域分析法处理过程不会使信号发生畸变或损失，采用最原始信息资料进行轴承故障诊断。首先，对采集到的轴承故障振动信号先进行时域分析；再利用SPSS软件进行因子分析，根据碎石图特征值递减情形选择累积方差贡献率达到90%的因子，即：峰值、均值、均方根、方差、偏度、峭度；最后将这6个因子作为307型滚动轴承故障诊断的输入特征量。

3.3 滚动轴承故障数据集样本分配

将得到的数据集样本分为：训练集样本、校验集样本、测试集样本三部分，三部分数据随机选择，彼此互不重复。文中所用样本分配如下：训练集样本容量为200个，校验集样本容量为100个，测试集样本容量为100个。

4 滚动轴承故障诊断实例

4.1 数据标准化

为了避免故障特征量之间的数量级差异给诊断结果带影响，因此按如式(11)进行归一化处理

(11)

式中：xmax，xmin和xmean为某特征参量的最大值、最小值和平均值；xi是某特征参量的第i个值；x是归一化后的值。

4.2 BQGA-ELM模型的输出形式

极限学习机网络采用三层结构，即：输入层、隐含层和输出层。输入层神经元个数为：6个；隐含层神经元个数设置将影响到网络诊断准确率，下小节将对隐含层神经元数量和激活函数进行分析；输出层神经元个数设置为1，对于输出神经元输出结果的处理方式如表6所示。

表6 输出结果的处理方式

4.3 隐含层神经元数量和激活函数的选择

利用滚动轴承故障样本数据，对几种诊断模型进行分析，选择合适的激活函数和神经元数量。在不同激活函数的前提条件下，分析神经元数量与测试集诊断准确率之间的关系，从而选择合适的激活函数与神经元数量。其计算结果如图6所示。

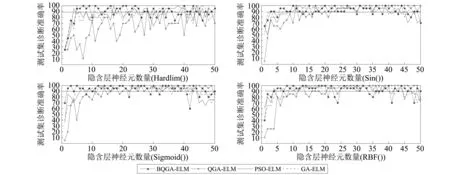
图6 隐含层神经元数量和激活函数的选择Fig.6 Choose of activation function and number of hidden neurons

从图6中可以看出，几种诊断模型在Hardlim()和RBF()函数下，测试集诊断准确率波动较为明显；而在Sigmoid()和Sin()函数下，变化较为平缓，尤其在神经元数量处于[10,40]范围内时，效果较好。直观看来，诊断模型选择Sigmoid()和Sin()函数时，对几种算法而言效果均较好，且可比性较强；为了更加具有说服性，在每种激活函数下，统计各诊断模型测试准确率大于等于90%时出现的次数，并定义为频数，根据诊断模型频数的变化大小选择激活函数。统计结果可视化为图7所示。

从图7中可以看出，当激活函数为Sigmoid()，Sin()和RBF()时，几种诊断模型的频率均相对较高。但仔细观察发发现：在RBF()和Sin()函数下，几种诊断模型之间的最大差异分别可达到15%和20%左右，不利于对比评估；而在Sigmoid()函数下，几种诊断模型之间的差异最大可达到10%，相对较小。经过分析，选择差异较小Sigmoid()函数作为几种诊断模型的激活函数。因此，文中诊断模型的激活函数为Sigmoid()，神经元数量取值范围为[10,40]。

图7 根据频数选择激活函数Fig.7 Choose of activation function according frequency

4.4 诊断结果评价标准

采用30次诊断后的平均值为文中评定的标准，平均诊断准确率按式(12)计算

(12)

式中：Accuracymean为平均准确率；T为重复诊断次数；y(t)为第t次诊断时，样本诊断正确的个数；m为需要诊断的总样本数量。

5 滚动轴承故障诊断结果分析

在本章节中，将从平均诊断准确率、误差收敛情况以及诊断耗时三方面分析BQGA-ELM在滚动轴承故障诊断中的有效性。

5.1 平均诊断准确率

将在滚动轴承故障实验章节中得到的四种轴承故障特征参量样本，经过数据归一化后，按照样本分配方式进行随机且不重复的分配。将分配好的训练集样本输入诊断模型中进行训练，用校验集样本对模型训练效果进行校验，选取最优权值阈值优化ELM网络，并对测试集样本进行诊断，其诊断结果如表7所示(最优结果已用黑体加粗标记而出)。

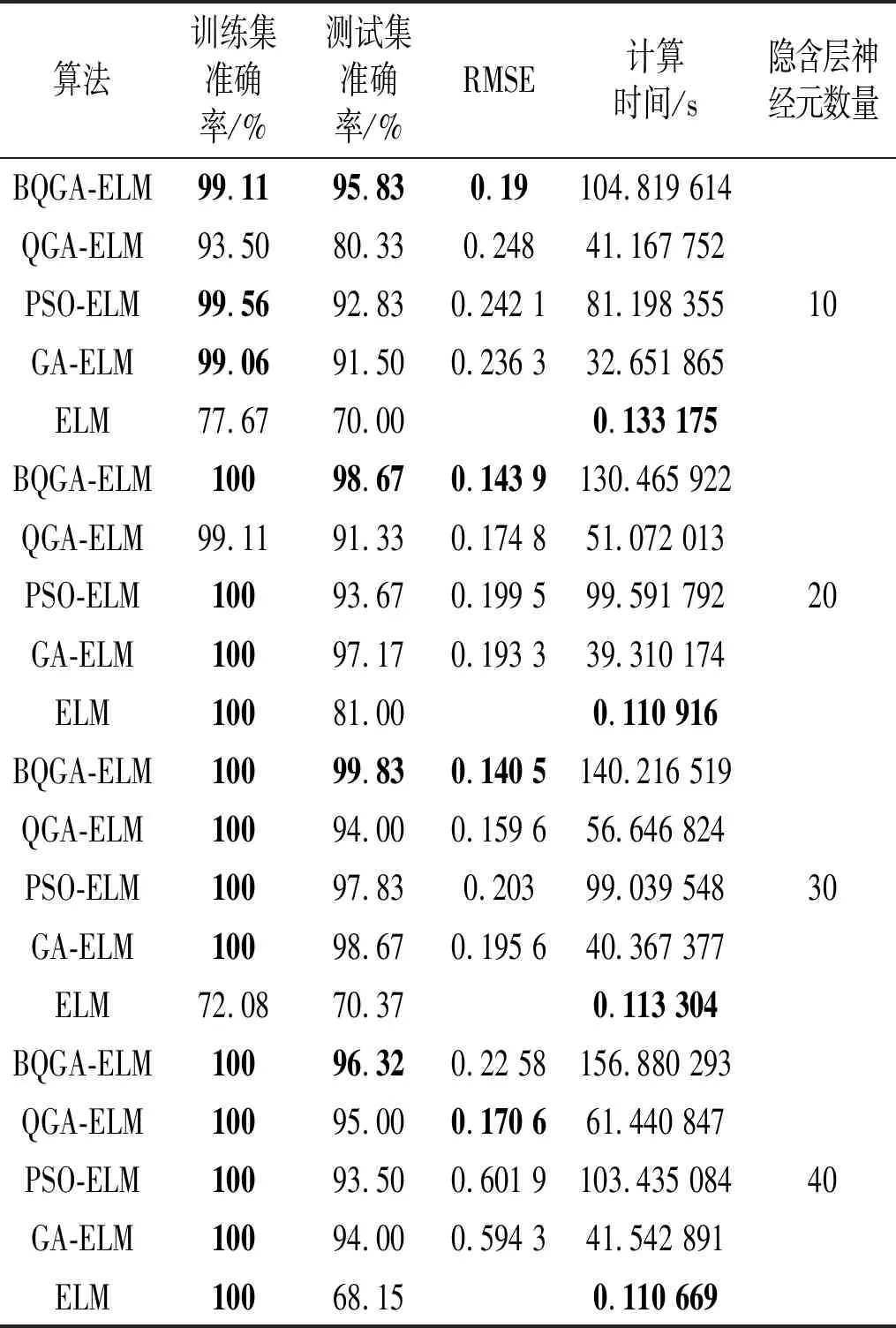
表7 不同诊断模型的平均诊断准确率

从表7的诊断结果可以看出，BQGA-ELM诊断模型对测试集样本的平均诊断确率最高，校验集RMSE收敛值也最低。当神经元数量为20，30和40时，诊断模型对训练集样本的诊断率均能达到最好，说明此时网络对训练集样本利用充分，得到的训练效果也最好；而这一结论也在测试集样本中得到证明，除了ELM诊断模型之外，其它诊断模型对测试集样本的平均诊断准确率均能达到90%以上。由于优化算法在寻优的过程，需要进行反复计算，因此被优化的ELM网络诊断模型的诊断时间(=训练时间+测试时间)均有所增加。但在实际故障诊断中，诊断模型先对故障样本进行大量训练，用训练好的模型再去对故障进行诊断，因此会减少大量的计算时间(详见“5.3”节)。因此，经过分析，BQGA-ELM相比于其它诊断模型，更加适用于滚动轴承故障诊断中。

5.2 误差收敛

为进一步验证BQGA-ELM诊断模型性能优于其它诊断模型，因此本小节从误差收敛角度进行分析。当神经元数量为30时，几种诊断模型误差收敛如图8所示。从图8中可以发现，PSO-ELM和GA-ELM最先收敛，但收敛值却较差，这表明GA和PSO可能陷入了局部极优，导致寻优终止；而BQGA-ELM和QGA-ELM能够收敛到更小值，这得益于量子计算的并行性与搜索维度的增加。从误差收敛角度分析，BQGA-ELM诊断模型的性能优于其它三者诊断模型。

图8 不同诊断模型的平均收敛误差Fig.8 Average convergence error of different diagnostic models

5.3 诊断耗时

从表7中可以发现，除了ELM诊断模型，其它诊断模型计算时间均有所增加。表7中所给出的计算时间为训练时间和测试时间之和，而实际故障诊断中，诊断模型都是在诊断训练完成之后再对故障进行诊断。因此，在本小节中，分开统计训练时间和诊断时间于表8中，并进行分析。从表8中可以看出，诊断模型训练时间较长，但测试时间均较短。其中，由于BQGA相比于QGA增加了搜索维度，从而增加了量子染色体基因链的数量，这便导致计算量增加，尤其再重复运算过程中，时间累积效果更为明显；但其诊断时间可以接受。ELM诊断模型训练时间和诊断时间均较短，但其平均诊断准确率却较低。同时，需要注意的是，诊断模型的训练和诊断时间与计算机硬件设施存在一定的关系。因此，经过分析，BQGA-ELM诊断模型相比文中其它诊断模型更适宜于滚动轴承故障诊断。

表8 平均计算时间

6 结 论

提出一种基于Bloch球面量子遗传算法优化ELM网络的诊断方法，利用BQGA并行、多维度的全局搜索能力，依据校验集样本的RMSE收敛情况，自适应的选择ELM网络的输入权值和阈值，并将其应用于滚动轴承故障诊断中。通过仿真实验，将BQGA-ELM，QGA-ELM，PSO-ELM，GA-ELM和ELM进行数据分类实验对比，利用UCI标准数据中的两组数据作为被测数据；仿真结果表明，BQGA-ELM在数据分类实验中的有效性。

利用时域分析法提取实验室采集到的轴承故障诊断振动信号的特征参量，并将其作为BQGA-ELM的输入参数，进行滚动轴承故障诊断。诊断结果表明：BQGA-ELM在平均诊断准确率、误差收敛性能以及故障诊断时间中均占据优势。