动静荷载分离思路下高铁基床累积变形计算方法

商拥辉,徐林荣,陈钊锋

(1.黄淮学院建筑工程学院,河南驻马店 463000； 2.中南大学土木工程学院,长沙 410075； 3.高速铁路建造技术国家工程实验室,长沙 410075)

引言

实现长期循环荷载作用下基床结构累积变形有效控制是建造高铁技术难点之一[1-2]，各国对发展高铁非常重视，相应制定了各自控制标准。例如：日本规定路基面动变形小于2.5 mm[3]；德国荷载引起沉降限值为5 mm[4]；中国高铁动载引起路基基床变形以≤3.5 mm为控制条件[5]。标准无法反映累积变形随时间与空间变化规律。Seed[6]、Barksdale[7]、Gidel[8]等分别对黏性土累积变形进行了研究，并建立了简化经验公式；王建华[9]、蔡英[10]、陈云敏[11]、钟辉虹[12]及黄茂松等[13]提出了能够兼顾考虑加载次数、频率和波形、应力水平及超固结比等影响因素的软土累积变形经验公式。高铁路基核心基床采用A、B组填料，承担动应力幅值与加载频率与一般干线有别，邓国栋[14]、梅慧浩[15]等借助TAJ-2000大型动三轴试验仪，提出了能够考虑频率、围压及应力路径等因素的粗颗粒填料的累积变形经验模型。

经验公式建立在诸多简化之上，且存在物理指标定义不明确、参数选取困难等问题。随着“列车-轨道-基床”力学模型不断完善，部分学者借助数值模拟对高铁基床累积变形规律进行了探索。孔祥辉等[16]总结了动应力沿路基深度逐渐减小，基床表层内衰减可达45%；边学成等[17]总结了列车动载作用100万次基床累积变形约2.3 mm；叶阳升等[18]总结了列车动载作用400万次基床累积变形1.4～2.8 mm。数值模型能够建立实际列车-基床振动机制，可以实现多种荷载工况路基变形分析，相比经验公式而言，具有较大进步，不足之处在于数值模型多假设，材料均值、材料本构模型及计算参数与实际工况仍存在差异。

就目前而言，测试途径仍是获取基床累积变形最可靠方法。屈畅姿[19]、王启云[20]等借助1∶1单线无砟轨道路基模型，总结基床累积变形随加载次数呈先快速后趋于增长趋势，稳定时累积变形约2 mm。即便足尺模型，仍存在设备精度差异与地基模拟局限等问题。郑键斌[21]结合现场激振试验，总结了京沪高铁桩板式低路堤路面沉降主要发生在加载前120万次，200万次结束时达到0.39 mm；王亮亮[22]总结了云桂高铁石灰膨胀土路基面和地基面，激振200万次时累积沉降分别为2.8 mm和0.3 mm。原位激振试验有效避免了室内模型试验地基无限域引起的测试精度问题，缺点在于单轴载作用难以考虑转向架之间动力叠加问题，而效果最好的现场行车试验所需费用昂贵，推广研究范围有限。

高铁在建造与运营过程中，对路基沉降积累大量测试数据，如能将其利用达到分析路基累积变形的目的则意义重大。基于此，笔者在充分分析运营期路基沉降组成特点上，基于分离动、静荷载引起沉降的新思路，提出一种结合实测数据推算与估算基床累积变形的新方法，并应用到沪宁城际铁路分析中，为探索高铁路基基床累积变形提供一种新的借鉴途径。

1 推算与估算新思路概述

结合路基运营期沉降组成特点，基于分离运营期动、静荷载引起沉降的思路，提出基床累积变形推算及估算新方法，具体表述如下。

(1)推算方法。将运营期沉降数据推算工后沉降u1与建设期沉降数据推算工后沉降u2差值近似作为动载引起变形S1。

S1=u1-u2

(1)

(2)估算方法。将运营期沉降δ1与对应静载计算固结沉降δ2差值近似作为动载引起变形S2。

S2=δ1-δ2

(2)

由式(1)和式(2)可知，推算与估算涉及计算内容：①由运营期沉降数据推算工后沉降；②由建设期沉降数据推算工后沉降；③静载条件复合地基固结沉降计算。其中，①和②工作内容可以归结于对实测数据进行规律性顺延推测。目前，结合实测数据进行路基沉降推测方法较多，文中采用课题组致力完善的动态神经网络法[23]，固结度计算借鉴课题组最新成果相关内容[24]。

2 推算/估算实例分析

2.1 计算断面选取

沪宁城际铁路正线全长300.209 km，于2010年7月2日正式运营。全线位于江苏省境内，软土路基长62.333 km，路堤填土高度2～10 m，堆载预压最短时间3个月(规范要求>6个月)，设计速度300 km/h以上。自运营以来，对全线路基共6974个测点(CPⅢ点、底座板、轨道板和基准轨)进行多期次沉降监测，线路运行状态良好。计算选取断面参数详见表1～表4。

表1 断面土层物理力学参数

表2 CFG桩参数

表3 钢筋混凝土筏板参数

表4 垫层与路堤填土参数

2.2 推算与估算结果分析

图1为4个断面推算累积变形曲线随时间发展曲线。

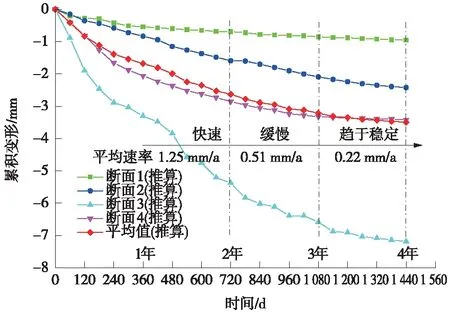
图1 累积变形推算结果

由图1可知：不同断面累积变形曲线离散度较大，这与各断面路基填筑高度、软土地基参数及CFG桩长相关，其中断面3累积变形发展速率与量值相对较大，主要考虑路基填筑高度(5.36 m)较高，相应竖向荷载较大，软土层易受上部附加应力(静+动荷载)产生变形，侧面也说明累积变形与地基前期处治存在关联；不同断面推算累积变形整体发展趋势吻合，基本呈现“快速-缓慢-稳定”3阶段特征，说明推算方法具有一定的合理性，可以反映累积变形随时间变化的发展特点；采用平均值分析各断面累积变形-时间关系可知：运营前2年累积变形随时间发展迅速，速率1.25 mm/a，随后趋于缓慢发展；运营3年后，累积变形随时间增幅相对较小，速率仅为0.22 mm/a；稳定时断面1、断面2、断面3和断面4推算累积变形值依次为0.95，2.42，7.19 mm和3.42 mm，平均值约为3.49 mm。

图2为4个断面估算累积变形曲线随时间发展曲线。由图2可知：与4个断面的推算结果离散性略大不同，不同断面估算曲线吻合度相对更高；运营期前2.6年累积变形快速发展，平均速率约为0.67 mm/a，随后2.6～3年累积变形速率降为0.38 mm/a；运营3年后累积变形趋于稳定，速率约为0.20 mm/a(该阶段速率与推算结果速率0.22 mm/a基本相等)；最终稳定时断面1、断面2、断面3和断面4估算累积变形值依次为1.92，2.16，2.42 mm和2.21 mm，平均值约为2.18 mm。

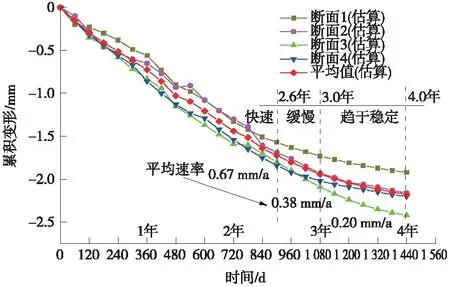
图2 累积变形估算结果

考虑到推算结果的离散性特性，仅将推算平均值与估算平均值进行对比分析，探索两者之间的差异。由图3可知：推算与估算平均值曲线发展规律吻合，验证了两种不同方法获取累积变形结果具有一定可信性；然而推算结果整体大于估算结果，差值约为1.31 mm，侧面说明两种方法存在一定误差。为此，需要进一步借助数值模型对其合理性进行验证。

图3 推算与估算结果对比

3 推算与估算结果可靠性论证

3.1 数值模型建立

结合沪宁城际高速铁路工况，建立列车-轨道-路基空间动力系统数值模型，模型建立过程参考文献[25]。地基模型X、Y、Z方向尺寸为60 m×30 m×200 m。为近似模拟地基无限域边界条件，模型地基部件Y方向限制法向位移，底边采用固定约束。模型除基床上部轨道结构、复合地基垫层及CFG桩采用BEAM单元外，其他采用部件C3D8R实体单元，建立模型详见图4，地表以上路基部件计算参数见表5，地基与CFG桩基等部件参数详见表1～表4。

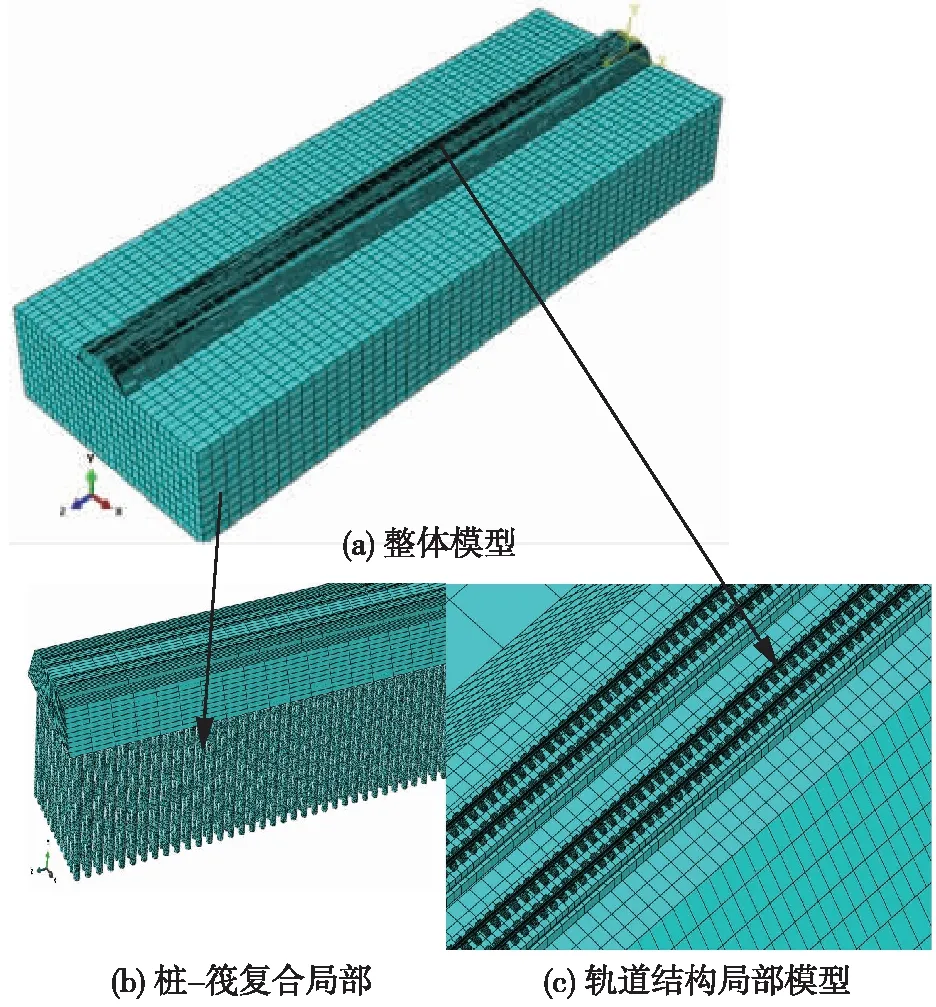
图4 数值模型

为便于计算，将列车荷载简化为能考虑速度、轮重、线路平顺性等因素的函数表达式

F(t)=P0+Mα(2πv/L)2sinωt

(3)

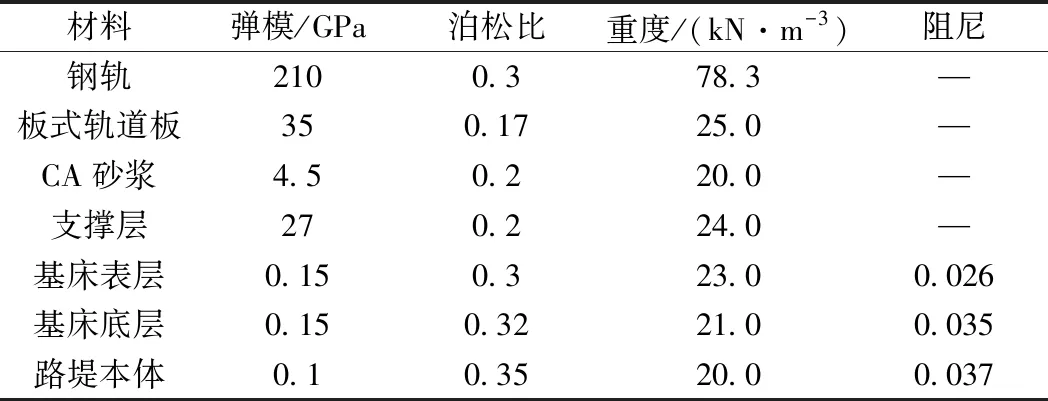
表5 计算参数

式中，P0为车轮静载；M为簧下质量；α为反映路况几何不平顺矢高(取3.5 mm)；v为列车速度；L为几何不平顺曲线波长(取10 m)。按照公式(3)可输出列车激励力时程曲线(举例图5)。

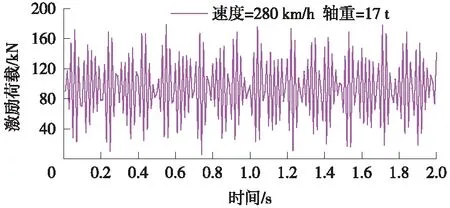
图5 计算中施加的动力波形

3.2 数值模型合理性分析

数值模型建立在诸多简化基础之上，需要对其合理性进行验证。文献[26]结合室内模型试验，对高铁路基振动响应进行了测试，获取了不同深度动应力，借助本文建立数值模型对该文献中试验工程进行模拟，通过对比两者之间的差异论证本文数值模型的合理性。

由表6可知：采用本文数值模型分析结果与室内模型测试结果基本吻合，不同深度位置两者动应力误差范围0～0.73 kPa；数值模型计算结果略高于模型测试结果，说明本文模型计算结果相对保守，偏安全。可见，本文数值模型建立方式与计算参数选取合理，计算的精度可以满足后续分析需求。

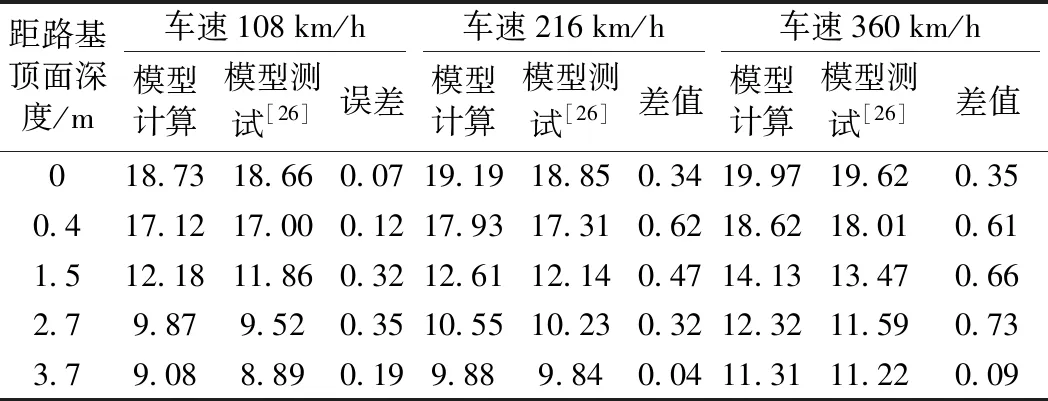
表6 数值结果与模型测试动应力对比 kPa

3.3 数值模拟与推算与估算结果对比分析

结合上述数值模型，对断面1～断面4累积变形进行计算。由图6可知：不同断面累积变形随时间增加均呈现快速、缓慢和稳定3阶段变化特征；累积变形在运营开始后前1.5年内发展相对较快，速率约0.11 mm/月；运营开始后1.5年～3年累积变形进入缓慢发展阶段，变形速率为0.03 mm/月。稳定时，断面1～断面4累积变形值基本范围2.38～2.65 mm。

图6 累积变形数值计算结果

由数值结果可知，4个断面获取累积变形曲线较为吻合，与估算结果类似。因此，可通过推算/估算与数值计算平均值对比分析不同方法获取累积变形差异，对比曲线详见图7。

图7 累积变形平均值对比

由图7可知：不同方法获取累积变形曲线随时间均呈快速、缓慢和稳定3阶段特征，且在运营前3年期趋于稳定；推算法、模型计算及估算法3种不同途径获取路基累积变形平均值依次为3.5、2.2 mm和2.5 mm；快速发展阶段，数值模拟与推算曲线较为吻合，而累积变形进入缓慢阶段后逐渐与估算结果更为接近，两者差值约为0.6 mm。考虑推算结果的离散性，估算结果与数值结果吻合，验证了本文所提估算方法具有较高的可靠性。同时，推算方法作为一种新的思路，后期仍需进一步对其推算过程进行完善。

4 结论

依托工程实例，提出高速铁路基床累积变形特性推算与估算新方法，主要结论如下。

(1)推算、估算及数值计算基床累积变形曲线随时间发展均呈快速、缓慢和稳定3阶段特征，且累积变形在运营前3年基本稳定，3种方法获取累积变形平均值为3.5，2.2 mm和2.5 mm。

(2)推算方法引入动态神经网络，估算方法静载沉降计算考虑了桩-土变形协调及其接触面的荷载传递特性，两种方法存在差异，但获取累积变形规律大致一致。相比推算法4个断面结果离散性较大，估算法一致性较好，且与数值模型计算结果一致性较为接近。

(3)推算及估算主要借助现场测试沉降数据及路基力学参数进行累积变形分析，在保证分析结果满足精度要求的同时，相比室内路基模型试验和现场激振试验，具有更高经济、实用和科研价值，值得推广应用。