基于实证数学规划模型的农业水价政策效应模拟
谭 倩,王淑萍,张田媛
基于实证数学规划模型的农业水价政策效应模拟
谭 倩,王淑萍,张田媛
(中国农业大学水利与土木工程学院,北京 100083)
水价政策的合理制定对水资源高效利用意义重大。水价政策的决策过程往往主观性过强,缺乏水价政策效应的量化研究方法。针对多水源多灌溉方式下的农业灌区,基于实证数学规划方法构建农业水价政策效应模拟方法。将建立的方法应用于甘肃省民勤县进行实证研究,分别模拟了3种水价政策下用水效益、灌溉用水量、种植占地和节水灌溉工程面积等对水价上涨的响应机制,分析了不同政策下的水价上涨阈值和不同水价水平下的适宜政策。结果表明:在单一水价和两部制水价政策下,民勤县农业水价宜处于0.24~2.10元/m3之间;在差别水价政策下,水价宜处于0.24~1.50元/m3之间;当计量部分水价低于2.10元/m3或高于6元/m3时,差别水价政策的综合效益最高;当计量部分水价在2.10~6元/m3之间时,单一水价政策最为理想;实行差别水价政策且计量部分水价为1.50元/m3时取得的单方水效益最高。该文证实了民勤县目前实行的差别水价政策是适宜的,水价的稳步上涨不会降低用水的综合效益,但应在水价上调的同时考虑当地实际情况,且注意加大对节水灌溉工程的投入和建立配套的农户收入补贴政策。该文建立的农业水价政策效应模拟方法具有较广泛的适用性。
农业;水;模型;实证数学规划;水价政策;用水效益
0 引 言
水资源是最珍稀的自然资源之一,关系着人类的生存与发展[1-2]。水价是水资源管理的重要手段。一方面,价格杠杆有望缓解农业用水紧张的问题[3-4]。另一方面,水价政策的制定与农户收入、农业生产、能源消耗和粮食安全等其他经济、社会与环境要素密切相关[5-6]。水价过低会导致农户节水积极性下降、灌溉用水量增高、水资源利用效率降低等诸多负面问题;水价过高会影响正常的农业生产活动,降低农户的收入与生活质量,不利于农业的可持续发展。因此,在充分理解农业水价政策效应的基础上合理制定水资源价格政策,具有重要的科学研究价值和应用前景。
长期以来,中国实行无偿或低价农业水价政策,导致水资源被过度开发和大量浪费[7]。当前,国家已开始在部分地区推行农业水价综合改革,以期得到更合理的农业水价政策实施方案。然而,农业灌溉系统包含资源、技术、经济和社会等诸多互相关联的子系统和驱动因素,并涉及多种水源、灌溉技术与作物类型,其水价改革对农业行为以及经济收益等带来的影响错综复杂[8-9]。现有研究与实践工作对水价政策的制订多采取经验与类比方法,主观性过强,且鲜有针对多水源、多灌溉方式类农业灌区的水价政策进行效应模拟、预测与比较[10-11]。
近年来,国内外已出现一些研究水价政策效应的量化方法。其中,计量经济学方法难以预测新政策的实施效果、无法真正反映用户面对新政策的决策机制和过程,且需要大量的数据[12-13]。一般可计算均衡模型对样本数量要求极高且方程参数难以准确确定[14-15]。除这2种常用的经济学模型外,国外也有学者采用数学规划方法来模拟政策效应[16],该方法通过添加约束来限定决策变量的变动范围,虽能保证模型计算结果与实际观测值相近,但降低了模型的灵活性。实证数学规划(positive mathematical programming,PMP)是一种能够自校准的政策效应模拟方法,它对样本数量要求低,可反映决策机制和过程,能将模型的输出结果精确校准至实际观测值并在其基础上预测新政策的实施效果[17-18]。Heckelei等[19]认为PMP模型弥补了经济学模型和传统数学规划模型的不足,在这2类模型间起着桥梁作用。
目前PMP方法在农业经济、环境、资源政策分析与评估中有了较为广泛的应用[20]。Iglesias等[21]首次将PMP方法应用在水价政策效应的研究中,模拟了计量水价政策下,灌溉用水、农户收入、肥料使用量等指标随水价上升的变化情况。随后,Gallego-Ayala等[22-26]在Iglesias的基础上,分别利用 PMP方法从不同角度对水价政策效应开展了进一步的研究。然而,以往基于PMP的水价政策效应研究尚存在一些不足:1)在模型结构上仅涵盖单一水源,且未考虑粮食、能源供需方面的限制,对采用多水源、多灌溉方式的农业灌区来说并不适用;2)对水价政策效应规律的探讨不够深入。在对水价政策进行模拟时,尽管部分研究得出了某一政策下各效应指标随水价上升的变化趋势,但未能进一步分析响应规律并提出水价阈值。在进行不同水价政策间的横向比较时,现有研究仅主观选择零星的水价政策方案或水平,且往往局限于农户收入、灌溉用水量等少数几个效应指标,未能在多个效应指标下对一系列水价政策方案进行量化比较后得出不同水价水平所对应的适用政策(即政策适用范围)。
基于以上背景,本研究针对多水源多灌溉方式下的灌区,构建基于PMP的农业水价政策效应模拟方法,在灌区农业水价政策制定前,对构想新政策的实施效果进行预测。以农业水价综合改革试点区甘肃省民勤县为例,对不同农业水价政策的实施效果进行模拟和比较,进一步得出不同政策制度下的水价上涨阈值和不同水价水平下的适宜政策。本研究旨在科学地揭示水价上涨的政策效应,以系统最优化为目标,从理论角度探索不同政策下的水价上涨阈值和不同水价水平下的适宜政策,并以此来减少水价政策实施可能造成的经济、资源风险,而非囿于提出具体的水价建议值。这是由于,水价的制定从来都是自然、经济和社会、政治、历史等多维因素共同作用的结果。在厘清水价上涨对各效应指标的客观影响机制之后,还需征求多方意见,并综合考虑当地现有水价、农民承受能力、政府财政补贴等多种因素来确定具体的实施水价。
1 PMP方法建立
1.1 PMP核心思想
PMP模型研究始于20世纪90年代初,是在Heady等早期研究基础上开展的[27-29]。最常用PMP模型由Richard教授于1995 年正式提出,其核心思想在于,假定观测到的农户生产行为是最优化的结果,认为农户生产决策不但取决于可观测的成本收益,还会受到不可观测因素的影响,如农民知识水平、土壤养分状况等,并通过基准期的校准将这些不可观测因素体现在模型中,使得模型输出结果与实际观测值一致[17,30]。本研究针对多水源多灌溉方式下的灌区,构建基于PMP的农业水价政策效应模拟方法。在现行水价政策下,利用基准期实际观测数据和PMP方法对农业水价线性规划模型进行校准,计算模型中的未知参数。将未知参数代入模型,先验证模型在基准期的最优解与实际种植面积保持一致,再用于后续不同水价政策的效应模拟。
1.2 PMP模型构建及求解
1.2.1 建立并求解灌区农业水价线性规划模型得到校正约束对应的对偶值
以农户纯收入最大为目标,以不同地区不同水源不同作物不同灌溉方式的种植面积为决策变量,构建灌区农业水价线性规划模型,其中,约束式(3)为保证决策变量实际观察值和计算结果一致的校正约束,其他约束均为资源约束,具体模型如下所示。
目标函数:


约束条件:
1)决策变量实际观察值校正约束

2)最大最小总种植面积的约束
耕作作物的总面积应小于可用耕地的总面积,大于保留耕种的最小面积。
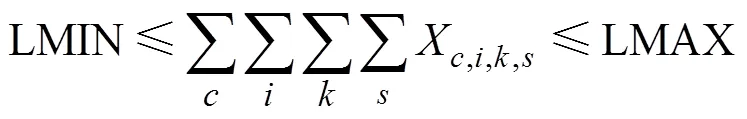
式中LMIN为当地保留耕种的最小种植面积,hm2;LMAX为当地可用耕地的总面积,hm2。
3)地表水可用水量约束
用于各作物灌溉的地表水之和,不高于农业灌溉的地表水可用总量。

式中SW为地表水总可用水量,m3;为地表水总可用量中可用于农业灌溉的比例,%。
4)地下水可用水量约束
用于各种作物灌溉的地下水之和,不高于农业灌溉的地下水可用总量。

式中GW为地下水总的可用水量,m3;为地下水总可用量中可用于农业灌溉的比例,%。
5)可用电量约束
抽取地下水和滴灌节水技术的用电总量,不高于农业灌溉的最大可用电量。
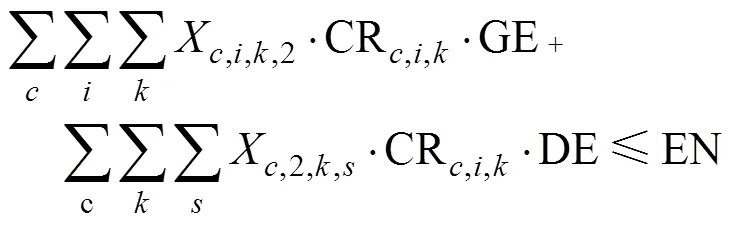
式中X,i,k,2为区域内以地下水为水源的作物在灌溉方式下的种植面积,hm2;GE为抽取地下水灌溉的单位耗电量,kWh/m3;X,2,k,l为区域内以水源的作物在滴灌方式下的种植面积,hm2;DE为滴灌技术灌溉的单位耗电量,kWh/m3;EN为农业灌溉的最大可利用电量,kW·h。
6)粮食需求约束
为确保研究区各种作物的自给自足,引入了粮食安全约束,它根据总人口和人均作物需求确定。

式中D为人均作物需求,每人每年粮食占有量不得少于400 kg,其他作物的最小需求量由《中国居民膳食指南》[31]查得,kg/(人·a);TP为研究区人口总量,人。
7)人均最小耕地面积约束
为了维持人口和农民的收入,确定最小耕地面积约束。

式中MAL为人均最小耕地面积,hm2/人。
8)决策变量非负约束
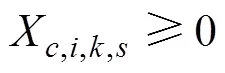
通过求解上述线性模型,可得到对应校正约束的对偶值,该值间接提供了与成本相关的信息。
1.2.2 利用校正约束对应的对偶值对灌区农业水价线性规划模型进行校准
根据边际收益递减的经济学假设,将成本函数设为一元二次[17]形式:
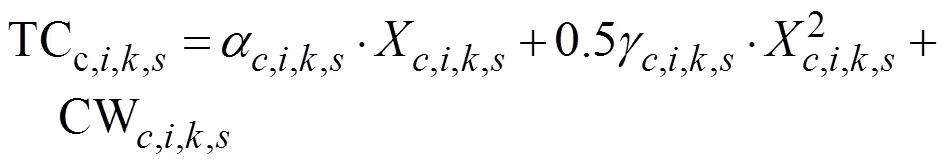

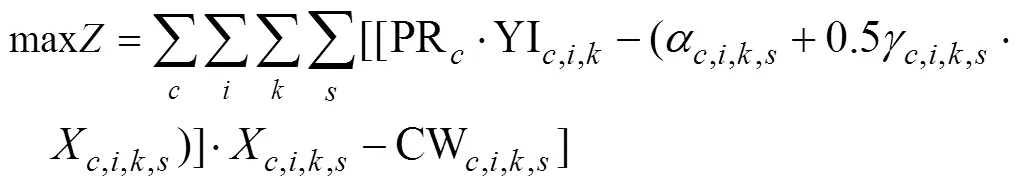
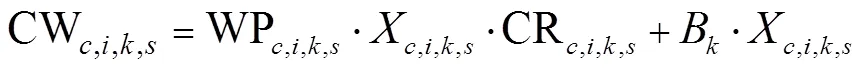
为保证模型的灵活性,去掉校正约束式(3),其他约束和1.2.1节中的模型保持一致,得到含未知参数的新模型。为求解未知参数矩阵α,i,k,s和γ,i,k,s,针对1.2.1节和1.2.2节的模型,利用库恩塔克定理,对式(1)和式(12)求偏导可得:

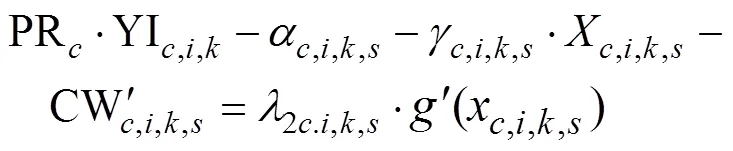
式中1c,i,k,s和2c,i,k,s分别表示校正约束和资源约束对应的对偶值,(x,i,k,s)表示在x,i,k,s点处起作用的校准约束向量,(x,i,k,s)为在x,i,k,s点处起作用的资源约束向量集。
由式(14)和式(15)可以得到

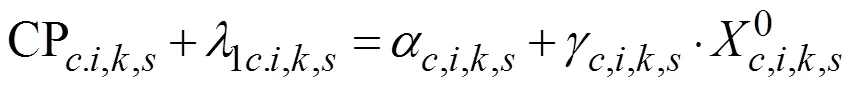
将单位面积成本观察值(不包括灌溉水费)和模型联系起来,使得不同区域不同水源不同作物不同灌溉方式的平均成本与基期成本观察值相等[13,32],则得到
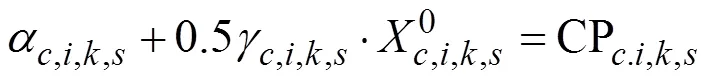
结合式(17)和式(18),可得α,i,k,s和γ,i,k,s的最终值为


将参数α,i,k,s和γ,i,k,s代入式(12)中,可得到校准后的灌区农业水价实证数学规划模型。
基于该模型在基准期的最优解与实际种植面积,对模型进行验证,验证后用于不同水价政策的效应模拟。改变式(2)中水价政策变量WP,i,k,s、B的值,用校准后的模型模拟不同水价政策的实施效果。
2 实证研究
2.1 研究区基本概况
民勤县(102°45′~103°55′E,38°20′~39°10′N)位于甘肃省西北方位,石羊河流域下游(图1),是沙漠中的绿洲,邻近地区的天然生态屏障[33]。民勤县面积1.58万km2,2015年常住人口24.12万,耕地面积5.86万hm2,县内包含红崖山、环河、昌宁3个灌区,主要的粮食作物有小麦和玉米,主要的经济作物有葵花、蔬菜、瓜类、棉花等。主要的水源为地表水、地下水。主要的节水灌溉方式是膜下滴灌和温室滴灌,传统灌溉方式包括畦灌、沟灌、管灌和大水漫灌。
民勤县年均降雨量113 mm,蒸发量2 644 mm,是中国境内最干旱的地区之一。县内长期以种植高耗水粮食作物为主,农业灌溉用水量占总用水量的70%以上,水资源供需矛盾突出。为缓解农业用水紧张的态势,民勤县于2003年开始实施水价改革,逐步提高农业水价。2013年,农业灌溉的地表水价从0.108元/m3调整至0.24元/m3。地下水实行两部制水价,即基本水价与计量水价相结合。其中,基本水价是为维持水利工程单位正常运转而向用水户收取的最低基本费用,按补偿供水工程的直接固投、管理费用和50%的折旧费、修理费的原则制定,以灌溉面积收取水费;计量水价按实际灌溉用水量收取水费。两部制水价制度既能利用基本水价部分使供水成本得到补偿,保证供水工程持续、稳定运转;又能利用计量水价部分防止水资源浪费,促进农业节约用水,目前已在国内外许多大、中型农业灌区实施[34-35]。民勤现行的基本水价为30元/hm2,地下水计量水价为0.235元/m3。此外,2013年武威市和民勤县人民政府分别出台了《武威市人民政府关于深化水价改革的实施意见》(武政发2013 91 号)和《民勤县人民政府关于印发民勤县深化水价改革实施意见的通知》(民政发 2013 109 号),提出推进差别水价的实行[36]。
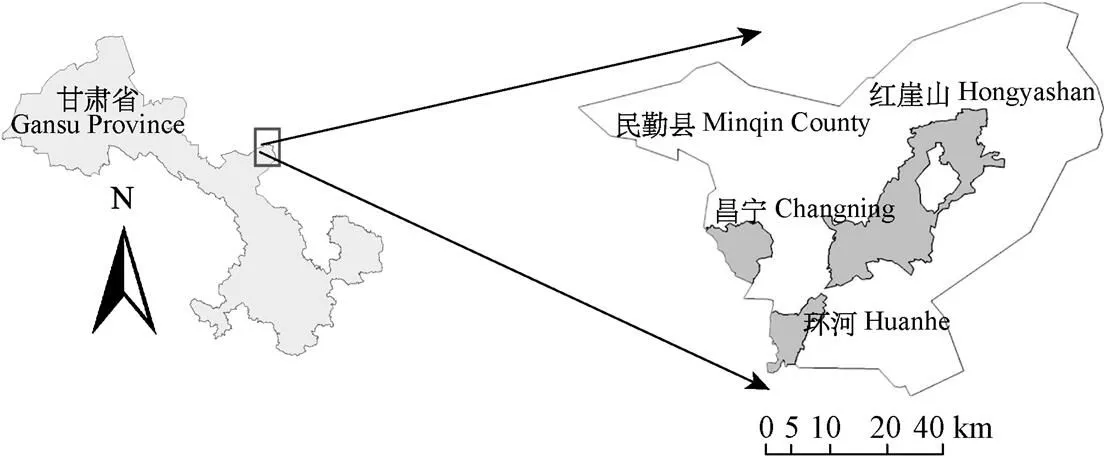
图1 甘肃省民勤县示意图
2.2 情景设置与输入数据
本研究考虑3种水价上涨政策情景,分别为:1)单一水量计价政策情景(以下简称“单一水价情景”):单纯按水量计价;2)两部制水价政策情景(以下简称“两部制水价情景”):按计量水价和基本水价相结合的方式计价;3)两部制水价耦合差别水价政策情景(以下简称“差别水价情景”):在两部制水价的基础上实行差别水价,对于设施农业和实施滴灌的大田节水作物收取较低的水价,对采用传统种植方式的粮食作物收取较高的水价。
为提高政策的公众接受度和易操作度,且为保持效应模拟时的一致性从而更好地反映趋势变化,本模型研究的基本假设和简化如下:1)为促进水价收取的公平性,在研究区实行同样的水价政策;2)由于现行水价政策下地表水和地下水计量水价接近,所以模拟中不区分地下水和地表水价,耕地的基本水价设定为30元/hm2,计量水价部分以现状水价0.24元/m3为起涨点;3)作物灌溉方式分为滴灌和传统灌溉2种,不考虑传统灌溉方式间成本、灌溉用水和作物单产的差异,滴灌灌溉方式主要考虑田间滴灌带的投资成本;4)结合《武威市深化水权水价改革实施意见》和民勤差别水价实施情况,按照上涨后的水价,将滴灌灌溉的水价优惠50%,将传统种植方式下粮食作物的水价上浮50%;5)模拟水价上涨过程中,基本水价以及计量部分差别水价的优惠与上浮幅度不变,仅提升计量部分的水价数值。
本研究基于民勤县2015年的种植面积、种植成本、灌溉用水量、作物产量、人均作物需求量等各项基础数据如表1所示。表中灌溉种植面积和产量数据由查阅《民勤县2015年国民经济和社会发展统计资料汇编》[37]和实地调研得到;作物单价以及成本数据由《2016年全国农产品成本收益资料汇编》[38]获得;单位面积灌溉水量数据由武威市水务局获得。
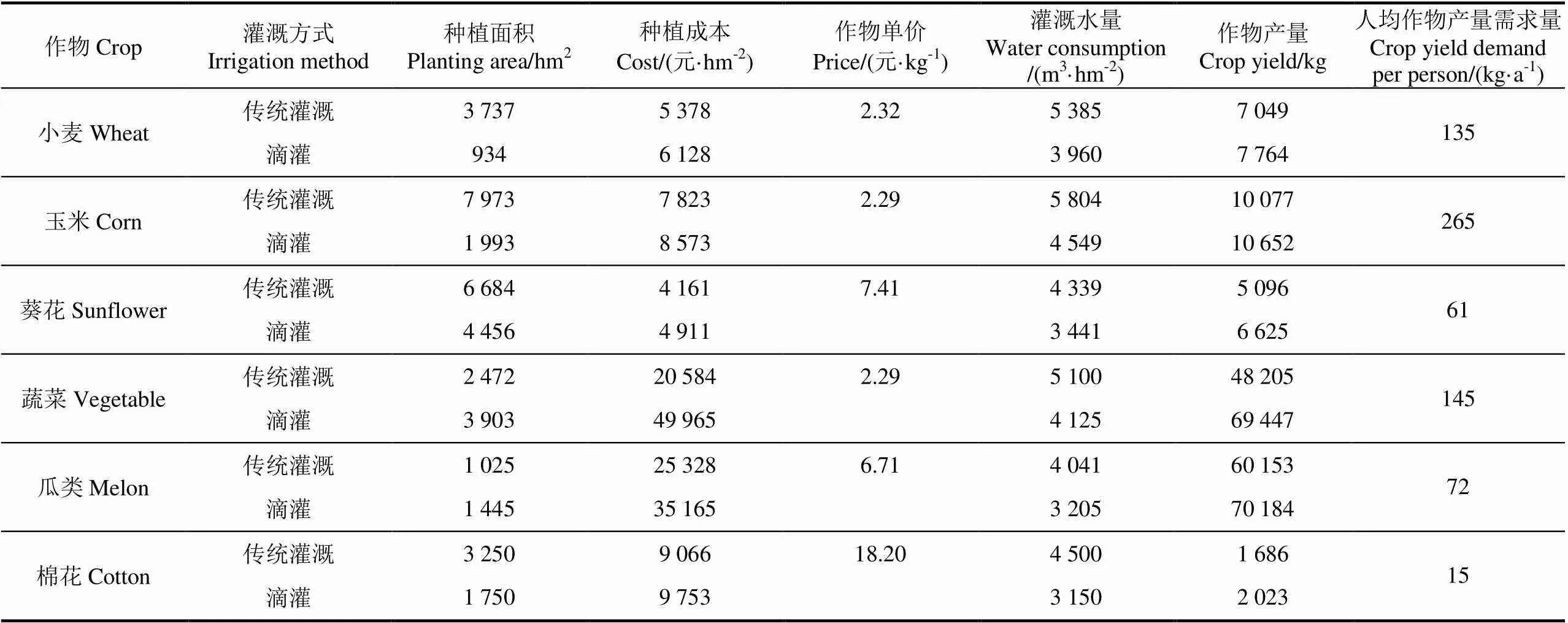
表1 民勤6种作物基础数据
注:传统灌溉方式包括畦灌、沟灌、管灌和大水漫灌。
Note:Traditional irrigation methods include border irrigation, furrow irrigation, pipe irrigation and flood irrigation.
3 结果与分析
3.1 模型率定与验证
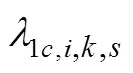

表2 模型校准过程中得到的相关参数
注:差值为种植面积模拟值减去实际值。
Note: Difference is obtained by subtracting actual value from simulated value.
3.2 不同水价制度情景下的结果分析
3.2.1 单一水价情景
计量水价是指仅按水量计算的水价。在该情景中,不存在基本水价,也不考虑不同灌溉方式下的水价差别。则式(2)在该情景中转化为
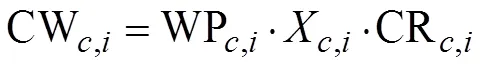
在单一水价情景下对农业水价实证数学规划模型进行求解。6种作物总的和分项的种植面积与滴灌面积比例(即节水灌溉工程面积比例)随水价上升的变化情况分别如图2和图3所示。
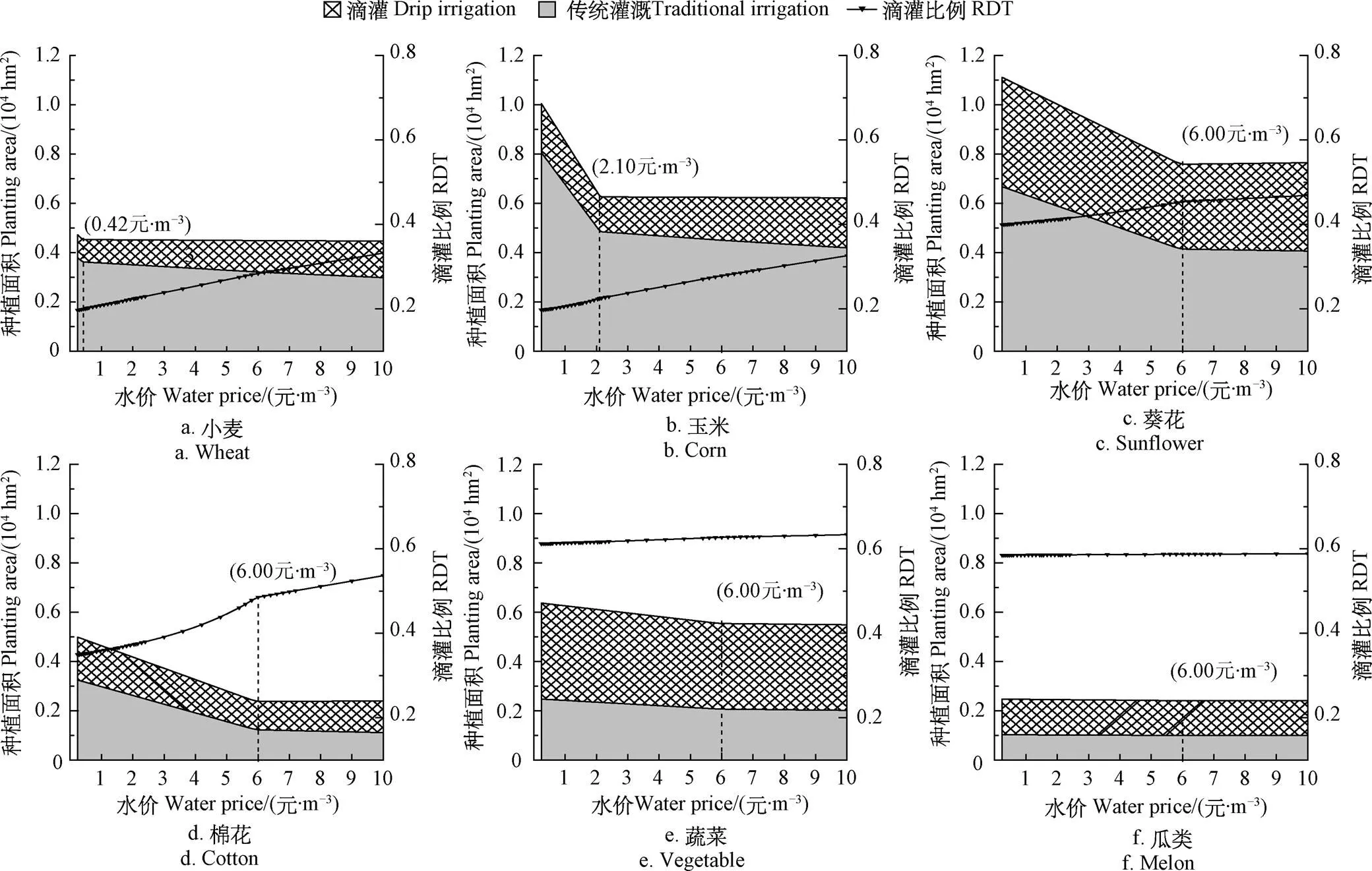
图3 不同作物种植面积和滴灌比例随水价上升变化情况
由图2可知,总种植面积随着水价的升高而减小,当水价升高至6元/m3时,总种植面积减小至最小容许耕地面积28 640 hm2并保持不变。由图3可知,随着总种植面积的减少,各作物的种植面积均有减少。其中,小麦和玉米的种植面积随水价上升会迅速下降,分别在水价为0.42元/m3和2.10元/m3时趋于稳定;葵花和棉花的种植面积随水价的上升逐渐下降,且均在水价达到6元/m3之后趋于稳定;瓜类和蔬菜的种植面积几乎保持不变。这说明为应对水价的上升,农户会选择先压缩低收益的粮食作物的种植面积,再减少高收益的经济作物的种植面积。随着水价的上升,各作物的滴灌面积比例均有上升。其中,棉花的滴灌比例增加最大,小麦、玉米次之,而葵花、蔬菜和瓜类最不明显。这说明,为应对水价的上升,农户会选择增加节水灌溉工程面积比例来减少灌溉用水量。
农户收入、灌溉用水量以及单方水效益随水价上升的变化情况如图4所示。灌溉用水量随水价上升而迅速减少,当水价上升至2.10元/m3时,下降幅度达到17.5%;之后下降过程变得平缓,下降速度不超过之前的1/3;当水价进一步上升到6元/m3后,灌溉用水量基本维持不变,这与总种植面积下降到最小容许面积有关。农户收入随水价的提升匀速下降,当水价为2.10元/m3时,下降幅度达到13.0%。单方水效益随着水价的上升先增加后减小,且在水价为2.10元/m3时达到最高值13.74元/m3,比水价为0.24元/m3时上升了5.5%,之后不断下降。
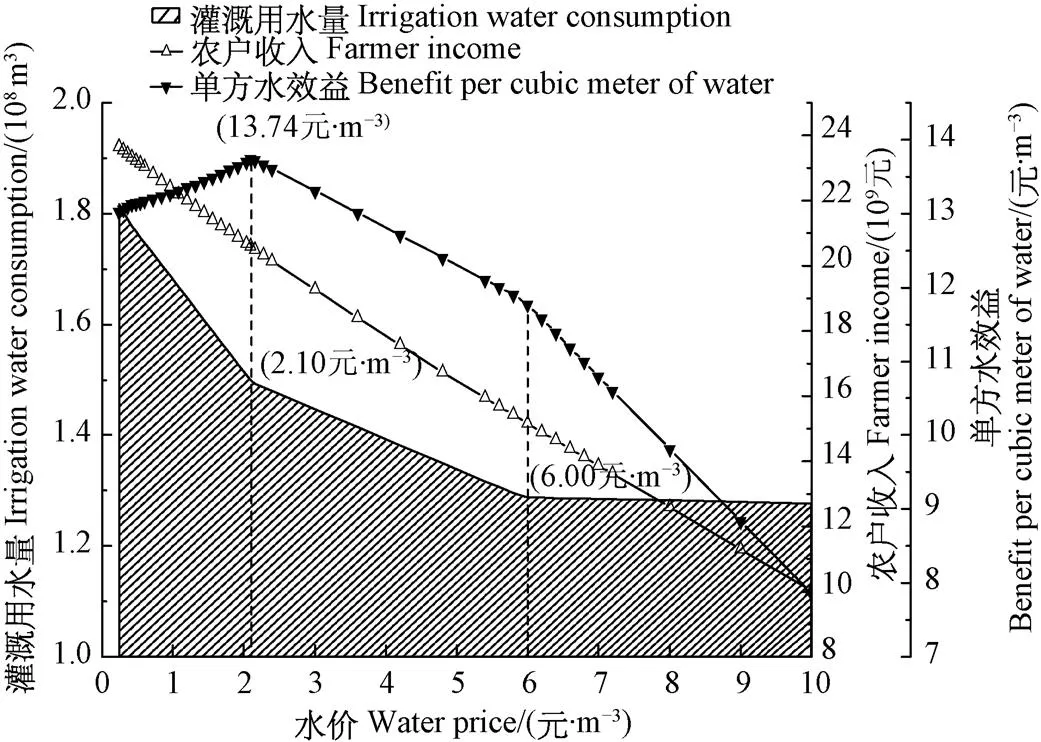
图4 农户收入、灌溉用水量以及单方水效益随水价上升变化情况
结合图2和图4中指标的变化趋势和拐点看出,在水价达到2.10元/m3之前,随着水价的上升,灌溉用水量的减少幅度比农户收入下降的幅度更大,且单方水效益不断上升,占地面积不断减小。而在水价上升至2.10元/m3之后,作物种植面积和灌溉用水量的下降速度显著变低,同时农户收入和单方水效益均不断减小。因此,在单一水价情景下,水价应处于0.24~2.10元/m3之间。
3.2.2 两部制水价情景
两部制水价是指计量水价和基本水价相结合的方式。在该政策情景中,除单一水价情景中的计量水价外,还需按种植面积支付基本水价。其灌溉水费计算公式(21)可转化为
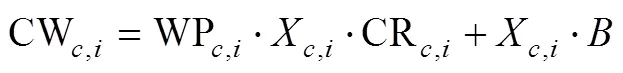
基本水价的加收,会使两部制水价情景下的水价比单一水价情景更高,但由于目前民勤县基本水价收费标准偏低(仅为30元/hm2),其影响较小。总体来说,2种政策的实施效果无显著差别。具体的,两部制水价情景中,随水价的上升,种植面积、滴灌比例、农户收入、灌溉用水量和单方水效益的变化趋势和变化拐点与单一水价情景基本一致。因此,与单一水价情景类似,从占地面积小、灌溉用水省、单方水效益高、对农户收入影响小4个方面考虑,如果实施两部制水价政策,上涨后的水价应处于0.24~2.10元/m3之间。在下述的两部制水价和差别水价情景中,滴灌比例也呈现出与单一水价情景相似的规律。由于基本水价的存在,当计量部分水价相等时,两部制水价情景滴灌比例会高于单一水价情景;差别水价情景因兼有基本水价和对滴灌作物的优惠,其滴灌比例又高于两部制水价。
虽然单一和两部制水价情景下各指标的变化趋势基本一致,但具体的指标值有一定差别(图5)。除单方水效益以外,两部制情景下的总种植面积、灌溉用水量、农户收入和滴灌比例均低于单一水价情景。在作物总种植面积和灌溉用水量方面,2种政策情景的差值呈台阶式变化(图5a和5b)。其中,第1个差值突变台阶始于水价上升至0.42元/m3时,即2种政策下小麦种植面积均下降至稳定水平的节点;第2个差值突变台阶出现在水价进一步上升至2.10元/m3时,此时2种政策下的玉米种植面积均基本稳定、不再下降;第3个突变台阶出现于水价提升至6元/m3时,即2种政策下的总种植面积均降至最小允许值后,差值为0。

图5 两部制水价情景中各指标减去单一水价情景中各指标的差值
这说明,在2种政策下,总种植面积和灌溉用水量随水价上升的下降速度相同,其政策间差值在一般情况下不随水价上升而改变。但在使作物种植面积趋于稳定的水价拐点上,对应作物的种植面积和灌溉用水量差值变为0,这时总种植面积和灌溉用水量差值会发生跳跃式变化,且水价越高、差值越小。
在农户收入方面(图5c),两部制水价情景略低于单一水价情景,但2情景的相差幅度((两部制水价的农户收入-单一水价的农户收入)/两部制水价的农户收入)仅为-0.05%左右,其绝对值低于灌溉用水量和单方水效益相差幅度绝对值。在单方水效益方面(图5c),当水价小于2.10元/m3时,两部制水价情景略高于单一水价情景,其差距在水价为0.36元/m3时出现峰值。然而,当水价达到2.10元/m3后出现逆转,单一水价情景的单方水效益将略高于两部制水价情景,其优势在水价上涨到6元/m3后将进一步加大。
就不同水价水平对应的适宜政策而言,当水价在2.10元/m3以下时,两部制水价政策单方水效益高于单一水价政策,种植面积、灌溉用水量低于单一水价政策,农户收入方面虽低于单一水价政策,但其减少幅度低于灌溉用水量的减少幅度和单方水效益的增加幅度,因此推荐两部制水价政策。若水价需要上涨到拐点2.10元/m3以上,单一水价政策的单方水效益和农户收入要比两部制水价政策更高,且其比两部制水价政策多占的地、多用的水急剧减少,因此推荐单一水价政策。
3.2.3 差别水价情景
该情景在两部制水价政策的基础上实行差别水价,水价随作物灌溉方式和作物种类而不同。将滴灌灌溉的水价优惠50%,将传统种植方式下粮食作物的水价上浮50%。
差别水价情景中,随水价的上升,总种植面积、滴灌比例、农户收入、灌溉用水量和单方水效益的变化趋势与其他2种情景基本一致,但变化拐点不同,且模拟得到的各指标具体值与其他2种情景有所差别。
作物总种植面积和分项种植面积随水价变化情况如图6a所示。在该情景中,小麦和玉米的种植面积分别在水价上升至0.3元/m3和1.50元/m3时下降至稳定不变,与前2种政策情景相比有所提前;而其余作物的种植面积以及总种植面积随水价下降的稳态拐点则出现在水价高达6.80元/m3时,滞后于前2种政策情景。这主要是由于,差别水价政策对采用传统灌溉方式的粮食作物加价,使得粮食作物种植面积易随水价上涨而快速压缩;对采取滴灌的经济作物种植实行优惠政策,使其对水价上涨的响应更为迟缓。
差别水价情景中单方水效益、农户收入和灌溉用水量随水价上升的变化情况如图6b所示。在该情景中,单方水效益在水价上升至1.50元/m3时达到峰值14.00元/m3,相比于起涨点的上升幅度为4.2%;作物总灌溉用水量随水价上升而下降,在水价为1.50元/m3时下降幅度达到14.9%,之后下降速度明显后变慢;农户收入随水价的提升的下降速度波动不大,其在水价上升至1.50元/m3时,下降幅度为9.2%。
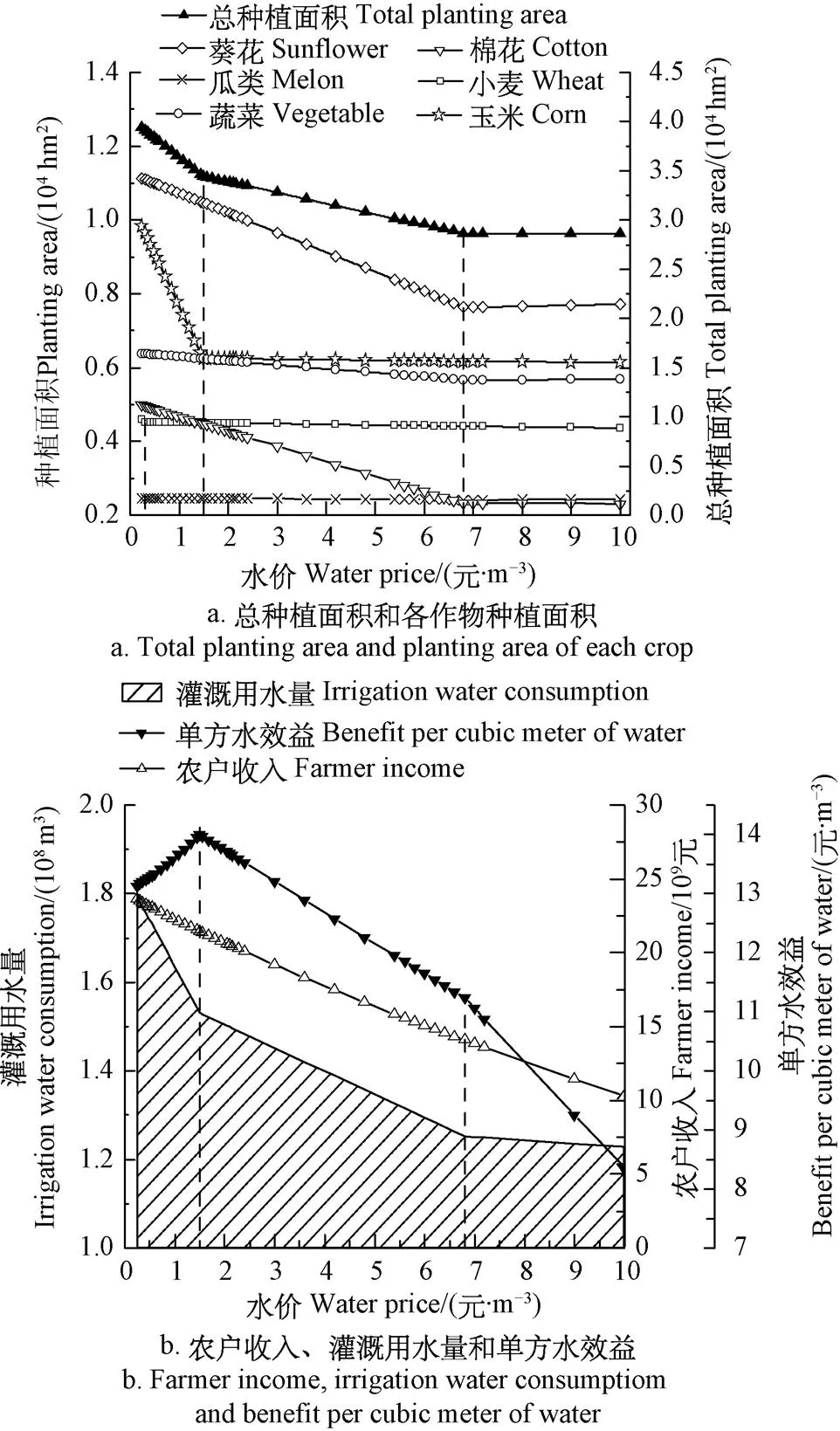
图6 差别水价情景中各指标值随水价上升变化情况
结合图6a和6b中各指标的变化趋势和拐点可以看出,在水价达到1.50元/m3之前,随着水价的上升,虽然农户收入有所下降,但不及灌溉用水量的减少幅度,且单方水效益不断上升,占地面积也不断减小。而在水价上升至1.50元/m3之后,随着水价的上升,农户收入和单方水效益均不断减小,同时作物种植面积和灌溉用水量的下降速度显著放缓。因此,在差别水价情景下,从单方水效益高、占地面积小、灌溉用水省、农户收入影响小四方面考虑,上涨后的水价应处于0.24~1.50元/m3之间。
图7比较了差别水价情景与其他2种水价政策情景的模拟结果。较之其他2种政策情景,当水价少于2.10元/m3时,差别水价情景下总种植面积更小、灌溉用水更省、单方水效益更高;当计量部分水价为2.10~6元/m3时,差别水价情景灌溉用水更多、总种植面积更大、单方水效益和农户收入更低;水价高于6元/m3后,差别水价情景的单方水效益更高、灌溉用水更省、农户收入和种植面积总体来看更高。

注:差值①表示差别水价减去两部制水价得到的各指标差值,差值②表示差别水价减去单一水价得到的各指标差值
综合3种政策情景下的分析结果,当计量部分水价低于2.10元/m3或高于6元/m3时,差别水价政策优于其他2种水价政策;当计量部分水价在2.10~6元/m3之间时,差别水价政策在3种水价政策中最不理想,而单一水价政策最为适宜。就单方水效益而言,差别水价政策在计量部分水价为1.50元/m3时所获得的单方水效益是所有情景中最高的。
4 结 论
针对多水源多灌溉方式的农业灌区,运用实证数学规划模型,构建了农业水价政策效应模拟方法,以水价改革试点区甘肃省民勤县为例,进行实证研究。分别模拟了单一水价、两部制水价以及差别水价3种政策情景之下,研究区农户收入、单方水效益、作物种植面积、灌溉用水量和节水灌溉工程面积比例随水价上升的变化趋势,并在其基础上得到不同水价政策下的水价上涨阈值以及各种政策的适用范围。研究得到的主要结论包括:
1)利用2015年的数据在现状水价政策下对模型进行校准,校准后的模型基准期最优解与实际种植面积的差值绝对值不超过1.03×10-3hm2,模型可用于水价政策效应的模拟。根据模拟结果可得,随着水价的上升,3种水价政策情景下各效应指标变化趋势相似:农户收入不断减少,作物灌溉用水量和作物种植面积先减少后趋于稳定,节水灌溉工程面积比例增加,单方水效益先增加后减少。
2)3种水价政策情景下,为应对水价的上升,农户普遍倾向先减少粮食作物的种植面积,然后再压缩经济作物的面积,还会通过增加作物节水灌溉面积比例来减少灌溉用水量。
3)在单一水价政策和两部制水价政策情景下,上涨后的水价宜处于0.24~2.10元/m3之间;在差别水价政策情景下,上涨后的水价宜处于0.24~1.50元/m3之间。当计量部分水价低于2.10元/m3或高于6元/m3后,差别水价政策的综合效益最高;当计量部分水价位于2.10~6元/m3之间时,单一水价政策最为理想;实行差别水价政策且计量部分水价为1.50元/m3时取得的单方水效益在所有情景中最高。
本文证明了水价在阈值内稳步上涨,不仅不会降低用水的综合效益,反而可以提升单方用水效益。同时,证明了民勤县现行的差别水价政策是合理的。民勤县目前的水价远低于阈值,因此,在未来中短期内,应推进差别水价的实行,计量部分水价应在0.24~1.50元/m3之间逐步上升。在实施差别水价政策的同时,应注意加大对节水灌溉工程的投入,也可考虑制订配套的补贴政策对农户进行适当补偿。
在实际应用中,可在本研究结论的基础上,广泛开展公众参与,并综合考虑当地现有水价、农民支付意愿、政府财政补贴、供水工程收入等多种因素和评判指标得到最终的水价具体实施方案。本研究的方法可广泛应用于其他多水源、多灌溉方式灌区,为其水价政策的制定提供科学依据。
[1] 彭致功,张宝忠,刘钰,等. 基于灌溉制度优化和种植结构调整的用水总量控制[J]. 农业工程学报,2018,34(3):103-109. Peng Zhigong, Zhang Baozhong, Liu Wei, et al. Constraint of total water consumption amount based on optimized irrigation schedule and planting structure ajustment[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(3): 103-109. (in Chinese with English abstract)
[2] 姜秋香,周智美,王子龙,等.基于水土资源耦合的水资源短缺风险评价及优化[J].农业工程学报,2017,33(12):136-143. Jiang Qiuxiang, Zhou Zhimei, Wang Zilong, et al. Risk assessment and optimization of water resources shortage based on water and land resources coupling [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(12): 136-143. (in Chinese with English abstract)
[3] James L D,Lee R R. 水资源规划经济学[M]. 北京:水利电力出版社,1984:358.
[4] 周春应,章仁俊. 农业需水价格弹性分析模型[J]. 节水灌溉,2005(6):24-26. Zhou Chunying, Zhang Renjun. Analytical model for price elasticity of agricultural water demand[J]. Water Saving Irrigation, 2005(6): 24-26. (in Chinese with English abstract)
[5] 王密侠,汪志农,尚虎军,等.陕西关中灌区水费计收方式与水资源合理利用[J]. 农业工程学报,2005,21(增刊1):11-14. Wang Mixia, Wang Zhinong, Shang Hujun, et al. Water fee collecting methods and reasonable utilization of water resources in guanzhong irrigation district of shaanxi province[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(Supp.1): 11-14. (in Chinese with English abstract)
[6] 贾大林,姜文来. 农业水价改革是促进节水农业发展的动力[J]. 农业技术经济,1999,18(5):4-7. Jia Dalin, Jiang Wenlai. Agricultural water price reform is the driving force for promoting the development of water-saving agriculture[J]. Journal of Agrotechnical Economics, 1995, 18(5): 4-7. (in Chinese with English abstract)
[7] 杜荣江,张钧. 水资源浪费的经济学分析与控制对策[J]. 河海大学学报:自然科学版,2007,35(6):722-726. Du Rongjiang, Zhang Jun. Economics analysis of waste of water resources and countermeasures for its control[J]. Journal of Hohai University: Natural Sciences, 2007, 35(6): 722-726. (in Chinese with English abstract)
[8] 李晨洋,于伟铭,陈正锐,等.考虑生态的灌区水资源区间两阶段随机规划模型建立与应用[J]. 农业工程学报,2017,33(21):105-114. Li Chenyang, Yu Weiming, Chen Zhengrui, et al. Two-stage interval parameters water resources model considering ecology and application in irrigation district[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 105-114. (in Chinese with English abstract)
[9] 粟晓玲,宋悦,刘俊民,等. 耦合地下水模拟的渠井灌区水资源时空优化配置[J]. 农业工程学报,2016,32(13):43-51. Su Xiaoling, Song Yue, Liu Junmin, et al. Spatiotemporal optimization allocation of water resources coupling groundwater simulation model in canal-well irrigation district[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(13): 43-51. (in Chinese with English abstract)
[10] 李然,田代贵. 农业水价的困境摆脱与当下因应[J]. 改革,2016,32(9):107-114. Li Ran, Tian Daigui. The dilemma of agricultural water price and its countermeasures[J]. Reform, 2016, 32(9): 107-114. (in Chinese with English abstract)
[11] 马超. 农业水价需求弹性调查及政策建议[J]. 水利发展研究,2018,18(4):7-9,13. Ma Chao. Agricultural water price demand flexibility survey and policy suggestions[J]. Water Resources Development Research, 2018, 18(4): 7-9, 13. (in Chinese with English abstract)
[12] Espey M, Espey J, Shaw W D. Price elasticity of residential demand for water: A meta-analysis[J]. Water Resources Research, 1997(33): 1369-1374.
[13] 裴源生,方玲,罗琳. 黄河流域农业需水价格弹性研究[J]. 资源科学,2003,25(6):25-30. Pei Yuansheng, Fang Ling, Luo ling. Price elasticity of agricultural water demand in China[J]. Resources Science, 2003, 25(6): 25-30. (in Chinese with English abstract)
[14] 严冬,周建中. 水价改革及其相关因素的一般均衡分析[J]. 水利学报,2010,41(10):1220-1227. Yan Dong, Zhou Jianzhong. A general equilibrium analysis of water price reform and related factors[J]. Journal of Hydraulic Engineering, 2010, 41(10): 1220-1227. (in Chinese with English abstract)
[15] 赵永,窦身堂,赖瑞勋. 基于静态多区域CGE模型的黄河流域灌溉水价研究[J]. 自然资源学报,2015,30(3):433-445. Zhao Yong, Dou Shentang, Lai Ruixun. Research on agriculture water pricing in the yellow river basin based on static multi-region CGE model[J]. Journal of Natural Resources, 2015, 30(3): 433-445. (in Chinese with English abstract)
[16] Bartolini F, Bazzani G M, Gallerani V, et al. The impact of water and agriculture policy scenarios on irrigated farming systems in Italy: An analysis based on farm level multi-attribute linear programming models[J]. Agricultural Systems, 2007(93): 90-114.
[17] Howitt R E. Positive mathematical programming [J]. American Journal of Agricultural Economics, 1995, 77(2): 329-342.
[18] 王裕雄,肖海峰. 实证数学规划模型在农业政策分析中的应用:兼与计量经济学模型的比较[J]. 农业技术经济,2012,31(7):15-21. Wang Yuxiong, Xiao Haifeng. The application of positive mathematial programming model in agricultural policy analysis: comparison with econometric model[J]. Journal of Agrotechnical Economics, 2012, 31(7): 15-21.(in Chinese with English abstract)
[19] Heckelei T, Britz W. Models based on positive mathematical programming: State of the art and further extensions [C]. 89th EAAE Seminar Paper, Parma, 2005:48-73.
[20] Merel P, Howitt R. Theory and application of positive mathematical programming in agriculture and the environment [J]. Annual Review of Resource Economics, 2014(6): 451-470.
[21] Iglesias E, Blanco M. New directions in water resources management: The role of water pricing policies [J]. Water Resources Research, 2008, 44(6): 1-11.
[22] Gallego-Ayala J, Gomez-Limon J A. Irrigation water pricing instruments: A sustainability assessment[J]. Spanish Journal of Agricultural Research, 2011, 9(4): 981-999.
[23] Gallego-Ayala J. Selecting irrigation water pricing alternatives using a multi-methodological approach[J]. Mathematical and Computer Modelling, 2012, 55(3/4): 861-883.
[24] Watto M A, Mugera A W. Irrigation water demand and implications for groundwater pricing in Pakistan[J]. Water Policy, 2016, 18(3): 565-585.
[25] Chebil A, Frija A, Thabet C. Irrigation water pricing between governmental policies and farmers' perception: Implications for green-houses horticultural production in Teboulba (Tunisia)[J]. Agricultural Economics Review, 2010, 11(2): 44-54.
[26] Franco-Crespo C, Viñas J M S. The impact of pricing policies on irrigation water for agro-food farms in Ecuador[J]. Sustainability, 2017 9(9): 1515.
[27] Heady E O, Egbert A C. Regional programming of efficient agricultural production patterns[J]. Econometrica, 1964, 32(3): 374-386.
[28] Martin L J, Meister A D, Chen C C, et al. Quadratic programming models applied to agricultural policies[J]. American Journal of Agricultural Economics, 1979, 61(3): 586-587.
[29] Arfini F, Donati M, Solazzo R. Positive Mathematical Programming[M]. Roma, Italy: Research and Economics, 2016.
[30] 田聪颖,肖海峰. 目标价格补贴与生产者补贴的比较:对我国大豆直补方式选择的思考[J]. 农业经济问题,2018,39(12):107-117. Tian Chongying, Xiao Haifeng. Comparison between target price subsidy and producer subsidy: Reflection on the selection of China's soybean direct subsidy[J]. Issues in Agricultural Economy, 2018, 39(12): 107-117. (in Chinese with English abstract)
[31] 中国营养学会. 中国居民膳食指南(2016)[M]. 北京:人民卫生出版社,2016:269-287.
[32] Howitt R E. A Calibration method for agricultural economic production model[J]. Journal of Agricultural Economics, 1995, 46(2): 147-159.
[33] 谢臻,张凤荣,王瀚巍,等. 基于节水灌溉技术的民勤绿洲土地利用空间布局和利用方式调整[J]. 中国农业大学学报,2017,22(10):65-74. Xie Zheng, Zhang Fengrong, Wang Hanwei, et al. Adjustment of land use spatial structure and use pattern based on modern agriculture in Minqin oasis[J]. Journal of China Agricultural University, 2017, 22(10): 65-74. (in Chinese with English abstract)
[34] 柯珊珊,赵伟,杨晴. 水利工程现行水价分析[J]. 水利规划与设计,2017,30(7):161-165. Ke Shanshan, Zhao Wei, Yang Qing. Current water price analysis of water conservancy projects[J]. Water Resources Planning and Design, 2017, 30(7): 161-165. (in Chinese with English abstract)
[35] 王春艳,张博,沈大军. 淠河总干渠供水成本分析计算及两部制水价设计[J]. 水利经济,2012,30(5):30-33. Wang Chunyan, Zhang Bo, Shen Dajun. Calculation of water supply costs and design of two-part water price for main canal of Pihe river[J]. Journal of Economics of Water Resources, 2012, 30(5): 30-33. (in Chinese with English abstract)
[36] 张丽霞. 民勤县农业水价综合改革现状分析及思考[J]. 南方农业,2017,11(30):61-65. Zhang Lixia. Analysis and thinking on the current situation of comprehensive reform of agricultural water price in Minqin county[J]. South China Agriculture. 2017, 11(30): 61-65. (in Chinese with English abstract)
[37] 民勤县统计局民勤调查队. 民勤县2015年国民经济和社会发展统计资料汇编[M]. 甘肃:民勤县统计局,2016:110-120.
[38] 国家发展和改革委员会价格司. 全国农产品成本收益资料汇编2016[M]. 北京:中国统计出版社,2016:21-81.
Simulation of effects of agricultural water price policy based on positive mathematical programming
Tan Qian, Wang Shuping, Zhang Tianyuan
(100083,)
Rational water price policy is of great significance for the efficient use of water resources. However, development processes of water price policy are mostly subjective and few methods are suitable to quantify policy effects. In this study, we focused on irrigation areas with multiple water sources and irrigation techniques. A method based on positive mathematical programming (PMP) was proposed to simulate the impacts of agricultural water price policy on economic benefits of water use, irrigation water consumption, planting land occupation and water-saving irrigation area. This method was applied to address a case in Minqin County, Gansu Province. Under the current water price policy of the study area, the model was calibrated with the actual data in 2015, the absolute value of the difference between the optimal solution of the calibrated model and the actual planting area in the base year didn’t exceed 1.3×10-3hm2, indicating that the model was reliable to simulate the effect of water price policy. Subsequently, the model was used to simulate the change trend of index with the rise of water price under the volumetric water price policy, the 2-part water price policy and the differential water price policy. The simulation results showed that, with the rise of water price, the change trend of index under 3 water price policy was similar:the farmer income reduced, the irrigation water consumption and planting area reduced first and then stabilized, the water-saving irrigation area increased, and the benefit per cubic meter of water increased first and then decreased. Simultaneously, in response to rising water price, farmers tended to reduce the planting area of food crops first and then the area of cash crops to alleviate the loss of income. Based on the simulation results, the water price threshold under different policies and the scope of application of various policies were further analyzed, and the following conclusions were drawn. Under the volumetric water price and the 2-part water price policy, the water price should be between 0.24 yuan/m3-2.10 yuan/m3; under the differential water price policy, the water price should be between 0.24-1.50 yuan/m3; when the metering part of the water price was lower than 2.10 yuan/m3or higher than 6 yuan/m3, the comprehensive benefit of the differential water price policy was the highest; when the metering part of the water price was between 2.10 yuan/m3and 6 yuan/m3, the volumetric water price policy was the most ideal; when the differential water price policy was implemented and the metering part of the water price was 1.50 yuan/m3, the benefit per cubic meter of water was the highest. This paper confirmed that the steady increase of water price would not reduce the comprehensive benefits of water use, but increase the benefit per cubic meter of water. The differential water price policy currently implemented in Minqin County was appropriate. In the future, in Minqin County, the water price under the differential water price policy should be increased within the range of 0.24-1.50 yuan/m3. Moreover, during the course of water price rising in the study area, special attentions should be paid to increase investment in water-saving irrigation projects and farmer income subsidy policies should be established under local contexts. Based on the conclusions of this study, various local factors and evaluation indexes such as current water price, farmers' willingness to pay, government financial subsidies, and income from water supply projects, could be comprehensively considered to obtain detailed implementation plan of water price policy. The method established in this paper was also applicable to other areas with similar problems.
agriculture; water; models; positive mathematical programming; water price policy; economic benefits of water use
2019-03-10
2019-07-10
国家自然科学基金资助项目(51822905、51779255);国家千人计划青年项目
谭 倩,教授,博士生导师,主要从事水资源水环境系统分析方面的研究。Email:qian_tan@cau.edu.cn
10.11975/j.issn.1002-6819.2019.16.018
S607+.1
A
1002-6819(2019)-16-0161-11
谭 倩,王淑萍,张田媛.基于实证数学规划模型的农业水价政策效应模拟[J]. 农业工程学报,2019,35(16):161-171. doi:10.11975/j.issn.1002-6819.2019.16.018 http://www.tcsae.org
Tan Qian, Wang Shuping, Zhang Tianyuan. Simulation of effects of agricultural water price policy based on positive mathematical programming[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(16): 161-171. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.16.018 http://www.tcsae.org

