水轮机尾水管涡带压力脉动同步及非同步特性研究

孙龙刚 郭鹏程 罗兴锜

(西安理工大学省部共建西北旱区生态水利国家重点实验室， 西安 710048)

0 引言

随着风能、太阳能等间歇性能源在电网中比例的增加，水电机组将更多地运行在变负荷工况及偏工况下以平衡电网参数[1-2]。偏工况下运行，水轮机不可避免地经历动态负荷不平衡，激发高幅值压力脉动、水力振动、噪声等，严重影响水轮机运行稳定性[3-5]。尾水管涡带(Precessing vortex rope,PVR)是混流式水轮机在部分负荷工况运行时尾水管水流中出现的一种强烈偏心螺旋状涡旋运动，涡带频率约为转频0.2～0.45倍并激发高幅值压力脉动。尾水管涡带的形成有两个主要因素：较大的角动量与轴向动量比产生的强烈涡旋流动；与转轮出口速度及锥管段扩散形式有关的轴向方向逆压梯度[6]。它是混流式水轮机运行在偏工况下的一种固有水力特性，是水力不稳定性的表征和结果，严重时会影响运行稳定性及造成疲劳破坏等，因此部分负荷工况下尾水管内的压力脉动特性研究受到学者持续关注[7-10]。

2000年，EUREKA(欧洲研究协调局)发起了FLINDT(Flow investigation in draft tube)研究项目[11]，旨在建立较大运行范围的试验数据库进行CFD计算的比较和确认。文献[12]对混流式转轮出口涡旋流动进行了试验和理论研究，以阐明尾水管压力恢复系数出现突降的原因。文献[13]用涡旋生成装置模拟混流式水轮机在部分负荷下的运动，并对涡旋流动进行了LDA(激光多普勒测速仪)测试和数值模拟研究。数值计算分别采用DDES(延迟分离涡)-SA(Spalart-Allmaras)模型和RNGk-ε模型，结果表明两种湍流模型预测的平均速度与试验测试比较一致，而DDES-SA模型在最大与最小转速工况的精度要更高。FLINDT项目的研究，有助于理解混流式水轮机弯肘型尾水管内部流动特征及流动机理。

部分负荷工况下，模型试验观测到的螺旋形涡带在尾水管内同时具有轴向及周向运动，因此可将尾水管涡带压力或者速度脉动分解为同步分量和非同步分量，其中同步分量表示涡带突进(PVR plunging)，非同步分量表示涡带旋转(PVR rotating)，分别表征涡带在尾水管锥管段轴向及径向的运动强度[14-15]，一些学者也对此进行了研究[16-18]。

由此可见，尾水管涡带压力脉动的同步及非同步分解，不仅有助于对涡带运动过程直观深入的理解，而且对于抑制以及改善部分负荷工况下尾水管涡带的不利影响具有重要意义。然而，有关研究相对较少且仅进行了简单的流动特征描述。基于此，本文以某混流式模型水轮机为研究对象，开展部分负荷工况下尾水管内部流动特性的试验测试和数值模拟研究，分析涡带周期性演化过程及其诱导的压力脉动特性，将时变压力脉动进行同步及非同步分量的数学分解，对涡带形成过程中同步及非同步运动分量的影响进行动力学分析，进一步理解尾水管涡带的复杂流动特征及其动力学特性。

1 尾水管压力脉动研究方法

1.1 流动控制方程及SST k-ω模型

非稳态的雷诺时均(Reynolds average Navier-Stokes equations,RANS)方程为[19]

(1)

式中t——时间ρ——流体密度

p——压力ν——涡粘度

xi、xj——笛卡尔坐标i、j方向位移

Ui、Uj——i、j方向上的时均速度

u′i、u′j——i、j方向上的脉动速度

采用SSTk-ω湍流模型来封闭式(1)，即

(2)

式中νt——湍动涡粘度

Sij——变形率张量

δijk——Kronecker算子

SSTk-ω湍流模型中湍动能及比耗散率的输运方程为[20]

(3)

(4)

其中

式中k——湍动能ω——比耗散率

F1、F2——混合函数

Pk——湍动生成项

α、α1、β、β*、σk、σω、σω2——方程闭合系数

SSTk-ω湍流模型在边界层使用k-ω湍流模型，在其余区域应用k-ε湍流模型，可较好地捕捉叶轮机械的流动分离现象[21-23]。

1.2 计算域离散及边界条件

本文研究对象为一转轮直径Dm=0.35 m的混流式模型水轮机，如图1所示。该模型由进口到出口分别为蜗壳、活动导叶、固定导叶、转轮以及尾水管，其中固定导叶与活动导叶数均为24，转轮叶片数为15。额定工况下，活动导叶开度σ=24°，单位流量与单位转速分别为Q11=0.933 0 m3/s，n11=73.43 r/min，对应的原型水轮机水头Hp=71.0 m，输出功率PP=228.22 MW。

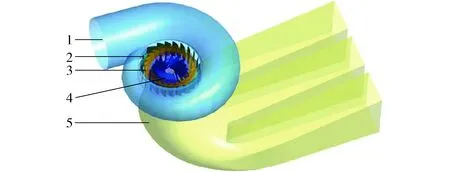
图1 模型水轮机示意图Fig.1 Sketch of investigated model Francis1.蜗壳 2.固定导叶 3.活动导叶 4.转轮 5.尾水管

采用多块结构化六面体网格对蜗壳进口至尾水管出口计算域进行网格离散。为研究网格数目对计算结果的影响，采用美国机械工程师协会(American Society of Mechanical Engineers，ASME)推荐的网格收敛指数(GCI)[24-26]进行网格离散误差的估计。GCI是一个具有95%置信区间、表示两个对比网格中更密网格与渐进值之间距离的指标，可用于预测进一步的网格细化对求解的影响。GCI网格无关性验证需要3套不同数目的网格，分别为细密网格(Fine)、中等网格(Medium)和粗糙网格(Coarse)，计算的近似相对误差、外推相对误差以及网格收敛指数公式为

(5)

式中ea、eext——近似相对误差和外推相对误差

φ——选择的关键变量

φext——关键变量的外推值

r——网格加密因子

m——采用定点迭代法计算的表观级数

下标1、2对应于网格Fine和Medium，下标21为网格Fine对Medium的相对值。

网格Medium相对于Coarse的计算过程与式(5)相同。表1(N1～N3表示3种不同密度的网格数，下标3对应于网格Coarse，下标32为网格Medium对Coarse的相对值)列出了最优工况下数值计算离散误差的计算过程及统计。数值计算蜗壳进口给定质量流量，尾水管出口指定静压，固壁面均采用光滑、无滑移边界条件。瞬态计算动静交界面为“Transient rotor-stator”，对流采用高阶求解格式，瞬态模型则采用二阶向后欧拉模式，收敛标准设为最大残差小于0.001。为消除变量之间代数运算带来的误差，选择直接测得的两个变量转轮扭矩和活动导叶与转轮之间无叶区测点的压力作为网格无关性测试的关键变量。

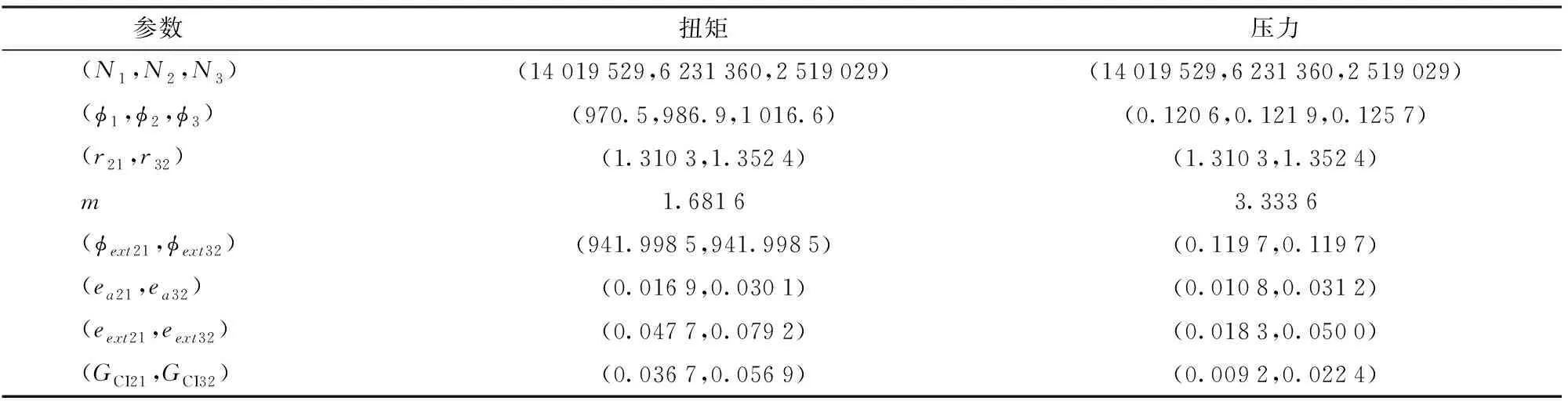
表1 数值计算离散误差及不确定性统计Tab.1 Statistics for discretization error and uncertainties in numerical solutions

由表1可知，3种密度的网格以渐进形式收敛，表明网格加密有利于平均流场的求解。对Fine和Medium网格而言，计算的扭矩不确定度分别为3.67%和5.69%，转轮扭矩不确定度为0.92%和2.24%。为了平衡计算精度与计算资源之间的关系，本文最终选择了Medium网格进行数值计算。图2所示为蜗壳、固定导叶及活动导叶、转轮和尾水管网格示意图。其中蜗壳、固定导叶、活动导叶、转轮及尾水管最大y+值(y+表示第1层网格距离壁面的无量纲距离)分别为135.6、60.8、50.2、56.2和58.6。

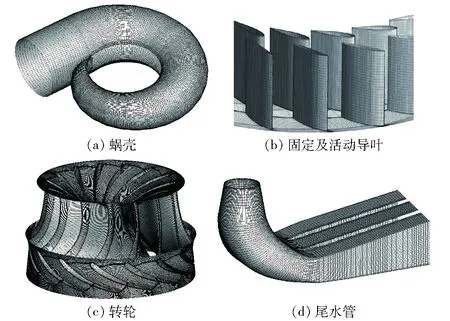
图2 网格生成示意图Fig.2 Grid views for simulation domain

1.3 数值计算方法的试验验证

数值计算与试验测试工况为模型水轮机额定功率的42.35%，对应的活动导叶开度σ=20°，单位转速n11=88.00 r/min，单位流量Q11=0.745 2 m3/s。水轮机测试试验台如图3a所示，试验过程中采用电磁流量计记录流量，压差传感器用来测量蜗壳进口与尾水管出口之间的压差来计算水头。为了捕捉尾水管涡带压力脉动，两个径向相差180°的微型压力传感器S201和S209被嵌入式安装在尾水管锥管段壁面，以记录时变压力脉动的动态变化过程。模型试验严格按照IEC60193试验标准进行水力效率、流量的测量以及传感器标定[27]。试验前仔细检查传感器的精度和标定不确定度，流量计、压差传感器以及压力传感器的估计不确定度分别为±0.18%、±0.05%和±1%，模型试验台水力效率的随机误差与系统误差分别为±1%和±0.214%。

除测点S201和S209外，数值计算额外监测尾水管锥管段4个不同高度断面上的压力变化，如图3b所示。4个断面分别命名为S1、S2、S3和S4面，分别位于锥管段Z=-0.206 m、Z=-0.254 m、Z=-0.361 m和Z=-0.467 m，其中S2面为尾水管进口以下0.3D2(D2为转轮出口直径)处。在S2面上，锥管段壁面上逆时针间隔22.5°布置了16个测点，依次命名为S201～S216；锥管段内部沿X方向分别布置7个测点，依次命名为S217～S223，其余3个平面按照相同的方法布置对应的测点。

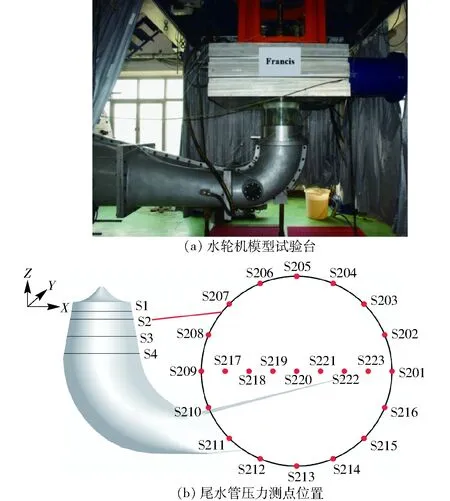
图3 水轮机模型试验台及数值计算压力测点位置Fig.3 Model test for Francis turbine and minoring point locations

统计得到尾水管涡带压力脉动幅值及主频数值解与试验测试的对比结果。其中，压力脉动幅值采用线性计算，为压力最大值与最小值之差的97%置信区间，频率为快速傅里叶变换(FFT)获得的主频。试验测得的幅值为11.398%，对应的数值解为11.09%，计算误差约为2.70%。试验测试压力信号经FFT变换后的主频为0.256fn(fn为转频)，为典型的尾水管涡带压力脉动频率，数值预测的主频为0.249 3fn，对应的计算误差为2.62%。对比结果可知，数值计算获得的压力脉动主频及幅值与试验值比较吻合，误差在可接受范围之内，且在涡带频率上的预测精度略高于压力脉动幅值。

2 结果分析

2.1 压力脉动特性

图4(图中Cp表示压力脉动系数，f表示频率)为锥管段S2平面上沿X轴上5个测点S209、S217、S218、S219、S220的压力变化曲线及对应的FFT变换。图5(图中T表示尾水管涡带运动周期)以S2面为例，给出了一个周期内涡带运动对平面压力的影响示意图，图中同时给出了图4中5个测点的位置分布。压力脉动系数计算公式为

(6)

pBEP——最优工况参考压力

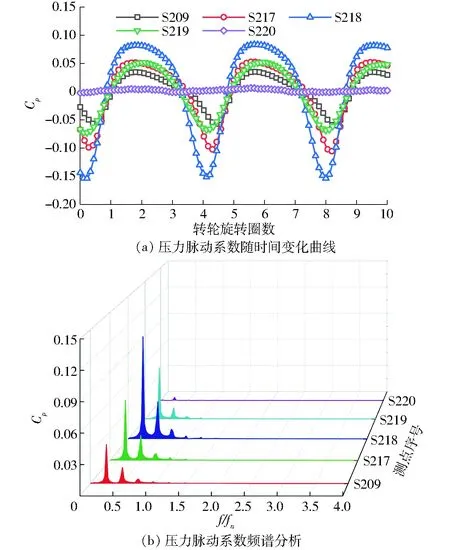
图4 X轴测点时变压力曲线及频谱分析Fig.4 Temporal variation of numerical pressure coefficient and spectral analysis along X axis

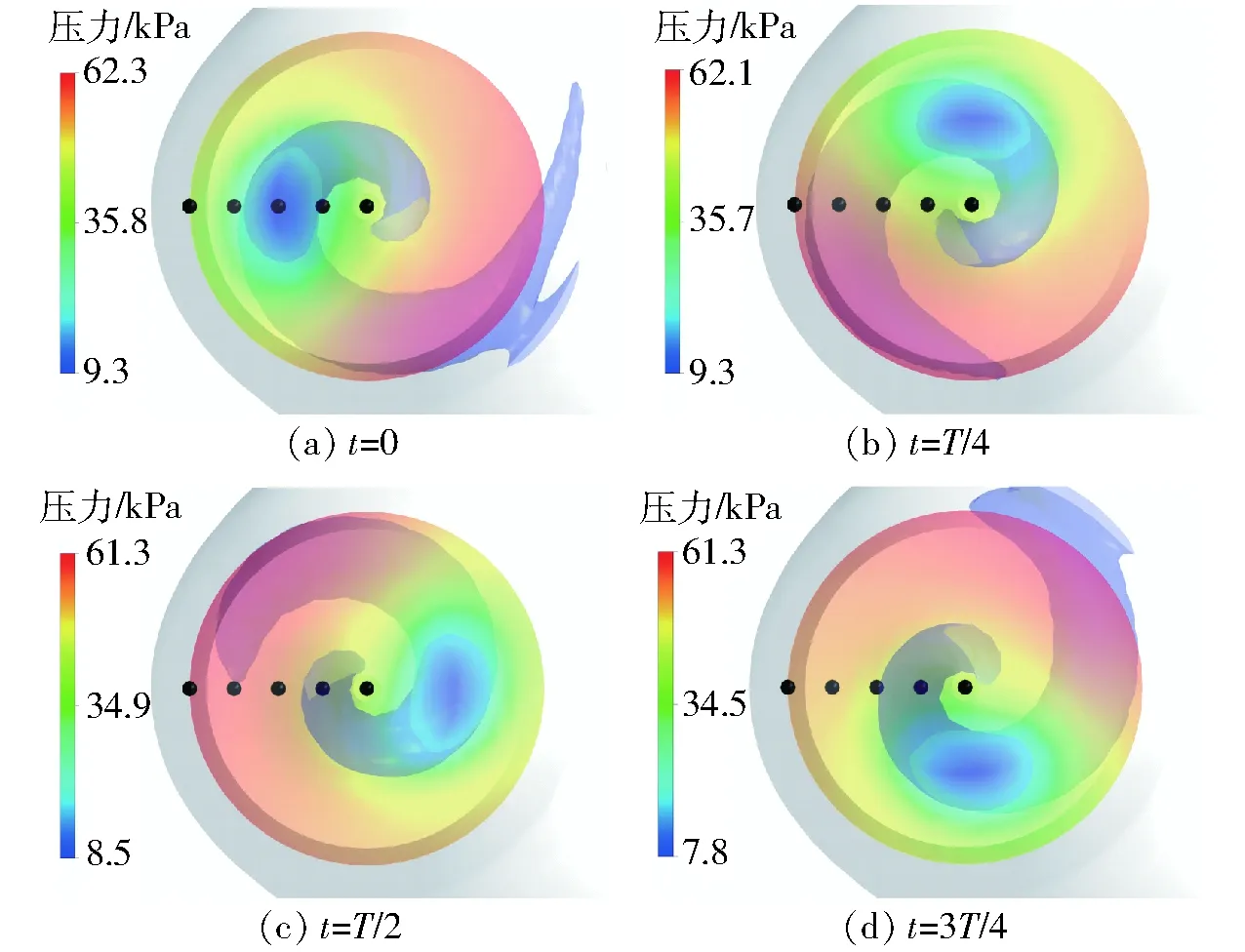
图5 进动涡带对平面压力的影响Fig.5 Influence of precessing vortex rope on pressure distribution

由图4时变压力及其FFT变换结果可知，转轮旋转10圈时间内，尾水管内压力呈周期性低频波动，FFT变换后各个测点上的主频均为0.25fn，为典型的尾水管涡带频率。不同测点上压力脉动幅值差异较大，幅值从大到小依次为S218、S217、S219、S209、S220。除转轴中心测点S220外，造成其他测点幅值差异的原因，可以用图5解释。如图5所示，部分负荷工况下椭圆形偏心涡带的出现，对整个压力场有直接影响。涡带中心压力最低，压力由最低点向外部辐射增加，且涡带所在一侧压力较低，对应的另一侧压力较高，即当涡带扫过测点时，其压力最低。因此，涡带旋转运动对压力场带来的影响表现为与涡带中心距离越近，测点幅值越大。由图5可知，S218位于涡带运动轨迹上，其幅值最大；S217与S219位于涡带两侧，其幅值小于S218，同理，壁面测点S209幅值小于S217和S219。对于测点S220，其位于转轴中心，涡带工况下锥管段中心一般为回流及死水区，故脉动幅值较小。

2.2 压力脉动同步及非同步分解

尾水管锥管段内的水流流动，同时具有周向旋转运动和轴向竖直运动，为定量分析这两种运动，可将尾水管内的压力信号分解为同步分量(Synchronous component)及非同步分量(Asynchronous component)[15,28-29]，公式为

(7)

(8)

式中Asyn、Aasyn——同步分量及非同步分量

A1、A2——尾水管锥管上关于水轮机轴对称的压力监测信号

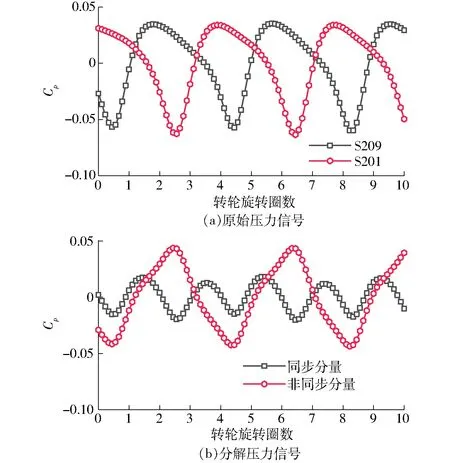
图6 原始及分解后压力信号Fig.6 Original and decomposed pressure signals

以测点S209与S201为例，图6为压力脉动系数以及分解后压力脉动系数的同步分量、非同步分量随时间变化曲线，图7为同步与非同步分量压力脉动系数频谱分析结果。

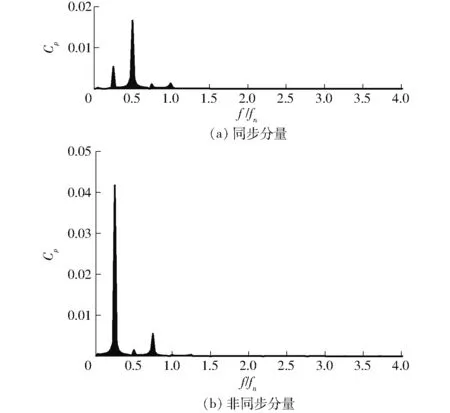
图7 同步及非同步分量压力脉动频谱分析Fig.7 Spectrum analysis of synchronous and asynchronous components

由图6可知，两个原始信号其脉动频率及幅值均一致，仅在相位上有差别；分解后的压力信号，非同步分量幅值绝对占优，其压力脉动幅值约为同步分量的2.51倍，并且非同步分量对原始信号具有依从性，即其主频保持与原始信号一致，均为0.25fn，为低频涡带频率，而由于原始信号波峰波谷间存在相位差，经过压力分解后的同步分量主频发生变化，约为0.50fn。

为进一步量化锥管段不同高程上同步与非同步分量幅值，以及研究其沿轴向和周向运动的演化规律，图8a给出了S2平面上压力脉动幅值沿圆周方向的极轴分布图，为图3b中S2平面上S201至S216测点压力脉动系数幅值沿圆周方向的拟合。该拟合曲线与等压力脉动系数曲线呈偏心圆分布，定义极轴图圆心与拟合圆圆心之间距离OO′为该平面上的压力脉动系数的同步分量幅值，拟合圆半径O′D为压力脉动系数的非同步分量幅值。采用相同的处理方法，图8b为锥管段4个不同高度截面上压力脉动系数同步及非同步分量比较直方图。

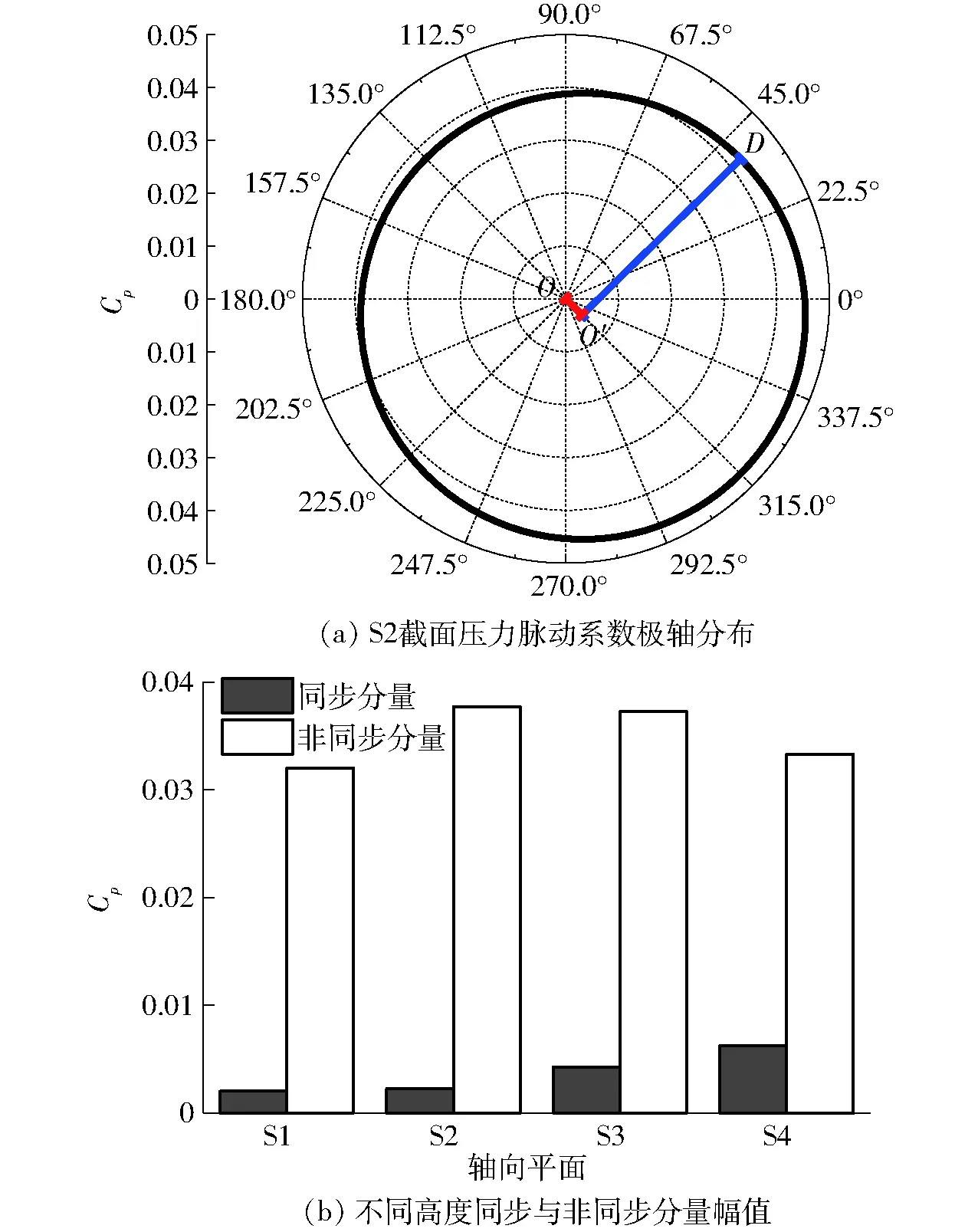
图8 压力脉动同步与非同步分量幅值比较Fig.8 Comparison of pressure amplitude of synchronous and asynchronous components

由图8b比较分析可知，锥管段不同高度上非同步分量幅值均绝对占优，同步分量与非同步分量之间的比值约为0.063、0.060、0.114、0.188，表明当尾水管中出现螺旋形涡带时，锥管段内作螺旋状涡旋运动的水流占主导作用。非同步分量由尾水管进口首先增大，在S2平面上达到最大值，然后减小，而表征压力轴向运动的同步分量，其幅值沿流动方向逐渐增大。

3 结论

(1)研究了涡带诱发的高幅值压力脉动特性并对涡带压力脉动进行同步与非同步分量的数学分解。数值模拟与试验测试均在42.35%额定功率下进行。数值仿真采用瞬态全通道计算，利用GCI技术进行网格无关性验证并确定网格数目，最终获得了与试验测试压力脉动主频及幅值结果一致的数值解。

(2)尾水管内出现进动涡带时，锥管段内不同测点均呈低频周期性脉动，预测的脉动主频为0.25fn，为典型的尾水管涡带频率。由于涡带中心为低压区，涡带所在一侧压力较低，对应的另一侧压力较高，故距离涡带运动轨迹越近的位置，其压力变幅越大，导致压力脉动幅值高于周围位置。

(3)将涡带压力脉动分解为同步分量与非同步分量，分解后的压力信号，非同步分量压力脉动幅值较高，且保持了与原始信号一致的0.25fn主频。同步分量主要受原始信号波峰波谷间相位差的影响，其主频发生变化。沿流动方向非同步分量压力脉动幅值首先增大，然后减小，而表征压力轴向运动的同步分量，其幅值逐渐增大。