多个耦合星型网络的同步优化*

舒睿 陈伟 肖井华

(北京邮电大学理学院,北京 100876)

1 引 言

自20世纪末发现复杂网络中的小世界和无标度特性后,复杂网络的相关研究引起了越来越多学者的关注[1−4].自然界中存在许多的复杂网络,例如因特网、人际关系网、电力网、交通网等.复杂网络可以作为神经科学[5]、模式识别[6]、化学[7]、生物[8]、天气[9−11]等系统的网络模型.在无标度网络提出以前,人们普遍认为所有复杂网络均为随机网络,且其节点的度分布为泊松分布,而在无标度网络提出后,人们发现自然界中的大量网络(例如: 科研合作网络、蛋白质相互作用网络、因特网、社交网络等)都具有无标度特性,因此无标度网络的特性引起了许多研究人员的兴趣.无标度网络具有较强的异质性,各节点之间的连接具有较强的不均匀性,即网络中极少数的中心节点拥有极多的连接,而大多数节点只有很少量的连接.网络中的这些中心节点对网络的动力学和功能起着关键性作用.而无标度网络所具有的较强的异质性主要来源于其星型结构的模体.星型网络可以看成是无标度网络在统计意义下重整后的理想简化模型,但与无标度网络具有多个中心节点不同,星型网络只有一个中心节点,其网络结构更加简单,易于分析,因此可通过研究简单的星型网络的特性来帮助理解无标度网络的某些特性.

同步现象是指具有相互作用的系统之间形成的步调一致的运动.其中,在复杂网络中节点的同步是指网络中的各节点的动态行为具有一致性[12].同步现象广泛存在于自然界中,如在物理、生物、化学及社会系统中均可观察到,并具有较为丰富的应用,包括Josephson-Junction阵列[13]、半导体激光器阵列[14]、萤火虫的闪烁[15]、心脏起搏细胞[16]、帕金森疾病[17]和其他一些应用[18,19].耦合相振子模型(Kuramoto模型)[20−22]因能够简单且有效地描述很多物理系统中的同步和相变行为而成为研究同步问题的经典模型.本文拟以Kuramoto模型研究星型结构网络的同步优化问题.耦合Kuramoto模型中,每个节点代表一个具有不同自然频率的相振子,在解耦时以固定的自然频率做匀速旋转.节点之间通过相位影响产生耦合作用,星型网络上Kuramoto模型动力学方程如下:

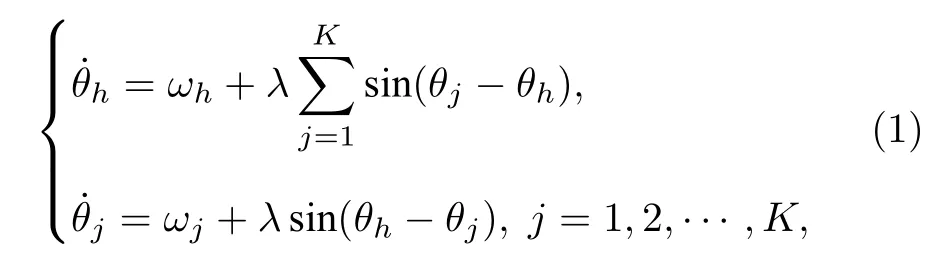
其中θh,θj分别表示中心节点和第j个叶子节点相位;ωh,ωj为对应的自然频率;λ为中心节点与叶子节点连接的耦合强度;K为叶子节点个数.当两个节点平均频率相等时,可认为它们达到同步.当耦合强度超过某一阈值时,耦合系统中所有节点的平均频率均相等并达到同步,我们称该阈值为同步临界耦合强度λc.同步优化就是通过调整或控制系统的参数使整个系统的同步临界耦合强度达到最小值,其与实际生活中的许多应用,例如电网的优化、通信领域、生物和医学等密切相关.

最近,星型网络上的同步有许多相关研究.Bergner等[23]在星型网络中发现了一种新的同步机制,即远程同步,具体表现为星型网络中的中心节点与叶子节点不同步的情况下,叶子节点之间可以实现同步.Schmidt等[24]研究发现在人类大脑神经网络中,中心节点对大脑模块之间的同步聚合发挥着关键性作用.这些对单个星型网络的研究让人们在纯星型网络上的同步方面有了更深的认识.而在无标度网络中,有多个中心节点并存且有可能存在相互作用,中心节点与叶子节点的异质性使得无标度网络的同步能力低于小世界网络[25].Zhang等[26]发现多层耦合网络中,可以很好地实现爆发式同步.通过引入星型网络模型,在无标度网络中引入与度相关的频率分布后,系统分析了实现爆发式同步和分层同步的产生机制[27].Xu等[28]分析了两个星型网络耦合情况下的同步相变问题.在上述星型网络的研究中,叶子节点的自然频率通常被设置成相等或是只存在较小的频率失配.然而,现实系统中这种理想假设条件常常无法达到,因而有必要讨论具有随机频率分布情形下,耦合系统的同步问题.

本文在叶子节点频率随机分布的情况下,讨论耦合星型网络的同步优化问题,以理论推导的同步临界耦合强度为基础,通过调节耦合系统的参数,获取最小同步临界耦合强度,从而实现对耦合系统的同步优化.第2节从单个星型结构网络着手分析同步优化问题,结果表明其同步临界耦合强度与中心振子频率之间具有分段线性关系,在分段点处取得最优值.第3节讨论两个星型结构网络相互耦合的情形,发现系统的同步临界耦合强度与两中心振子的频率之和间具有分段线性关系,且中心振子频率之和取在某一定值上时可使同步临界耦合强度达到最小值.当中心振子的频率不同时,系统具有不同的同步过程.当系统走向同步的过程中只有一个同步集团时,整个系统的同步临界耦合强度较小,而当系统中产生多个同步集团时,整个系统的同步临界耦合强度较大.第4节分析了多个星型结构网络耦合的情况,结果表明系统的同步临界耦合强度与所有中心振子的自然频率之和间存在分段线性关系.

2 单个星型网络

首先讨论单个星型网络的情况,网络结构如图1(a)所示.Wang等[29]研究并从理论上确定了单个星型网络的同步条件.当系统达到同步时,系统所有节点的平均频率都相等,设为W,(1)式可以转化为

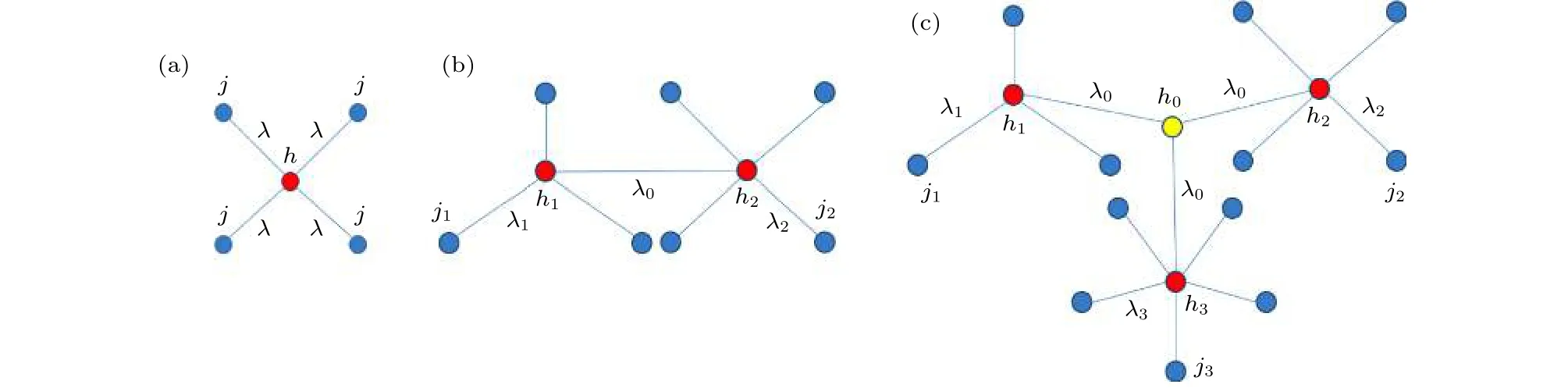
图1 耦合星型网络示意图 (a)单个星型网络; (b)两个耦合星型网络; (c)多个耦合星型网络Fig.1.Coupled star networks: (a) Single star network; (b) two coupled networks; (c) multiple coupled networks.

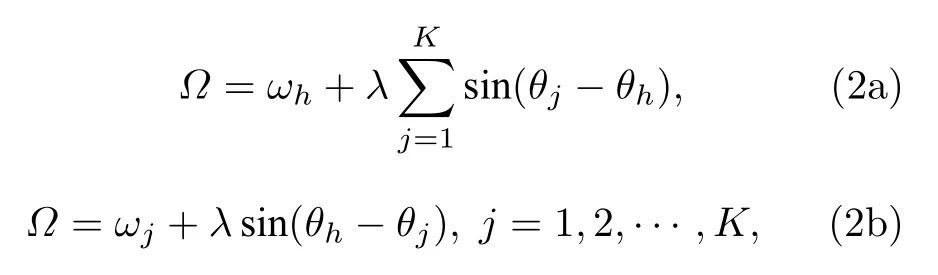
合并(2a)和(2b)式可以得到

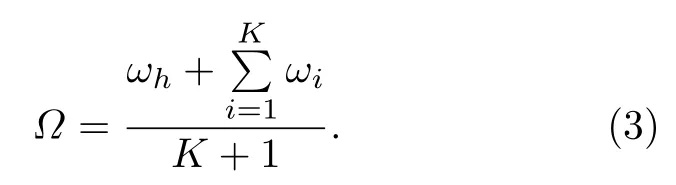
当系统同步时,叶子节点满足(2b)式,则

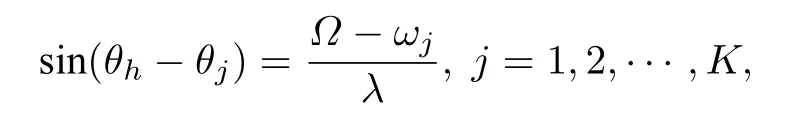
由于正弦函数的有界性得

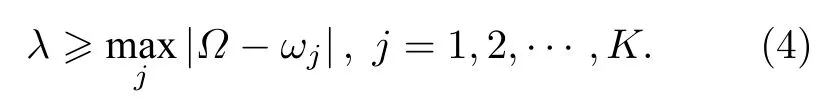
将(3)式代入(4)式得到临界耦合强度:

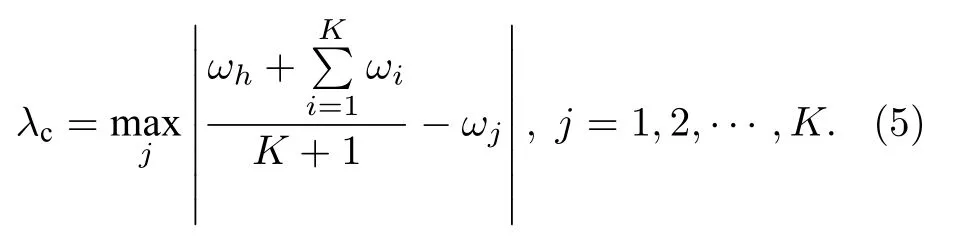
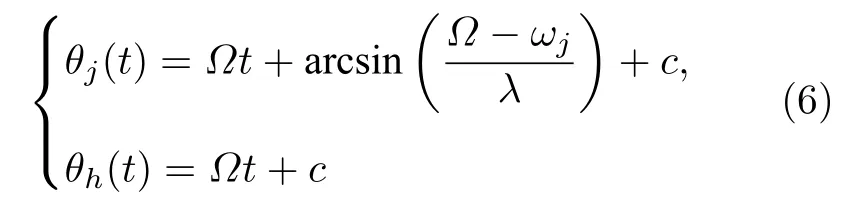
时,(1)式对应雅克比矩阵的特征值全部小于0.实际计算结果表明,λ≥λc时,对于任意的初始相位,耦合系统都会同步到(6)式的通解上.因此,λ≥λc时系统能达到同步,说明使用正弦函数的有界性得到的结果是可靠的.

从(4)和(5)式可知,临界耦合强度为所有节点的频率与最大(小)频率的差的平均值,即:

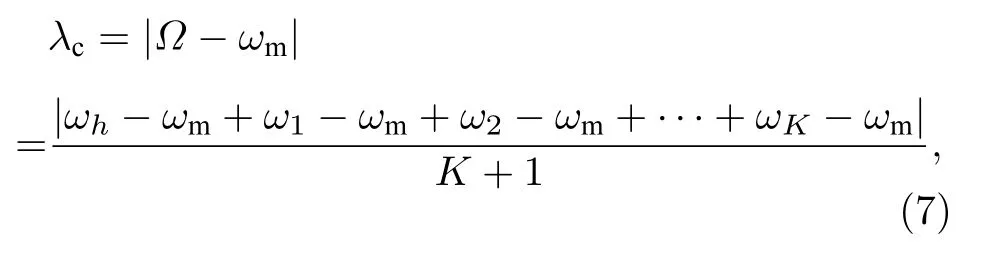
ωm为与平均频率差值最大的叶子节点的频率.由(4)式可知ωm与Ω差距越大,则所需的同步临界耦合强度越大.由(5)式可知,当节点频率变化时,同步临界耦合强度也相应地发生变化,相较于其他叶子节点,改变ωm对临界耦合强度的影响较大.λc=mjax|Ω−ωj|随着Ω的变化可以写成如下分段函数形式:

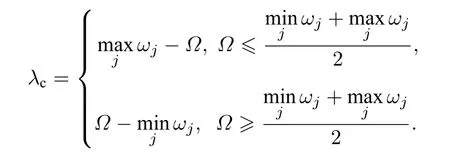
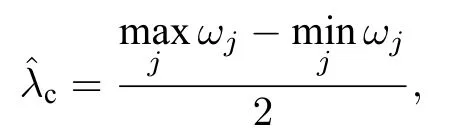
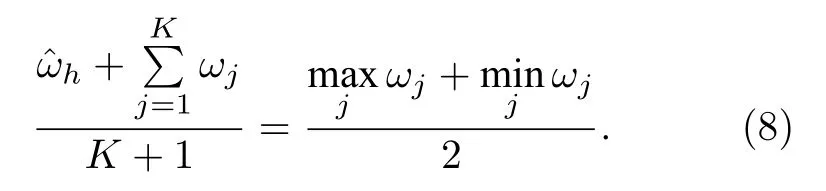
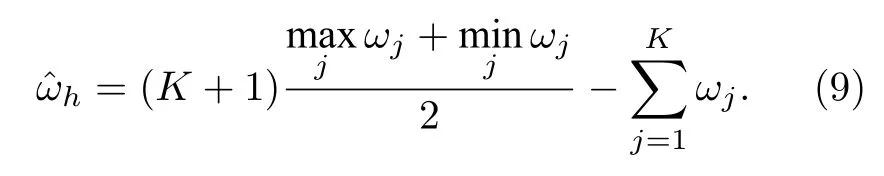
对于单个星型网络系统,由(7)式可知同步临界耦合强度与中心振子频率之间具有分段线性关系.当所有叶子节点频率确定时,由(9)式可得实现最优同步(最小同步临界耦合强度)对应的最优中心振子频率.即当整个系统的平均频率等于叶子节点频率最大值与最小值的中点时,星型网络系统的同步临界耦合强度有最小值.

3 两个相互耦合的星型网络

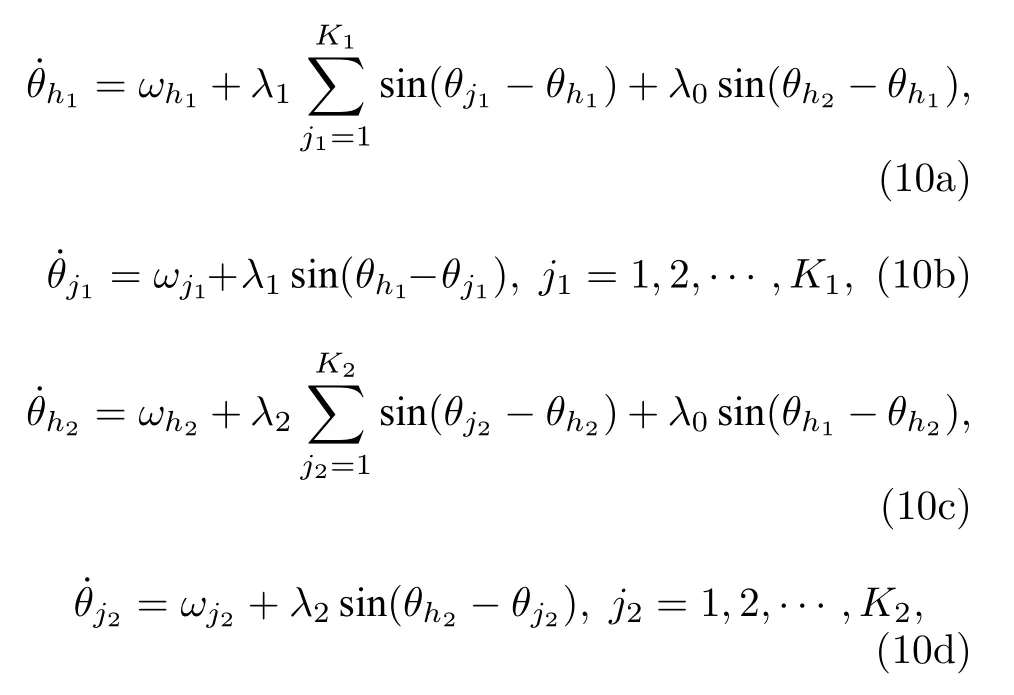
其中θh1,θh2,θj1,θj2和ωh1,ωh2,ωj1,ωj2分别是S1和S2的中心节点和叶子节点的相位、自然频率;K1,K2和λ1,λ2是S1和S2中叶子节点的数目、叶子节点和中心节点间的耦合强度;λ0是S1和S2中两个中心节点之间的耦合强度.

以K1=3,K2=4 为例,令耦合强度λ0=λ1=λ2=λ,基于四阶Runge-Kutta法计算(10)式,获得不同中心节点频率ωh1,ωh2下,节点的平均频率随耦合强度λ的变化,如图2(a)—(e)所示.对任意给定的ωh1,ωh2,都可以计算出对应的同步临界耦合强度λc.图2(f)给出了系统的同步临界耦合强度λc随ωh1,ωh2的变化关系.可知,同步临界耦合强度在不同的参数区域呈现不同的变化趋势.在远离对角线的左上和右下区域,同步临界耦合强度沿对角线方向基本不变,而在沿对角线的垂线方向发生改变.越接近对角线,同步临界耦合强度越小;在对角线附近区域,同步临界耦合强度在对角线的垂线方向基本不变,而在沿对角线方向发生变化,并在中间某处取得最小值.图2(a)—(e)给出了在图2(f)中的五个黑点对应参数下的平均频率随耦合强度变化关系.图2(a)和图2(e)是远离对角线的情形,随着耦合强度的增大,耦合系统的节点会先形成两个同步子集团,再通过两个同步子集团合并而达到同步.图2(b)—(d)是靠近对角线的情形,随着耦合强度的增大,耦合系统的节点会直接先形成一个规模较大同步集团并通过不断吸引其他节点加入而走向整体同步.与通过大集团与小个体竞争走向同步相比,两个规模相当的同步集团相互竞争走向同步的难度明显要大,因此要使系统更容易达到同步,应该尽量避免使系统产生多个同步子集团.

下面讨论耦合星型网络中,节点的频率值对系统同步临界耦合强度的影响.当系统达到同步时,所有节点的平均频率相等,可将(10)式合并并消去耦合项得到系统的同步平均频率为

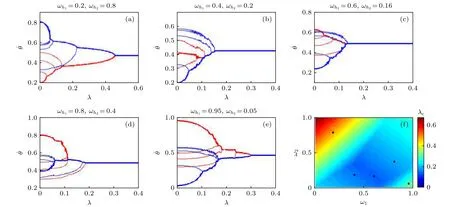
图2 ωj1=[0.31,0.42,0.5],ωj2=[0.58,0.53,0.57,0.33−]情况下的数值计算结果 (a)−(e)不同中心节点频率情况下的节点平均频率随耦合强度的变化,其中红线和蓝线分别表示(a)(e)不同中心节点频率情况下的节点平均频率随耦合强度的变化,其中红线和蓝线分别表示S1和S2的节点,粗线和细线分别表示中心节点和叶子节点; (f)系统临界耦合强度 λc 随 ωh1,ωh2 值的变化,越靠近冷色调表示临界耦合强度越小Fig.2.Numerical results for ωj1=[0.31,0.42,0.5],ωj2=[0.58,0.53,0.57,0.33].(a)−(e) Average frequency versus coupling strength for two coupled star networks S1 (red) and S2 (blue).The thick and thin lines respectively represent the center nodes and leaf nodes.(f) The critical coupling strength λc versus ωh1,ωh2.The value of λc is shown according to the colorbar.

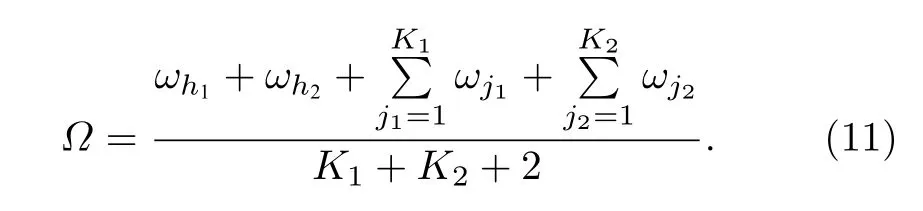
根据同步条件,(10b)和(10d)式中S1和S2的叶子节点满足:

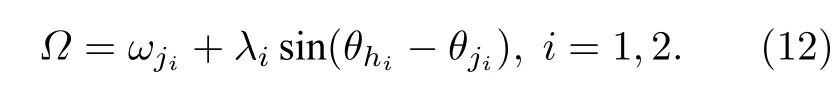
由正弦函数的有界性得

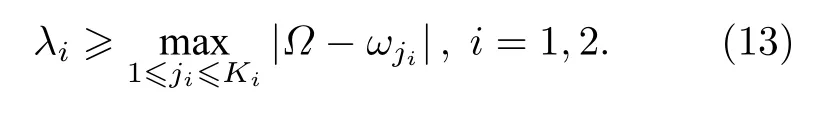
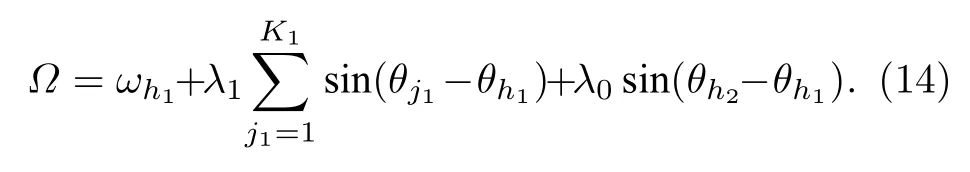
由(12)式可得

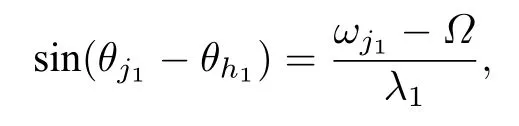
将其代入(14)式得

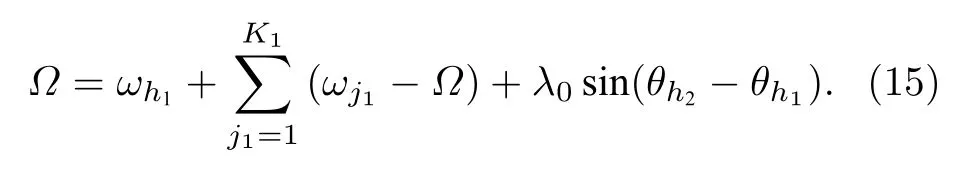
由正弦函数的有界性得

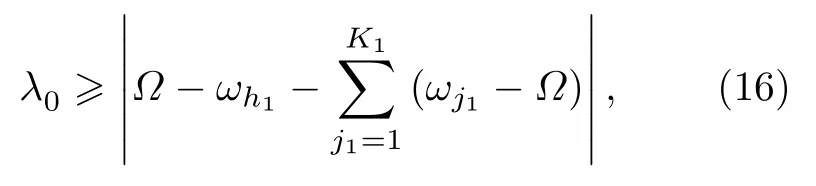
(16)式是通过S1的中心节点的(10a)式得到的,通过S2的中心节点的(10c)式同样可得以上结果.

令

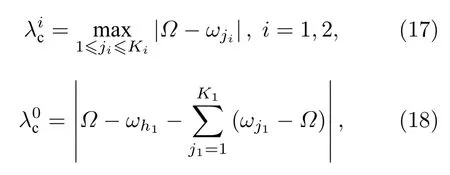
系统最优同步临界耦合强度处于图3(d)中的白线所在参数区域,此时随之和的变化情况如图4所示,临界耦合强度与中心振子频率之和满足分段线性关系,如(19)式,并在分段点处取得最小值.图中两条线的交点c处横坐标满足的线性关系为图3(d)中(1),(2)部分的分割线.在c点附近小于与,此时由或决定.在c点处,取合适的范围(图3(d)中为小于与,此时同步临界耦合强度具有最小值.下面理论导出最优的使同步临界耦合强度取最小值.

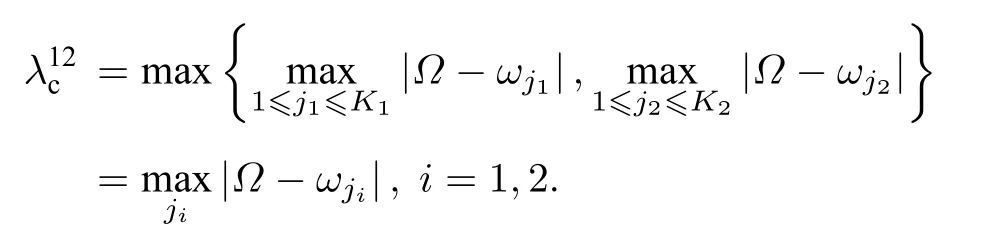
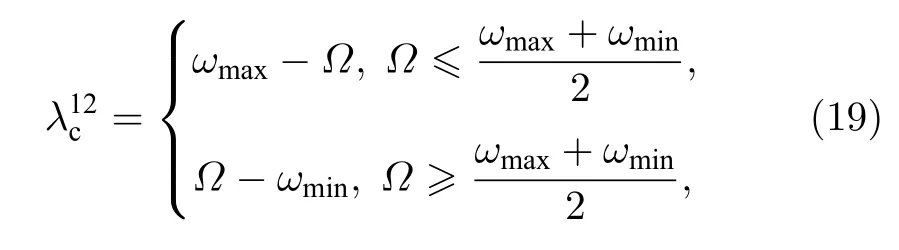
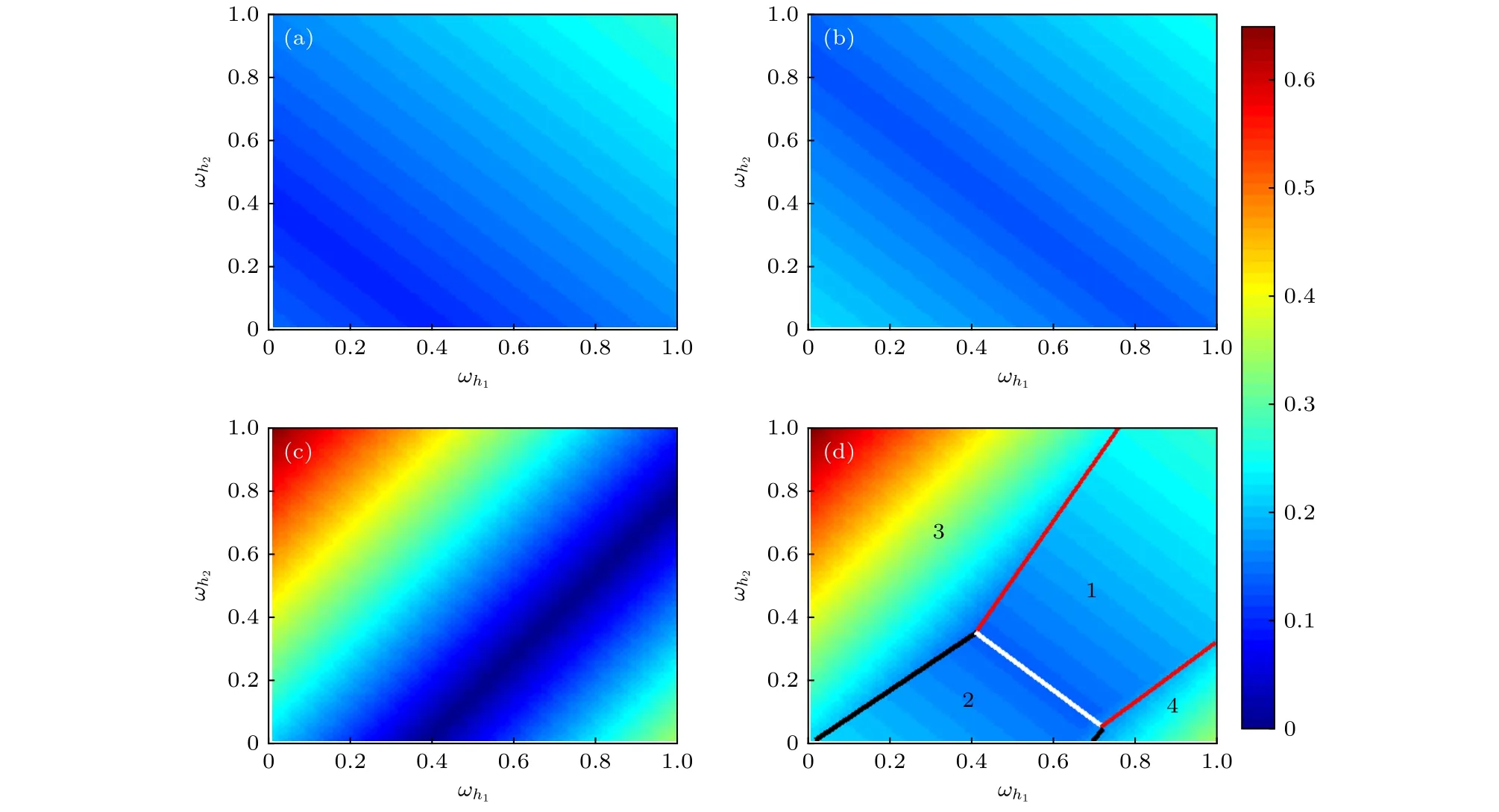
图3 (a)−(c)分别表示值的变化情况; (d) 随值的变化情况参数平面被分为不同的区域,两条红线表示与相等的区域,两条黑线表示与相等的区域,白线表示与相等的区域Fig.3.(a)−(c)versusversuswhere the parameter space can be divided into different regions according to the value of ; the red lines denotethe black lines denotethe white lines denote

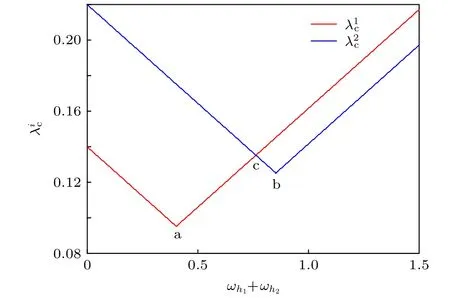
图4 系统的临界耦合强度随 ωh+ωh 值的变化情况12Fig.4.Relationship betweenand ωh+ωh.12

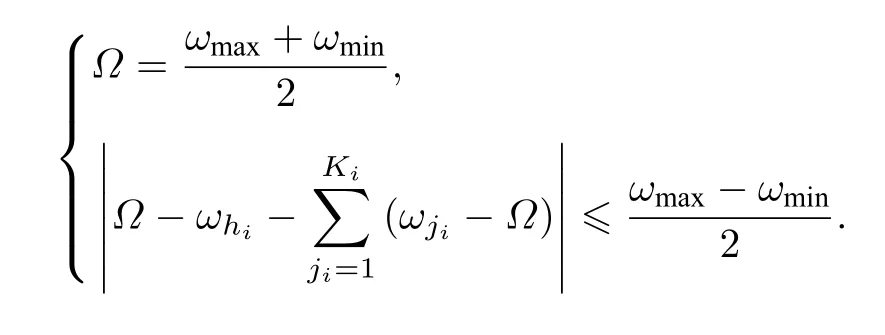
将(11)式Ω值代入上式可得耦合系统取得最优同步临界耦合强度λc的条件如下:

当λ0,λ1,λ2不相等时,分别固定λ0或者λ1,改变剩下的两个耦合强度得到系统的同步情况,对于每一组固定的耦合强度,计算系统稳定时节点的平均频率,进而得到这些节点平均频率的方差的对数值,如图5所示.只有当三个耦合强度均大于系统的同步临界耦合强度时,系统才能达到同步.数值计算结果如下: 图5(a)中当时,S1中的中心节点无法与S2中的中心节点同步,图5(a)中(1)部分中S1中上所有叶子节点和中心节点能同步,而S2的无法达到同步,图5(a)中(2)部分则与中的节点均各自无法同步,图5(a)中(3)部分的所有叶子节点和中心节点同步,的所有叶子节点和中心节点同步,但和未同步,图5(a)中(4)部分的所有叶子节点和中心节点同步,未同步.图5(b)与图5(a)类似,但此时和的中心节点同步,图5(b)中(3)部分中系统达到完全同步.图5(c)中数值结果发现始终不能同步,而在图5(d)中图5(d)中(3)部分时,系统达到完全同步.

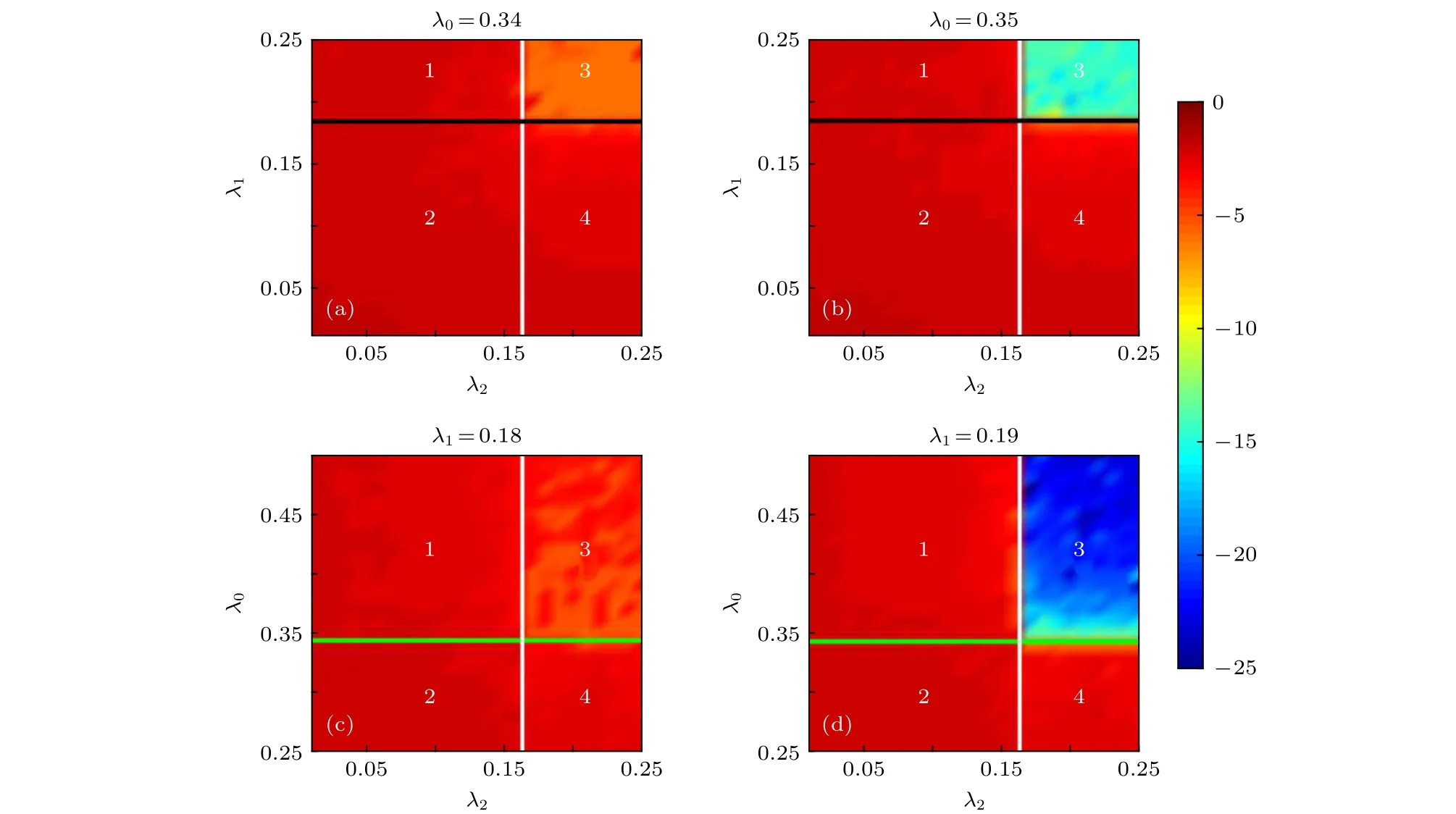
图5 ωh=0.4,ωh=0.8 时,不同耦合强度参数区间下,节点平均频率的方差的对数值 (a) λ0<; (b) λ0>;12(c) λ1<; (d) λ1>λ1c ,颜色越靠近冷色调表示系统的同步程度越高,黑线、白线、绿线分别表示理论推导出的,,Fig.5.Logarithmic variance of average frequency in parameter space of coupling strength for ωh1=0.4,ωh2=0.8 : (a) λ0<;(b) λ0>; (c) λ1<λ1 c ; (d) λ1>.The smaller logarithmic variance of average frequency indicates better synchronization.Black line,white line and green line represent the theoretical critical coupling strength for synchroniation ,,,respectively.

4 多个星型相互耦合网络

考虑n个星型网络耦合的情况,引入一个中心连接节点h0,n个星型网络的中心节点与节点h0相互耦合,将第i个星型网络称为Si,网络结构如图1(c)所示.该耦合系统的动力学方程为

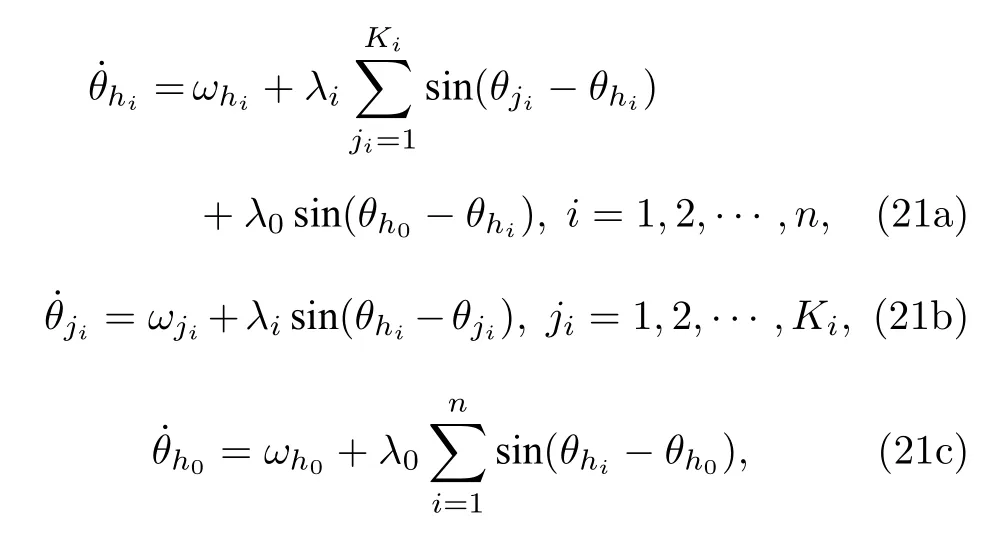
方程中的θhi,θji和ωhi,ωji是Si中的中心和叶子节点的相位、自然频率;Ki是Si中的叶子节点的个数;λ0是Si中的中心节点与中心连接节点h0间的耦合强度.当系统达到同步时,所有节点的平均频率

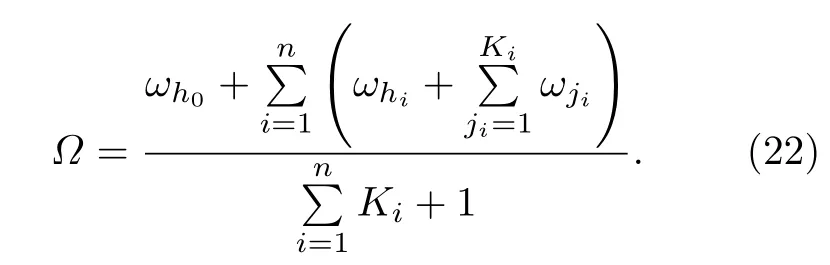
由(21b)式和同步条件可得

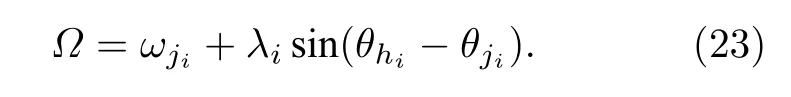
将(21a)和(21b)式合并得

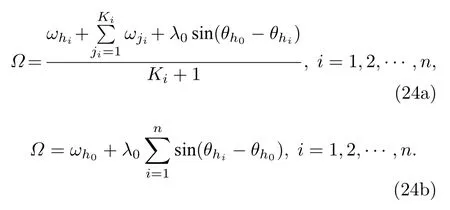
由(23)和(24a)式可得

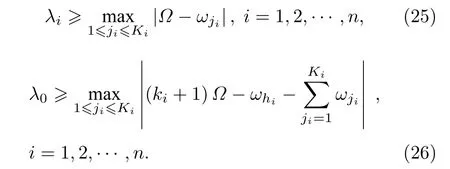
令

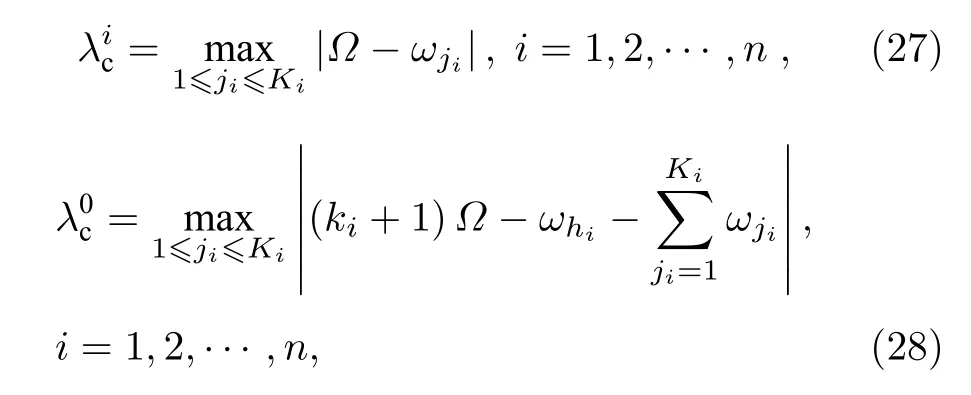
一定有解,即在ωhi的和为某一定值时,都可以找到一组ωhi使得=0.当取耦合强度相等即λ0=λ1=λ2=λ时,系统的同步临界耦{合强}度为(27)和(28)式的最大值,即λc=max,.以K1=3,K2=5,K3=4为例,对于所有不同的可得到使=0 的ωhi,并以此振子频率为参数通过数值计算获得系统的同步临界耦合强度,如图6(a)中的圆圈所示,此结果与理论推导的结果一致,如图6(a)所示.

固定λ1=0.41≥,λ2=0.5≥,改变λ3,λ0时,计算所有节点平均频率的方差的对数,如图6(b)所示,其中绿线和白线分别是由理论得到的,.结果表明理论推导的同步临界耦合强度与数值计算结果一致.图6(b)中(1)部分λ0>,λ3>,所有中心节点与连接节点同步,S3未同步; (2)部分λ0>,λ3>,中心节点未与连接节点同步,S3未同步; (3)部分所有λ0>,λ3>,系统完全同步; (4)部分≥,≥,S3的所有叶子节点和中心节点同步,各中心节点未同步.同样地,对于不同的Ki,理论结果与数值计算结果依然符合.

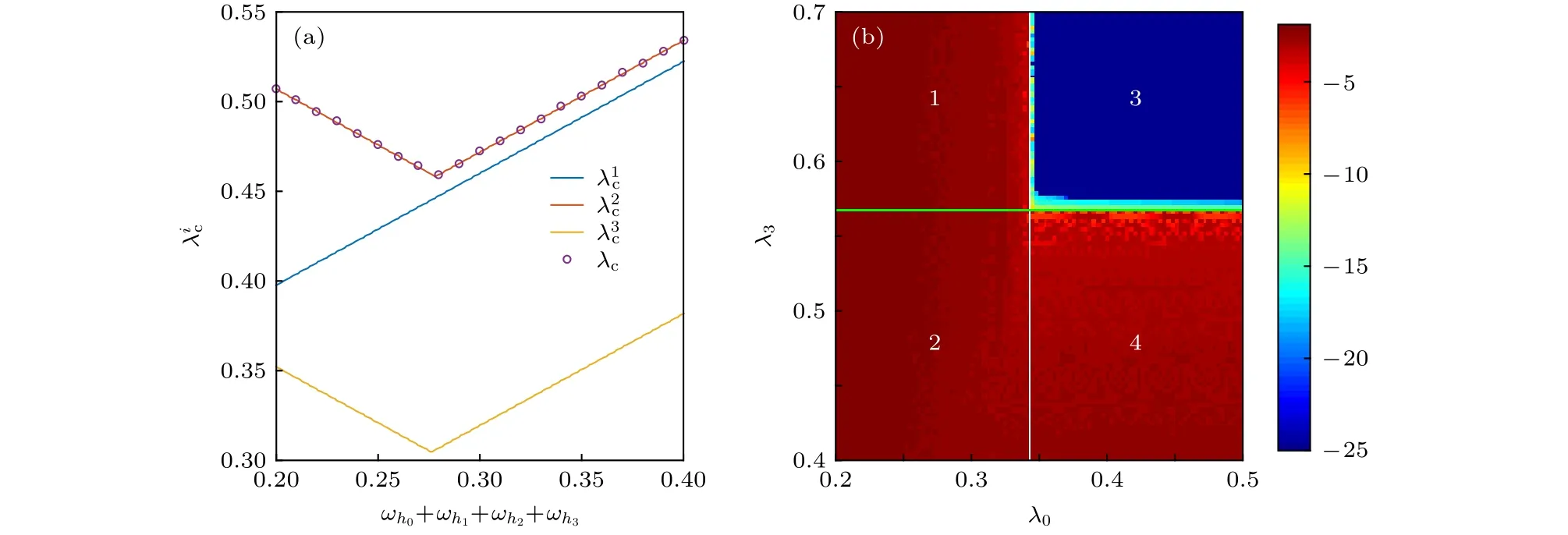
图6 参数为ωj1=[0.27,0.05,0.10],ωj2=[0.69,0.31,0.84,0.95,0.03],ωj3=[0.77,0.80,0.19,0.49]时的数值计算结果(a)控制所有耦合强度相等时,系统的同步临界耦合强度随 ωhi 的和的关系图,数值计算结果如圆圈所示,理论推导结果如实线所示; (b)当固定 λ1=0.41,λ2=0.5 ,改变参数 λ3,λ0 时,所有节点平均频率的方差的对数结果,绿线和白线分别是理论得到的,Fig.6.Numerical results and theoretical results for ωj1=[0.27,0.05,0.10],ωj2=[0.69,0.31,0.84,0.95,0.03],ωj3=[0.77,0.80,0.19,0.49]: (a) The critical coupling strength for synchronization versus the summation of central node frequencies; the numerical results are shown in the circle and the theoretical ones are shown in the solid lines; (b) the logarithmic variance of average frequency in parameter space of λ3,λ0 for given λ1=0.41,λ2=0.5.

5 结 论

本文讨论了具有非全同叶子节点的多个耦合星型网络的同步优化问题.单个星型网络节点频率对系统同步临界耦合强度的影响结果表明,同步临界耦合强度与中心节点的频率满足分段线性关系,在分段点处具有使同步临界耦合强度达到最优的频率.

两个耦合星型网络中,理论导出了每个子星型网络内部实现同步所需的临界耦合强度,以及两个星型网络之间实现同步所需的临界耦合强度.当系统所有耦合强度相同时,系统的同步临界耦合强度λc=max{,,} ,改变两个中心节点的自然频率会影响同步临界耦合强度,的值,从而影响系统的同步临界耦合强度λc的值.在最优点附近同步临界耦合强度与两个中心节点自然频率之和满足分段线性关系.中心节点的自然频率的参数平面会分成不同的区域,在每一个区域内临界耦合强度由相应的或者决定.在由决定的区域里:≥,≥,两个星型网络先各自内部实现同步而形成两个同步子集团,最后系统达到同步所需的同步临界耦合强度较大.在由决定的区域里:≥,≥,随着耦合强度的增大,只会产生一个同步集团,子网络S1中叶子逐渐加入到同步集团,系统达到同步所需的临界耦合强度较小.由决定的区域里的情况与决定的区域的情况一样,在这两个区域相交的部分:=≥,随着耦合强度的增大,系统先产生一个同步集团,然后不断有叶子节点并入到同步集团,直到两个子网络S1,S2的所有叶子并入同步集团,系统达到完全同步,系统的同步临界耦合强度最小,此时两个中心节点自然频率的和为一固定值.当各子网络间的耦合强度不相等时,当且仅当各子网络的耦合强度均大于等于相应的同步临界耦合强度,时,系统才能达到同步.如果某一部分不满足条件,该部分对应的节点就不能同步.

多个耦合星型网络中,通过理论推导得出了每个子星型网络内部同步的临界耦合强度,以及子星型网络之间同步的临界耦合强度.当系统所有耦合{强度相}同时,系统的临界耦合强度λc=max,.当中心连接节点和中心节点的频率之和为任意定值时,调节中心连接节点和中心节点的频率可以使较小,系统临界耦合强度λc由决定,此时λc与中心连接节点和中心节点的频率和成分段线性关系,在分段点处取得最小值.在最优的情况下,随着耦合强度的增大,只会产生一个同步集团.

总之,随着耦合强度的增大,当系统产生多个同步集团时,临界耦合强度较大,而只产生一个同步集团时临界耦合强度较小,因此为了优化同步应该尽量避免产生多个同步集团,而应该是只有一个大集团不断吸收小个体的方式.