球形和卧式pVTt标准容器中气体流场非稳态数值模拟

朱洺征　刘若璇　沈昱明

摘  要： 使用FLUENT软件，以流体力学N-S方程和能量方程为基础，引入理想气体状态方程，并考虑浮升力影响，通过建立数学模型，采用CFD方法，对容积为5 m3的pVTt气体流量标准装置中包括球型和卧式二种形状的标准容器，在等温壁面条件下抽气、进气，以及自然對流过程进行了数值模拟，分别得到了二种容器中空气的流速、压力和温度云图。模拟结果显示，在相同条件下，球型容器进气后产生的温差较小，但是温度均匀时间与卧式容器相当;二种容器中的空气压力均能很快稳定。

关键词： 传感器;pVTt;标准容器;等温边界条件;数值模拟

中图分类号： TP319    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.07.038

【Abstract】： Based on FLUENT software， Using N-S equation and energy equation of fluid mechanics as well as the ideal gas state equation， and after consideration of the influence of buoyancy lift， numerical simulation of the pumping， intake， and natural convection processes under isothermal conditions in the pVTt gas flow standard facility with a volume of 5 m3 （including standard containers in spherical and horizontal shapes） was conducted by establishing the three-dimensional model and using the CFD method. The flow velocity， pressure and temperature clouds of the air in the two containers were obtained respectively. The simulation results show that under the same conditions， the temperature difference generated by the spherical container after intake is relatively small， but the temperature uniform time is equivalent to that of the horizontal container; and the air pressures of both containers stabilize fast.

【Key words】： Sensor; pVTt; Standard container; Isothermal boundary condition; Numerical simulation

0  引言

pVTt法气体流量标准装置是应用非常广泛的一种原始级气体流量标准装置。在抽气和进气结束后，pVTt容器内的气体温度和压力需要经历一段较长时间的自然对流过程，最终达到容器内温度和压力基本均匀和稳定。通过测量，得到容器内的均匀后的气体平均温度和平均压力，最后根据理想气体状态方程算出容器中的气体质量。

目前，pVTt法气体流量标准装置多以卧式容器作为装置的标准容器，气体介质也常为空气。实验和数值模拟结果表明，无论在抽气和进气过程后，温度达到基本均匀且稳定需要花费几十分钟甚至更长时间[6]，从而降低了装置的使用效率。为此，国内外学者开展了针对pVTt法气体流量标准装置的大量的研究工作。文献[1]指出pVTt法气体流量标准装置的计量准确度不仅受温度传感器性能影响，与测温点的布置方案有明显关系，并给出了温度传感器的布置方案;文献[2]讨论了由于不均匀的室内空气条件而产生的空气温度梯度带来的容器中空气温度的不确定性;文献[3]介绍了NIST大流量pVTt法装置，装置采用水浴恒温的温度场稳定方案;文献[4-5]讨论了采用包括风机恒温、水浴恒温条件下，pVTt法气体流量标准装置进气过程与均匀过程中，容器内气体温度场的时变特性;文献[6]针对等温和绝热二种边界条件，对标准容器气体的速度、压力和温度分布进行了数值模拟。从以上文献可以看到，pVTt装置中的标准容器均为卧式结构。

本文在文献[6]的基础上，调整了计算模型，分别对容积为5 m3的卧式和球型二种结构的pVTt标准容器在等温壁面边界条件下，气体进气过程进行了非稳态流场的数值模拟。得到了容器中空气的速度、温度和压力分布云图。在相同条件下，球型容器进气后产生的温差较小，但是温度均匀时间与卧式容器相当;二种容器中的空气压力均能很快稳定。

1  控制方程与建模

1.1  控制方程

假定空气为可压缩粘性完全气体，且考虑浮升力影响，则粘性可压缩流体非定常流动的连续性方程、N-S方程组和能量方程分别为[7]

1.2  建模与网格划分

运用CFD软件，分别对5 m3的卧式和球形二种容器建立简化几何模型，其中卧式容器直径为1.1935 m，长4.497 m;球体容器半径为2.5231 m。为了获得更精确的计算结果，强调壁面温度和浮升力的影响，运用ICEM CFD 17.0软件，对模型进行了非结构化的网格划分，在容器壁面处进行网格加密，并建立8层边界层，逐层加厚。二个容器的网格划分数量均约为500万个，最小角度≥30°，网格总体质量大于0.5，负网格个数为0。卧式和球形容器模型与网格划分图如图1所示。

为了计算空气质量，在卧式容器沿容器轴向方向均匀截取3个界面，在每个截面上沿直径方向均匀布置3个测温点，一共9个测温点，如图1所示。

1.3  边界条件

根据控制方程，并加入无滑移边界条件。设置容器内初始条件：空气温度为300 K，压力为101.325 kpa，抽气结束时的压力为0.5×101.325 kpa;进气过程的初始条件即为抽气结束时的状态参数。当容器中压力达到0.8×101.325 kpa，进气过程结束。等温边界条件，设壁面温度为293.15 K。

2  数值模拟与分析

在等温壁面边界条件下，分别对5 m3的卧式和球形二种形状的pVTt标准容器，在抽气和进气过程进行数值模拟实验。模拟实验中，分别观察二种容器在抽（进）气开始和结束时的温度和压力分布及其平均值。抽（进）气结束，即判断容器内的温度、压力达到均匀的判断条件是容器内温差<0.1 K，压差<10 pa。

2.1  卧式pVTt标准容器数值模拟

仿真实验开始首先对容器进行抽气，抽气结束后，模拟实验发现，二种容器内的温差均超过了10 K，压差超过0.7 kpa。经过约200 s时间的自然对流，容器内的温度和压力均达到均匀状态。限于篇幅，抽气过程不作赘述。

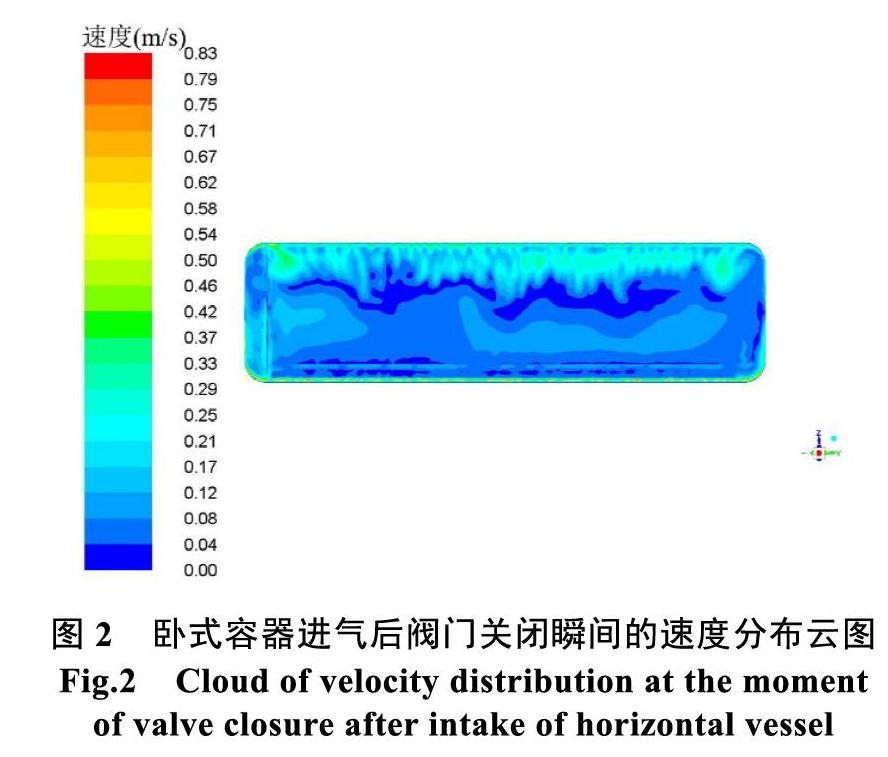
然后阀门打开，容器开始进气。本文详细讨论容器的进气过程。图2给出了卧式容器进气（阀门关闭）后瞬间的速度分布云图;图3分别给出了卧式容器进气（阀门关闭）后瞬间和经过自然对流以后的温度分布云图;图4为卧式容器压力均匀后的压力分布云图。

2.2  球形pVTt标准容器数值模拟

在相同初始条件和边界条件下，对5 m3球形容器也作了抽气和进气的数值模拟。限于篇幅，这里也只讨论进气过程。图5为球形容器进气（阀门   关闭）后瞬间的速度分布云图;图6分别给出了球形容器进气（阀门关闭）后瞬间和经过一段时间的自然对流后的温度分布云图;图7为稳定后的压力分布云图。

2.3  模拟结果分析

从图2、5可以可到，进气后，二种容器内的流

速分布是紊乱的，流速范围约为0～0.30 m/s之间，流速较大的区域在容器的上半部分。

图3为卧式容器的温度分布云图。从图3（a）可以看到，进气结束（阀门关闭）后，容器内的空气温差可以达到15 K，温度较高的区域仍集中在容器的上部。经过约300 s时间自然对流以后，温度逐渐趋于均匀，容器中部区域温度略高于其它区域。

从图6（a）可以看到，进气后，球形容器内的空气温差约为5 K左右，远小于卧式容器。与卧式容器不同，球形容器进气后，在球的中心大部分区域空气温度较高，且较均匀。完全均匀以后（偏差<0.1K，下同），与卧式容器相似，球形容器仍然保持球体中部区域温度略高的分布状态。

图4和图7是二种形状容器当压力基本均匀以后（偏差<10 pa，下同）的压力分布云图。分布云图相似，在入口区域，压力略低。

图8给出了二种容器平均压力随时间的变化趋势。从图中可以看到，无论是卧式容器还是球形容器，容器内空气压力均在35s时间内达到均匀。

图9给出了二种容器平均温度随时间的变化趋势。而对于温度而言，平均温度达到均匀的时间则相对比较缓慢。从图8可知，卧式容器在经过300s之后，空气温度达到均匀，而对于球形容器，经过100s左右的自然对流，空气温度即达到均匀。

3  结论

本文在以往工作的基础上，调整了计算模型，强调壁面温度和浮升力的影响。建模时，在容器壁面处建立了8层边界层，逐层加厚。模拟实验显示，这样的网格加密处理能很好反映容器中气流的流场分布情况。经过数值模拟，得到以下结论：

图9  平均温度变化趋势

Fig.9  Trends in average temperature

（1）在相同条件下，无论是抽气还是进气过程，卧式和球形二种结构的pVTt标准容器内的空气压力均能很快达到均匀（偏差<10 pa）。对于实验中的5 m3容器而言，二种结构的容器压力稳定时间均约为35 s，呈现出了明显的梯度分布。

（2）对于温度而言，球型容器比卧式容器产生的温度不均匀性较小，但温度均匀速度与卧式容器相当，均约为300 s。

参考文献：

徐志鹏， 洪育仙， 樊奇， 谢代梁. 多传感器pVTt法气体流量标准装置测温方案研究[J]. 传感技术学报， 2015， 28（5）： 635-640.

Johnson A N， Wright J D， Moldover M R， et al. Temperature characterization in the collection tank of the NIST 26m3 pVTt gas flow standard[J]. Metrologia， 2003， 40： 211-216.

Wright J D， Johnson A N， Moldover M R， et al. Gas Flowmeter

Calibration with the 34Land 677L pVTt Standards[J]. NIST Spe?cial Publication， 2003， （7）： 13-64.

白瑞琴. pVTt法氣体流量标准装置关键技术的研究[D]. 杭州： 中国计量学院， 2012.

白瑞琴， 程佳， 李东升等. 水浴恒温式pVTt法气体流量标准装置温度场仿真研究[J]. 传感器与微系统， 2011， 30（12）： 43-46.

Zhao Xuening， Luo Dong， and Shen Yuming： The calculation method of pVTt standard temperature and pressure vessel simu?lation under two kinds of boundary conditions[J]， IMEKO Inter?national Seminar on Measurement 4-5 Sep， 2017， Hangzhou， China.

赵学瑞， 廖其奠. 粘性流体力学[M]. 北京： 机械工业出版社， 1983.

王连杰， 韦群. 三维云图仿真系统设计与实现[J]. 软件， 2018， 39（5）： 151-155.

王佳美， 周志尊， 胡明成， 等. 颅脑动脉瘤模型构建与计算流体力学分析[J]. 软件， 2018， 39（5）： 70-74.

张学烨， 周欢娣. 基于三维仿真技术的数据实时过程管理在精度造船中的应用研究[J]. 软件， 2012， 33（11）： 129-131.

周力， 杨建辉， 侯有良. 基于ansys的搅拌臂和搅拌叶片的仿真分析[J]. 软件， 2012， 33（10）： 91-92.