最长递增子序列问题研究

乔明泽　宋传鸣

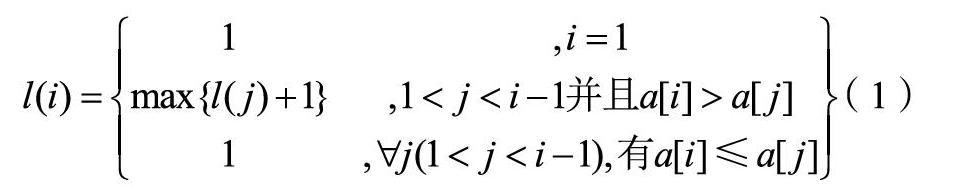
摘  要： 本文采用分治策略和动态规划策略探讨了最长递增子序列问题的两种解法，并分析了算法的计算复杂度。结果表明，本文算法的时间复杂度和空间复杂度分别为O（nlogn）和O（n）。

关键词： 最长递增子序列;分治;动态规划;算法

中图分类号： TP391    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.07.005

本文著录格式：乔明泽，宋传鸣. 最长递增子序列问题研究[J]. 软件，2019，40（7）：3134

【Abstract】： By employing the divide-and-conquer and dynamic programming strategies， this paper discusses two algorithms of the longest increasing subsequence problem. The computational complexity of two algorithms was subsequently analyzed. The analysis results show that the time complexity and spatial complexity of two proposed algorithms achieve O（nlogn） and O（n）， respectively.

【Key words】： Longest increasing subsequence; Divide-and-conquer; Dynamic programming; Algorithm

0  引言

最长递增子序列（Longest Increasing Subsequence， LIS）问题是计算机算法学、随机矩阵理论、表示理论、组合数学和生物信息学领域的典型问题之一[1]，其问题描述如下：设L是一个有n个元素的序列 。若L存在某子序列    满足   ，则称l是L的一个递增子序列，并称m为递增子序列l的长度。最长递增子序列问题就是要求序列L的一个长度最长的递增子序列。

目前，最长递增子序列问题已经被广泛研究。文献[2，3]分别给出了该问题的动态规划解法;文献[1]首先将LIS问题转化为最长公共子序列问题，再利用动态规划算法求解;文献[4]则将LIS问题转化为图的最长路径问题进行动态规划求解。上述算法的计算时间复杂度均为O（n2）。在总结和分析现有算法不足之后，文献[1]利用数组链表和二分查找改进了典型动态规划算法中的查找操作，从而将算法的時间复杂度降低到O（nlogn），但是其辅助空间较大，且算法较为复杂。另外，国内尚鲜见关于最长递增子序列问题的详细实现过程且其时间复杂度达到O（nlogn）的研究资料。

本文利用分治策略和动态规划策略[5]设计了两种最长递增子序列问题的O（nlogn）复杂度算法。分治解法的基本思路是将长度为n的序列分解为长度较短的子序列，再递归求解这些子序列的LIS，最后将各个子序列的解合并成原序列的解;动态规划解法的基本思路与分治法类似，不同之处在于前者用一个数组来记录那些已解决的子问题的答案，从而避免重复子问题的计算，降低时间复杂度。

本文内容安排如下：第1节讨论最长递增子序列问题的分治解法;第2节首先证明最长递增子序列问题具有最优子结构性质，然后详细论述其动态规划解法;第3节总结全文。

1  最长递增子序列的分治解法

分治是一种简单、直接的算法设计策略，其基本思想是将一个规模为n的问题分解为k个规模较小的、互相独立的子问题且与原问题相同。递归计算每个子问题，然后将各个子问题的解合并为原问题的解[5]。依据此思想，下面讨论本文的求解思路。

1.1  LIS问题分治解法的主要思路

首先，将序列L大致平均分成左、右两个子序列L1和L2，递归求这两个子序列的最长递增子序列。

其次，以L1的最长递增子序列为基础向L2序列扩展，得到一个递增子序列a。

再次，以L2的最长递增子序列为基础向L1序列扩展，得到一个递增子序列b。

最后，序列L的最长递增子序列即为a、b中的较长者。

对于L1和L2的最长递增子序列求解，由于其形式与原问题完全相同，解法与L的最长递增子序列解法一致。故此，为了保证分治算法具有较低的时间复杂度，关键环节是如何高效地将L1和L2的解合并为L的解。

1.2  子问题解的合并

将原序列 划分成两个相互独立的子序列， 、   ，然后递归求得BL和BR的最长递增子序列bl和br，然后将bl和br扩展为L的最长递增子序列sub。

显然，这里划分的两个子序列BL和BR没有重叠部分，是相互独立的，即具有子问题不重叠性质。对于子问题解的合并，给出下列合并思路。

1： bl←new int[（last-first）/2+1]

2： br←new int[（last-first）/2+1]

3： l ←LIS_DC（first，mid，bl）

4： r ←LIS_DC（mid，last，br）

//以左子数组的最长递增子序列为基础，向右子数组扩展，得到一个递增子序列

5： for i←0 to l

6： sub[i]←bl[i]

7： end for

8： i←l-1 ，  p←i+1 ，  sub[p]←MAX

9：  for k←mid to last      //向右扩展的区域[mid，last）

10：    if sub[i]

11：    ++i ，  p←i+1 ，  sub[p]←a[k]

12：    else if sub[i]a[k] && sub[i]

13：    sub[p]←a[k]

14： else if sub[i]a[k] && sub[i]>a[k] && sub[i-1]

15：    sub[i]←a[k] ，  sub[p]←MAX

16：  end if

17：  end for

18：  if sub[p]=MAX then

19：  --p

//以右子數组的最长递增子序列为基础，向左子数组扩展，得到一个递增子序列

20：  subr←new int[（last-first）/2+1]

21：  j←0，  subr[j]←br[0]，  q←j+1，  subr[q]←-MAX

22：  for k←mid-1 to first  //向左扩展的区域[first，mid）

23：     if subr[j]>subr[q] && subr[q]>a[k] then

24：    ++j ，  q←j+1 ，  subr[q]←a[k]

25：     else if subr[j]>subr[q]&&subr[q]a[k]

26：         subr[q]←a[k]

27：     end if

28：  end for

29：  if subr[q]= -MAX then

30：  --q

//合并，数组sub即为求得的L的最长递增子序列

31：  if p+1>=q+r then

32：  s←p+1

33：  else s←q+r

34：  for k←q to 0

35：     sub[i++]←subr[k]

36： for k←0 to r

37：     sub[i++]←br[k]

1.3  LIS问题的分治解法步骤

根据上文的分析，下面给出本文提出的LIS问题的分治解法步骤。

算法输入：数组a，数组sub，起始下标first和终止下标last

算法输出：最长递增子序列及其长度

算法LIS_DC （a，sub，first，last）

1：   if last-first=2 then    //递归结束的基准条件

2：   if a[first]>a[first+1] then

3：      sub[0]←a[first+1]，  return 1

4：   else

5：      sub[0]←a[first]，  sub[1]←a[first+1]，  return 2

6： end if

7： else if last-first=1 then

8：   sub[0]←a[first]，  return 1

9： end if

10： mid←（first+last）/2

11： l←LIS_DC（first，mid，bl）

12： r←LIS_DC（mid，last，br）

1.4   计算复杂度分析

由于采用了二分法递归且递归函数中只存在一层循环，所以该算法的时间复杂度T（n）=O（nlogn）。

每次递归，当前函数都大致开辟i+2个sizeof（int）空间 ，所以总共大致开辟了2（n-1）+2logn个sizeof（int）空间，即空间复杂度S（n）=O（n）。

2  最长递增子序列的动态规划解法

动态规划是求解具有最优子结构性质的最优化问题的有效算法设计策略之一，其基本思想是将规模为n的问题分解成若干个子问题，这些子问题往往不是互相独立的、而是重叠的，且满足最优子结构;每求解出一个子问题，就将其答案保存到数组中，从而避免重叠子问题的多次计算;最后以自底向上的方式从子问题的解得到原问题的解[5]。

2.1  最长递增子序列问题具有最优子结构性质

定理1 设序列L的最长递增子序列为    （1

证明  假设b不是subL在 条件下的最长递增子序列，则存在另一个subL的递增子序列  1i，   ，那么可以構造 ，因为j>i，所以l2子序列的长度大于l1子序列的长度，l2才是L的最长递增子序列。这与l1是L的最长递增子序列相矛盾。因此，假设不成立，即b是 subL在 条件下的最长递增子序列。证毕。

由上述定理可知，最长递增子序列问题具有最优子结构性质。

2.2  一般解法

依据最优子结构性质，可以得到最长递增子序列问题的解的递归表达式为：

（1）

由此即可获得下文的最长递增子序列问题的动态规划解法。

每个数据元素采用的数据结构为：

struct node

{

DataType data; //结点的值

int pre; //结点的前序

unsigned int count; //以该结点为结尾的递增子序列的长度

};

算法输入：保存在node a[M]数组中的n个元素

算法输出：最长递增子序列及其长度

算法LIS_DM1 （a）

0：    初始化数组a，t←0

1：    for i←1 to n

2：      max←0

3：      for j←0 to i-1

4：      if a[j].data

5：          max←a[j].count， k←j   //max记录着a[0，..，i-1]中count最大的值;

//k记录着max对应a[0，..，i-1]的下标;

6：      end if

7：     end for

8：     if max=0 then

9：       goto 1

10：     end if

11：     a[i].count←max+1， a[i].pre←k

12：     if a[i].count>t then

13：   t=a[i].count   //t记录a[0，…，n-1]中count最大的值

14：     end if

15：   end for

16：   for i←0 to n

17：     if a[i].count=t then

18：   output 以a[i]结尾的最长递增子序列

19：     end if

20：   end for

2.3  基于二分查找和链栈的动态规划解法

由公式⑴和算法LIS_DM1可知，计算每个l（i）时都需要寻找满足 条件的最大的l（j）。由于是l（j）无序的，顺序查找需耗费O（n）的时间复杂度。若能利用特殊的数据结构实现有序的l（j），即可用二分查找方法完成最大l（j） 的搜索，从而将时间复杂度从O（n）降低到O（logn）。基于这种思路，本文设计了一种基于二分查找和链栈的动态规划解法。

每个数据元素采用的数据结构为：

struct Element

{

DataType d;     //结点的值

Element* pre;   //d的前续坐标，即在上一层链表中某节点

Element* next;

};

Element  *s;      //s作栈

int Top=0;  //栈顶 栈中元素在s[0，Top）中

算法输入：保存在node a[M]数组中的n个元素

算法输出：最长递增子序列及其长度

算法LIS_DM2（a）

0：  初始化栈s，栈顶Top←0

1：  for i←0 to n-1

2：    s[i].q←NULL

3：  end for

4：  for i←0 to n-1

5：    l←0，mm←Top，h←Top，flag←false

6：    do while l<=h

7：       m←（l+h）/2

8：       if s[m].q=NULL then   //s[m].q指向的鏈表无元素

9：          break

10：      end if

11：      if s[m].q→d>a[i] then    //s[m].qt→d是s[m].q链表中的最小元素

12：        mm←m，h←m-1      //mm保存着最近一次s[m].q→d>a[i] 时m的值

13：      else if s[m].q→d

14：         l←m+1

15：      else

16：         flag←true，break

17：      end if

18：   end do

19：   if flag=true

20：     goto Step 7

21：   end if

22：   将a[i]加入到s[mm].q指向的链表中

23：  end for

24：  rprint（s[Top-1].q）;  //输出最长递增子序列

2.4  计算复杂度分析

一般解法中，LIS_DM1算法的计算量主要集中在二重循环阶段，其时间复杂度为T（n）=O（n2）;另外，上述算法采用了1个包含n个元素的一维数组，故其空间复杂度为S（n）=O（n）。

改进动态规划解法，相对于上述的一般解法而言，在内层循环中采用二分查找法，这样时间复杂度就从O（n2）降到O（nlogn）。但是需要多消耗些空间用于保存数据，LIS_DM2算法运用栈和链表辅助存储，栈中元素有序，所以能使用二分查找，提高效率。具体分析如下。

因为s[0].q→d，s[1].q→d，s[2].q→d，s[3].q→d，...，s[Top-2].q→d，s[Top-1].q→d是递增有序的，所以可以采用二分查找法查找mm，使得s[0].q→d，s[1].q→d，s[2].q→d，s[3].q→d，...，s[mm-2].q→d，s[mm-1].q→d都小于a[i]，而从s[mm].q→d开始到s[Top-1].q→d都大于a[i]。这样a[i]用头插法添加到s[mm].q指向的链表中。

故其时间复杂度为T（n）=O（nlogn），空间复杂度为S（n）=O（n）。

3  结束语

最长递增子序列问题是计算机算法设计与分析中的典型问题，在数学、物理等学科中亦有广泛应用。本文采用分治和动态规划策略设计了两种最长递增子序列求解算法，并给出了详细的实现步骤，其时间复杂度均为O（nlogn），空间复杂度为O（n）。

参考文献

[1] 严华云， 李刚， 张建宏. 生物信息挖掘中LIS算法研究[J].计算机应用研究， 2009， 26（1）： 62-63， 6.

[2] SKIENA Steven S. The algorithm design manual[M]. 第2版 北京：清华大学出版社， 2009.

[3] 《编程之美》小组. 编程之美——微软技术面试心得[M]. 北京： 电子工业出版社， 2012： 194-198.

[4] DASGUPTA S.， PAPADIMITRIOU C.， VAZIRANI U..算法概论[M]. 钱枫， 邹恒明， 译. 北京： 机械工作出版社， 2012： 157-159.

[5] 王晓东.计算机算法设计与分析[M]. 第4版. 北京： 电子工业出版社， 2012.