一种快速构建点云坐标系的方法

文/李宇洁 卿都

由于获取点云数据的传感器的快速发展，点云数据变得越来越多，而且也越来越容易获取。点云是物体在三维空间中的一种表达方式[1]，这些点与二维图像中的平面像素点不同，是空间中的立体像素点，因此这些点是离散的、独立的。如今，在计算机可视化中，点云三维模型已经越来越受到人们的欢迎，并逐渐成为视觉、机器人、医学、遥感、虚拟现实和增强现实[2]等领域的核心工具。如机器人需要进行物体抓取时，需要首先获取物体在某个坐标系中位置与姿态，因此构建物体的自身坐标系是非常重要的。构建物体的自身坐标系最简单的方法就是手动标注，根据物体的形状确定物体坐标系的原点，以及X、Y、Z轴的方向。文献[3]中使用统一机器人描述格式(URDF)方法，以世界坐标系为基坐标系，给出旋转向量和平移向量确定物体自身的坐标系。文献[4]使用一种海明码的格子图作为视觉标志，把这个标志贴在物体上，然后使用摄像头检测视觉标志的位置，通过Levenberg-Marquardt算法[5]求得贴在物体上的标志在相机坐标系中的位姿，并且可在物体表面构建一个坐标系。

前面介绍的方法需要人为参与，或者需要辅助标志，不能快速、稳定地构建物体自身的坐标系。本文提出了使用物体点云的三维模型，求得点云的形心坐标、以及三个主成分方向，从而确定物体的坐标系。

1 三维空间主成分分析

通过实验观察发现，三维点云在空间中的整体分布具有一定的规律，一个物体的三维点云整体上能表现出这个物体的外形和轮廓，因此这些点云在X轴、Y轴、Z轴上具有一定的相关性。借鉴PCA(Principal Component Analysis)[6]主成分分析的思想，求取数据分布的主成分方向，并且每一个主成分之间是相互垂直的。PCA能实现从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个坐标轴是数据分布中方差最大的方向，第二个坐标轴是与第一个坐标轴垂直且在该方向上的方差最大，第三个轴与第一、第二个轴组成的平面相互垂直，并且第三个轴所指的方向是方差最大的方向。三维空间主成分分析示意图,如图1所示，u、v、w分别是在方差从大到小的方向向量。

2 坐标系构建方法

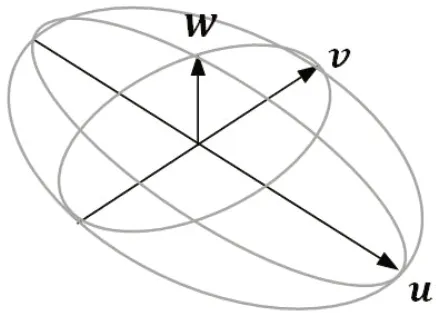
图1：三维空间主成分分析示意图

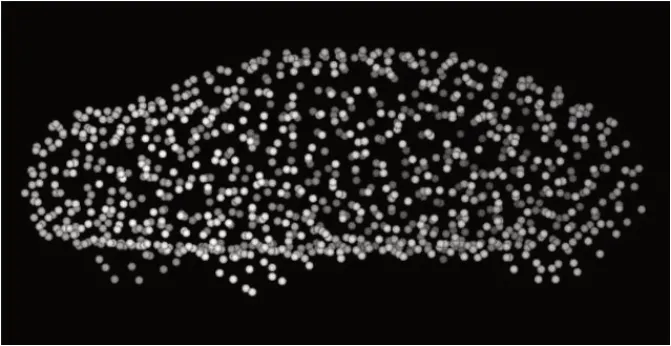
图2：小车点云图

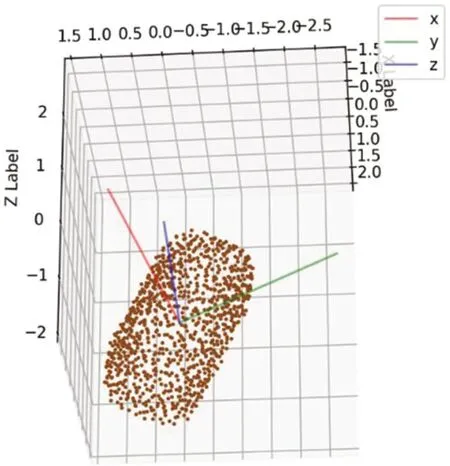
图3：小车坐标系

点云是物体在三维空间表现的一种方法，这些点不再是二维图像中的平面像素点，而是空间中的立体像素点，因此这些点是离散的、独立的，如图2所示是一辆玩具小车的点云图。为了便于描述点云物体相对于世界坐标系的位姿，故需要求得该物体的三维几何中心，即物体的形心，以及描述物体姿态的坐标系。

已知点云集合中有N个点，k为某个点云X= (X,Y,Z)T∈R3的邻域中包含点的个数，k∈N，k个点云代表一个物体的点云集合。pi=(xi,yi,zi)，pi∈N,点云的形心坐标o=(o0,oy,oz,)。形心坐标o可由（1）式求得。

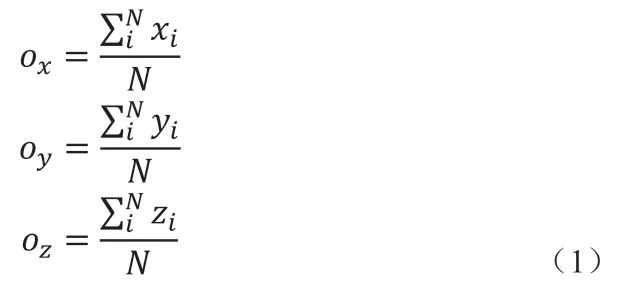
为了能够描述点云X的局部三维结构，需要求出k个点在X,Y,Z坐标值的协方差，如式(2)所示，可求得cov(X,X)，cov(X,Y)，cov(X,Z)，cov(Y,Y),cov(Y,Z),cov(Z,Z)，其 中cov(Y,Z)= cov(Z,Y)。

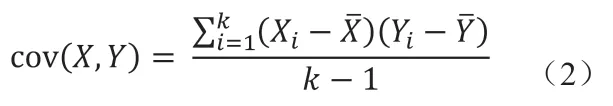
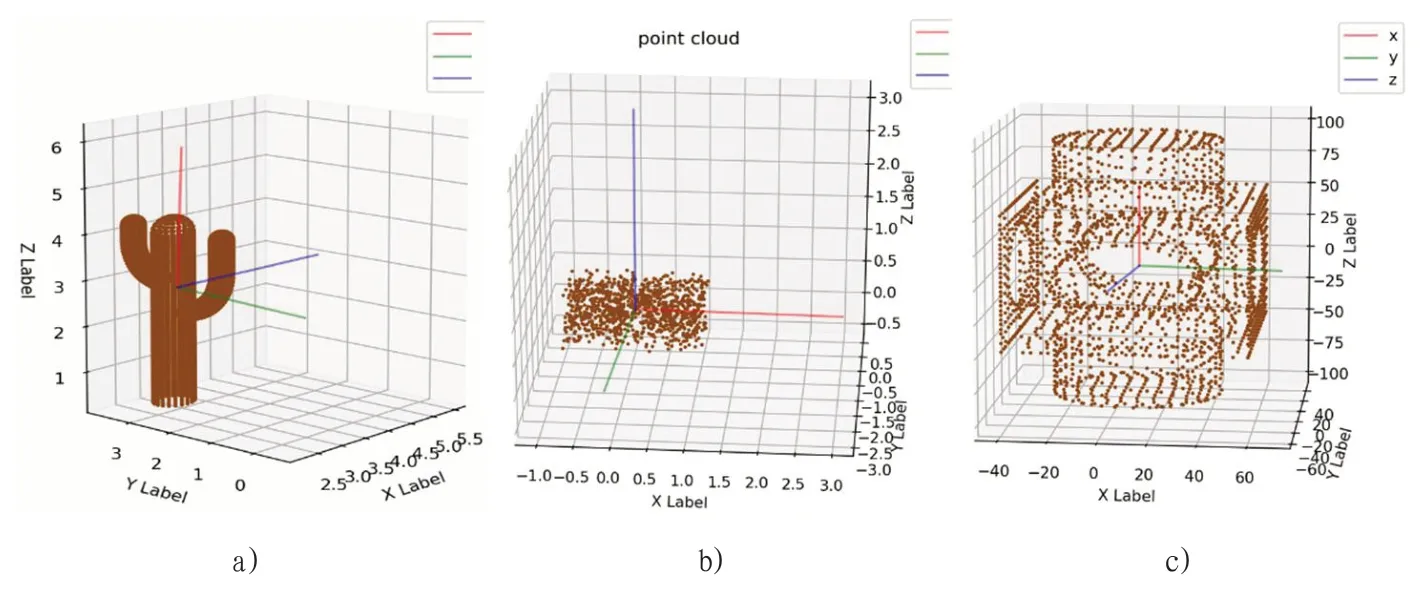
图4：点云物体坐标系

然后得到一个协方差矩阵S∈R3×3,如式（3）所示。

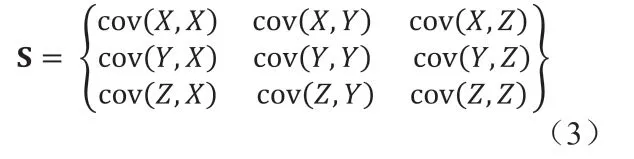
因为式（3）是一个对称正定矩阵，故由对称正定矩阵的性质得到该矩阵的三个特征值都是大于零的，即λ1≥λ2≥λ3≥0，对应的特征向量为V1、V2、V3。由式(1)可以求得点云的形心坐标o=(ox,oy,oz,)，点o作为表达物体自身坐标系的原点，特征向量为V1、V2、V3分别是物体自身坐标系的方向向量，由此可确定物体自身坐标系的原点以及坐标轴方向。如图3所示是图2中小车点云根据以上方法求得的坐标系。

3 实验结果

通过本文提出的点云坐标系构建方法，可以求得点云物体的形心坐标，以及坐标系中坐标轴的方向，如图4所示。红绿蓝分别表示X、Y、Z三个坐标轴，图4a)为仙人掌形状的物体，竖直方向为X轴。图4b)是一个立方体的点云物体，每一个坐标轴都垂直某一个物体表面的切平面。图4c)是一个空心的点云物体，求得的坐标系能很好的反应该物体的姿态。

4 结论

为了快速、稳定地构建物体自身的坐标系，本文提出了利用主成分分析方法确定坐标轴方向的方法。根据实验可知，同一个物体不管在任何时候或则任何姿态，求得的坐标系都是相对不变的，能够很稳定地反应物体在世界坐标系中的姿态情况。该方法实现的算法运行速度与物体点云个数是线性关系，即时间复杂度为Ο(n)。

该方法还有需要改进的地方，如需要前期获得物体的点云形式，当点云数量过大就会影响算法的运算速度。解决点云数量大的方法就是对点云进行下采样，减少点云数量，从而加快运算速度。