TWINE 算法的相关密钥不可能飞来去器攻击

谢敏，田峰，李嘉琪

（西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西 西安 710071）

1 引言

随着电子信息技术的迅猛发展，物联网、射频识别等技术被广泛应用，这使适用于资源受限设备的轻量级分组密码迅速成为研究热点。与传统分组密码相比，轻量级分组密码具有占用资源少、功耗低、效率高和易于实现等优势。从早期的HIGHT[1]、PRESENT[2]和MIBS[3]，到后来的LBlock[4]、PRINCE[5]和 Piccolo[6]等多种算法的提出，轻量级分组密码设计和分析的发展已经愈显成熟。

TWINE 分组密码算法是Suzaki 等[7]在Selected Areas in Cryptography 2012 上提出的一种轻量级分组密码算法，可以在计算资源受限的硬件和微型控制器上实现。TWINE 分组密码算法的设计采用了广义Feistel 结构，分组长度为64 bit，密钥长度分为80 bit 和128 bit 这2 种版本。算法的提出者对TWINE 进行了安全性分析，提出了15 轮的不可能差分路径，完成了对23 轮TWINE-80 和24 轮TWINE-128 的不可能差分分析；Zheng 等[8]对Suzaki 等在分析中关于计算复杂度上存在的一些漏洞进行了更正与补充，提出了更严谨的不可能差分分析；此后Wang 等[9]利用零相关线性分析的方法，对23 轮的TWINE 进行了分析，结论较已有分析有所改进；Coban 等[10]和Mohamed 等[11]对36 轮的TWINE 分别进行了Biclique 分析和中间相遇攻击，但其计算复杂度都接近穷举搜索；2017 年，Wei 等[12]对TWINE 进行了相关密钥不可能差分分析，并提出了TWINE 的等价算法，该算法描述简洁直观，更加有利于分析，他们构造了一条15 轮的相关密钥不可能区分器，并向上扩展4 轮，向下扩展5 轮，首次对24 轮的TWINE 进行了攻击，但在构造文章所述的明文对时，结构数n最大只能取到16，这会导致能恢复的密钥比特很少且无实际价值。

相关密钥不可能飞来去器[13]是近年来提出的一种新的分析方法，它结合了3 种不同分析方法的优势，对于轻量级的分组密码算法如LBlock 等已有较好的分析结果[14]。对TWINE 而言，引入相关密钥和飞来去器的方法可以使路径的选择变得更加灵活，本文采用相关密钥不可能差分飞来去器的方法对23 轮TWINE-80 算法进行了攻击，获得了较优的分析结果。

2 TWINE 分组密码介绍

2.1 TWINE 加密算法

TWINE 算法的分组长度为64 bit，密钥长度分为80 bit 和128 bit 这2 种，明文经过36 轮迭代得到密文。其中，轮函数采用了广义 Feistel结构，如图1 所示，结构中的S 盒如表1 所示。

图1 TWINE 算法的轮函数

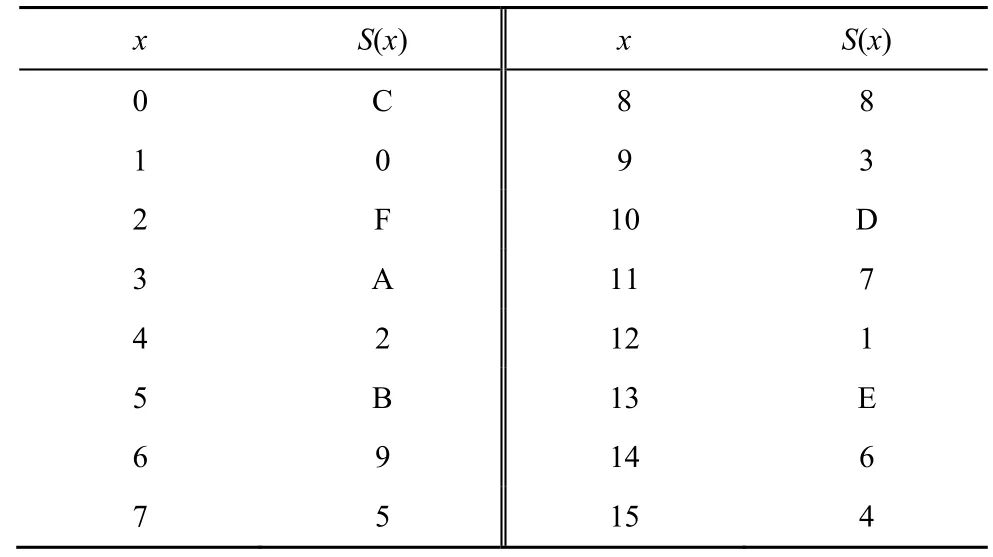
表1 TWINE 的S 盒

2.2 TWINE 的等价算法

Wei 等[12]将 TWINE 算法描述为等价的TWINE*算法，并对2 种算法的等价性进行了证明。TWINE*算法更加直观地体现了TWINE 算法的结构特点，便于更好地展开分析。本文将在TWINE*算法的基础上进行相关密钥不可能飞来去器分析，算法的描述如下。

1)第一轮进行置换IP，如表2 所示，置换后的明文分为左32 bit 和右32 bit。

2)按图2 所示加密结构进行迭代计算，其中P1和P2置换如表3 和表4 所示。

3)对最后一轮的轮函数输出进行置换FP，如表5所示。

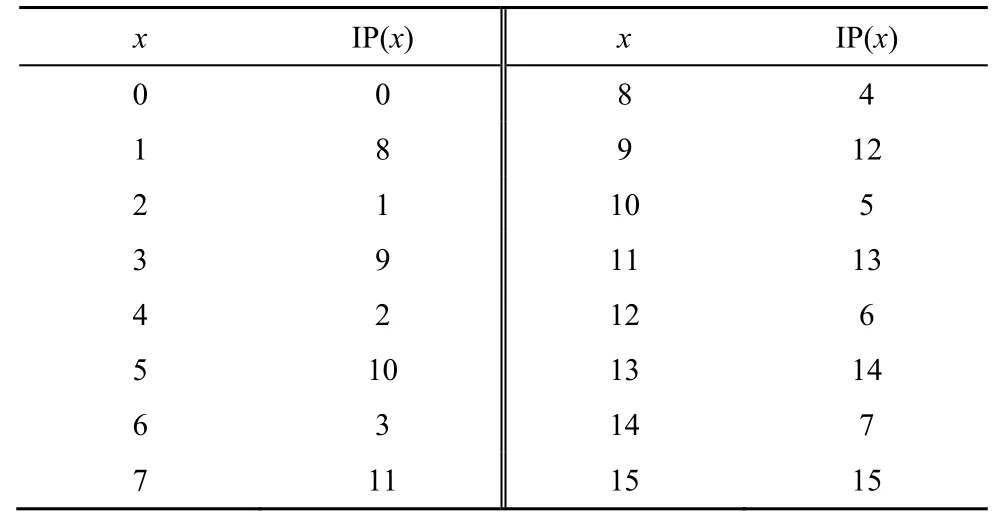
表2 置换IP

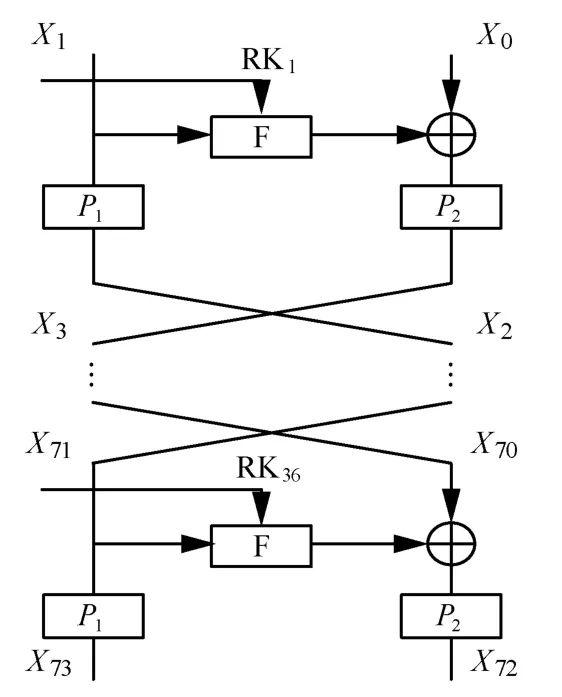
图2 TWINE*的加密结构

表3 P1置换

表4 P2置换

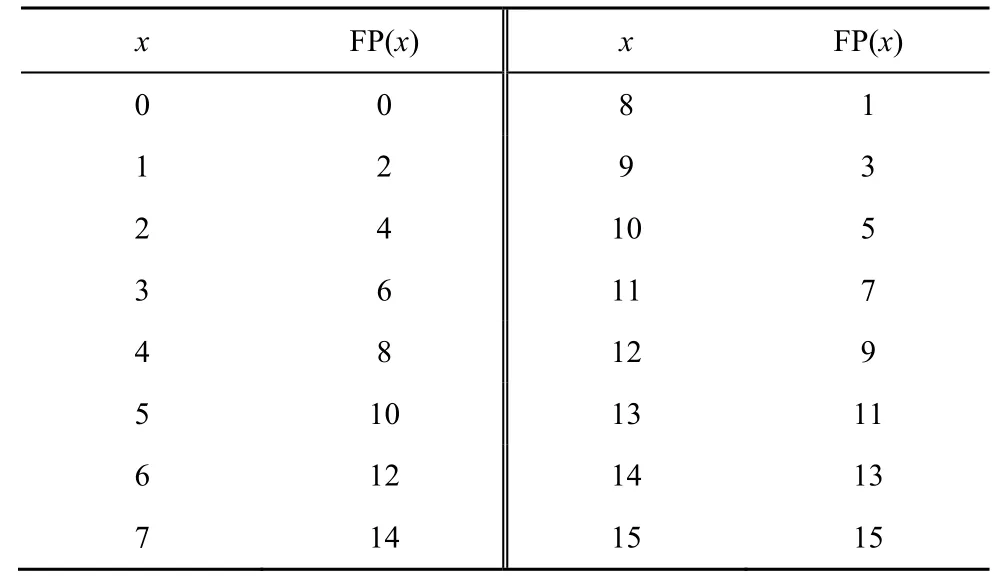
表5 置换FP

2.3 TWINE-80 的密钥编排算法

TWINE-80 算法的密钥编排算法为

其中，K为80 bit 主密钥，WKi(0≤i≤1 9)为半字节块。forr←1 to 35

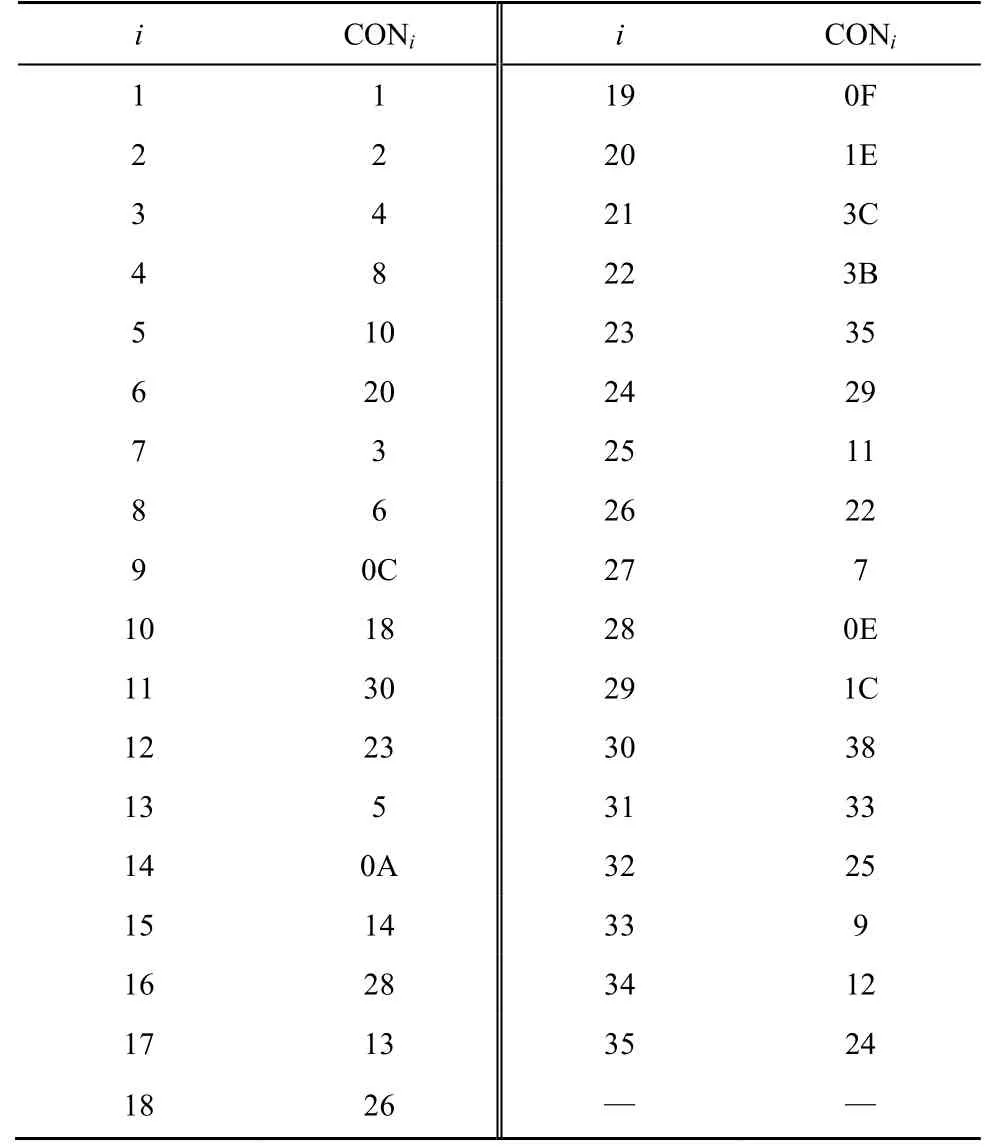
表6 CONi的值

3 相关密钥不可能飞来去器攻击介绍

相关密钥[15]、不可能差分[16]和飞来去器[17]都是被广泛应用的分组密码攻击方法，其中相关密钥利用了密钥编排算法的弱点，构造特定的密钥差分影响算法的加解密，从而构造路径恢复密钥；不可能差分攻击是用一条概率为0 的差分路径来淘汰符合这条路径的错误密钥；飞来去器则灵活地应用差分的特点将算法分为两部分进行分析，以寻找更好的路径。近年来，很多研究者倾向于将多种分析方法相结合，以期对算法安全性做出更好的研究[18-20]。

相关密钥不可能飞来去器攻击结合了以上3 种分析方法的思想。利用飞来去器和相关密钥的方法，可以在算法上下两部分做不同的密钥差分，有助于扩展攻击轮数；利用不可能差分，配合相关密钥对算法分析给出更多的可能途径，以便寻找到更好的分析路径。相关密钥不可能飞来去器的攻击方法如图3 所示。

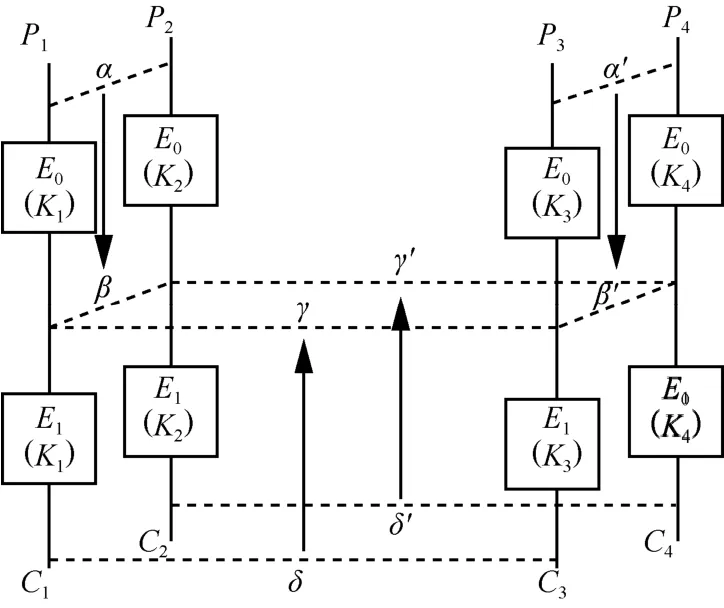
图3 相关密钥不可能飞来去器的攻击方法

算法分析过程中，加密算法E被分为2 种算法（E0和E1）的组合。P1、P2、P3、P4经对应密钥K1、K2、K3、K4加密分别得到(C1、C2、C3、C4)，其中4 个密钥满足K1⊕K2=K3⊕K4=ΔK1，并且K1⊕K3=K2⊕K4=ΔK2。图 3 中α、β、γ、δ、α′、β′、γ′、δ′均代表差分，α→β和α′→β′是E0中2 条概率为1 的差分路径，δ→γ和δ′→γ′是中2 条概率为1 的差分路径。在中间轮相遇时，β、β′、γ、γ′满足β⊕β′⊕γ⊕γ′≠ 0。

4 TWINE-80 的相关密钥不可能飞来去器攻击

4.1 路径构造

根据2.2 节TWINE 算法的等价算法TWINE*的描述，利用相关密钥不可能飞来去器的分析方法，构造出一个由16 轮和17 轮2 条路径组成的相关密钥不可能飞来去器区分器。并将其向上扩展4 轮，向下将2 条差分路径分别扩展3 轮和2 轮，完成了对23 轮TWINE 算法的分析。除特别声明外，下文符号“*”表示非零差分，“？”表示不确定的差分。

通过对TWINE 密钥编排算法的研究，发现对于每轮的密钥更新算法，有2 个半字节的主密钥会进入S 盒并参与异或运算，从而实现非零密钥差分的快速扩散。在相关密钥不可能飞来去器的构造中，选择区分器上半部分主密钥的特定半字节差分 WKi0 Δ≠，其中WKi在差分路径α→β、α′β′→ 中不会进入S盒，这样可以使非零差分的扩散变慢，同时区分器的长度增加。经过分析对比，并同时考虑到密钥恢复算法的计算复杂度，本文在本次攻击中选取了主密钥差分ΔWK=00000000000000020000，即ΔWK15=2，由此决定的轮密钥差分如表7 所示。

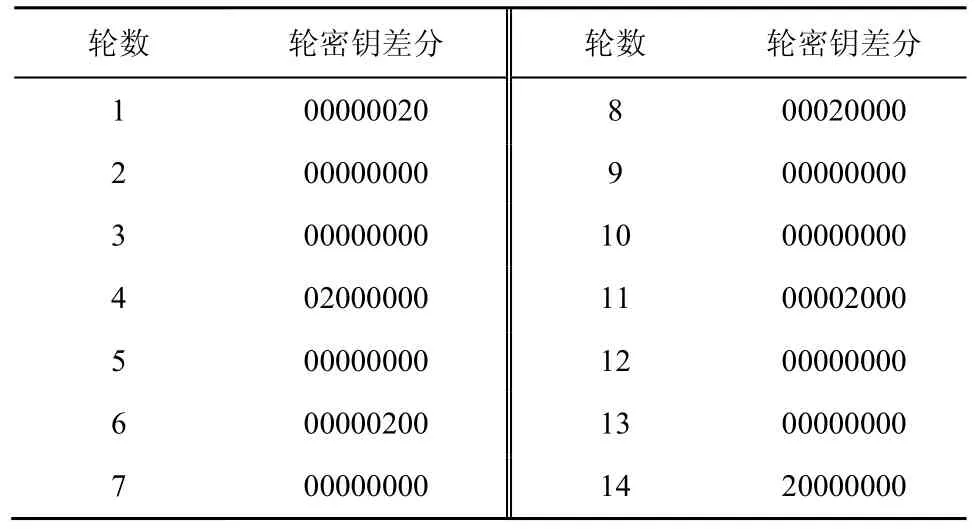
表7 轮密钥差分

由主密钥差分可推知，第6 轮、第7 轮和第8轮的轮密钥差分分别为00000200、00000000 和00020000（如表7 所示），若令第5 轮的输入差分为（00000000，00000020），经过两轮加密之后，第8 轮的输入差分为（00020000，00000000），易知这种构造可使得区分器的活跃S 盒数目大大降低，从而可以获得更长轮数的路径。因此，选取第5 轮的输入差分α和α′均为（00000000，00000020）。在区分器的下半部分，本文选择2 条不同的差分路径，结合不可能差分分析的思想，经过大量分析对比后确定了输出差分：一条差分路径中，选取第 20 轮的输出差分δ为（00000200，00000000）；另一条差分路径中，选取第21 轮的输出差分δ′为（20000000，00000000）。在此基础上根据相关密钥不可能差分飞来去器的分析方法构造了不可能差分路径，分别如图4 和图5所示。

图5 解密方向差分路径

令E0表示5～14 轮，E1表示15～20（21）轮。区分器的密钥关系为K1=K3，K2=K4，K1⊕K2=K3⊕K4=00000000000000020000。E0的2条差分路径均为(00000000,00000020)→(??**?*?*,0?0?2**0)，长度为10 轮。的一条差分路径 为(00000200,00000000)→ (0*0****0,***?***0)，长度为6 轮；另一条差分路径为：(20000000,00000000)→(****?**0,**????**)，长度为7 轮；2条路径的密钥差分均为0。E0的2 条加密路径在第15 轮的输入差分分别为(??**?*?*,0?0?2**),(??**?*?*,0?0?2**)，的2 条解密路径在第15 轮的输入差分分别为(0*0****0,***?***),(****?**0,**????*)，其中下划线标识的4 个半做字节做异或运算一定不为0，满足不可能差分的性质。

在路径的下半段，为使区分器中差分路径尽可能长，本文采用2 条不同长度的差分路径（6 轮和7 轮），这种设计不但不会影响不可能差分的性质，而且还会降低密钥恢复算法的计算复杂度。事实上，由图3 可知，2 对向下加密的路径和2 对向上解密的路径分别加密解密至某相同轮数，对应差分γ、γ′与β、β′只要满足β⊕β′⊕γ⊕γ′≠ 0就满足了不可能差分的要求，而本文设计的不同长度的差分路径是满足该要求的；在此基础上，为完成对23 轮TWINE 算法的分析，只需要分别向下扩展3轮和2 轮，故而密钥恢复算法的计算复杂度也因此有所降低。

4.2 扩展路径

Suzaki 等[7]提出TWINE 算法时，对其S 盒的差分特征给出了如下性质：满足S 盒差分特征（α→β）的输入对的平均对数为，即给定密钥RK 使α→β成立的概率为。利用这个性质，在路径扩展时可以筛除掉多余的明密文对，使算法的计算复杂度大大降低。

本文对不可能差分路径向两端扩展，向上扩展4 轮，如图6 所示，其中，α1∈ΔS(2)，α2∈ΔS(α1),α3∈ΔS(α2),α4∈ΔS(α3),；向下分别扩展2 轮和3 轮，如图7 所示，其中，γ1∈ΔS(2),γ2∈ΔS(γ1),γ3∈ΔS(γ2),,β1∈ΔS(2),β2∈ΔS(β1)。在此基础上最终完成对TWINE 算法的23 轮相关密钥不可能差分飞来去器攻击。符号 ΔS()α表示S 盒输入差分为α时，其输出差分所有可能取值的集合。

4.3 密钥恢复算法

根据图6 和图7 的扩展差分路径，本文对算法进行密钥恢复。具体的过程如下。

步骤1按照图6 中明文差分的输入结构，选取2n个明文结构，每个结构包含402 个明文，它们可以构成2n+79个明文对，记为(P1,P2)，再选择2n+79个这样的明文对(P3,P4)，它们组成22n+158个四元组(P1,P2,P3,P4)。

图6 向上扩展的差分路径

步骤2将四元组中的2 个明文对分别在密钥差分为00000000000000020000 的密钥对下加密23轮，得到对应的密文四元组(C1,C2,C3,C4)。按照图7中密文差分的结构，分别筛除密文差分不满足C1⊕C3=(*000*0*0,020*0000)和C2⊕C4=(*0000020,00*00000)的四元组。经过筛选后，剩余的四元组数为2158+2n×2-104=254+2n。利用4.2 节中S 盒的性质，可以对剩余四元组进行再次筛选。再次筛选后剩余四元组数为≈254+2n×2-31.01=22n+22.99。

图7 向下扩展的差分路径

步骤3猜测，对剩余四元组部分加密一轮，检查输出的四元组中左半部分的第0、1、3、5 个半字节的差分是否为0，若不为 0 则筛除相应的四元组。该步操作后剩余个四元组。该步的计算复杂度为(22n+22.99× 24+22n+17.37×28+22n+11.75× 212+22n+6.13×216)×=22n+20.01。

步骤4猜测，对剩余四元组的(C1,C3)部分解密一轮，检查(C1,C3)对应输出左半部分的第2、3 个半字节的差分是否为0，若不是则筛除相应的四元组。该步操作后剩余 22n-16.35个四元组。该步的计算复杂度为 22n+23.00。

步骤5猜测，对剩余四元组部分加密2 轮，检查输出的四元组中左半部分的第6、7 个半字节的差分是否为0，若不为0 则筛除相应的四元组。该步操作后剩余 22n-16.35个四元组。该步的计算复杂度为 22n+23.00。

步骤 6猜测，对剩余四元组部分加密3 轮，其中，在步骤3 和步骤5 已猜测。检查输出的四元组中左半部分的第1、4 个半字节的差分是否为0，若不为0 则筛除相应的四元组。该步操作后剩余22n-27.59个四元组。该步的计算复杂度为 22n+28.33。

步骤7猜测，对剩余四元组部分加密4 轮，其中已经在步骤 6 中计算得到，在步骤3、步骤5 和步骤6 已猜测，不需要再猜测。检查输出的四元组中左半部分的第2、3 个半字节的差分是否为0，若不为0 则筛除相应的四元组。该步操作后剩余22n-38.83个四元组。该步的计算复杂度为 22n+22.65。

步骤8猜测，对剩余四元组其中的(C1,C3)部分解密一轮，检查(C1,C3)对应输出左半部分的第一个半字节的差分是否为0，若不为0则筛除相应的四元组。对剩余四元组其中的(C2,C4)部分解密一轮，检查(C2,C4)对应输出左半部分的第0 个半字节的差分是否为0，若不为0 则筛除相应的四元组。该步操作后剩余 22n-44.45个四元组。该步的计算复杂度为22n+18.74。

步骤9对(C1,C3)，猜测，共有16 种可能，对剩余四元组进行第 3 轮解密，利用完成筛选，筛选后剩余四元组个数为；对(C2,C4)，猜测，共有16 种可能，对剩余四元组进行第2 轮解密，利用完成筛选，筛选后剩余四元组个数为。该步的计算复杂度为 22n+12.02+22n+17.21。

若在步骤1 中取n=21.05，则步骤9 中剩余四元组个数为 22n-42.07=20.03＞ 1，恰好可以剔除错误密钥，恢复出正确的密钥。

综上，本次23 轮TWINE 的相关密钥不可能飞来去器攻击共可以恢复出68 bit 密钥，需要的明文数为2n+40+1=262.05，计算复杂度为 22n+20.01+22n+14.69+22n+23.00+22n+28.33+22n+22.65+22n+18.74+22n+12.02+22n+17.21=22n+28.39=270.49。与TWINE 算法已有分析结果相比，本文结果在数据复杂度和时间复杂度上都具有一定优势，说明相关密钥不可能飞来去器分析对TWINE 算法具有较好的攻击效果。具体分析结果对比如表8 所示。

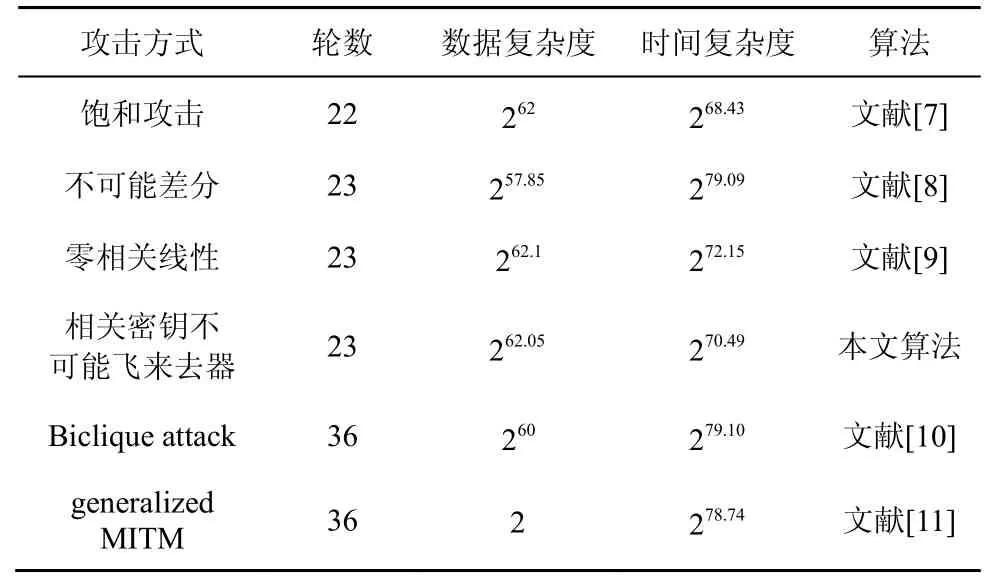
表8 TWINE 的部分分析结果

5 结束语

本文利用TWINE 密钥编排算法的弱点，采用了相关密钥、不可能差分和飞来去器三者结合的手段对其进行了攻击。充分利用了密钥差分对路径的影响，应用飞来去器的方法构造出一条尽可能长的差分分析路径，完成了对23 轮TWINE 的相关密钥不可能差分飞来去器攻击。该攻击需要的数据复杂度为 262.05，时间复杂度为 270.49，与已有分析结果相比具有一定优势。这种将多种分析方法相结合的攻击充分利用了各种分析方法的优势，有利于达到更高轮数的攻击，对于其他分组密码算法的安全性分析也是一种新思路。