基于几何相关的GPS 观测量随机误差模型的研究

周桃云，廉保旺，杨冬冬，张怡，蔡成林

（1.西北工业大学电子信息学院，陕西 西安 710129；2.湖南人文科技学院信息学院，湖南 娄底 417000；3.湘潭大学信息工程学院，湖南 湘潭 411105）

1 引言

GPS 是一种可以实现测距和授时，并能提供全天候、实时、高精度位置、速度及时间信息的导航系统。自1978 年2 月22 日第一颗GPS 卫星发射以来，历经40 年的发展，GPS 的用途早已远远超出了最初的用途。目前，GPS 在精细农业、环境监测、交通运输、资源调查、灾害预报等多个领域得到广泛应用，并对地球科学和大气科学等相关学科的研究起到了极大推动作用[1]。

不论是单点定位技术还是差分定位技术，目前大部分的应用和研究都是基于所有观测到的卫星拥有同样的观测误差，在估计接收机位置时每个卫星观测量都拥有一样的权重，而实际情况下由于大气环境的影响以及卫星仰角的变化，不同卫星观测量的误差是不一样的[2]。在高精度差分定位领域，载波相位整周模糊度的解算是所有定位应用的基础，真实有效的载波相位观测量随机误差模型能够提高整周模糊度的搜索成功率，对高精度定位的应用具有重要意义。

GPS 的定位过程本质上是一个由观测量到参数估计的数据处理过程，通过建立功能模型获得观测量与待估计量之间的数学关系，通过建立随机误差模型获取观测量的随机误差特性，并对估计结果做出评估，最终达到参数估计和精度评定的目的。Gauss 在 1792 年提出的最小二乘（LS,least-squares）方法因其计算方便、思路简洁，成为最为常用且最为重要的数据处理手段之一[3]。为提高LS 的可靠性并得到合理正确的观测量权比，通常采用随机误差模型的后验估计，即方差分量估计（VCE,variance component estimation）为观测量定权。Rao[4]在1971 年提出最小范数二次无偏估计（MINQUE,minimum norm quadratic unbiased estimator），该方法需要已知观测量随机误差模型的一阶矩和二阶矩。Koch[5]在1978 年提出最优不变二次无偏估计（BIQUE,best invariant quadratic unbiased estimator），在正态分布的前提下该方法需要已知观测量随机误差模型的高阶矩。Kubik[6]在1970 年提出极大似然估计（MLE,maximum likelihood estimator）。Koch[7]最早于1987 年使用贝叶斯 (Bayes)方法计算得到VCE 及其置信区间。Teunissen[8]在1988 年提出的最小二乘方差分量估计方法（LS-VCE,least-squares variance component estimation）是近年来受到广泛研究和讨论的方差分量估计方法。LS-VCE 对观测量随机误差模型分布不做要求，而是利用最小二乘原理对方差分量进行估计，统一了功能模型和随机误差模型的估计准则[9-11]，但LS-VCE 并没有为方差分量估计提供一个完美的计算方法，且计算量很大。

对于功能模型，Teunissen[12-13]已经建立了一套权威的定位理论，而随机误差模型尚未有可靠的理论方法。Wang 等[14]利用MINQUE 对3 种基本的观测量随机误差模型进行了估计，但并没有考虑不同类型观测量的方差及其相关性。Teunissen 等[15]对双频信号之间的相关性进行了研究，Hartinger 等[16]建立了载波相位观测量与载噪比之间的模型，Wang 等[17]对时间相关性进行建模之后使用MINQUE 方法对随机误差模型进行估计，并证明了更加真实的随机误差模型可以提高载波相位模糊度解算正确率。整周模糊度解算正确率取决于以下3 个因素[18]：1)观测方程的强度，如功能模型；2)观测量的噪声特性，如随机误差模型；3)整周模糊度解算方法的选择。

Amiri-Simkooei等[19-22]利用LS -VCE 估计了短基线时间序列的噪声状况，并同时考虑不同观测量的方差、协方差、卫星仰角相关性及观测量之间的时间相关性，建立了基于几何无关功能模型的随机误差模型。但在采用LS-VCE 算法对模型进行求解时并没有对LS-VCE 算法进行优化，工作量大。另外，Amiri-Simkooei 也没有考虑接收机时钟不同步引起的卫星位置误差对定位精度的影响。针对此问题，本文主要研究决定整周模糊度解算正确率的第二个因素，建立一种更加真实的随机误差模型并应用于整周模糊度的解算中，以验证模型的有效性。其贡献主要包括：1)在几何相关功能模型中引入误差修正项，以消除或削弱接收机钟差不同步引起的卫星位置误差；2)同时考虑不同观测量类型、不同卫星观测量、卫星仰角相关性及观测量时间相关性，建立一种更加真实的随机误差模型；3)针对LS-VCE 算法计算量大的问题，提出一种以空间换时间的改进LS-VCE 算法并求解随机误差模型；4)采集2 组真实的GPS 数据对所提方法进行性能评估；5)将本文所建立的随机误差模型应用于整周模糊度解算中，并与3 种常用随机误差模型进行比较，验证该模型的可靠性和有效性。

2 改进的几何相关功能模型

几何相关功能模型是利用卫星与接收机之间的几何分布关系，对卫星i到参考接收机r和用户接收机u的距离差值做出近似。一般认为这个距离差值是同一时刻对同一卫星进行观测得到的，事实上由于2 个接收机的钟差及卫星到2 个接收机的传输延时不一致，即使2 个接收机给出了相同的历元时刻，其所对应的信号发送时刻也是不一样的。换句话说，2 个接收机在相同历元时刻得到的观测量分别对应2 个不同的卫星位置i(r)和i(u)，此情况下同时观测卫星i的接收机r和u的几何分布如图1 所示。

图1 考虑不同接收机钟差后的距离单差模型

由于卫星和接收机之间的距离足够远，可以认为r到i(r)的向量和u到i(u)的向量平行。由i(r)和i(u)之间的位置差异引起的距离单差误差，可用i(r)到i(u)的向量在r到i(r)向量的投影来近似表示。接收机r和u观测同一卫星i的单差可表示为

其中，bur为r指向u的基线向量，bi(ur)为i(r)指向i(u)的向量，为r到i(r)的单位向量。

同理，可计算接收机r和u观测同一卫星j的单差及同时观测卫星i和j的双差。

若同时观测m颗卫星，并以第一颗卫星为参考，可得改进的伪距观测量几何相关模型为

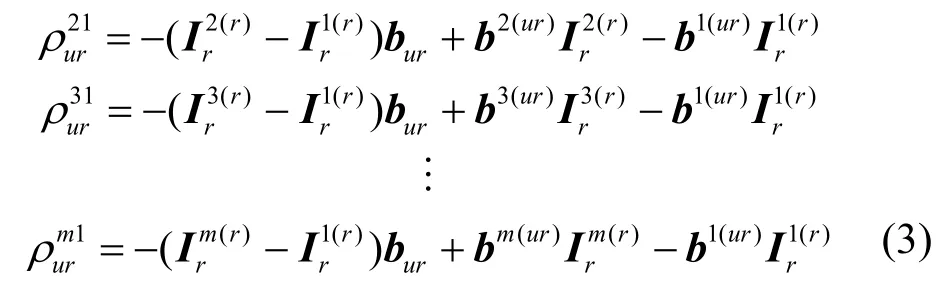
式(3)对应的矩阵表达形式为

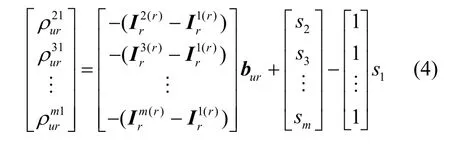
改进的载波相位观测量几何相关模型为

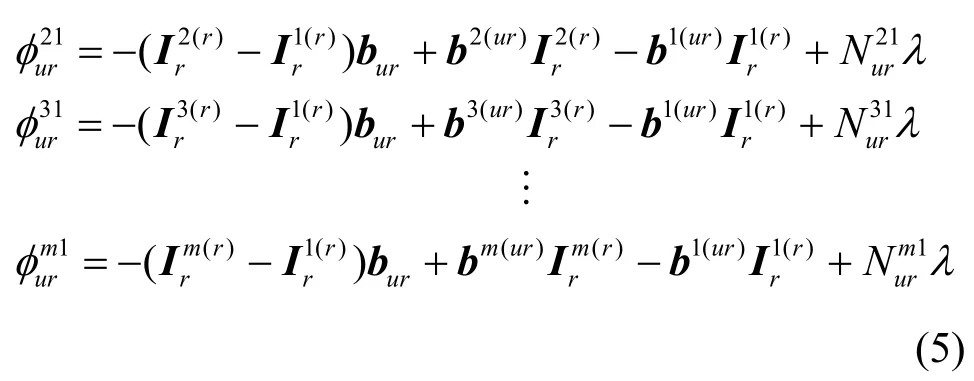
式(5)对应的矩阵表达形式为

由式(4)和式(6)可知，改进的几何相关模型由于添加了误差改正项，能有效消除由差分时刻不同步导致的卫星位置误差。

3 GPS 观测量随机误差模型

一个更加真实的随机误差模型应该包括观测量的方差、不同观测量之间的协方差、卫星仰角相关性及GPS 观测量的时间相关性等多个因素。本节在同时考虑以上4 个因素的基础上建立了一种更加真实的观测量随机误差模型。由于第2 节已建立了几何相关功能模型，对由卫星信号发送时刻不同步引起的误差进行了消除，同时参考文献[19-20]，进行如下假设。

1)忽略同一接收机同时观测到的多个卫星观测量之间的相关性。

2)忽略接收机之间任意2 个卫星观测量之间的相关性。

3)用户接收机和参考接收机同时观测的同一卫星随机误差状况相同。

这些假设不一定是观测量随机误差模型的真实情况，但简化模型中观测量方差比协方差在加权最小二乘中起着更重要的作用，是随机误差模型的主要信息。因此，本文建立的观测量随机误差模型忽略了协方差分量，保留了全部方差分量。此时GPS 观测量随机误差模型可表示为

其中，⊗表示克罗内克积，矩阵C、T、E可分别表示为

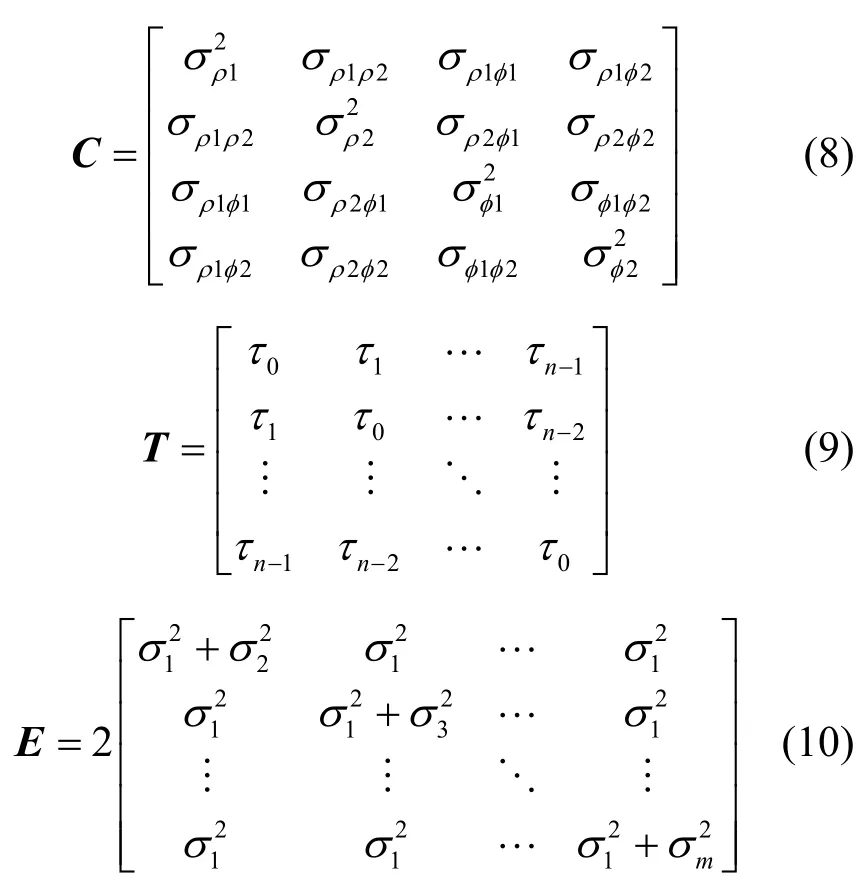
若同时跟踪载波信号L1和L2，则有4 种观测类型，分别为伪距观测量ρ1和ρ2、载波相位观测量φ1和φ2。C为观测类型协方差矩阵，主对角线和非主对角线元素分别表示GPS 观测量的方差和协方差；T为观测量的时间相关性协方差矩阵，主对角线元素表示每个历元的自相关性，理论上取值为1；n为观测历元数；m阶矩阵E是伪距双差观测量，表示与卫星仰角相关的观测量精度，以与仰角θ正弦成反比的函数建模[23]，即

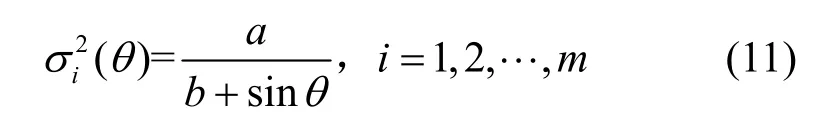
其中，m为观测的卫星数量，并以第一颗卫星作为参考卫星；a、b为模型参数。

4 随机误差模型的求解

4.1 LS-VCE 估计

考虑如式(12)所示的线性观测模型。

其中，E 表示随机变量期望；D表示随机变量协方差；y为m×1 的观测量；A为m×n阶观测方程矩阵；x是n维待估计参数；观测量协方差矩阵Qy可分解成一系列因子矩阵的线性组合；Q0表示协方差矩阵中的已知部分；Qk是构成协方差矩阵的因子矩阵，为已知项，k=1,…,p；σk为待估计参数。

定义观测量残差如式(13)所示。

给定对称正定权重矩阵W，根据加权最小二乘估计准则可得x的估计量为

残差e的估计量为

记P⊥=I-A(ATWA)-1ATW，式(15)可简化为

同样，根据加权最小二乘估计方法可得σk的估计量为

记N=ATWA，z=ATWy，则式(17)简化为

其中，N中第k行第l列元素为

向量z的第k个元素为

算法1基于观测方程矩阵的LS-VCE 计算流程

输入观测方程矩阵A，观测量y，因子矩阵Qk

初始化方差分量迭代初始值σk0,k=1,…,p，迭代控制误差ε，迭代计数i=0

迭代过程在第i次循环中执行步骤1)～步骤5)。

3)计算矩阵N和向量z；

5)i=i+1；当＜ε时，迭代结束。

输出最小二乘方差分量估计，协方差矩阵N-1。

注意到算法1 中步骤3)描述的N为对称矩阵，只需求解下三角或者上三角元素。另外，在计算N和z的过程中频繁使用。为此，本文提出了一种以空间换取时间的改进LS-VCE 方法。

改进的基于观测方程矩阵的LS-VCE 计算流程如算法2 所示。

算法2改进的基于观测方程矩阵的LS-VCE计算流程

输入观测方程矩阵A，观测量y，因子矩阵Qk

初始化方差分量迭代初始值σk0，k=1,…,p；迭代控制误差ε；迭代计数i=0

迭代过程在第i次循环中执行步骤1)～步骤6)。

输出最小二乘方差分量估计，协方差矩阵N-1。

4.2 随机误差模型的迭代分步求解

采用改进的LS-VCE 算法对随机误差模型进行求解需要以下3 个步骤。

step1估计式(7)中的矩阵C。参考文献[21]和文献[22]中，忽略各观测量的时间相关性和卫星仰角相关性，取T为k阶单位矩阵，E可简化为

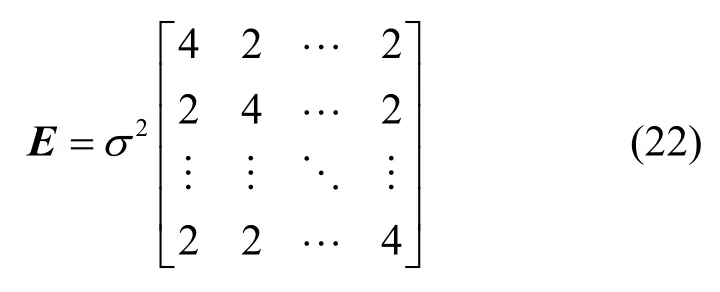
矩阵C中未知的方差和协方差分量采用改进的LS-VCE 算法进行求解。

step2考虑GPS 卫星仰角相关性，将step1 估计得到的矩阵C代入随机误差模型，T仍为k阶单位矩阵，采用改进的LS-VCE 算法求解矩阵E。

step3根据前两步计算得到矩阵C和E，再利用改进的LS-VCE 算法求解矩阵T。基于改进的LS-VCE 算法的迭代分步求解流程如图2 所示。

5 随机误差模型的性能评估

采用2 两组实测GPS数据分别对几何相关功能模型、改进的LS-VCE 算法及随机误差模型进行性能评估。第一组数据是2017 年8 月23 日07:00:00开始采集的，基线长度为2.791 2 m 的2 台接收机和芯星通 UR380 和 NetR9 的GPS 数据；第二组数据是2018 年1 月13 日00:00:00 开始采集的，基线长度为0 的接收机Trimble BD970 的GPS 数据。每组数据持续24 h 同时跟踪L1和L2载波信号，并同时获得载波相位观测量和伪距观测量。

5.1 几何相关功能模型性能评估

直接利用原始观测量得到的接收机伪距和载波相位观测量双差值如图3 所示，图3(a)和图3(c)分别为卫星PRN14和PRN3载波相位双差值和伪距双差值，图3(b)和图3(d)分别为卫星PRN14 和PRN32 载波相位双差值和伪距双差值。

由图3 可知，载波相位观测量精度较高，PRN14和PRN3 的双差值在 ±0.4 m 内波动，PRN14 和PRN32 的双差值在 ±0.3 m 内波动，受差分不同步误差影响比较大。伪距观测量精度较低，PRN14 和PRN3 的双差值在 ±1.2 m 内波动，PRN14 和PRN32的双差值在 ±0.9 m 内波动，虽然也受到差分不同步误差的影响，但在1 ms 的接收机钟差差异范围内，影响程度没有载波相位观测量显著。

图2 基于改进的LS-VCE 算法的迭代求解流程

图3 零基线GPS 数据在3 600 个历元内的观测量双差值

改进的几何相关功能模型首先估算由接收机钟差不一致引起的差分不同步误差，再用该差分不同步误差校正伪距和载波相位观测量的双差值，校正后观测量的双差值如图4 所示。

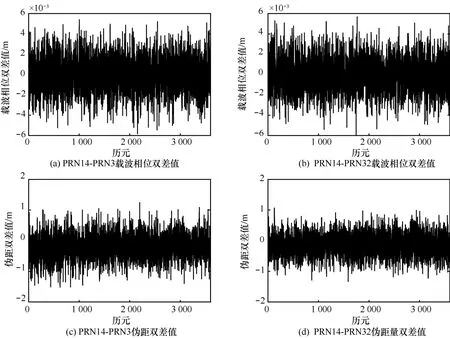
图4 基于改进几何相关模型的零基线GPS 数据在3 600 个历元内的观测量双差值

由图4 可知，改进的几何相关模型能较好地消除由差分不同步引起的误差，得到了零基线载波相位双差值应有的零期望随机噪声结果，PRN14 和PRN3 及PRN14 和PRN32 的载波相位双差值均在±4×10-3m 内波动，较矫正前精度提高了2 个数量级，伪距观测量双差值也同样得到了校正，不过没有高精度的载波相位观测量得到的校正结果显著。

5.2 改进的LS-VCE 算法效率评估

采取以空间换时间的思想，通过减少矩阵乘法和求逆运算对LS-VCE 算法进行改进。为验证算法的性能，在相同的计算平台下对实验中2 组数据的500 个历元分别采用改进前后的LS-VCE 算法进行数据处理，耗时情况如表1 所示。

表1 改进前后LS-VCE 算法的耗时情况

由表1 可知，改进后的LS-VCE 算法其计算效率提高了70%左右，即改进的LS-VCE 算法在不改变精度和无偏性要求的基础上大大提高了计算效率。

5.3 随机误差模型性能评估

根据式(7)所描述的随机误差模型，分别对观测数据进行估计。零基线数据由于没有外部误差干扰，迭代结果与未迭代结果相差不大，因此这里主要对受外界干扰比较明显的短基线数据进行分析，以验证迭代分步求解方法在提高观测量随机误差模型参数估计精度上的有效性。

1)不同观测量的方差估计。通过迭代分步求解得到的4 种类型观测量的方差估计如表2 所示。

由表2 可知，零基线受外部环境误差的影响小，各类型观测量随机误差估计结果比短基线小且稳定。迭代求解后，短基线和零基线各类型观测量的方差估计更加准确稳定，伪距观测量的随机误差标准差都达到亚米级，载波相位观测量的随机误差标准差达到毫米级。

2)不同观测量间的协方差估计。为更清楚地表述各观测类型之间的相关关系，将协方差分量转化为相关系数的形式，通过迭代分步求解法得到的协方差估计如表3 所示。

由表3 可知，L1和L2的相位观测量存在较强的相关性，这是因为2 个载波相位观测量精度与2 个伪距观测量精度相差太大。在零基线情况下，除了2 个载波相位之间的相关性很高之外，其他各观测类型之间都具有零均值的相关性。在短基线数据中，由于外部环境的干扰，观测量精度降低，L1和L2所受的干扰也有差异，载波相位观测量的相关性降低，同时，由于存在对各观测类型一致的干扰，其他各观测类型的相关性有所增长，迭代后短基线数据中L1和L2的相位相关性明显增强。

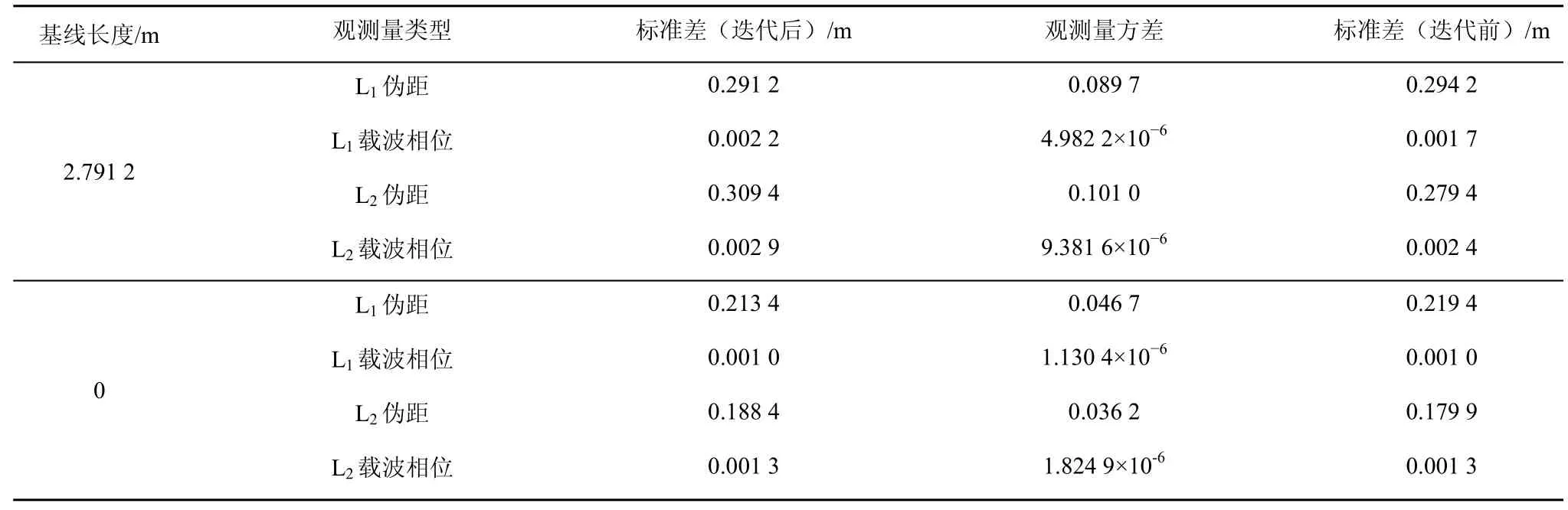
表2 迭代分步法得到的4 种观测量方差估计

表3 迭代分步法得到的不同观测量协方差估计

3)卫星仰角相关性估计。根据PRN8、PRN10、PRN11 和PRN13 这4 颗卫星观测量方差随卫星仰角的变化情况，采用迭代分步法得到的短基线卫星仰角相关误差如图5 所示。其中实线为全局拟合结果，即选取历元时段内所有卫星数据拟合结果，虚线对应卫星在选取历元时段内的拟合结果。

由图5 可知，高仰角情况下卫星观测量方差较小，随着仰角减小，卫星观测量方差显著增大。短基线由于受接收机外部环境误差的干扰，卫星观测量方差有较大幅度的变化。迭代前后拟合出的各组实验数据仰角相关误差模型参数如表4 所示。

由表4 可知，迭代前两组数据的模型参数差异较大，迭代后其差异明显减小。为进一步评估迭代后各类型观测量的方差估计，对短基线数据的载波相位与伪距标准差比值进行分析。短基线数据中L1和L2的相位和伪距观测量标准差比值如图6 所示。

从图6 中可以看出，迭代后各观测类型相对保持稳定，即迭代后的观测量随机误差模型更符合对整个模型的结构化设计。矩阵C从整体上反映各类型观测量的方差和相关性，矩阵E反映各个卫星观测量的方差，迭代求解的过程使2 个矩阵能够更好地分离，每个矩阵的结果都更加准确。

4)观测量时间相关性估计。取5 个连续历元数据进行相关性分析，根据改进的LS-VCE 算法获得C、E和T之后，采用迭代分步法得到的观测量时间相关性如表5 所示。

图5 采用迭代分步法得到的PRN8、PRN10、PRN11 和PRN13 这4 颗卫星短基线数据仰角相关误差

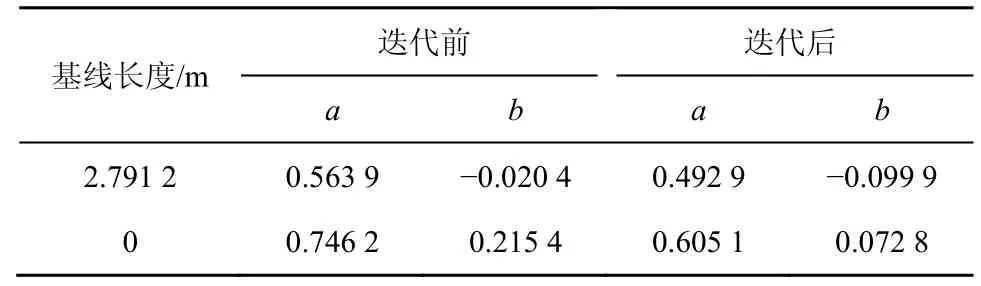
表4 迭代前后仰角相关误差模型参数

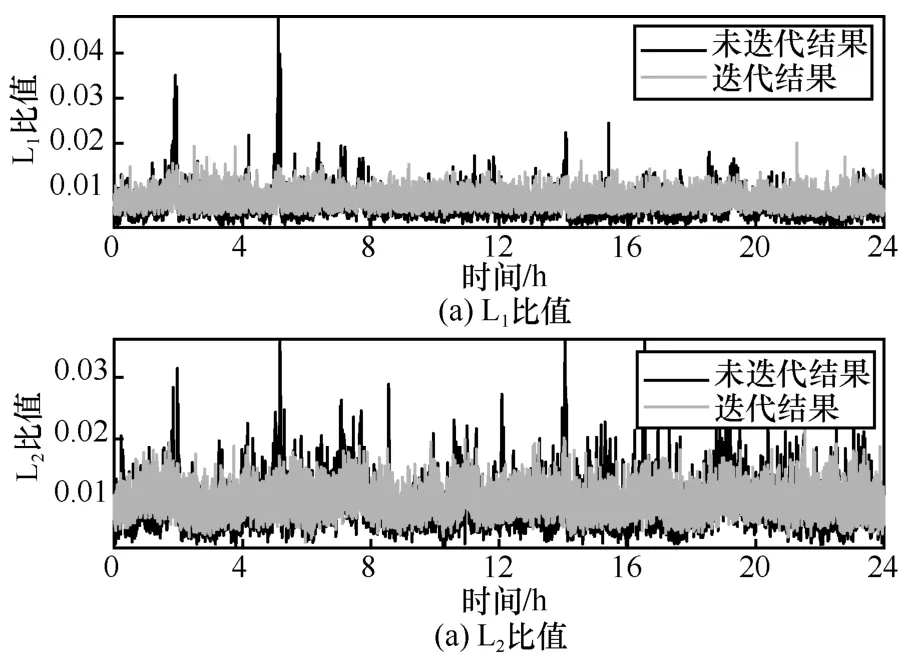
图6 短基线数据载波相位与伪距标准差的比值

由表5 可知，2 组数据的时间相关性都随着时间间隔的增加而减小。迭代前零基线各历元数据之间几乎无关，从第二个历元开始相关性就接近于0。而短基线各历元数据由于多径效应等外界因素的影响，时间相关性在5 个历元之后还保持在0.4 以上，迭代后各观测量的时间相关性比迭代前高。

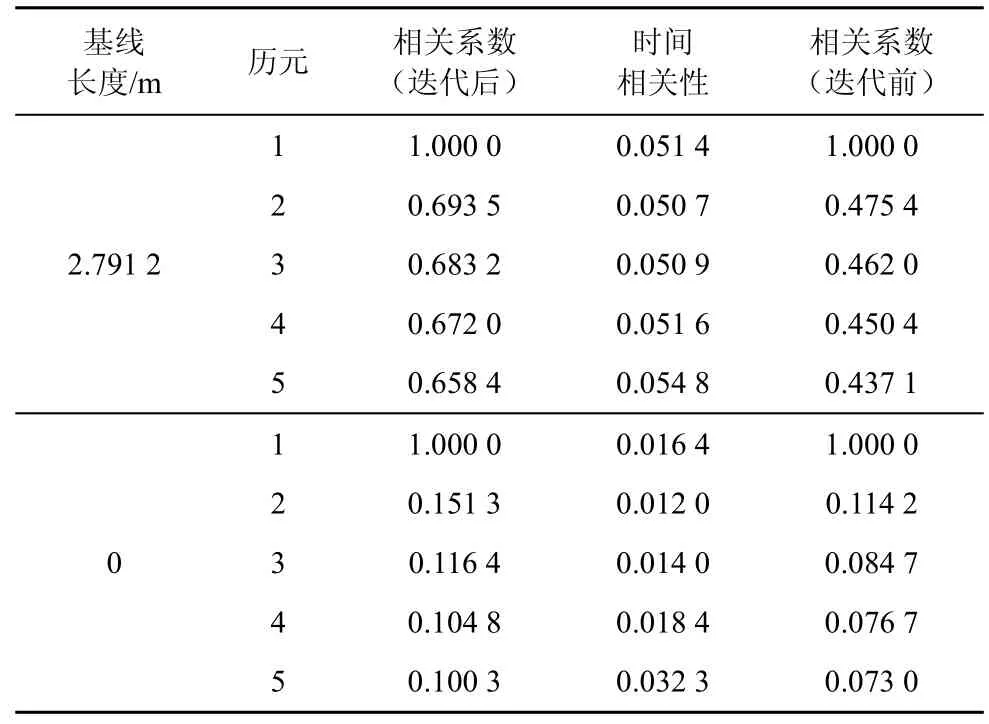
表5 迭代前后GPS 观测量的时间相关性

6 随机误差模型在整周模糊度解算中的应用

载波相位整周模糊度解算是高精度定位应用中的一个重要问题，在整周模糊度解算过程中，一般采用LAMBDA 算法搜索最小二乘整数解时需要得到浮点解协方差矩阵，而浮点解协方差矩阵是通过误差传播式由观测量协方差矩阵获得，因此观测量的协方差矩阵，即观测量随机误差模型对整周模糊度的解算有很大影响。本节将研究分析不同观测量随机误差模型对载波相位整周模糊度解算的影响。

根据观测量随机误差模型的准确度，在整周模糊度解算实验中将观测量随机误差模型分为4 种。

模型1不考虑随机误差，假设各观测量具有相同的测量精度，观测量协方差矩阵为单位阵，不考虑各观测量之间的差异以及相关性。

模型2只考虑伪距观测量和载波相位观测量之间的差异，不考虑各观测量之间的相关性及观测量自身的差异和相关性。

模型3考虑不同观测量之间的差异，观测量随机误差模型采用式(11)所示的拟合函数。

模型4本文所建立的观测量随机误差模型，每5 个历元为一个分组，假设2 个相邻分组具有相同的随机误差模型，将前一分组的估计值作为后一分组中随机误差模型的初始值。

利用4 种随机误差模型对短基线和零基线24 h的卫星观测数据进行载波相位整周模糊度解算实验，所有实验均采用单频单历元模糊度解算方法，得到整周模糊度解算正确率情况如表6 所示。

由表6 可知，在完全不考虑观测量随机误差模型的情况下，整周模糊度解算的正确率很低，最高只有11.237%。将伪距和载波相位观测量的经验值代入随机误差模型后，整周模糊度解算的正确率得到极大提升，最高达到99.785%，最低也有84.033%。再将观测量卫星仰角相关模型引入随机误差模型，对观测量的估计更加准确，整周模糊度解算正确率继续提高，最高达到99.789%，最低也有87.428%。本文所建模型的解算正确率比前3 种都高，最高可达到99.847%，最低也有92.549%。另外，在解算L1时，模型 4 的成功率为 92.549%，略高于Amiri-Simkooei[18]的成功率92.500%，在解算L2时，模型4 的成功率为95.714%，与Amiri-Simkooei[18]的成功率95.200%相比，高出0.514%。

表6 2 组数据整周模糊度正确率情况

实际应用常采用比例检测法确认整周模糊度，当比值大于某一阈值时最优整数解为正确解，否则为错误解。短基线和零基线2 组数据在4 种模型下的整周模糊度解算误报率和错检率情况分别如图7和图8 所示。

图7 4 种模型下L1、L2短基线数据整周模糊度解算误报率和错检率

图8 4 种模型下L1、L2零基线数据整周模糊度解算误报率和错检率

由图7 可知，模型4 的误报率最低且差异很小，模型1 的误报率明显高于其他3 种模型，即随机误差模型越准确，整周模糊度解算误报率越小。4 种模型在错检率方面的区别不大，由于模型4 的整周模糊度错误数量比较少，L2频率中的错检率略高。由图8 可知，对于零基线数据，模型1 的误报率明显高于其他3 种模型，模型4 仍保持较低的误报率，在错检率方面4 种模型没有明显的差异。

7 结束语

实际研究和应用中，随机误差模型考虑的因素越细致，越能反映观测量的真实误差状况。为此，本文研究了一种基于几何相关功能模型的观测量随机误差模型。首先，为消除或削弱接收机钟差不同步引起的卫星位置误差，在几何相关功能模型中引入误差修正项对几何相关功能模型进行改进，实验结果表明，改进后的双差观测量精度提高了2 个数量级；其次，为降低LS-VCE 算法的计算量，提出一种以空间换时间的改进的LS-VCE 算法，实验结果表明，与传统的LS-VCE 算法相比，改进后的LS-VCE 算法在求解短基线和零基线随机误差模型时，其耗时分别节省了69.8%和71.2%；最后，利用2 组真实的GPS数据对所建的随机误差模型进行了性能评估，并采用该模型解算载波相位整周模糊度，实验结果表明，在解算L1和L2时，该模型的成功率均高于Amiri-Simkooei 所提方法。