遥控履带车车架有限元模态分析
施炎

【摘 要】履带车在行驶的过程中常承受多源复杂激励作用而产生振动,影响履带车监控性能及工作寿命。以全国大学生市级创新训练项目“电磁辐射实时监控无人车”为例,借助三维建模软件Solidworks建立其三维模型,而后将车架模型导入ANSYS有限元分析软件中进行离散化处理,并基于Block Lanczos算法求解车架振动模态。分析结果表明,小车固有的模态不会与小车特征频率合拍,不会产生共振问题。
【Abstract】 Tracked vehicles often suffer from multi-source complex excitation during driving, which results in vibration, and affects the monitoring performance and working life of tracked vehicles. Taking the municipal innovation training project "Real-time monitoring of electromagnetic radiation unmanned vehicle" as an example, the three-dimensional model of the unmanned vehicle is established by using the three-dimensional modeling software Solidworks, then the frame model is imported into ANSYS finite element analysis software for discretization, and the vibration mode of the frame is solved based on the Block Lanczos algorithm. The analysis results show that the inherent modes of the vehicle do not match the characteristic frequencies of the vehicle, and there is no resonance problem.
【關键词】履带车;车架;三维建模;振动模态;有限元法
【Keywords】tracked vehicle; frame; three-dimensional mode of vibration; vibration mode; finite element method
【中图分类号】U463.6 【文献标志码】A 【文章编号】1673-1069(2019)07-0175-03
1 引言
履带车在行驶的过程中会受到各种激励作用,如路面不平造成的位移激励,电机转子存在偏心造成的内部激励等。车架作为整车的骨架,连接着各个机构总成,支撑整车的重量,承受外部荷载的作用,因此车架必须具有足够的刚度和强度来承受车自身的载荷和来自外部的冲击。
模态分析是研究车辆结构动力学性能的一个重要方法。理论上,结构具有多少个自由度,就对应有多少个固有频率,结构在每一阶固有频率下振动都对应一个固有模态振型。模态分析方法包括计算模态分析和试验模态分析方法两种,本文基于ANSYS有限元分析软件,即采用计算模态方法对履带车的车架进行模态分析,对其振动特性做出评价。
2 模态分析理论
设n多自由度系统自由振动微分方程:
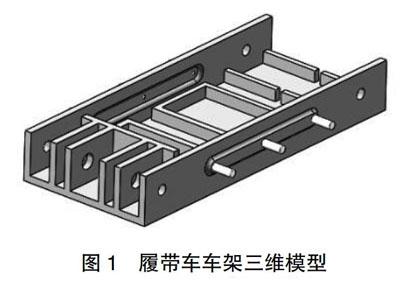
3 履带车车架三维建模
根据实际功能要求,在SolidWorks三维建模软件中对履带车车架进行建模,模型如图1所示,并导出x_t格式的模型,将模型导入ANSYS软件进行前处理。
4 履带车有限元建模
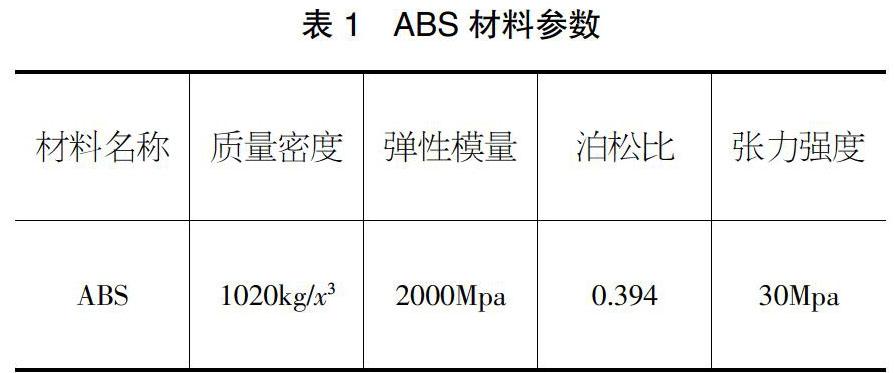
在ANSYS Workbench操作界面中,添加Modal模态分析模块,将模型导入后,先耦合各零部件,在Mesh模块中对车架模型进行网格划分,采用Sizing和Face Meshing两种划分方法对网格进行适当加密,网格节点数为315071,单元数为197525。定义车架材料,车架材料为ABS材料,材料属性如表1所示。
5 履带车车架模态分析
5.1 履带车车架自由模态分析结果
基于ANSYS Workbench有限元分析软件的求解器对履带车车架进行模态分析,因车架的前六阶固有频率值为0或接近于0,因此可以判断出前六阶模态为刚体模态,代表了履带车车架的刚体位移,而刚体模态对振动分析并没有实际意义,所以去除前六阶刚体模态,主要针对后四阶自由模态振型进行分析,后四阶模态振型分析结果如表2所示。因篇幅限制,自由模态分析结果只列出其中非刚体模态中第1阶和第4阶的模态振型如图2、图3所示,各阶振型固有频率与振型描述如表2所示。
5.2 履带车车架自由模态分析结果评价
由对履带车车架的前四阶自由模态分析结果可知,履带车的1阶振型为扭转振型,其最大幅值出现在车架侧壁后段的上顶角处;2阶振型为弯曲振型,其最大幅值出现在车架底盘后段的中心部位;3阶振型为侧向弯曲振型,其最大幅值出现在车架侧壁中后段的上表面;4阶振型为侧向弯曲振型,其最大幅值出现在车架侧壁前段的上顶角处。
5.3 履带车车架预应力模态分析结果
首先根据履带车在实际工作过程中的载重情况,将驱动器、电池、摄像头等仪器的重量添加至车架上,并施加重力场,再将小车的支撑轴固定,研究车架在該预应力情况下的模态振型,其第1阶和第6阶预应力模态振型如图4、图5所示,各阶振型固有频率与振型描述如表3所示。
5.4 履带车车架预应力模态分析结果评价
由ANSYS Workbench分析出的履带车车架的预应力分析结果可知,1阶振型为车架后段弯曲振型,最大幅值出现在车架底盘后端边缘中心处;2阶振型为车架后段扭转振型,最大幅值出现在车架侧壁后段的上顶角处;3阶振型为车架中段弯曲振型,最大幅值出现在车架底盘中部对称平面处;4阶振型为车架后段弯曲振型,最大幅值出现在车架侧壁后段的上顶角处;5阶振型为车架后段扭转振型,最大幅值出现在车架最后端的壁面上;6阶振型为车架后段扭转振型,最大幅值出现在车架侧壁后段的下顶角处。
假设电机转子转动时存在偏心力,履带车快速行驶速度为1.5m/s,主动轮的直径为45mm,电机轴与主动轮直接通过联轴器连接,则激振力的频率等于电机转动频率f=10.610Hz,小于49.599Hz,因此,在满足相应功能要求下,电机转动不易与车架产生共振。
6 结论
运用ANSYS Workbench有限元分析软件对履带车车架进行模态分析,得到了车架自由模态前4阶模态振型和预应力模态前6阶模态振型以及各阶模态对应的固有频率,并分析出履带车车架在各模态振型中运动幅值最大的部位。结合履带车的实际工作需要,当履带车以1.5m/s的速度行驶时,电机的运转频率f=10.610Hz低于预应力模态中一阶频率49.599Hz。因此,车架固有模态不会与小车工作特征频率合拍,不会产生共振。
【参考文献】
【1】任可美,戴作强,郑莉莉,等.纯电动城市客车底盘车架的模态分析与优化[J].制造业自动化,2018,40(01):45-50+64.
【2】潘宇.某车型副车架结构强度与模态分析及结构改进[J].机械强度,2017,39(06):1490-1494.
【3】任锦涛,李建军,杜明轩.基于ANSYS的车架有限元模态分析[J].汽车实用技术,2019(10):141-142+162.

