夏季无空调系统室内平均温度仿真计算
郭树生 廖火生 李建维
【摘 要】论文依据能量守恒定律,建立了适用于计算多房间建筑夏季空调系统失效后室内平均温度的仿真模型,可以快速求得各个房间的平均温度,得到热量传递的过程。论文所建立的仿真模型在进行适应性改进之后,可适用于不同形状和结构的建筑计算室内的平均温度。
【Abstract】Based on the law of conservation of energy, this paper establishes a simulation model suitable for calculating the indoor average temperature of multi-room buildings after the failure of air-conditioning system in summer, which can quickly obtain the average temperature of each room and obtain the heat transfer process. After the adaptability improvement, the simulation model established in this paper can be applied to calculate the average indoor temperature of buildings with different shapes and structures.
【关键词】多房间建筑;室内;平均温度;仿真
【Keywords】multi-room building; indoor; average temperature; simulation
【中图分类号】TM623.8;TP391.9 【文献标志码】A 【文章编号】1673-1069(2019)07-0128-03
1 引言
夏季空调房内设备正常稳定运行所需的温度将由空调系统进行维持。在核动力平台中,基于纵深防御的设计理念,通常会放置专设安全设施。在严重事故工况下,空调系统由于失去应急电源而无法正常工作,而一些专设安全设施还需要继续投运,以保证核安全。为了确保这些设备在失去空调系统后还能稳定运行,需要在设备设计制造的时候提出更加严苛的温度条件[1]。提出的温度范围过大,会使得设备的设计制造难度加大,同时,经济性大大降低;若温度范围过小,可能造成设备无法在实际的事故工况下运行,威胁核安全。
失去空调系统后,内部设备散发的热量需要依靠空气的自然对流以及热辐射传递出去。对于单个房间而言,可以很容易地建立CFD计算模型进行数值分析,获得房间内部详细的温度场,并进行评估。而建筑存在多个房间时,由于各个房间的温度边界相互耦合,无法对各个房间进行单独分析[2]。若采用数值方法,需要全建筑范围建模,难以实现。对于空调系统的设计而言,室内平均温度是一个重要的技术指标,采用能量守恒关系求解房间的平均温度显得更为容易,唐娟等[3]、申昭辉等[4]进行了这方面的研究。但是研究提出的方法、模型都是针对单个房间,而对整栋建筑内各个房间温度的预测还缺乏相应的研究。本文从能量守恒角度出发,建立多房间的平均温度预测模型,获得各个房间的平均温度以及能量传递过程,为全建筑范围的室内温度评估提供指导与参考。
2 建模方法
2.1 室内平均温度数学模型
根据房间的能量守恒定律,单位时间内房间的能量变化率等于通过围护结构流入和流出房间的能量差加上房间内的热源释放的能量,即满足以下能量守恒方程:
式(1)中,cp——空气定压比热(J/kg·℃);
ρ——空气密度(kg/m3);
V——房间体积(m3);
tn——房间平均温度(℃);
τ ——时间(s);
hi——房间第i个面与外界(包括相邻房间)的综合换热系数(W/m2·℃);
Ai——房间第i个面的面积(m2);
ti——房间第i个面外界(包括相邻房间)的平均温度(℃);
Q——房间内部总散热量(W)。
2.2 仿真模型的建立
根据能量守恒方程式(1)所示,建立规则六面体房间的平均温度仿真模型,房间含有6个面,每个面包含综合换热系数、换热面积和外部温度三个输入变量,外部边界为相邻房间时,以相邻房间的平均温度作为外部温度。房间内部包含空气密度、空气比热、房间体积以及房间总散热量四个输入变量,因此单个房间模型总共包含22个输入变量和一个输出结果即房间内部平均温度(如图1)。
3 计算结果及分析
3.1 单个房间平均温度计算
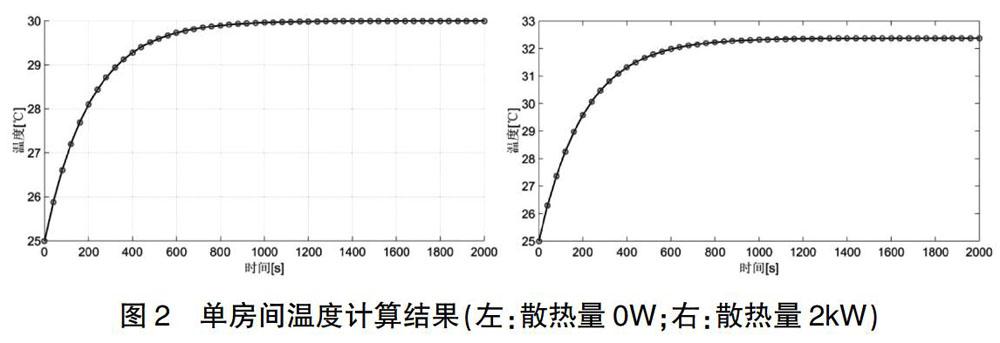
建立一个长、宽、高分别为6m、6m、4m的方形房间,假设六个面的综合传热系数均为5W/m2·℃,外部环境温度为30℃,房间初始温度为25℃,房间内部散热量分别按0W(无热源)和2kW考虑,空气密度1.2kg/m3,定壓比热1005J/kg·℃,计算结果如图2所示。可以看出温度达到稳态后,无散热量的房间平均温度等于外部环境温度;而散热量为2kW时,平均温度最终趋于32.38℃,高于外部环境温度,以上结果满足能量守恒规律。
3.2 多房间平均温度计算
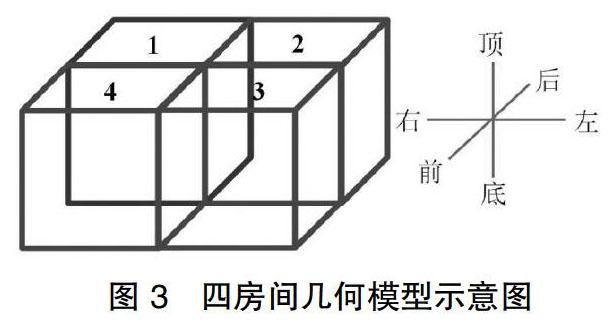
建立如图3所示的四房间模型,各个房间的长、宽、高分别为6m、6m、4m。假设每个房间六个面的综合传热系数均为5W/m2·℃,外部环境温度为30℃,各房间初始温度为25℃。其中1号房间的内部散热量为2kW,2号房间的内部散热量为4kW,其余房间无散热量。
建立多房间平均温度仿真模型如图4所示。
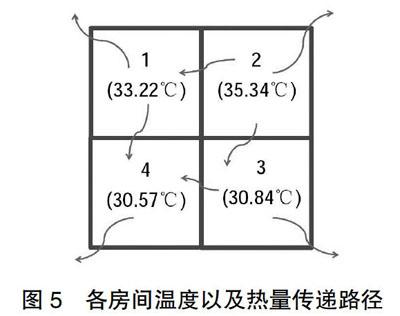
对上述四房间温度模型进行求解,温度达到稳态时,四个房间的温度依次为33.22℃、35.34℃、30.84℃和30.57℃,据此可以分别得出各个房间的热量传递值,结果如下。
1号房间:从2号房间传递而来254.4W,传递至4号房间318W,传递至外部环境1932W。
2号房间:传递至1号房间254.4W,传递至3号房间540W,传递至外部环境3204W。
3号房间:从2号房间传递而来540W,传递至4号房间32.4W,传递至外部环境504W。
4号房间:从1号房间传递而来318W,从3号房间传递而来32.4W,传递至外部环境342W。
各个房间的热量传递过程如图5所示,其中曲线箭头表示热量传递方向。以上结果符合温度分布规律,证明了建立的多房间仿真模型的正确性。
4 结语
基于能量守恒定律建立的单房间与多房间的平均温度仿真模型,可以快速地计算无空调系统室内的平均温度,获得各房间的热量传递过程。该方法适用于多房间相互耦合的建筑夏季无空调系统室内环境温度的评估,为专设安全设施的设计制造提供环境条件,并且满足动态外部环境边界条件,可拓展到全天候的温度计算。同时,对本文建立的仿真模型进行适应性修改,可以适用于不同形状和结构的建筑计算平均温度。
【参考文献】
【1】杨伟,薛思浩,吕亚飞.等.不同屋顶结构下室内自然对流传热数值分析[J].四川大学学报(自然科学版),2012,49(6):1301-1306.
【2】常建国,薛思浩,杨琳琳.不同热源位置下室内自然对流换热数值模拟[J].土木建筑与环境工程,2012,34:17-20.
【3】唐娟,魏兵,石舒健.基于Matlab/Simulink的某空调系统能耗仿真分析[J].建筑热能通风空调,2010,29(2):53-57.
【4】申昭辉,王汉青.Matlab/Simulink在空調系统中的应用[J].南华大学学报(理工版),2003,17(1):16-20.

