某型装甲车辆底盘关键部件综合检测系统抗干扰性能预测*

孙兴飞 周凤潮 纪伟虎 段疆宏 葛希波

（解放军66157部队 保定 072653）

1 引言

某型装甲车辆底盘关键部件综合检测系统的结构框图如图1所示，主要由硬件和软件两大部分组成。硬件部分包括各类传感器、模块化信号调理器、数据采集控制器和计算机；软件部分包括多通道数据采集软件、通用信号分析与处理软件、关键部件技术状况评估与故障诊断软件［1]。

准确可信地评估某型装甲车辆底盘关键部件综合检测系统抗干扰性能有助于了解、掌握该系统在干扰条件下的工作状态，明确其能力和不足，同时可为该系统的后续改进研制和实际操作提供可靠的参考依据。

图1 某型装甲车辆底盘关键部件综合检测系统结构框图

2 某型装甲车辆底盘关键部件综合检测系统抗干扰性能评价指标体系

2.1 确定评价指标

评价某型装甲车辆底盘关键部件综合检测系统抗干扰性能主要基于三个方面：传感器、信号调理器和数据采集控制器。同时传感器、信号调理器和数据采集控制器的抗干扰性能分别受各自子因素影响［1～5]（见图2）。

图2 某型装甲车辆底盘关键部件综合检测系统抗干扰性能评价指标体系

2.2 确定评价等级

将指标分为优、良、中、合格、不合格五个等级，分别赋予相应的分值9，7，5，3，1。根据灰色评估理论［6～7]，本文中5个指标评分等级对应5个评价灰类，其相应的灰数和白化权函数如下：

确定评价灰类就是要确定评价灰类的等级数、灰类的灰数以及灰数的白化权函数。

3 基于层次分析法预测系统抗干扰性能［8～9]

3.1 构建判断矩阵

结合专家经验，对于 U1，U2，U3，其判断矩阵为

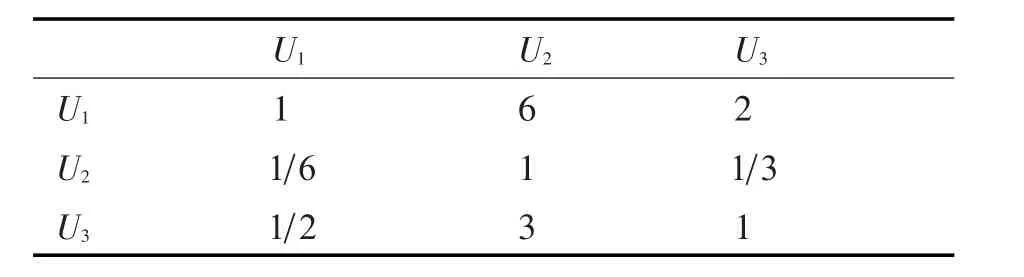
表1 判断矩阵

3.2 计算判断矩阵的各行元素的积的n次方根

对于本例，n=3，则：

ωˉ1=2.2894，ωˉ2=0.3816，ωˉ3=1.1447，并将其归一化得到：ω1=0.6000，ω2=0.1000，ω3=0.3000。

3.3 判断矩阵的一致性检验

CI=(λmax-n)/(n-1)=0.00005，其中λmax为判断矩阵的最大特征值。判断矩阵的随机一致性指标CR=CI/RI＜0.1（RI为常数），判断矩阵具有满意一致性。故 U1，U2，U3的指标权重分别为 0.6000，0.1000，0.3000。

同理可算出指标 U11，U12，U13，U21，U22，U31，U32各自权重分别为［0.1 0.2 0.7]；［0.3 0.7]；［0.7 0.3]。

3.4 预测抗干扰性能

EAHP=0.6*［0.1 0.2 0.7]*［1 10 2]’+0.1*［0.3 0.7]*［2 5]’+0.3*［0.7 0.3]*［5 10]’=4.46（式中的整数矩阵部分可根据判断矩阵，再结合白化权函数得到）。

4 模糊综合评判法预测抗干扰性能［10]

由层次分析法可知，评判因素集U=［U1，U2，U3]=［0.1 0.2 0.7]；其中子因素集 U1=［U11，U12，U13]=［0.6000，0.1000，0.3000]；子因素集 U2=［U21，U22]=［0.3 0.7]；子因素集U3=［U31，U32]=［0.7 0.3]。

4.1 确定模糊关系矩阵

模糊关系矩阵根据判断矩阵和白化权函数得到。

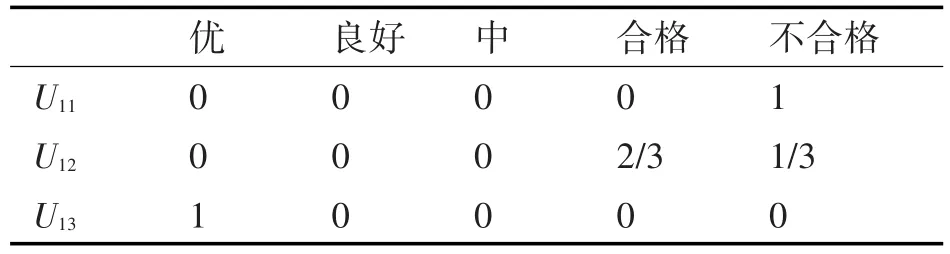
表2 模糊关系矩阵R1

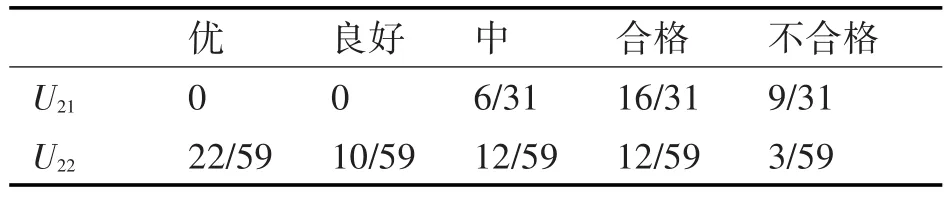
表3 模糊关系矩阵R2

表4 模糊关系矩阵R3

4.2 预测系统抗干扰性能

初 级 评 判 结 果B1=U1*R1=［0.3000 0 0 0.0667 0.6333]，

最终评判结果为B=U*［B1；B2；B3]=［0.1359 0.0711 0.2464 0.3254 0.2213]；

故预测值为Q=B*［9 7 5 3 1]=4.1503。

5 最大熵原理预测系统抗干扰性能［11]

5.1 最大熵原理

1948年，香农（Shannon）用熵来定量地描述一个随机事件的不确定性或信息量：

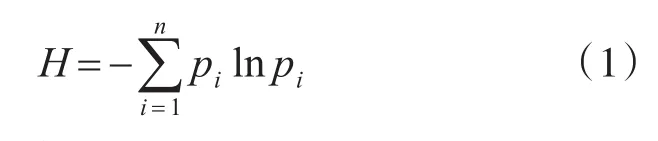
式中H称为信息熵，熵H是pi的泛函，因此存在一个使H取极大值的分布。相应的概率分布满足：

且若干已知函数fk(xi)的平均值Ek是给定的，即

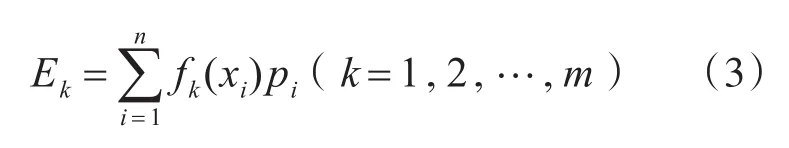
利用拉格朗日乘子式：

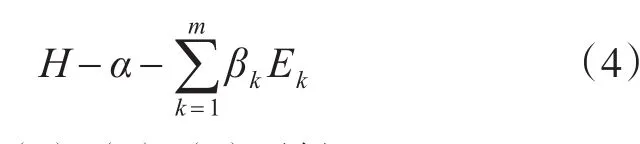
同时联立式（1）、（2）、（3）可得

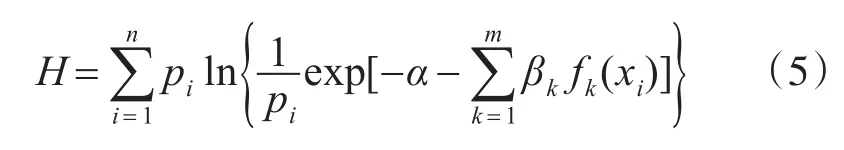
又由于 lnx≤x-1，则

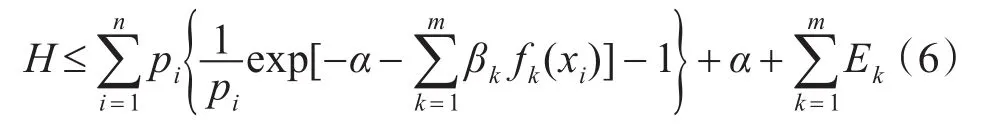
根据最大熵原理，当且仅当

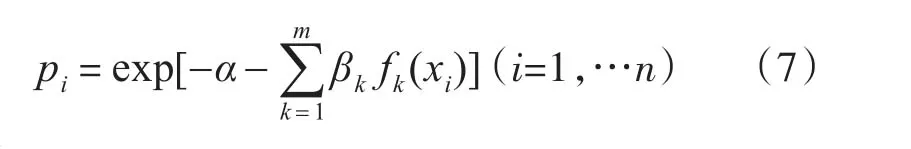
时，H取得最大值。

5.2 预测系统抗干扰性能

由于影响某型装甲车辆底盘关键部件综合检测系统抗干扰性能的因素有很多，不确定性很大，如果采用单一方法预测，预测误差较大；如果采用最大熵原理的方法对传统方法的预测结果进行综合运用，即以前述的各种预测结果作为约束条件，求出最大熵的分布，预测误差将会大大降低。根据最大熵原理，建立模型如下［12]：

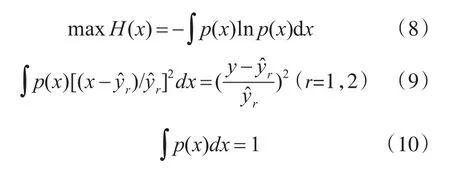
联立可求得参数α和βk，进而求得

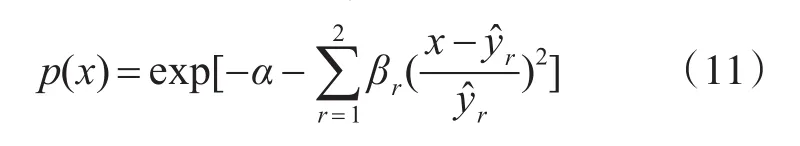
最后通过求期望值即可预测出系统的抗干扰性能。则联立（9）、（10）、（11）可得：

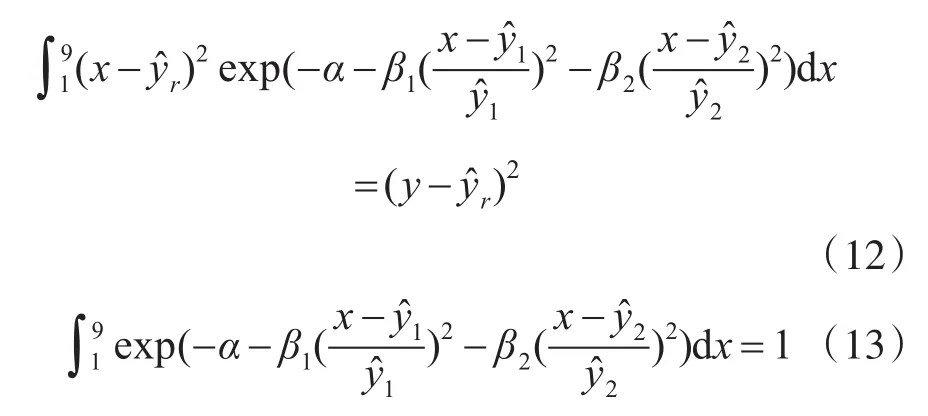
其中y为抗干扰性能实际值，这里取7。

联立（12）、（13）可得到：α≐ 2，β1≐ 42.04，β2≐ -31.11，则

6 结果分析

7 结语

当影响某型装甲车辆底盘关键部件综合检测系统抗干扰性能的随机且不确定的因素很多时，可以采用最大熵原理的方法对各种传统模型的预测结果进行综合，求出最大熵的分布，准确度将大大提高。