城市不透水地表降雨径流系数变化规律分析
王萌萌,刘文龙,申红彬
(1.东营市水务局,山东 东营 257091;2.华北水利水电大学水利学院,河南 郑州 450045)
近年来,随着GIS技术的发展,地表糙度测量进入到了一个全新的发展阶段。有测量研究指出,地表填洼量与坑洼深度和坑洼面积密切相关,变化呈二次抛物线规律,并且填洼量随着地表坡度的增加而减小。Linsley等认为土壤填洼量增量随着降雨的进行按照指数形式衰减。在Linsley公式中,降雨量本质上反映了地表积水深度对地表填洼损失的影响。而在实际过程中,由于坡面径流作用,地表积水量并不等于降雨量。目前,人们在不透水地表填洼损失计算中对坡面径流运动的影响考虑较少。本文在上述研究工作的基础上,考虑不透水地表降雨径流对填洼损失的影响,基于水量平衡原理深入研究不透水地表降雨径流系数的变化规律。
1 坡面径流运动下的地表积水量计算
根据等流时线理论,假设降雨历时t等于坡面汇流时间τ,矩形坡面出流过程线可简化为以Qm为高,以2τ为底宽的等腰三角形,如图1所示。0~2τ时段内,坡面出流过程线方程式为:
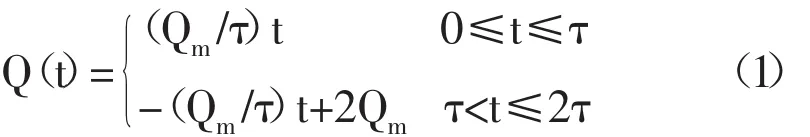
式中:Q为坡面出口流量;t为时间;Qm为洪峰流量;τ为坡面汇流时间。
按照等腰三角形面积求法,坡面出流总量W=Qmτ,应与坡面上的降雨总量Iτ相等,可得:
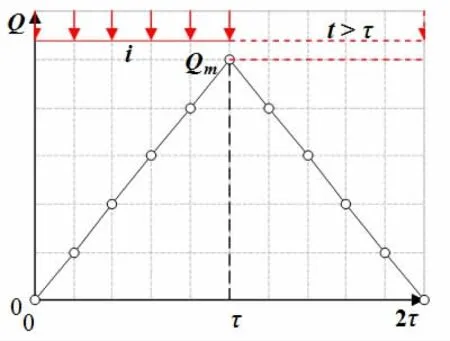
图1 矩形坡面推理公式法出流示意图

式中:Qm同前;I为降雨强度;F为坡面面积。
根据水量守恒原理,0~τ时段内,坡面径流作用下地表积水深可采用式(3)计算:
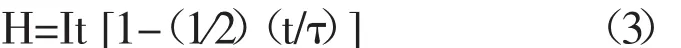
式中:H为坡面蓄水深;其余符号同前。
式(3)中,坡面蓄水深的最大值为Iτ/2。如果降雨历时t大于坡面汇流时间τ,则τ~t时段内的坡面积水深保持为Iτ/2,相应变化情况如图2示。
坡面汇流时间τ的计算式为:

式中:L为坡面长度;V为坡面水流平均流速。
2 不透水地表降雨径流系数变化规律

图2 矩形坡面积水深变化过程
对于不透水地表,雨水下渗损失近似为零,暂不考虑植被地表的截留,场次降雨在扣除汇水区蒸发、填洼损失后,地面开始积水,形成地表径流。考虑到蒸发损失量相对较小,可以忽略不计,因此,其水量平衡基本关系式可简化为:

式中:R为径流量;P为降雨量;Δ为填洼损失量,Δ一般按照Linsley公式计算:

式中:Δmax为最大填洼损失量;k为变化速率,k=1/Δmax。
对于均匀雨强,对式(6)求导,则可得到不透水地表降雨填洼速率的表达式:

式中:ε为填洼速率;其余符号同前。
由式(7)可知,不透水地表填洼速率在初始时刻与雨强相等,而后逐渐减小,则在初始时刻后就会产流。而实际上,不透水地表上的降雨只有在满足一定初损后才会有径流出现。大量研究表明,不透水地表降雨初损值一般为最大填洼损失量的1/3左右。以产流时刻为初始时间,则地表填洼量的最大值为2Δmax/3,而变化速率依然为k=1/Δmax。另外,在式(7)中,降雨量 P 本质上反映了地表积水深度对填洼损失的影响。而在实际降雨径流过程中,由于坡面径流作用,地表积水量并不等于降雨量。因此,在式(6)的基础上,可将地表填洼量公式改写为:
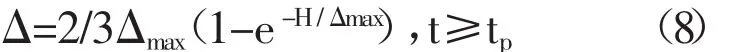
式中:tp为产流时间,tp=Δmax/3/I,其余符号同前。
图 3、4 分别为式(6)、(8)对应的降雨量或地表积水量、填洼量的变化示意图。从中可以看出,考虑坡面径流作用后,不透水地表降雨填洼损失量有所减小。
根据降雨径流系数的定义,不透水地表的场次降雨径流系数可以表示为
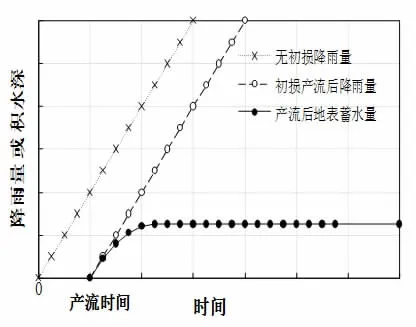
图3 公式(6)、(8)降雨量、地表积水量变化示意图

图4 公式(6)、(8)地表填洼量变化示意图

式中:Ψ为场次降雨径流系数;Δt为降雨历时;其余符号同前。
3 应用实例分析
3.1 数据来源
文献对多种不同类型的不透水地表进行了室内模拟降雨径流试验,并给出了较为详尽的径流系数统计数据。各下垫面均为1m×10m,坡度为0.5%。其中,SBS是目前屋顶广泛采用的一种防水材料。表1为SBS下垫面不同雨强条件下的产流时间,分别计算初损并取其算术平均值,约为 0.47mm。图 5为 0.23mm/min、0.46mm/min、1.0mm/min三组雨强试验条件下的SBS下垫面涨水曲线。表2为模拟统计计算得到的涨水曲线特征参数。其中,初损值采用表1中的统计平均值,产流时间通过初损值除以雨强得到,流量最大值根据式(2)计算得到。根据表2,在图5中绘出不同雨强条件下的概化线性涨水过程线,可以看出,概化直线与实际涨水曲线的变化趋势基本符合。

表1 SBS下垫面降雨初损统计表
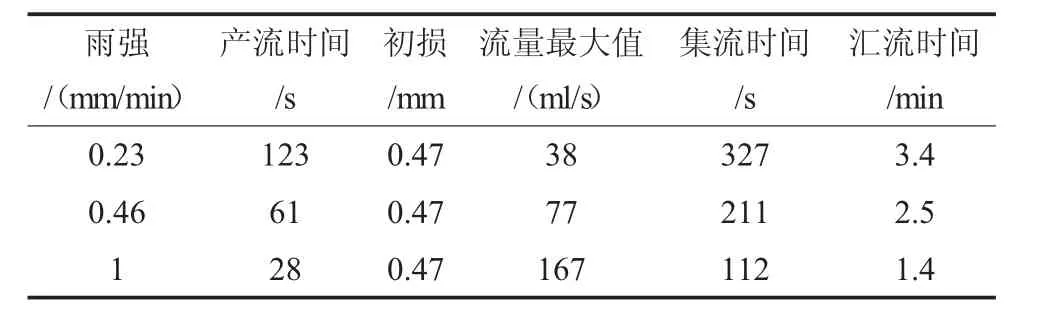
表2 SBS下垫面不同雨强条件下涨水曲线特征参数
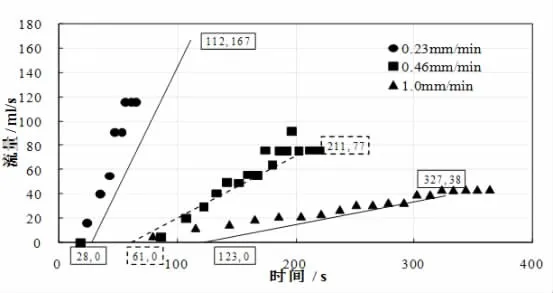
图5 SBS下垫面不同雨强条件下涨水曲线
3.2 SBS下垫面场次降雨径流系数动态模拟
根据式(9),分别模拟不同降雨历时、雨强条件下(以0.27mm/min为例)SBS下垫面场次降雨径流系数的变化规律,如图6所示。其中,考虑到试验雨强与表1中的雨强大小比较接近,坡面汇流时间近似采用表1中的数据。为便于比较,在图6中同时给出了考虑初损情况下采用Linsley公式计算得到的场次降雨径流系数变化情况。图7为不同雨强条件下场次降雨径流系数计算值与实测值的对比情况。
从图6~7可以看出:采用本文公式计算得到不同雨强条件下SBS下垫面场次雨量径流系数值与试验实测值的变化趋势基本吻合,两者数值大小基本位于45°线附近,而采用Linsley公式的计算结果在降雨历时较短时则相对偏小。

图6 场次雨量径流系数模拟结果(I=0.27mm/min)
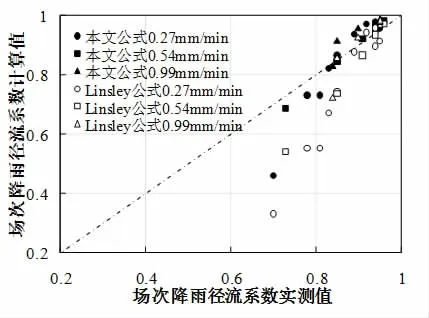
图7 场次雨量径流系数模拟值与实测值对比情况
4 结论
1)在不透水地表降雨径流过程中,由于坡面径流作用,地表蓄水量并不等于降雨量,造成地表实际填洼损失量较Linsley公式有所减小。
2)基于水量平衡原理,考虑坡面径流作用,推导建立了不透水地表降雨径流系数的计算表达式。
3)通过与他人试验结果进行比较,结果表明计算值与实测值变化趋势基本吻合,两者数值基本位于45°线附近,计算精度较Linsley公式有所提高。

