符合“欧氏几何”的洛伦兹变换图示法的设计

刘 远

(《山东财经大学学报》编辑部，山东财经大学，山东 济南 250014)

洛伦兹变换是相对论理论的重要内容，其变换公式及物理图像通常用一个光锥来表示。闵可夫斯基时空图是最常见的洛伦兹变换的图示法，邓魁英[1]通过闵可夫斯基时空图实现洛伦兹变换的几何导出。梁灿彬[2]总结这种作图方法：“要先选一个惯性系作标准(t轴和x轴分别画成竖直和水平)”，即只能有一个以直角坐标系表示的参考系，这是特殊的“闵氏几何”，魏益焕[3]验证“欧氏空间”的圆对应“闵氏空间”的双曲线。初学者往往不习惯“闵氏几何”作图，而需要借鉴其他图示法来理解洛伦兹变换，如缪劲松[4,5]介绍狭义相对论的物理现象，采用了多种示意图。

对这一问题，黄献民[6]提出将时空图画成对称的特例，党兴菊[7]设计了斜交坐标轴时空图。在此基础上，文章尝试设计符合“欧氏几何”的洛伦兹变换图示法。

1 简化洛伦兹变换

按照张元仲[8]讨论，建立有特殊设计的两惯性参考系：S′系沿S系x轴正方向以不变速度运动，两参考系在各自零时刻重合(即时空轴重合)。对两参考系，仅讨论时间和沿运动方向的空间，以x、x′表示空间坐标，使用特殊的时间坐标(单位：米)

其中t0、t′0为通常的时间。设两参考系相对速度为u，c为光速，设有角度μ，使

sinμ=u/c

可将洛伦兹变换逐步简化过程如下：

经过类似步骤，将洛伦兹变换的4个公式改写为

因其能被改写为以上几何函数形式，故可以设计符合“欧氏几何”的图示法来表示洛伦兹变换。

2 图示法的设计过程

2.1 x′=0条件下的洛伦兹变换图示法

将x′=0代入洛伦兹变换，设t′为任意值t′1，得到式(1)、式(2)

式(2)表示：当S系t时刻，S′系空间坐标零点的S系空间坐标为t×sinμ。

由以上两式，x′=0条件下，可构造x和t′1为两直角边，t为斜边的直角三角形，如图1所示。

图1 x′=0条件下的洛伦兹变换示意图

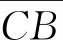
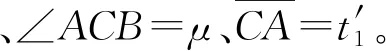
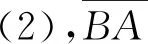
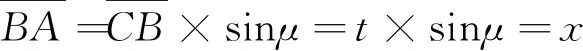
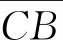
2.2 x=0条件下的洛伦兹变换图示法

将x=0代入洛伦兹变换，设t为任意值t1，得到式(3)、式(4)

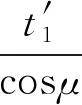
图2 x=0条件下的洛伦兹变换示意图

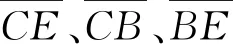
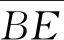
图2中三角形CBE可表示火车观察月台。按照日常生活经验，当月台上的接站人看到行驶中火车的尾端车厢里的乘客时，乘客自然也可以看到接站人，按照洛伦兹变换则不同。从洛伦兹变换，月台上的S系观察者在t1时刻，会看到火车尾端车厢的挂钟指向t′1，但这是一种单方面的观察。如果月台上的接站人此时向火车挥手，在S′系t′1时刻，火车上的乘客能看到吗？从洛伦兹变换，他不能。

2.3 一般性的洛伦兹变换图示法

设x、t为任意值(x1,t1)，代入洛伦兹变换，得到

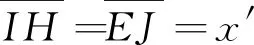
(9)

(10)

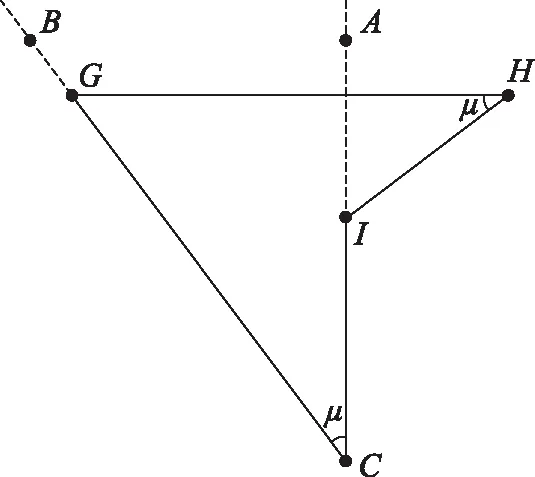
图3 一般性的洛伦兹变换图示法

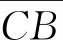
3 “异地同时性的破坏”“长度收缩”的图示法

设t′为定值t′2，代入洛伦兹变换，得到

由上式，当t′为定值t′2，x和x′一一对应，当x增大，x′也增大；x和t一一对应，当x增大，t也增大。“火车—铁轨”模型中，这相当于火车上的乘客在t′2时刻拍摄的一幅铁轨、月台和火车的照片。当照片中某节铁轨上挂钟指向t2时刻，想知道这是哪段铁轨(求x)、对应哪节车厢(求x′)，可由图4表示。

图4 定值t′2条件下，两特定事件的洛伦兹变换示意图

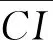
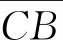
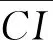
图4中，易知E和H的S′系空间坐标相同，即

因此，对E的S′系空间坐标与H′的S′系空间坐标之差，有

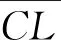
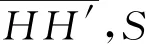
4 结语

本文设计图示法以符合“欧氏几何”的形式表示洛伦兹变换和狭义相对论的各种物理现象，可作为初学者和爱好者学习中的借鉴。最后需要指出，论文讨论的仅是一维空间、一维时间的洛伦兹变换，洛伦兹变换的核心在于变换要保持两个惯性系光速不变，因此三维空间的旋转，也是一种洛伦兹变换。更为广义的空间反射、时间反演等分立变换都可以保持光速不变，因此也都可以看做是洛伦兹变换。

论文写作和修改过程中，先后得到山东财经大学李秀荣教授、山东建筑大学郝怀杰教授、山东大学许心光教授提出的宝贵意见，以及编辑和审稿人对本文的修改意见，在此表示感谢。