微型石英音叉谐振陀螺抗冲击的建模与仿真
白 冰,赵玉龙
(西安交通大学机械制造系统工程国家重点实验室,西安710054)
0 引言
陀螺是在惯性空间中测量旋转物体角速率的传感器,在制导、探测等许多领域有着极为广泛的应用[1-2]。传统陀螺因体积大、功耗高、价格昂贵等原因,已逐渐被市场所淘汰。近年来,随着微机电系统 (Micro Electro Mechanical System,MEMS)技术的发展和微制造工艺的逐渐成熟,陀螺的小型化慢慢引起了研究人员的重视。MEMS俗称微机电机械系统[3-4],是将微传感器、微执行器和信号处理电路集成在一起的复杂的微小系统。通过MEMS技术制造的微陀螺具有体积小、质量轻、成本低、可靠性高等特点,且有着与传统陀螺相当的性能,这拓展了其应用范围。目前,微机械陀螺已成为科研机构和传感器制造公司的重点研究对象[5-6]。
微型石英音叉谐振陀螺是MEMS陀螺的一种,其石英材料具有较高的品质因数,且具有压电效应和逆压电效应,可以用于陀螺的驱动和检测。在20世纪80年代,美国的BEI Systron Donner公司是石英角速度陀螺领域的佼佼者,其产品具有较好的零偏稳定性。1993年,Charles Stark Draper实验室研制出了微机械梳齿驱动的单晶硅音叉陀螺[7]。在世界范围内,许多公司已开始生产微机械陀螺,并且产品已经投入市场。其中,BEI、ADI、Robert Bosch、Silicon Sensing在微机械陀螺领域占据了90%以上的市场份额[8]。例如,2002年,ADI公司成功研制了该公司的第一代微机械陀螺产品并将其投入市场[9]。
随着MEMS技术的飞速发展,微型石英音叉谐振陀螺在各个领域中的应用越来越广泛,传感器的工作环境也越来越复杂,有些工作环境非常恶劣,需要经受冲击环境的考验。微型石英音叉谐振陀螺在冲击环境下的可靠性会对整个系统工作的可靠性产生直接的影响。本文通过对微型石英音叉谐振陀螺的六个方向进行半正弦冲击仿真,分析了六个方向冲击对陀螺结构的应力分布,从而找到悬臂梁的厚度下限。
1 微型石英音叉谐振陀螺的工作原理
微型石英音叉谐振陀螺的工作原理如图1所示。

图1 微型石英音叉谐振陀螺的工作原理图Fig.1 Working principle diagram of micro quartz tuning fork resonant gyroscope
驱动音叉有电信号激励其在驱动模态的谐振频率点附近振动,它是一个参考振动。当音叉绕其转动轴以角速度Ω旋转时,驱动音叉受到哥氏力作用并产生垂直于音叉平面方向的振动。这个哥氏力运动由支撑梁传递到读出音叉,使读出音叉产生垂直于音叉平面的方向振动。读出音叉的敏感振动信号通过压电效应转换为电信号,电信号与输入角速度Ω成正比,该电信号通过信号调理电路就可以计算出输入角速度[10]。音叉谐振陀螺的工作原理与石英材料的机械属性和电学特性较为契合,二者结合可以设计出结构简单、便于加工、精度较高的石英音叉谐振陀螺。
2 冲击试验技术
冲击通常是指物体(或介质)同研究对象间的单次相互作用,能激起瞬态扰动的力、位移、速度或加速度的突然变化,并在很小的空间内释放出相当大的能量。冲击运动是具有明确起点和终点的非周期过程,因此,它具有确定的脉冲持续时间[11]。
在冲击环境试验中,最常见的类型为半正弦波脉冲波形,其波形图如图2所示,其数学表达式为

式(1)中,ü0为半正弦波形的峰值,D为波形持续时间。

图2 半正弦波脉冲波形图Fig.2 Waveform of half sinusoidal wave pulse
在实际情况中,当冲击脉冲作用在传感器后,初始阶段会产生类似半正弦波脉冲波形的近似波形。但这个过程不会立刻消失,接下来还会产生一系列的衰减振荡波形,之后波形才会逐渐消失。这个过程很难用某一个数学表达式进行表达,通常,需要将冲击运动在时间域的表达式转换成频率域,即对冲击函数进行Fourier变换。假设冲击函数为),其Fourier变换为
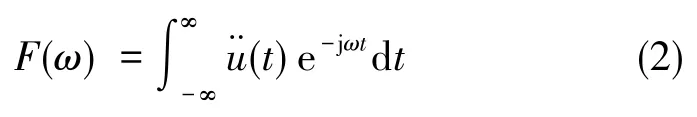
当冲击函数为半正弦脉冲时,其频谱图如图3所示。经Fourier变换后的频谱函数为


图3 半正弦脉冲频谱图Fig.3 Spectrum of half sinusoidal pulse
冲击响应谱是工程中广泛应用的重要概念,简称冲击谱[11]。冲击谱是对设备实施抗冲击设计的分析基础,也是控制产品冲击环境模拟实验的基本参数。所谓冲击谱,是指冲击源施加于一系列线性、单自由度的质量-弹簧系统时,将各单自由度系统的响应运动中的最大响应值作为对应于系统固有频率的函数而绘制的曲线。
冲击响应谱可通过试验测得,也可以通过计算求出。图4是国家标准的冲击试验方法中给出的无阻尼单自由度线性系统的半正弦波冲击响应谱。

图4 50g、11ms的半正弦脉冲的冲击响应谱Fig.4 Shock response spectrum of 50g,11ms half sinusoidal pulse
图4给出的是幅值A为50g、持续时间D为11ms的半正弦波冲击响应谱,同样也给出了归一化的坐标表示冲击响应谱。通过归一化的坐标冲击响应谱可以换算出其他情况的半正弦冲击响应谱,换算公式为

式(4)中,amax为加速度最大响应值,A为激励脉冲幅值,D为脉冲持续时间,fn为单自由度系统的固有频率。
3 COMSOL Multiphsics建模与仿真分析
3.1 仿真模型的建立
对于石英音叉谐振陀螺抗冲击设计,关键在于其锚点与振动单元连接的 “V”字梁结构,如图5所示。“V”字梁结构的厚度决定了音叉陀螺的各阶频差和敏感结构的抗冲击能力。根据微型石英音叉谐振陀螺的实际工作环境,其随机振动的频率为20Hz~2500Hz,必须保证在驱动模态的频率叠加了±2500Hz以后的频率范围内不能有除检测模态频率的其他模态频率点的存在。经过分析仿真,得到了其 “V”字梁的宽度为200μm,厚度的上限为100μm。
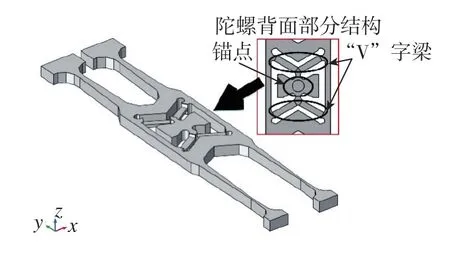
图5 微型石英音叉谐振陀螺的结构示意图Fig.5 Structure schematic diagram of micro quartz tuning fork resonant gyroscope
利用有限元分析软件建立的陀螺敏感部件模型如图5所示。在进行冲击仿真之前,需要先对该敏感部件进行模态分析,找到在相应的冲击响应谱频率分析范围内存在的前几阶振动模态的振动频率,然后再对陀螺敏感部件进行六个方向的冲击仿真,如图6所示。冲击脉冲为幅值为1500g、持续时间为2ms的半正弦波,其函数为

根据归一化的冲击响应谱,可以换算出上述半正弦波函数冲击响应谱的amax和fn,具体为
式(6)中,amax,1500g和fn,1500g分别为该冲击下的加速度最大响应值和其所对应的单自由度系统的固有频率。根据归一化冲击谱函数的换算,得到上述半正弦波函数的冲击响应谱如图7所示。
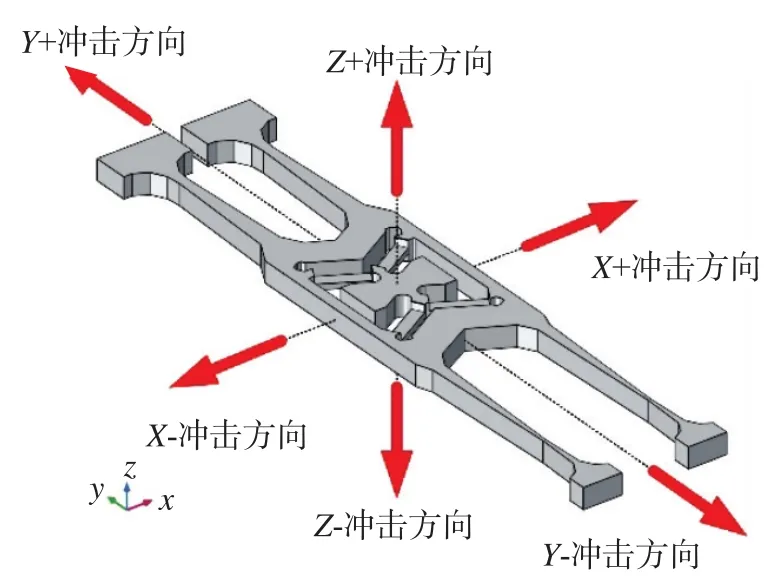
图6 冲击仿真的六个方向Fig.6 Six directions of shock simulation
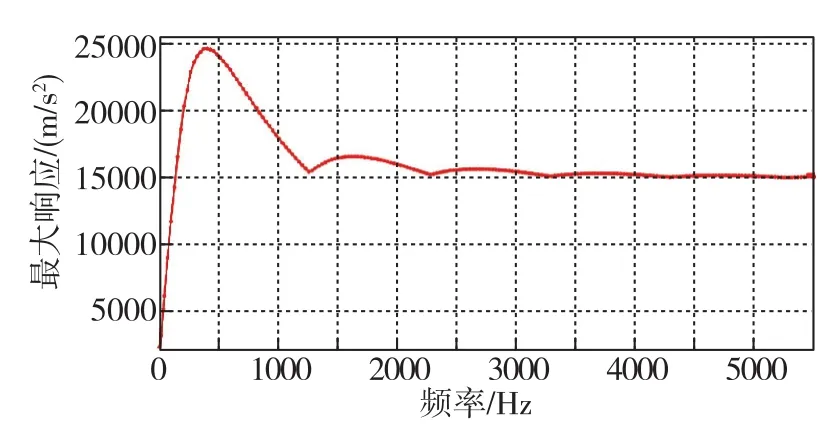
图7 幅值为1500g、持续时间为2ms的半正弦波的冲击响应谱Fig.7 Shock response spectrum of a half sinusoidal wave with amplitude of 1500g and duration of 2ms
3.2 仿真结果和分析
(1)模态结果分析
由图7可以看出,给定的冲击响应谱的频率范围为0Hz~5500Hz,通过对微型石英音叉谐振陀螺进行模态分析,得到不同 “V”字梁厚度的陀螺结构在该频率范围内的前几阶模态频率,如表1所示。将这些频率点对应在冲击响应谱图中,如图8所示。从图8(a)可以看出,梁厚为100μm时,前三阶模态的频率点在0Hz~5500Hz范围内;从图8(b)可以看出,梁厚为60μm时,前四阶模态的频率点在0Hz~5500Hz范围内。这说明在收到相同冲击时,后者更易产生较大的结构应力。
(2)冲击结果分析
利用1500g、2ms的半正弦冲击脉冲的冲击响应谱, 对不同厚度点(60μm、65μm、70μm、75μm、80μm、85μm、90μm、95μm、100μm)的“V”字梁的陀螺结构进行六个方向的仿真分析,得到在该半正弦冲击响应谱的应力分布。

表1 不同 “V”字梁厚度结构的前几阶模态频率Table 1 Modal frequencies of different V-shaped beam thickness structures

图8 不同梁厚结构的频率点在冲击响应谱中的位置Fig.8 Position of the frequency points of different beam thickness structures in the shock response spectrum
梁厚为100μm时,受到六个方向的指定冲击后,产生的结构形变和应力分布如图9所示。从图9(a)和图9(b)中可以看出, 当受到X方向的冲击时,检测音叉较细部分的应力较大,且 “V”字梁和锚点连接处的应力较大;从图9(c)和图9(d)中可以看出,当结构受到Y方向的冲击时,其产生的应力比其他两个方向冲击产生的应力小;从图9(e)和图9(f)中可以看出, 当受到Z方向的冲击时,“V”字梁和锚点连接处的应力最大,更容易产生断裂。
梁厚为60μm时,受到六个方向的指定冲击后,产生的结构形变和应力分布如图10所示。从整体来看,梁厚为60μm时受到指定冲击后产生应力比100μm时产生的应力明显增大,更容易产生断裂。

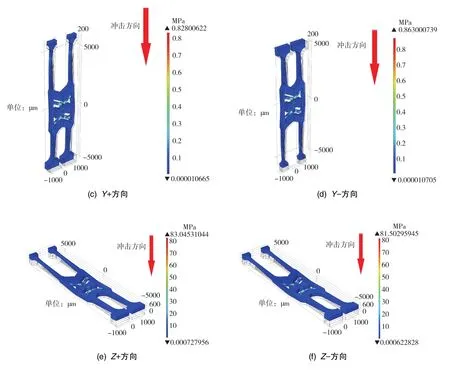
图9 “V”字梁厚度为100μm时的六个冲击的应力和形变Fig.9 Stress and deformation of six shocks when V-shaped beam thickness is 100μm


图10 “V”字梁厚度为60μm时的六个冲击的应力和形变Fig.10 Stress and deformation of sixs hocks when V-shaped beam thickness is 60μm
“V”字梁厚度的所有数据点在受到六个方向的冲击响应谱冲击时的体应力最大值如表2所示。可以看出,当 “V”字梁厚度为100μm时,其受到Z+方向的冲击产生的应力最大,为83.045MPa;当 “V”字梁厚度为60μm时,其受到Z-方向的冲击产生的应力最大,为149.032MPa;当 “V”字梁厚度为80μm时,其受到Z-方向的冲击产生的应力最大,为 94.721MPa;当 “V”字梁厚度为75μm时,其受到Z-方向的冲击产生的应力最大,为100.512MPa。由于石英材料的断裂强度为95MPa,所以 “V”字梁的厚度最小值约为80μm。
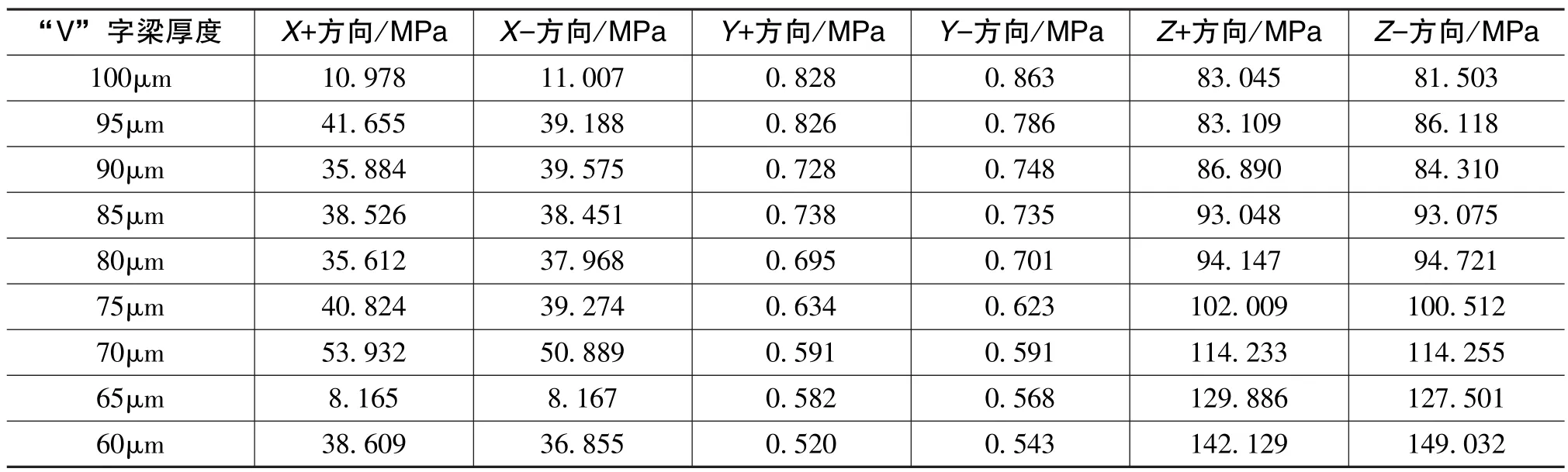
表2 “V”字梁厚度的所有数据点在受到六个方向的冲击响应谱冲击时的应力最大值Table 2 Maximum stress at all data points of the V-shaped beam thickness subjected to shock response spectra in six directions
4 结论
随着陀螺的迅速发展,其应用领域越来越广,应用环境也越来越多样,冲击环境是其中一个,日益受到关注。当 “V”字梁厚度变化时,传感器的驱动模态的频率和抗冲击性能均会发生变化。因此,本文通过对微型石英音叉谐振陀螺抗冲击能力的建模和仿真,得出了在受到六个方向的幅值为1500g、持续时间为2ms的半正弦波冲击时,不同 “V”字梁结构的微型石英音叉谐振陀螺产生的应力分布。当 “V”字梁的厚度最小值为80μm时,传感器能经受指定的冲击信号,这对陀螺的其他参数具有一定的参考意义。

