基于PI+重复控制的三相四桥臂有源电力滤波器的研究

(1.石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043；2.衡水铁路电气化学校，河北 衡水 053000；3.中铁建电气化局集团北方工程有限公司，山西 太原 030053；4.建投承德热电有限责任公司，河北 承德 067000)

0 引言

随着电力电子技术的快速发展，电力电子设备和非线性、冲击性负荷的广泛运用，造成电力系统谐波污染日趋严重，谐波治理也变得越来越重要。 目前，应用比较多的电流环控制算法主要有PI控制、无差拍控制、重复控制等。针对不同的控制要求，每种控制方法应用场合以及实现的效果也不同。 杨新华等[1]使用PI控制，此种控制算法原理简单、便于理解，但属于有差调节、易受带宽限制，稳态精度不高。朱建玉等[2]使用无差拍控制，此方法能快速跟踪电流变化，提高控制速度。但是存在计算量较大、响应精度和稳定性较差的缺陷。魏阳超等[3]使用重复控制，此方法原理较简单，应用时稳定性较好，但重复控制动态响应速度不高。还有文献使用滑模控制，此控制方法鲁棒性强，动态响应快，但是存在控制精度不高的弊端，且易使系统发生颤动，针对此问题张琛[4]提出了一种基于全程滑模变结构控制的有源电力滤波器，将全程滑模变结构控制方法应用到有源电力滤波器控制系统中，实现了减小系统抖振的功能。综合不同控制算法的优缺点，最终选用了PI+重复控制的复合控制方式，以便达到更好的谐波补偿效果。

1 有源电力滤波器的结构设计

图1所示为三相四桥臂有源电力滤波器(APF)的拓扑结构图，根据基尔霍夫电压和电流定律可以得到在abc坐标系下的表达式，为了计算方便，经Park变换将其转为dp0坐标系表达式，并得到如图2所示的数学模型框图。

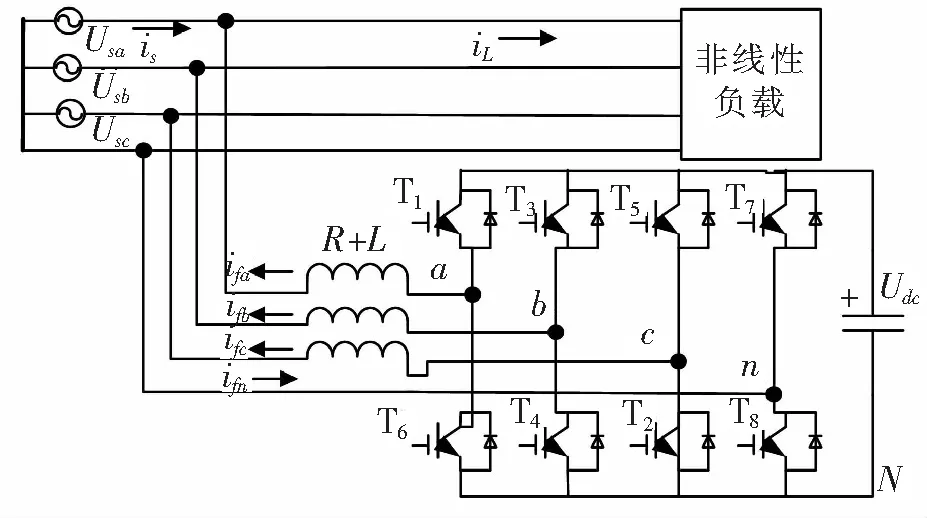
图1 三相四桥臂APF拓扑结构

图2 APF在dq0坐标系下数学模型框图

分析图2发现，四桥臂APF在d轴和q轴通道存在相互耦合关系，因此需要进行解耦控制实现各轴独立控制[5-6],最终得到图3所示的三相四线制有源滤波器在dq0坐标系下的整体控制结构图。观察发现要实现APF谐波补偿功能，系统设计分多个重要模块，包括谐波电流检测、电流环控制、电压环控制和PWM调制等。在谐波电流检测选用优化瞬时无功检测法、PWM调整选3D-SVPWM的基础上对电流控制进行分析。

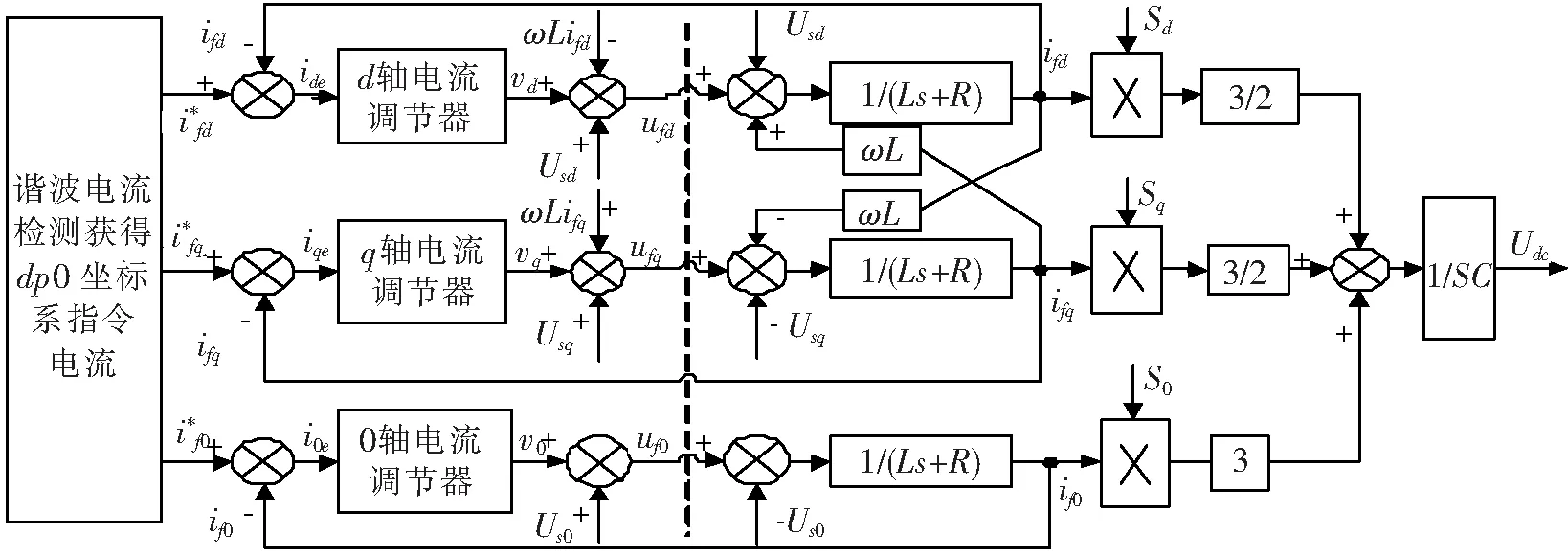
图3 三相四线制APF在dq0坐标系下整体控制结构图

2 电流环控制

电流环控制在选用传统PI控制方式时，虽然动态响应速度较快，但存在稳态精度不高的缺点，使控制效果不理想[7]。因此，为了弥补PI控制的不足，将其与重复控制并联使用。因为在使用重复控制时，虽然其动态响应速度不高，但是其稳态输出精度较高。如果将两者结合使用，可以很好地弥补各自单独控制的不足，从而实现电流环控制的要求。

2.1 重复控制器的结构

重复控制是利用内模原理进行控制，其中最根本的部分就是它的内模结构，主要作用是为控制系统提供稳定的控制信号[8]。图4即重复控制内模结构框图。

Q(z)可以设计为一个低通滤波器，实际应用时Q(z)一般取0.95～1之间的常数。而整体的重复控制系统结构框图如图5所示。

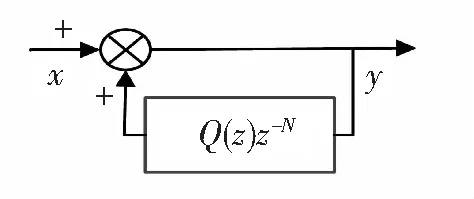
图4 重复控制器的内模结构

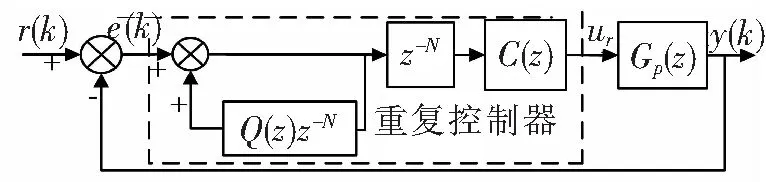
图5 重复控制系统框图

重复控制系统框图主要包括以下几个部分：重复信号发生器即重复内模结构、周期延迟环节z-N、补偿器C(z)等，其中C(z)=KrzkS(z)。而控制系统中的被控对象为Gp(z)，控制器的输出为ur[9-10]。其中，周期延迟环节z-N在系统控制中，能使指令信号经过一个基波周期的延迟之后输到被控对象，从而使得超前环节的设置成为可能。补偿器C(z)在控制系统中，主要目的是对被控对象Gp(z)给予幅值和相位2个方面的补偿。其中Kr为比例因子，主要目的是保证系统在中高频率中的稳定。zk作为超前环节，主要目的是对被控对象提供相位补偿。S(z)一般被设计成为二阶低通滤波器，维持系统的稳定性。

2.2 复合控制器参数设计

本文使用的复合控制是PI控制与重复控制器并联组合的控制系统，两者的组合可以弥补任意一种控制方式的不足，从而在保证控制系统稳定的前提下，又能保障控制系统的动态响应特性。复合控制系统的结构框图如图6所示。对于复合控制参数设计主要分以下几部分。

图6 复合控制系统框图

2.2.1 被控对象的离散化处理

本系统的被控对象可以看作一阶惯性环节，其传递函数可表示为

(1)

将被控对象离散化，只需要在此被控对象前面串联一个零阶保持器即可[11]。

因此，被控对象经过零阶保持器后得到z域下的脉冲传递函数为

(2)

且采样频率为10 kHz，L=2.5 mH，R=0.1 Ω，将参数代入式(2)，可得

(3)

由此可见，被控对象的特征根位于单位圆内，从而说明系统是稳定的。

2.2.2 PI控制器参数设计

对于PI控制器的设计主要是保证在系统稳定的前提下，选择合适的控制参数。在d、q、0坐标轴下的控制器参数设计，可以以d轴为例，确定复合控制中的PI参数。s域下的PI控制系统模型如图7所示。

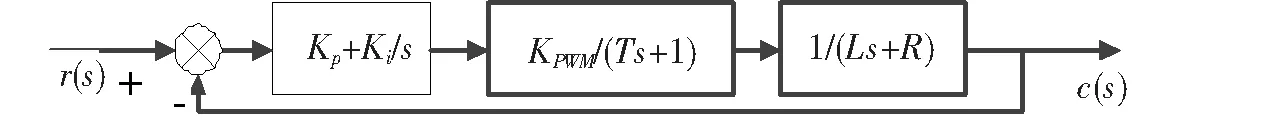
图7 s域下PI控制系统模型

此模型KPWM为调制增益，最终取值为1。因此可得此控制系统开环传递函数为

(4)

将公式(4)进行变换，可以写成零极点的形式，可以表示为

(5)

如果使用零极点对消的原则，将此系统的开环表达式改写成二阶系统，可以令Ki/Kp=R/L。因此，此时得到的开环传递函数为

(6)

根据开环传递函数也可以推导出此系统的闭环传递函数为

(7)

而作为典型的二阶系统的传统函数式

(8)

为了获得很好的动态性能，令ζ=0.707。使闭环传递函数式(7)和典型的二阶系统传递函数式(8)相等，可以计算得到参数Kp=2.50、Ki=500。所以，PI控制在s域中的传递函数为

(9)

然后，将其转换到z域则可以得到脉冲传递函数为

(10)

2.2.3 重复控制器参数设计

关于重复控制器设计也需要确定其在本系统中的参数值。设计中的基波频率为50 Hz，开关频率fs=10 kHz。

(1)周期延迟环节中系数N的确定。由于，N为采样频率和基波频率的比值。因此，可以得到系统中N取200。

(2)内模补偿环节Q(z)的确定。Q(z)一般取值范围在0.95～1之间。而通过仿真验证，当Q(z)取值为0.96时，仿真效果良好，所以Q(z)最终取0.96。

(3)补偿器C(z)的确定。关于补偿器设计部分，重要的是确定S(z)二阶低通滤波器，它的作用是提高系统的稳定性。设计此滤波器时，选取的截止频率fc太大，会使系统稳定性减小，失去原有设计目的；如果选取截止频率fc太小，会降低系统输出高频谐波能力，使APF补偿所需谐波功能不能很好实现[12]。通过对实际APF功能分析，确定滤波器设计时需补偿30次以下的谐波，即补偿器设计时的截止频率不能低于30次以下的谐波频率。最终选取截止频率为2 000 Hz。

C(z)表达式中最重要的低通滤波器S(z)的确定式通过Matlab工具包中的FDATool分析工具实现，此工具是在Simulink路径下获得的。S(z)采用了二阶巴特沃斯低通滤波器，并根据设定的截止频率和采样频率等参数，得到此滤波器的幅频、相频以及群延时曲线。并且通过查看设计的滤波器系数，最终得到了二阶低通滤波器S(z)的脉冲传递函数为

(11)

图8为得到的S(z)滤波器的幅相频特性曲线以及群延时特性曲线。

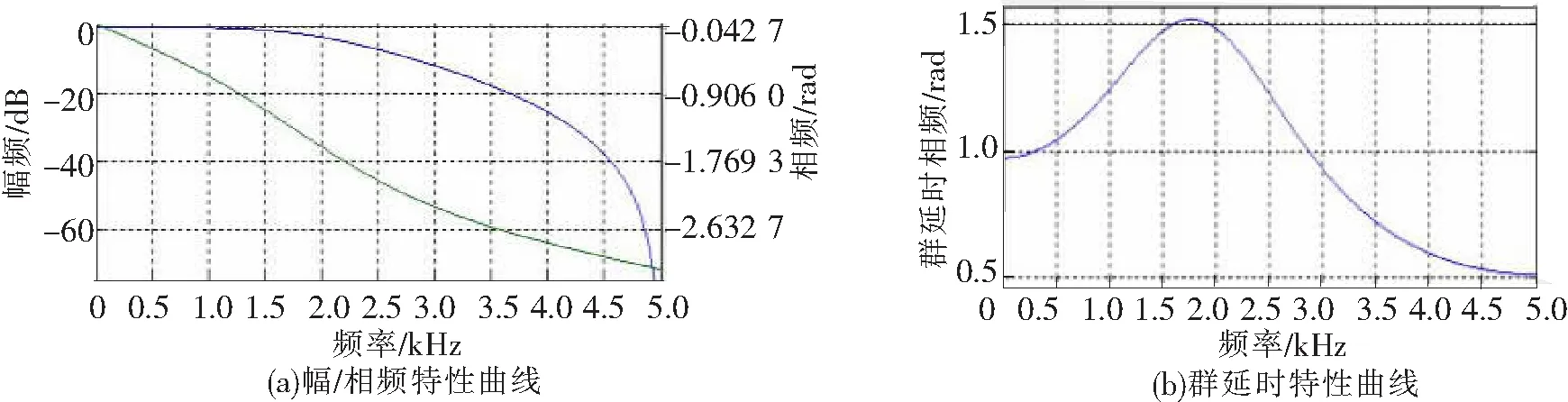
图8 补偿器S(z)的特性曲线

通过分析S(z)的特性曲线，在中低频率内延时大约一个周期，也就是补偿器的使用使得相位滞后一拍，又因为数字滤波器的一拍滞后，使得总延时为两拍，最终确定超前环节的系数k取值为2。又根据系统稳定的要求，增益Kr取值为0.5。将上述复合控制器的参数确定后，就可以确定复合控制系统开环传递函数，然后确定特征表达式，当所有的特征根全部位于单位圆内，就能确定系统的稳定性，实现复合控制的功能。

3 仿真对比分析

3.1 整体仿真模型搭建

本系统的仿真参数：电源为三相220 V交流电源，频率50 Hz；负载为三相不可控整流桥带RL负载，且B相又连接了一个单相带RL负载的整流桥；开关频率为10 kHz；直流侧电压为700 V；输出电感L取1.5 mH；直流侧电容为4 500 μF。图9所示是APF整体的仿真模型。

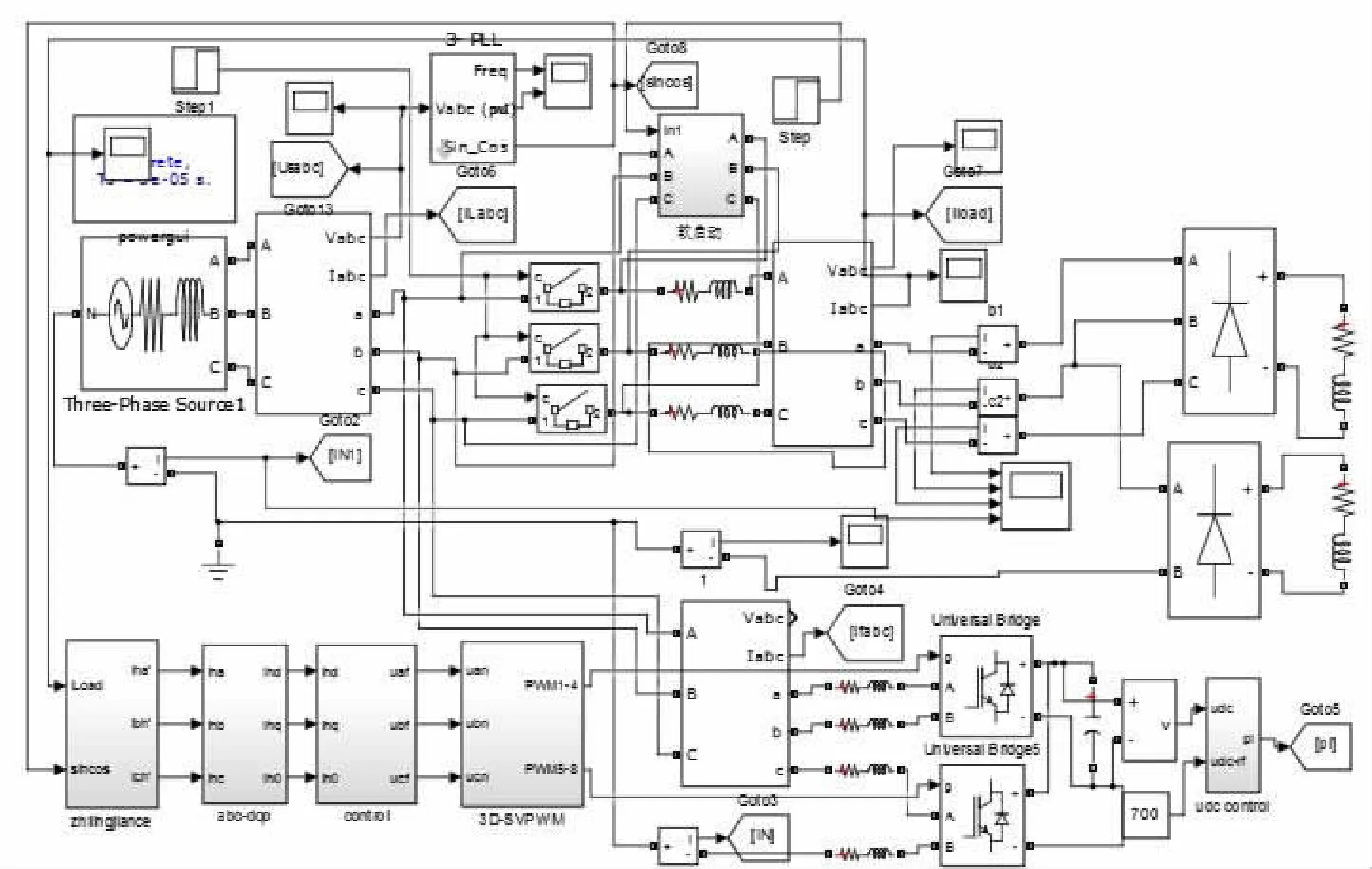
图9 三相四桥臂APF整体仿真模型

3.2 单独PI控制仿真分析

确定了系统整体仿真模型之后，需要通过仿真的方式验证PI+重复控制的复合控制方式与传统的PI控制的仿真效果的区别。本节谐波源仍为三相不平衡负载，便于对比分析，仿真过程仅改变控制方式，其余条件均不变。在电流环使用PI控制时，通过仿真得到三相负载电流波形，如图10所示。通过观察得到，补偿前三相负载电流严重不平衡。当加入补偿装置后，在电流环PI控制的基础上得到补偿后网侧电流波形，如图11所示。

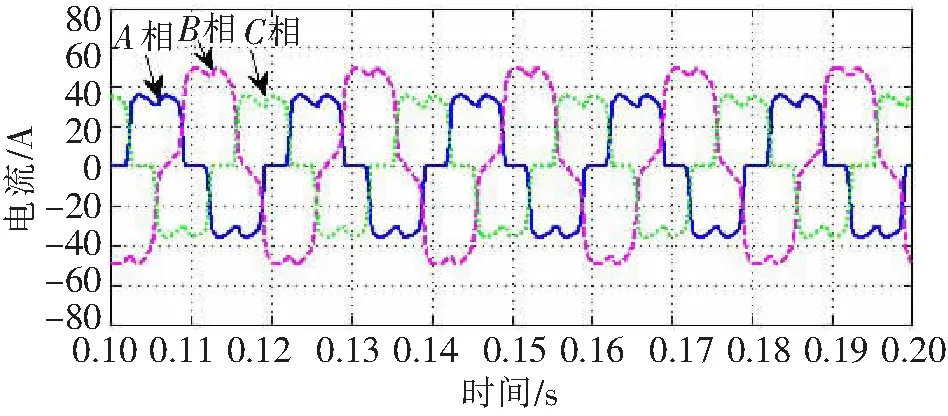
图10 三相负载电流波形

图11 补偿后网侧电流波形

由图10、图11可得，补偿前负载电流严重不平衡，补偿后三相电流基本平衡，但在负载电流突变点处，补偿后的电流存在严重的尖冲电流，为了具体分析补偿效果，以A相为例，通过频谱分析可以得到其补偿前后负载侧和网侧的电流频谱分析图，如图12所示。

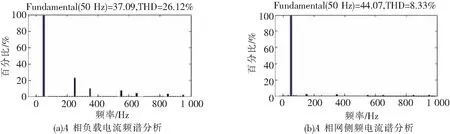
图12 单独PI控制时的A相频谱分析

由图10、图11和图12可得，补偿前A相负载电流畸变率为26.12%，补偿后为8.33%，补偿前三相负载电流严重不平衡，补偿后三相电流基本平衡，可以实现补偿三相不平衡谐波电流的目的，只是补偿后的谐波含量未达国家标准水平(THD<5%)的要求。且在负载电流突变即换流点处，补偿后电流存在较大的“尖冲”。存在这种现象是因为单独PI控制方式的局限性，使得控制器的带宽有限，从而产生了“尖冲”电流现象，对此可以考虑将重复控制器和PI控制器并联使用，以增大电流环的带宽，间接抑制负载突变点处带来的“尖冲”电流。

3.3 PI+重复控制仿真分析

图13为电流环使用PI+重复控制的复合控制时仿真模型。在此控制下，最终可以得到补偿后的网侧电流波形如图14所示。A相负载电流和补偿后网侧电流频谱分析如图15所示。

图13 PI+重复控制的仿真模型

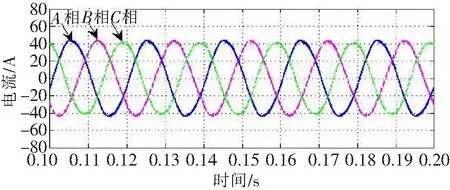
图14 补偿后网侧电流波形

图15 复合控制时A相频谱分析

由图14和图15可得，补偿后三相电流基本平衡，且以A相为例，负载畸变率由26.12%，降到网侧畸变率3.24%，补偿后电流不再存在“尖冲”现象。因此，在其它条件相同的前提下，综合对比分析3.2节和3.3节的仿真结果，可得：使用单独PI控制时，补偿前负载严重不平衡，补偿后虽然也能实现补偿三相不平衡电流的目的，但在负载电流换流处，补偿后网侧存在较大的“尖冲”，且补偿后谐波畸变率为8.33%，高于国家标准(THD<5%)。而使用复合控制时，在负载电流换流点处，补偿后网侧电流不再存在“尖冲”。同时谐波畸变率也由单PI控制时的8.33%降为3.24%，明显比前者补偿效果好，能满足国家标准(THD<5%)。最终选择了重复控制作为电流环的控制方式。

4 结论

为了确定三相四桥臂有源电力滤波器的电流环控制算法，从PI控制和重复控制的原理、结构、不同控制方式的优缺点出发，通过搭建仿真模型，分析电流环使用单独PI控制和PI+重复控制的复合控制方式仿真效果，经过验证，使用复合控制方式不仅提高了系统的动态特性，还大大提高了系统的稳态精度，使得谐波补偿效果较为理想，从而确定了三相四桥臂有源电力滤波器的电流环使用PI+重复控制的复合方式，也证明了该方案在理论上具有可行性，为更深一步的研究及实际应用提供了参考和依据。