高速列车气动噪声的实验模型研究
亢佳贺,刘晓日,*,王儒枭,胡佳岑,秦博,黎苏
(1.河北工业大学能源与环境工程学院,天津300401;2.象限空间(天津)科技有限公司,天津301701)
0 引言
高速列车的运行速度越来越快,气动噪声的影响更加突出,文献[1]通过不同车速下列车模型的噪声云图,表明列车表面气动噪声随车速的增加而增加[1]。有关研究[2-4]表明,随着车速的增加,各类噪声呈指数倍增长,气动噪声与车速的6次方成正比,动力系统噪声和轮轨等机械噪声分别与车速的1次方和3次方成正比。高速列车附近的最大动压随着长度的增加逐渐减小,在模型表面设置的数值仿真监测点呈随机震荡,进行傅里叶变换之后,声压幅值随着频率的增大而逐渐减小[5]。
声学探究多数依靠测量声压,环境对声压的测量结果影响很大,环境改变时测量结果会出现很大的偏差,因此要得出准确的测量结果,通常需要寻找和建立特殊的声学环境,这无疑增加了试验的难度,使试验效率大幅度降低。
互谱法测量声强不受自由场和远场条件的限制,不需要消声室,使试验更加方便快捷,能够在现场测量机器的噪声,因而广泛应用于工程实践。
本文中采用互谱声压法,即间接法(P-P法)对声强进行测量[6]。设计并搭建高速列车风洞试验台,对1:1参考模型和1:87微缩模型的雷诺数估算、相似性原则和试验中的相似条件进行对比,确定微缩模型实验的合理性;对高速列车外部的气动噪声进行仿真分析,得出表面气动噪声分布;对高速列车的噪声进行试验分析,试验测量列车在不同风速下的噪声,结合计算结果分析不同工况下的噪声和分布。
1 建模
1.1 高速列车微缩模型
探究高速列车的气动噪声需要借助风洞试验,但是通过风洞对实际的高速列车测量难度较大,实践中通常是对按一定比例缩小的模型进行研究。本文中探索1:87微缩模型的合理性,取代实际的高速列车对微缩模型展开研究。
1.1.1 参考模型和微缩模型
以比例1:1的CRH 380A高铁列车空气动力噪声试验台为参考模型[7],开展1:87微缩模型高铁列车空气动力噪声试验台的研制。建立1:87模型和参考模型的数据,证明1:87模型的合理性,为微缩模型研究的应用提供帮助。
1.1.2 雷诺数估算
1)参考模型
由于风来自风洞模型的前方,属前方风流问题,列车头部的高度和宽度相似,类似于圆柱,雷诺数
(1)
式中:D为特征长度(车头宽度),取D=3.38 m;v为速度,取v=380 km/h;t为放置模型环境温度,取t=20 ℃,γ为运动黏度,取γ= 15.7 × 10-6m2/s。
计算得出1:1模型的雷诺数Re=3.57 × 108。
2)1:87模型
1:87模型中的D相当于把1:1模型中的D缩小为1/87,其余条件没有改变,所以得出的1:87模型的雷诺数:Re1:87=4.1×106。
2个模型的雷诺数全部大于绕流场自模区[8]的雷诺数下限3×106,因此可以认为2个模型都已经进入自模区。当二者湍流强度足够大并且都大于下限时,二者不需要满足雷诺数Re相等,只需要满足几何相似就可以自动实现阻力相似。高铁列车气动噪声主要由高速的风阻和车体表面的压力波冲击产生,因此,满足阻力相似可以大大增加模型的相似性。
1.2 风洞试验段
由几何相似可以得出,列车模型l2=86.4 cm,水力直径
(2)
式中:S0为管道断面面积;C为断面周长;r为断面半径。

图1 试验段
因为试验段管道选择了圆形管道(如图1),所以它的水力直径和管道的直径相等,列车模型高度为4.7 cm,传感器距列车上表面1.5 cm,试验段口径D0为11 cm,试验段长度为110 cm。
高铁模型到试验段前端距离[9]
l1=(0.25~0.50)D0。
(3)
高铁模型到试验段后端距离[8]
l3=(0.75~1.25)D0。
(4)
取l1=0.25D0=2.75 cm,l3=0.75D0=8.25 cm,得到试验段总长
L=l1+l2+l3=97.4 cm。
(5)
1.3 风洞收缩段
为了确定收缩段的最优效果,比较了3种收缩曲线计算方法[10]:Witozinsky曲线法、五次曲线法和双三次曲线法,如图2所示。分析图中3个曲线的变化趋势,可以看出五次曲线变化比较均匀,可以让气流更均匀的通过收缩段,能够满足收缩段的设计要求。因此风洞收缩段设计采用五次曲线方法。受加工能力的限制,本文中设计成锥形管,如图3所示。
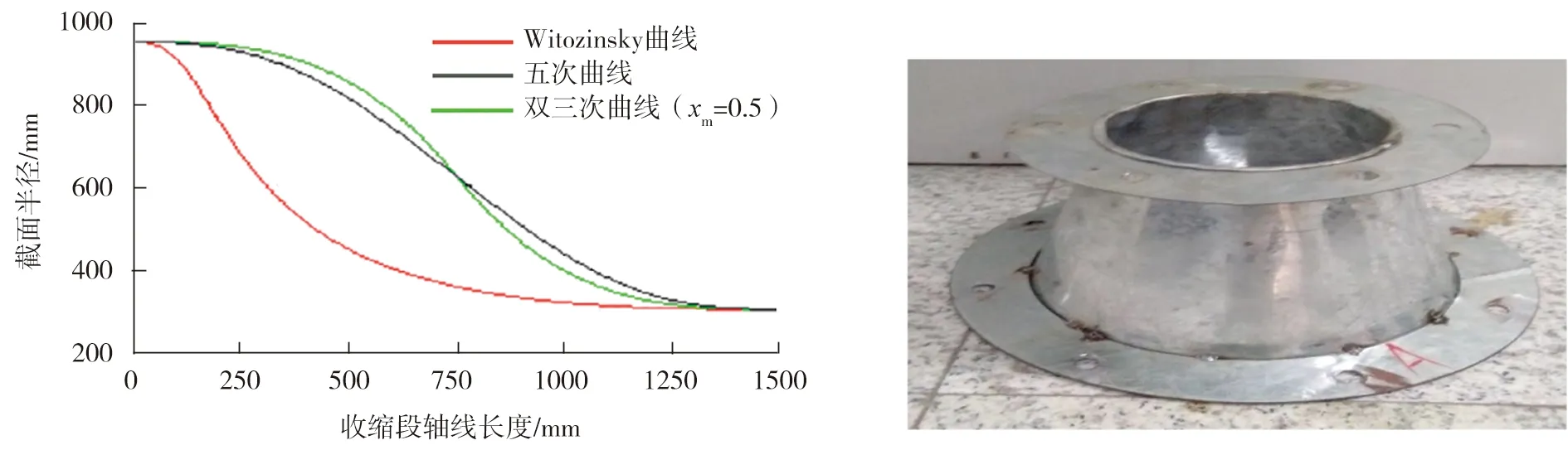
图2 收缩曲线比较 图3 风洞收缩段
由于收缩比大都在5~10[11],考虑到设计收缩段的加工问题,不能选择很大的收缩比,因此选收缩比r=5,设收缩段进口断面面积为s1,进口直径D1,应使收缩比满足
(6)

图4 风洞稳定段
1.4 风洞稳定段
稳定段直径等于收缩段进口直径,D3=D1=24 cm,取稳定段的长度为直径的1.0倍,L3=24 cm。稳定段所采用的是风机软连接的方式,如图4所示。
1.5 风洞模型整体构造
除风洞试验段、收缩段、稳定段外,风洞模型还包括蜂窝器、风机、三向风机控制器等设备,试验所用的风洞试验台如图5所示。
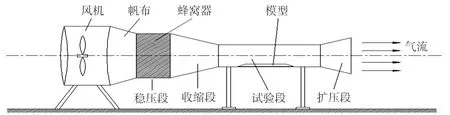
图5 风洞试验台示意图
2 试验计算与仿真模拟
2.1 试验过程
选择P-P法进行试验,用2个相距很近的声压传感器测出2个点的声压,再通过计算2个声压的互谱取其虚部即可得出该点的声强,也叫做双传声器法。由于试验台的风机、电机发出的电磁噪声和风扇发出的气动噪声将会影响试验结果,采用声压法进行测量可减少背景噪声的影响。本文中用的声压探头型号为KSI-308A213,2个传声器之间的相位差是双传声器声压探头的一个重要指标,理想的2个声压探头的传声器之间应该没有相位差,否则测量时会产生声压的严重相位误差,造成试验数据不准确。
1)搭建试验台。将风洞的稳定段、收缩段、试验段、扩张段分别用8号螺栓连接,各部分之间用橡胶垫结合,目的是增加系统的气密性,减少气流损失。再用抱箍将风洞模型固定在支架上,支架用滑动螺栓与轨道固定,使整个系统更加稳定。
2)调整风机。因为风机有支架,风机的轴线与风洞的轴线不同心,因此,把风机的支架卸下来,用几个斜面的铁支座将风机固定,调整铁支座使风机的轴心与风洞的轴心重合。通过测量,整个装置的轴线距离地面为43 cm。
3)固定传感器。将2个传感器用铁丝固定在方形木条上,传感器间距为5 cm,将木条插入在试验段打好的圆孔中并固定,探头底面距列车模型上表面1.5 cm。
4)测量噪声。通过DEWESoft X2软件测出声压数据,并输出成Excel文件,将声压数据文件导入MATLAB中,通过快速傅里叶变换(fast Fourier transtorm,FFT)得到复数F(P1),取复数F(P1)的共轭复数F*(P1),再将测得的声压P2输入到MATLAB中,通过FFT变换得到复数F(P2),计算声压信号P1和P2的互功率谱G12=(F*(P1)·F(P2))/2,取G12的虚部得到Im,将试验测得的时间和声压P的数据输入origin软件中,通过FFT变换得到声强级,利用ω=2πf计算出ω,利用I=-Im/(ρdω)(其中ρ为空气密度;d为两测点间的距离;ω为圆频率)计算出声强I,通过L=10·lg(I/I0)算出声强级,将声强级和频率数据导入origin中,得到声强级和频率的曲线,见图6。
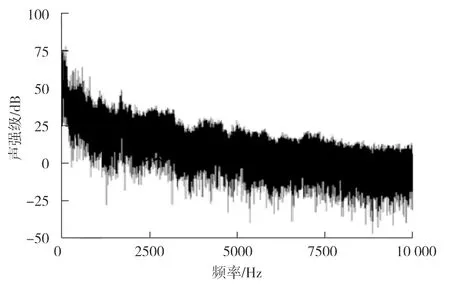
图6 36 km/h时的频谱分布
2.2 仿真模拟
高速列车大致由车头和几节车厢组成,为了简化物理模型,将高速列车模型简化为一个车头、一节车厢和一个尾车共3部分构成。高铁模型采用CRH380A,车长78 m,车宽左右距中轴线均为1.69 m,高3.7 m,车头为流线型,车头长度为12 m,车头整体离地面0.376 m。通过fluent软件仿真得出风速为36、350、400、500 km/h时的频谱图和倍频程的等效A声级分布。
风速为36 km/h时频率-声压级分布见图7。频率为0~2000 Hz时,声压级随频率的升高有下降的趋势,在低频范围内声压级较大,在高频范围内声压级很小。风速为36 km/h时倍频程的等效A声级分布见图8。由图8可知,风速为36 km/h时在250 Hz附近出现峰值,该频率成分的噪声对总噪声有较大贡献,说明该频率成分的噪声也是气动总噪声的主要组成部分,噪声能量主要集中在低频区。
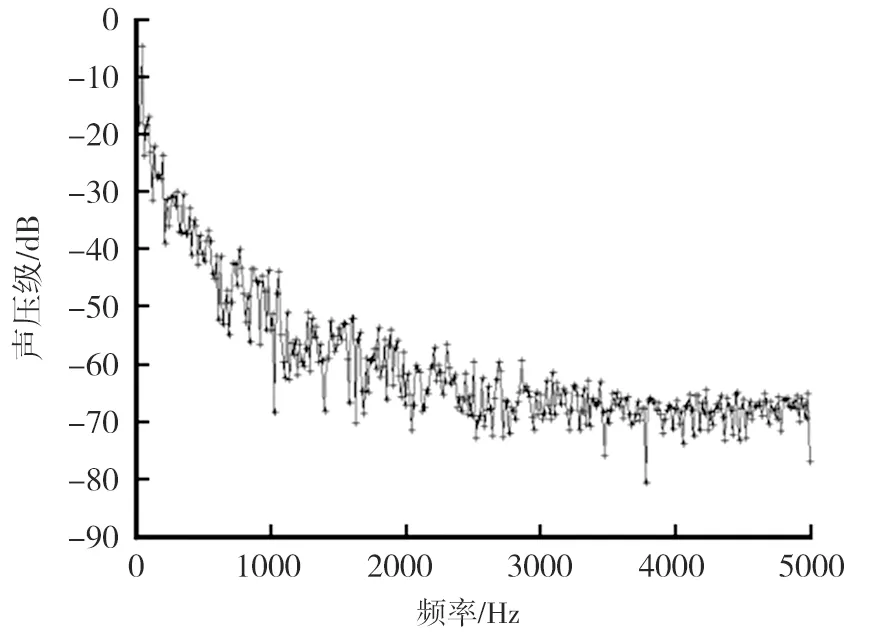
图7 36 km/h时频率-声压级分布
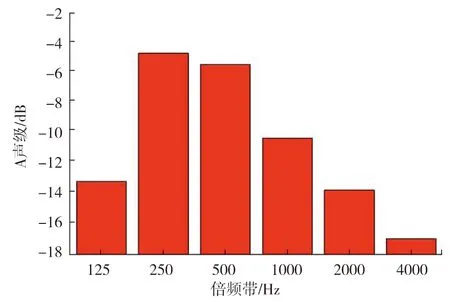
图8 36 km/h时倍频程的等效A声级分布
风速为350 km/h时频率-声压级分布见图9。频率为0~5000 Hz时,声压级随频率的升高有下降的趋势,且趋势较缓,在低频范围内声压较大,在高频范围内声压很小。风速为350 km/h下的倍频程的等效A声级分布见图10。由图10可知,风速为350 km/h时在250 Hz附近出现峰值,该频率成分的噪声对总噪声有较大贡献,说明该频率成分的噪声也是气动总噪声的主要组成部分,噪声能量主要集中在低频区。
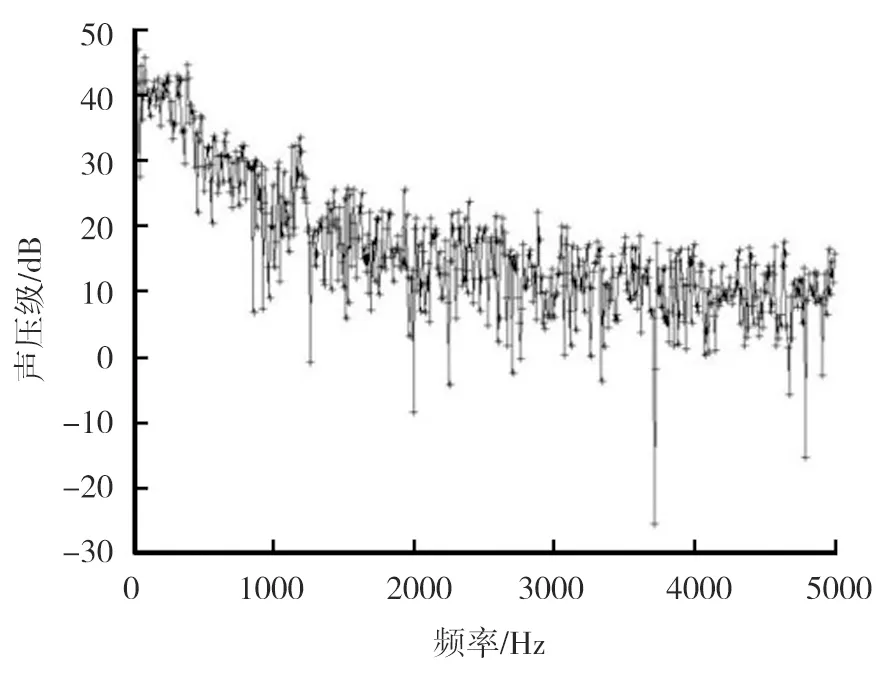
图9 350 km/h时频率-声压级分布
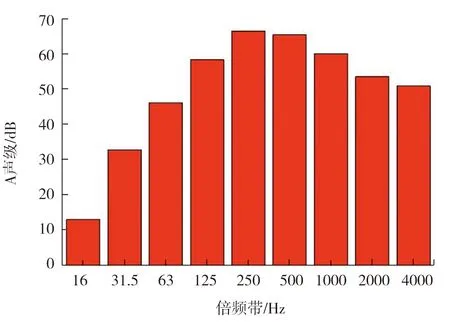
图10 350 km/h时倍频程的等效A声级分布
风速为400 km/h时的频率-声压级分布见图11。频率为0~5000 Hz时,声压级随频率的升高有下降的趋势,且趋势较陡,在低频范围内声压级较大,在高频范围内声压级很小。风速为400 km/h下的倍频程的等效A声级分布见图12。由图12可知风速为400 km/h时在250 Hz附近出现峰值,该频率成分的噪声对总噪声有较大贡献,说明该频率成分的噪声也是气动总噪声的主要组成部分,噪声能量主要集中在低频区。
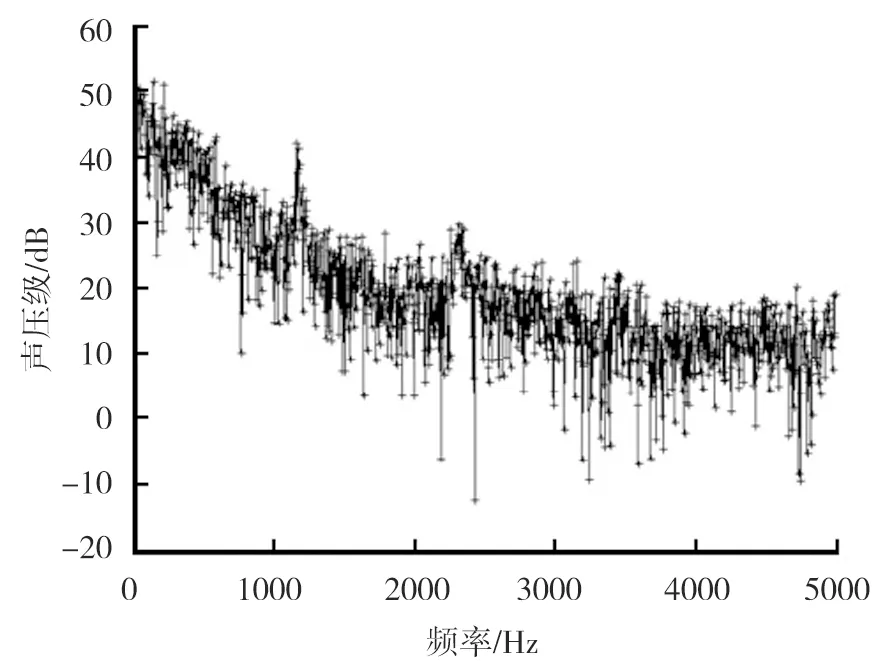
图11 400 km/h时频率-声压级分布
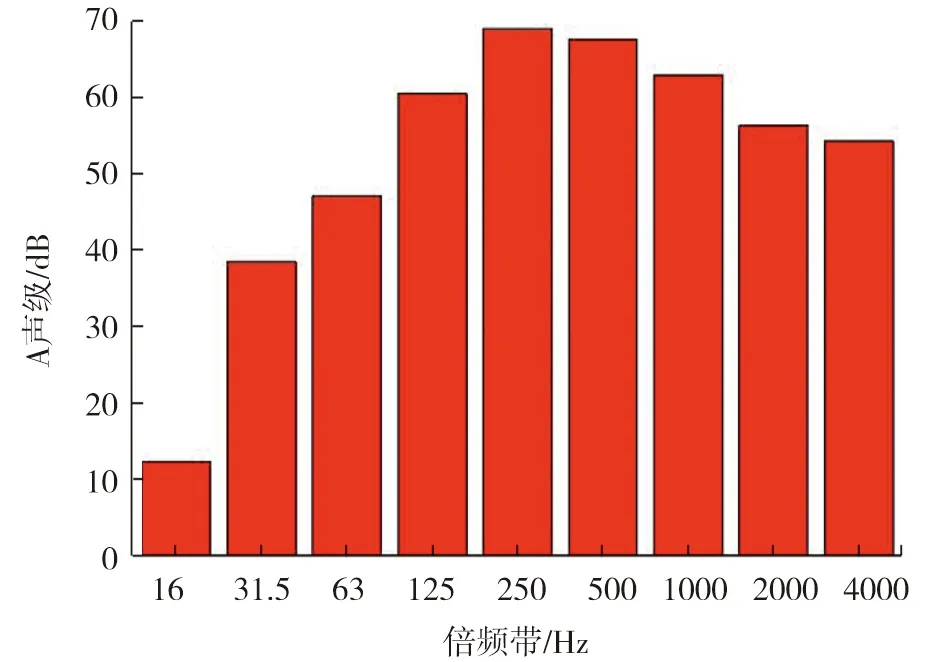
图12 400 km/h时倍频程的等效A声级分布
风速为500 km/h时的频率-声压级分布见图13。频率为0~2500 Hz时,声压级随频率的升高有下降的趋势,且趋势较缓,在低频范围内声压级较大,在高频范围内声压级很小。风速为500 km/h下的倍频程的等效A声级分布见图14。由图14可知,风速为500 km/h时在500 Hz附近出现峰值,该频率成分的噪声对总噪声有较大贡献,说明该频率成分的噪声也是气动总噪声的主要组成部分,噪声能量主要集中在低频区。
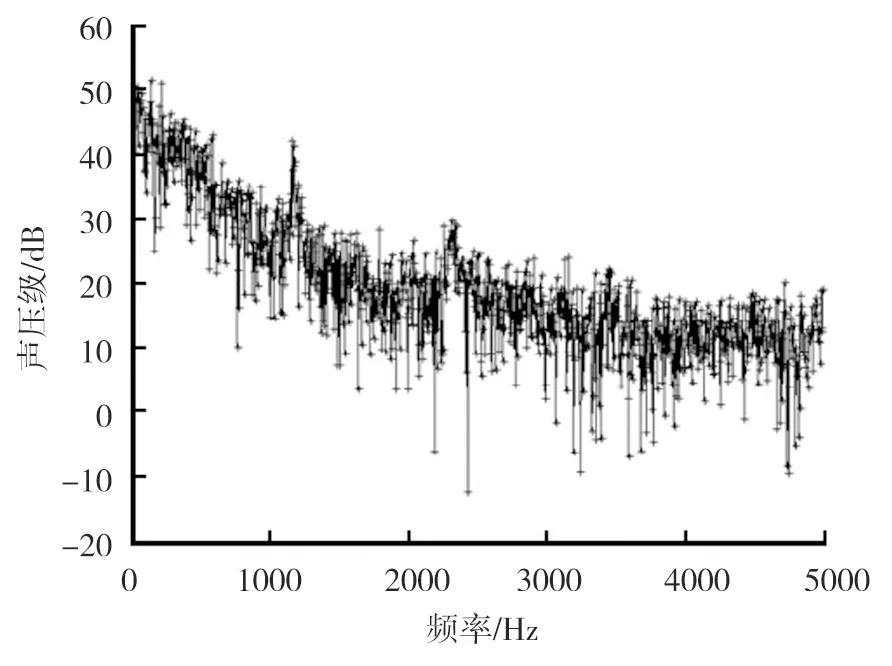
图13 500 km/h下频率-声压级分布
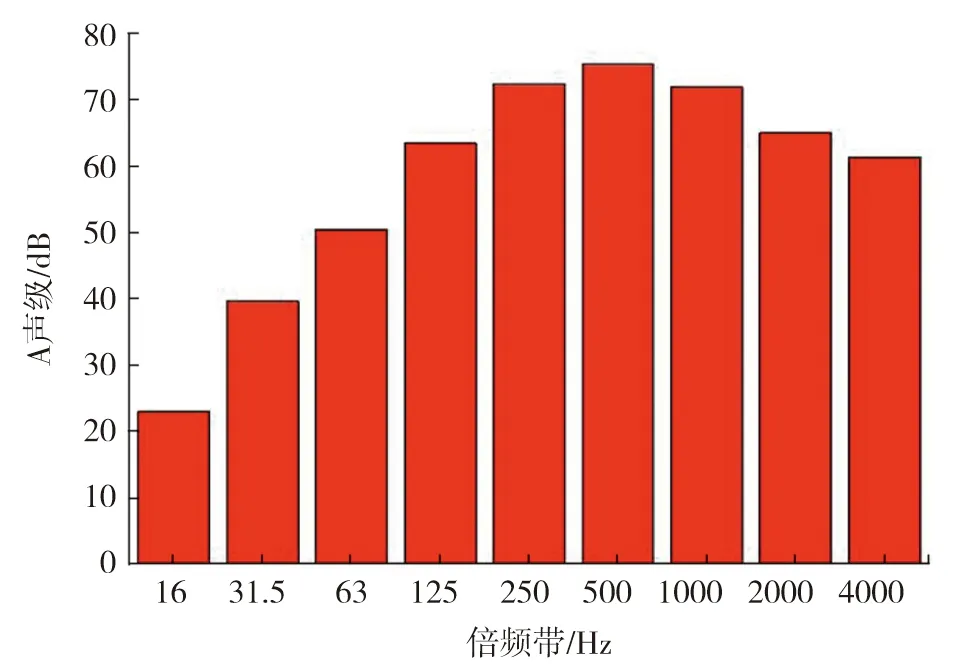
图14 500 km/h时倍频程的等效A声级分布
2.3 试验和计算比较
风速为36 km/h时的仿真和试验结果分别见图15、16,可以看出频率为0~2000 Hz时,声强级随频率的升高都有下降的趋势,仿真数据与试验数据基本吻合。
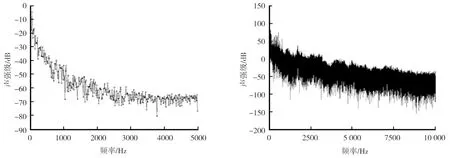
图15 36 km/h时的仿真结果 图16 36 km/h时的试验结果
3 结论
1)通过仿真与试验对比分析表明:频率为0~2000 Hz时,声压级随频率的升高有下降的趋势,在低频范围内声压级较大,在高频范围内声压级很小。建立的仿真分析模型基本能够反映声学风洞中微缩模型的试验情况,仿真分析数据与试验数据吻合度较高,噪声随频率的变化趋势基本一致,低速时气动噪声小,试验研究应进一步开发高速风洞。
2)从倍频程图中可以看出,4次不同风速的仿真均在100~500 Hz附近出现峰值,显然该频率成分的噪声对总噪声有比较大的贡献,说明该频率成分的噪声也是气动总噪声的主要组成部分,噪声能量主要集中在低频区。
3)为获得精确的声场计算结果,需要减少CFD采样时间步,增加采样时长,即增加CFD计算的瞬态数据量,以反映真实的声场变化情况。
4)高速列车的总气动噪声随车速的增大而升高。

