基于共振柱的海砂动剪切模量和阻尼比探究
(浙江海洋大学港航与交通运输工程学院, 浙江舟山316022)
0 引言
随着海洋工程的建设与发展,不同地域的海相砂土是否可以作为工程建设材料被使用,其中海相砂土的动剪切模量和阻尼比等动力特性是值得关注的重要参数。WICHTMANN等[1]针对石英砂开展了小应变动剪切模量和阻尼比的试验研究。其研究表明:除剪应变对其动力特性有较大影响外,塑性土含量也会影响其阻尼比。FERREIRA等[2]针对波尔图残积土的剪切模量开展了弯曲元和共振柱组合对比试验,同时也着重讨论了不同弯曲元的应用方法。GOUDARZY等[3]利用共振柱设备针对不同细粒含量的休斯敦砂开展不同围压下的动力参数测试,着重探究不同细粒含量与休斯敦砂的配比对动剪切模量和阻尼比的影响。国内学者对不同地域的海相土、沉积土也开展了不同条件下的共振柱试验。LING等[4]利用动三轴和共振柱设备对青藏铁路沿线的冻土开展一系列不同边界条件下的动力测试,研究成果表明温度和初始饱和度以及有效围压对永久性冻土的动剪切模量和阻尼比影响显著,阻尼比随着有效围压的增大而减小。
国内学者袁晓铭等[5]在哈尔滨地震力学研究所利用改良的共振柱仪设备针对国内多处地区的黏土、粉质黏土、砂土、淤泥质黏土等十多种土样在两种不同固结条件下开展大量的动力特性测试试验,得到一定动应变下试样的归一化动剪切模量和阻尼比,并且用最小二乘法对动剪切模量比、阻尼比和动剪应变之间的数量关系进行拟合,从而得到此类试样的动力学参数在某特定应变下的曲线推荐值。尹松等[6]利用共振柱开展了某海域海相沉积土的动力特性实验研究,提出了适用于海洋沉积土的一定应变范围内剪切模量比及阻尼比的推荐值。张亚军等[7]针对上海地区不同深度的软土展开动剪切模量和阻尼比的试验,并且对其动力参数进行了统计分析。吕程伟[8]利用GDS共振柱试验研究了纯黏土和水泥土—黏土复合试样的动剪切模量和阻尼比的变化规律。黄娟等[9]对昆明泥炭土的物理力学指标进行统计分析,得到其动剪切模量和阻尼比,并且修正了动剪切模量的拟合模型。战吉艳等[10]针对苏州海相沉积土开展一系列的动三轴和共振柱试验,统计了不同深度下的海相土动力特性。孙田等[11]以琼州海峡100m深度内的海相土为研究对象,探究深部海洋土动剪切模量和阻尼比的影响因素。王权民等[12]对厦门砂土进行动三轴和共振柱试验,获得了含泥中砂在小应变条件下阻尼比和动剪切模量的变化规律,给出了中粗砂与细粉砂的液化曲线和动本构关系,确定了相应的动孔压模型。陈国兴等[13-15]对苏南地区的海相,陆相沉积土开展了相关的试验研究,获得到大量关于苏南地区,尤其是南京周边不同深度土的动剪切模量和阻尼比等动力特性参数。
针对浙江沿海海相软土,汪明元等[16]利用动三轴设备研究了舟山岱山海相软土在循环荷载作用下动弹性模量和阻尼比变化规律,并获得了该海相软土的动应力、动应变、动孔压时程曲线和应力—应变关系曲线。王亚军等[17]研究了循环荷载作用下舟山海域海相砂土液化破坏孔压模型,并针对此土样修正了H-D模型。史法战等[18]利用GDS共振仪对舟山海域海底原状海相软土进行了一系列动力试验,研究了各深度范围土样在不同围压下动剪切模量和阻尼比随动剪切应变的变化趋势。这可以发现,围绕舟山海域软土动力特性的工作已有开展,而针对舟山海砂动力特性的研究尚少。然而,近年来舟山众多工程不断地通过吹沙填海造陆实现,因此,非常有必要深入理解和认识该海域海砂动剪切模量和阻尼比的特性。
基于Wille共振柱实验设备,本文将针对舟山某海域海砂开展其动剪切模量、阻尼比与动剪应变之间关系的研究,进一步分析理论模型和经验公式应用的合理性,以期望为未来的工程建设提供有价值的参考数据。
1 试验介绍
1.1 试验试样介绍及制备
本次试验的试样取自浙江省舟山市某海域的海砂,其颗粒级配曲线见图1,其物理性质见表1。

图1 海砂的颗粒级配曲线Fig.1 Particle grading curve of sea sand
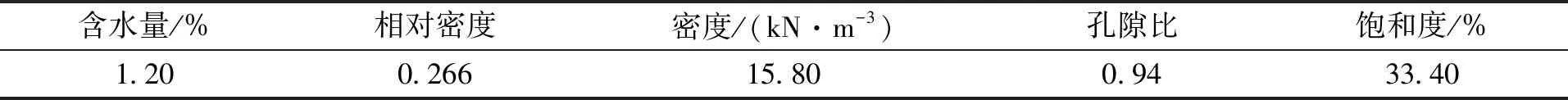
含水量/%相对密度密度/(kN·m-3)孔隙比饱和度/%1.200.26615.800.9433.40
根据所测的砂样颗粒级配曲线,可知该海砂的不均匀系数为Cu=d60/d10=2,曲率系数为Cc=(d302)/(d60×d10)=1.3,即该海砂级配不良;同时,可知该海砂粒径大于0.25 mm的颗粒含量大于整体砂样含量的50 %,即可判断为中砂[19]。
开始装样前,首先烘干砂样,确保砂样颗粒干燥,且颗粒均匀分布;然后分5层进行压实装样,每层压实遵循《土工试验方法标准》(GBT 50123—1999)[20],同时确保最后一层试样表面尽可能平整,以使试样和激振头完全接触,保证施加扭转振动时不偏心。试样的密实度为1.40 g/cm3。
1.2 设备以及试验步骤介绍
本次试验设备采用德国WillE公司生产的电磁共振柱。其中扭矩由电磁系统提供,可以在不损坏试样的条件下实现试样的动力特性测试,其测试加载应变可以达到10-7~10-4。具体的实验步骤为:①制样:抽真空装样,试样为圆柱形,尺寸是高度100 mm,直径50 mm;②设置边界条件:对试样逐级施加目标围压,然后通过负压吸水和加反压进水来调整实验所要求的饱和度,待试样的反压和孔压值稳定,即达到实验所需的饱和度;③激振:对稳定后的试样进行共振柱激振试验,整个过程都是通过微机控制,可以自动采集数据;④数据处理:当试验完成后,根据试验前测量的试验尺寸、密度,以及激振器在试样端部的作用方式,可以计算出各级围压,不同饱和度的动剪切模量G,其中还可以根据前后两次激振的振幅大小计算出阻尼比D。
值得注意的是:试验中不同围压下的试样激振结束后,都需要进行重新装样,而且要保证每次装样的密实度相同,本实验中每次装样的质量控制为272±2 g。
2 试验结果与分析
2.1 Gmax随围压σ和饱和度ω的变化规律
首先,试验中分析了围压的影响,即确保饱和度相同,分别对不同试样施加了200 kPa、300 kPa、400 kPa三种围压,变化规律如图2所示。
由图2可知,当试样的饱和度一定时,Gmax随围压增大而增大,其中围压为200 kPa时的Gmax最小,围压为400 kPa时的Gmax最大。随着围压增大,砂样被压实,其骨架结构愈来愈紧实,孔隙比减小,振动波在试样内部易于传播,传播速度变快。当试样处于同样的动应力状态中,剪应变越小,即Gmax越大。
其次,试验中也分析了饱和度的影响,即针对不同围压组饱和度分别为0,42 %,100 %的试样开展实验研究,其变化规律如图3所示。
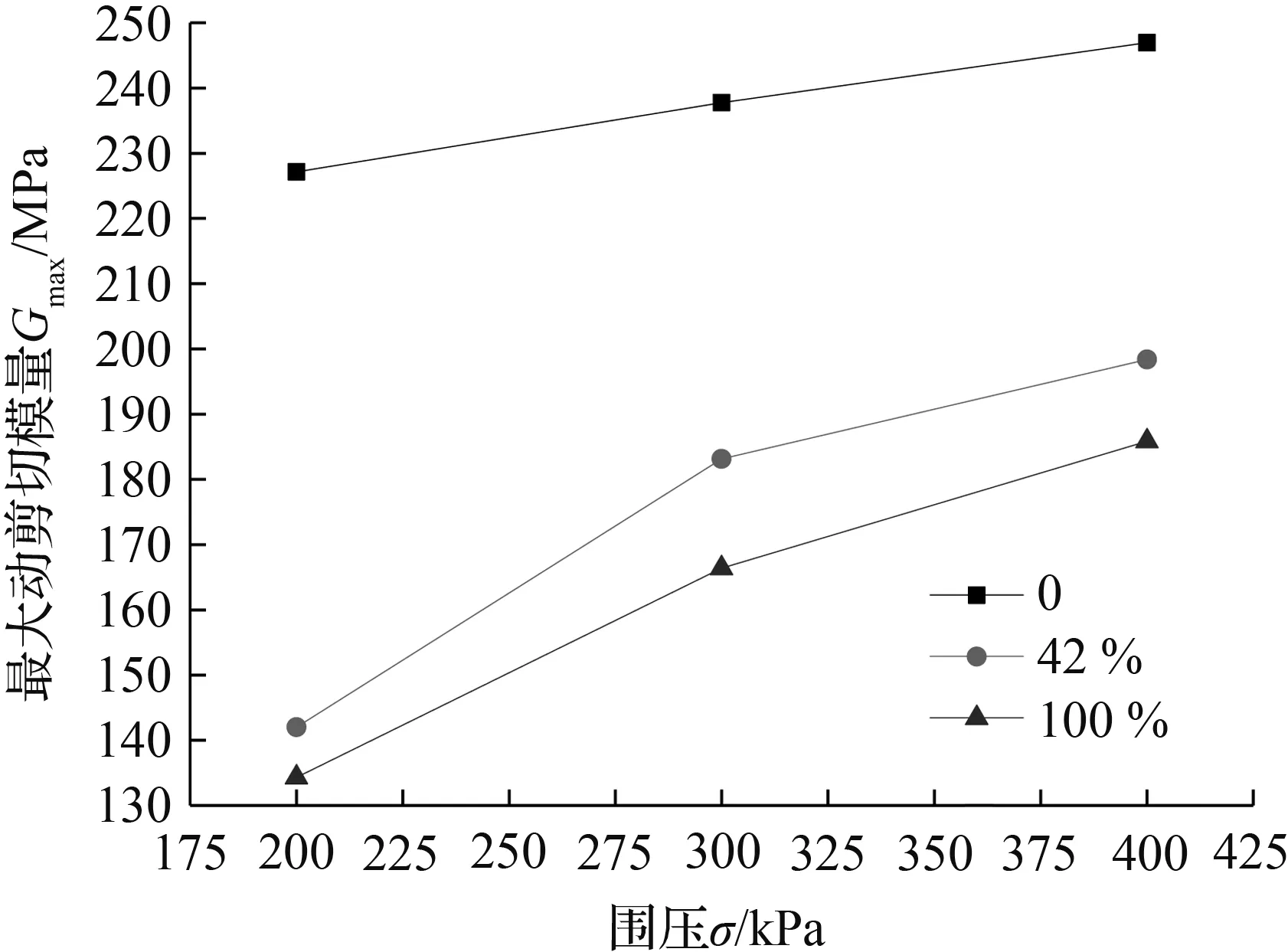
图2 饱和度分别为0、42 %、100 %时不同围压的海砂Gmax
Fig.2Gmaxof sea sand with different confining pressurewhen saturation is 0, 42 %, 100 %, respectively
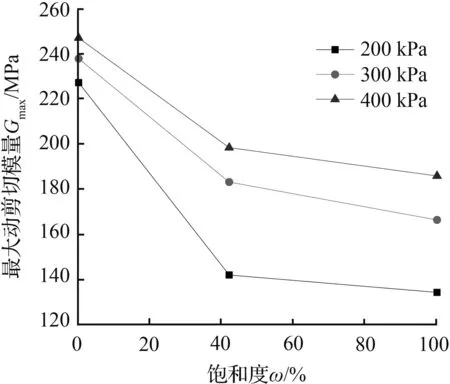
图3 围压分别为200 kPa、300 kPa、400 kPa时不同饱和度的海砂Gmax
Fig.3Gmaxof sea sand with different saturationwhen confining pressure is 200 kPa, 300 kPa, 400 kPa
由图3可知,当试样处于同一围压下,试样饱和度为0时Gmax最大,Gmax随饱和度增加不断减小。当试样处于较大围压下,Gmax受饱和度影响不是很明显。当对饱和度为0的试样施加围压时,试样颗粒间会产生良好的咬合效应,使试样的骨架结构紧实,整体刚度增大,即试样在干燥状态下的Gmax最大。当试样处于非饱和或饱和状态下,颗粒间含水使试样整体刚度减小,受到振动时更容易发生变形,则Gmax相较于干燥状态有所下降。
2.2 D随着剪应变γ及围压σ的变化规律
针对饱和度分别为0、42 %、100 %三种试样,本文也开展了海砂阻尼比随着剪应变变化规律的试验研究。
图4~图6分别为饱和度为0、42 %、100 %的海砂在围压200 kPa、300 kPa、400 kPa下阻尼比随剪应变的变化曲线。由上图4~图6可知,该海砂的阻尼比随动剪应变增大而增大,直到动剪应变达到3×10-5时,曲线均呈现明显的收敛趋势。这可能主要是由于当动剪应变逐渐增大直到后期,砂样自身的动剪应变也累积到一定程度,最初的砂样内部结构已经被调整,砂样内部颗粒间的接触点越来越多,振动波穿过砂样时消耗的能量较为平稳[14]。此外,由图4~图6可知,在小应变作用下,围压对砂样阻尼比的影响较为明显,在动剪应变一定的情况下,围压越小,阻尼比越大。这可能是由于当砂样处于低围压应力状态时,砂样整体的骨架结构较为疏松且内部存在孔隙水,导致振动波要耗费较多的能量来穿过砂样,所以造成围压小而阻尼比大的现象。当围压增加时,试样整体受到压缩,骨架结构较为紧实,砂样颗粒间的孔隙也变小,使得振动波易于穿过砂样,砂样整体对于振动波的能量消耗相对较少,即造成一定应变下高围压而阻尼比小的现象。

图4 干砂的阻尼比随剪应变的变化
Fig.4 Variation of damping ratio ofdry sand with shear strain

图5 饱和度为42 %的海砂的阻尼比随剪应变的变化
Fig.5 Variation of damping ratio of sea sandwith shear strain as its saturation is 42 %

图6 饱和度为100 %的海砂阻尼比随剪应变的变化Fig.6 Variation of damping ratio of sea sand with shear strain as its saturation is 100 %
2.3 海砂G/Gmax-γ和D-G/Gmax的拟合曲线及拟合方程参数值
为了更详细地分析该海砂的动力特性,本文也给出小应变下动剪切模量比和阻尼比的推荐值,此时选择合适的预测模型是非常关键的。
本文拟选用三参数的Martin-Davidenkov模型[3]对该海砂的动剪切模量比曲线数据进行拟合分析,其模型如下:
G(γ)=Gmax(1-f(γ)),
(1)
(2)
其中:A、B是与砂样有关的拟合参数,根据相关试验数据具体确定。
对于阻尼比与动剪应变关系的拟合,本文拟选用经验公式[3]:
D=Dmin+D0(1-G/Gmax)n,
(3)
其中,D0是反映土固有属性的小应变阻尼比,Dmin是最小阻尼比,n是与砂样性质有关的拟合参数,根据相关实验数据可以确定。
如图7所示,给出不同围压、不同饱和度砂样的G/Gmax-γ数据在M-D模型下的拟合曲线,由图7可知,砂样的动剪切模量比随动剪应变的增大而减小。除去图7(a)的前半部分数据的拟合效果略微有些离散,M-D模型可以较好地拟合G/Gmax-γ实验数据。
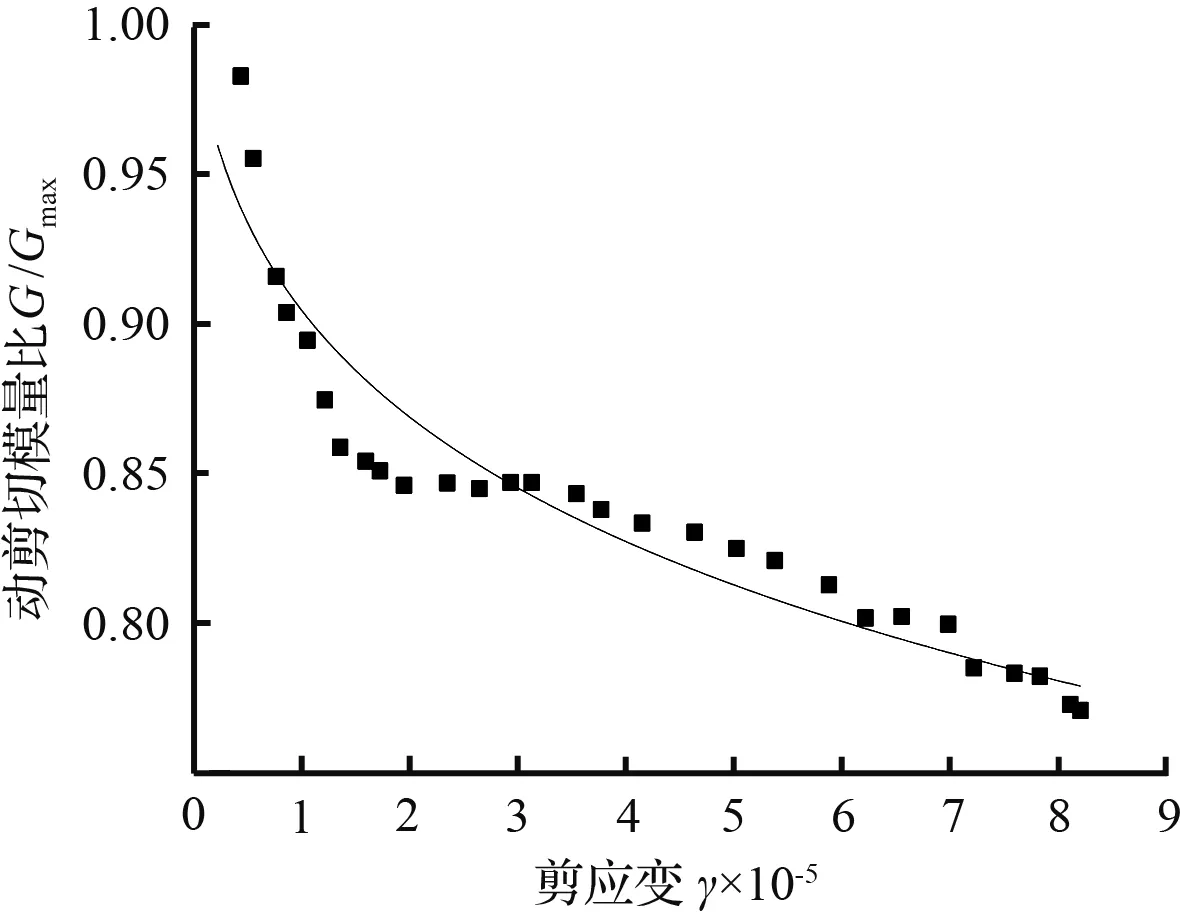
(a) σ为200 kPa,ω为0 %试验点
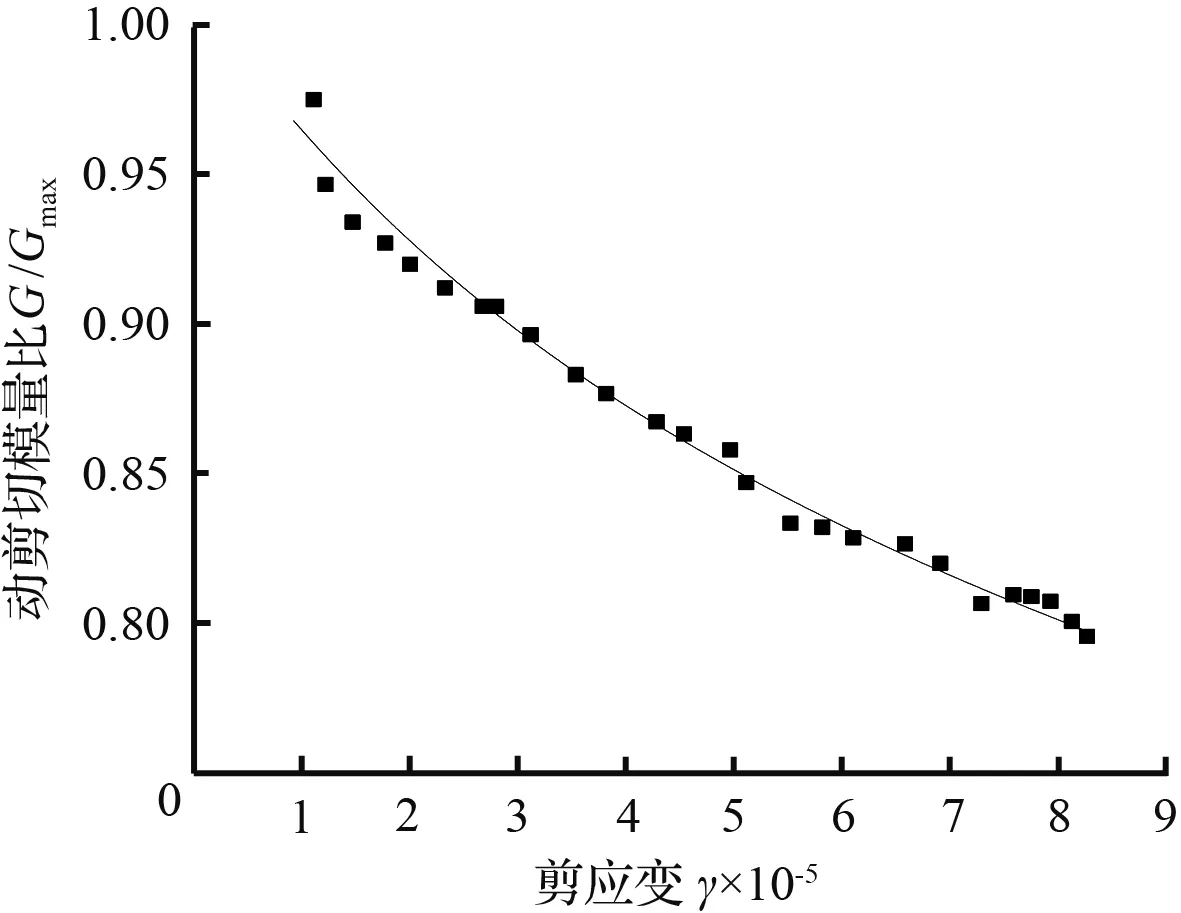
(b) σ为300 kPa,ω为0 %试验点

c) σ为400 kPa,ω为0 %试验点
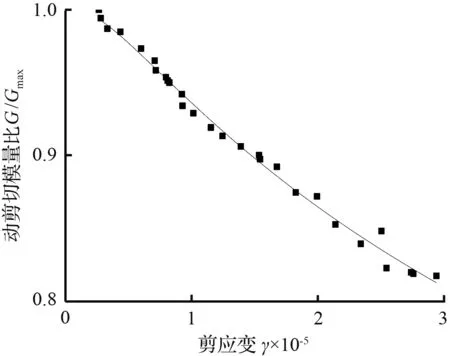
(d) σ为200 kPa,ω为42 %试验点

(e) σ为300 kPa,ω为42 %试验点
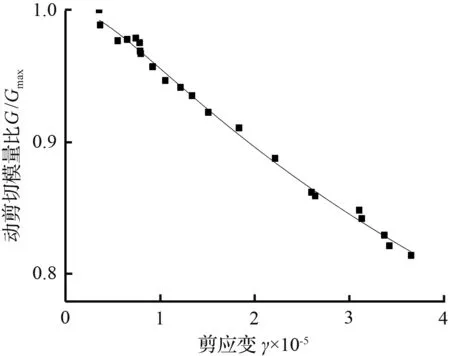
(f) σ为400 kPa,ω为42 %试验点
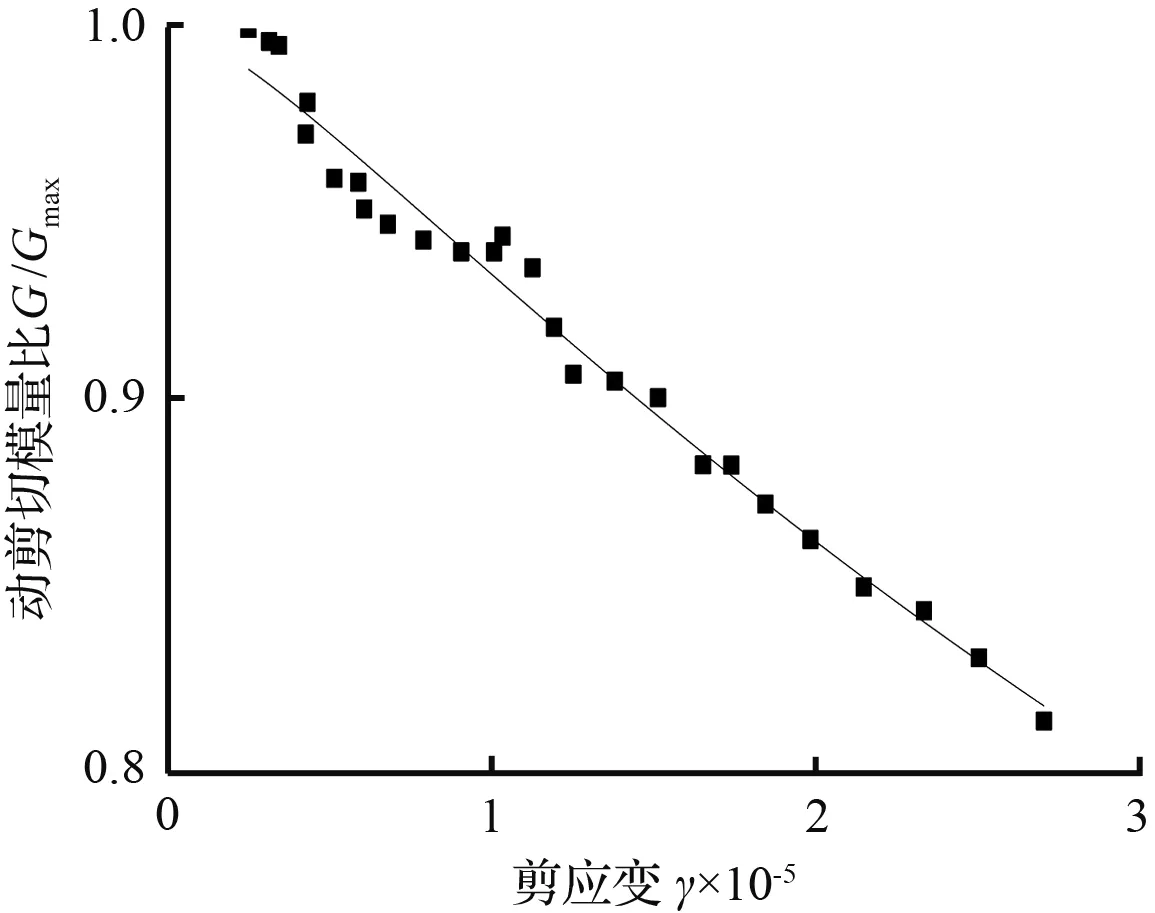
(g) σ为200 kPa,ω为100 %试验点

(h) σ为300 kPa,ω为100 %试验点
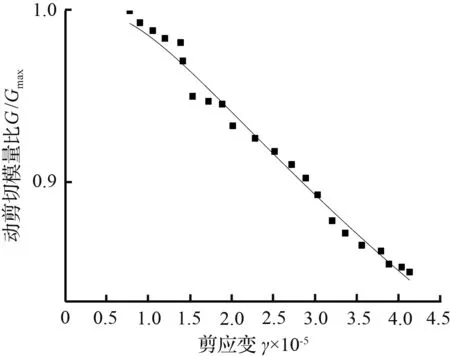
(i) σ为400 kPa,ω为100 %试验点
如图8所示,给出不同围压、不同饱和度砂样D-G/Gmax数据在阻尼比经验公式下的拟合曲线,由图8可知,砂样的阻尼比与动剪切模量比呈现负相关变化趋势,而动剪切模量比与动剪应变也呈现负相关变化趋势,所示试样的阻尼比随动剪应变呈现正相关变化趋势,这与上部结论相呼应。除去图8(g)~图8(h)的部分数据的拟合效果略微有些离散,阻尼比经验公式可以较好地拟合D-G/Gmax实验数据。
进一步,为了更好地为海岛工程建设提供合理的海砂动力学参考值,根据M-D模型和阻尼比经验公式对实验进行拟合,本文给出了对应于不同围压和饱和度条件下,该海砂在小应变下M-D模型和阻尼比经验公式拟合方程的参数(见表2),据此可以直接获得某特定应变下的动力参数。
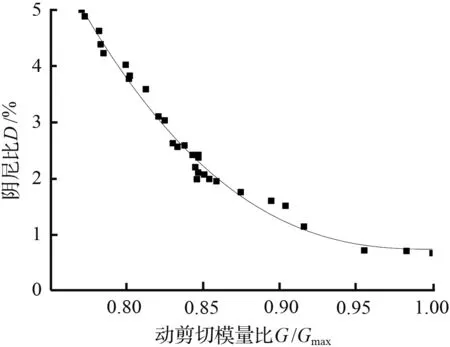
(a) σ为200 kPa,ω为0 %试验点
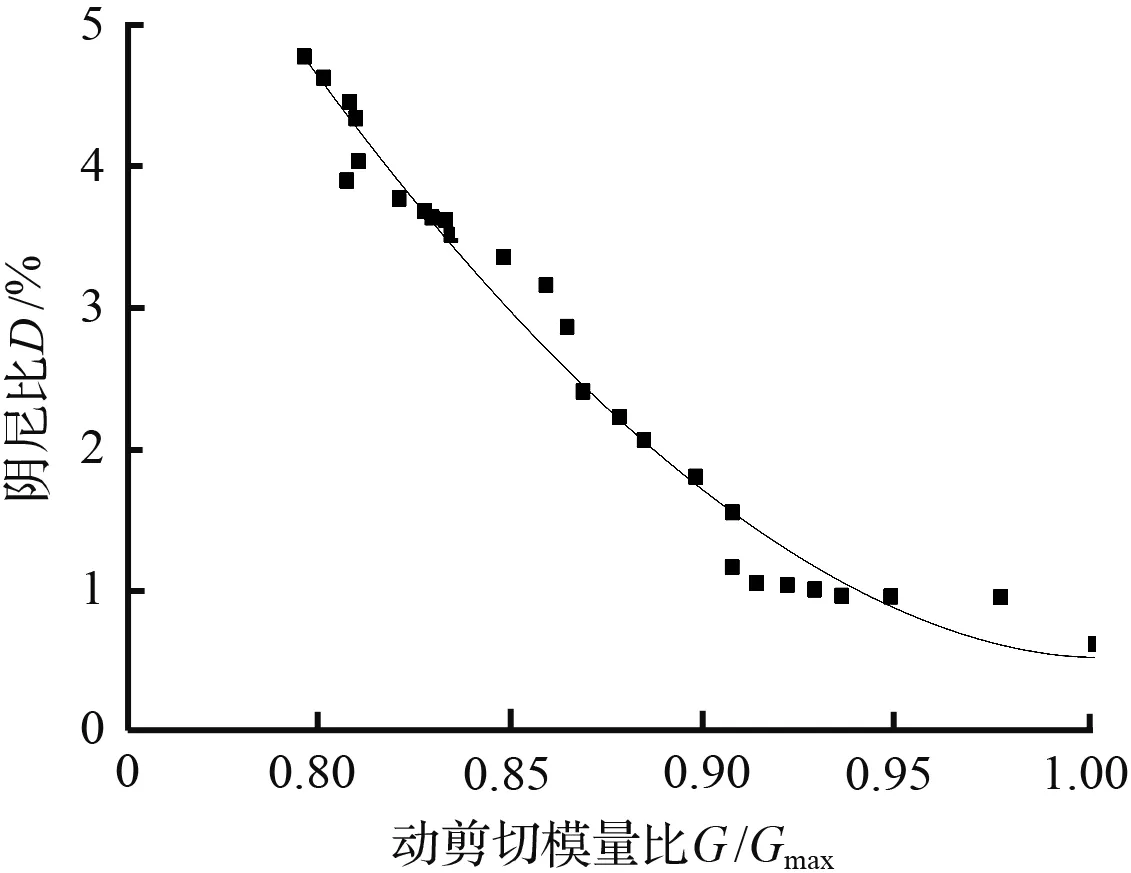
(b) σ为300 kPa,ω为0 %试验点
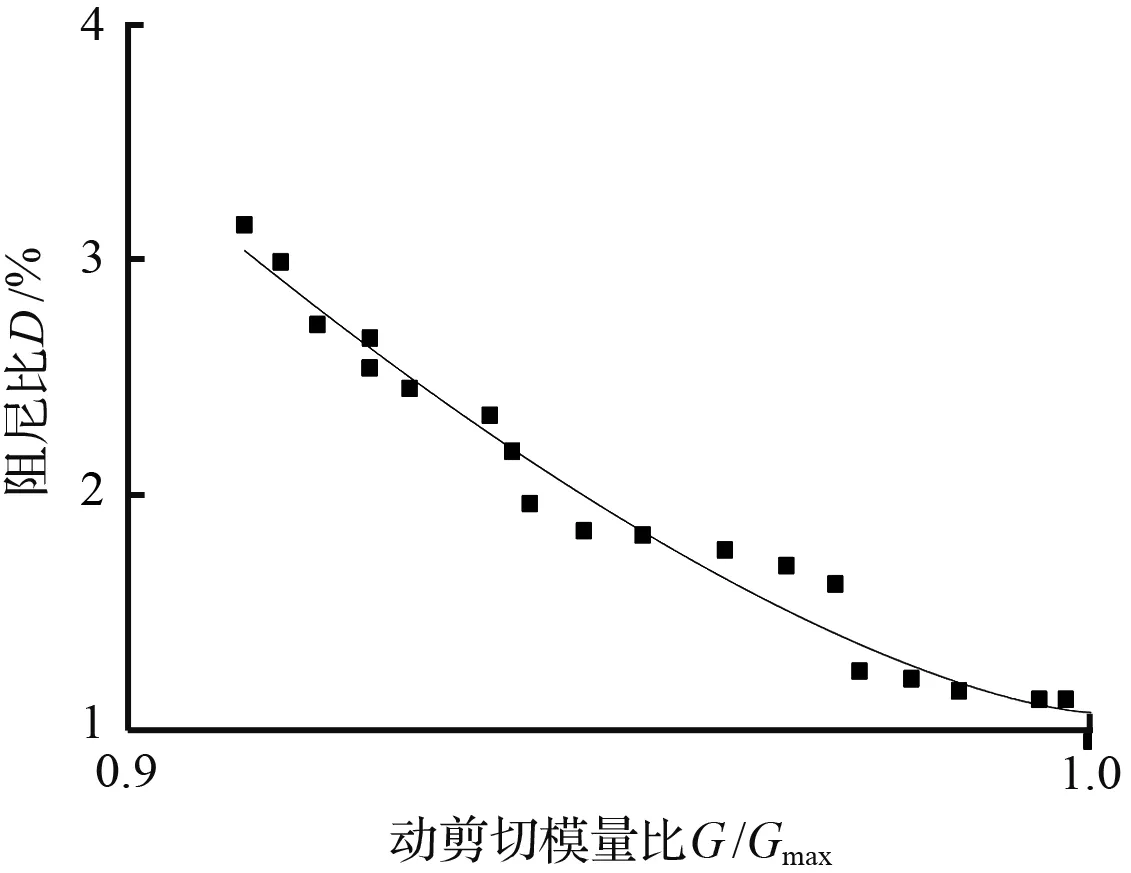
(c) σ为400 kPa,ω为0 %试验点
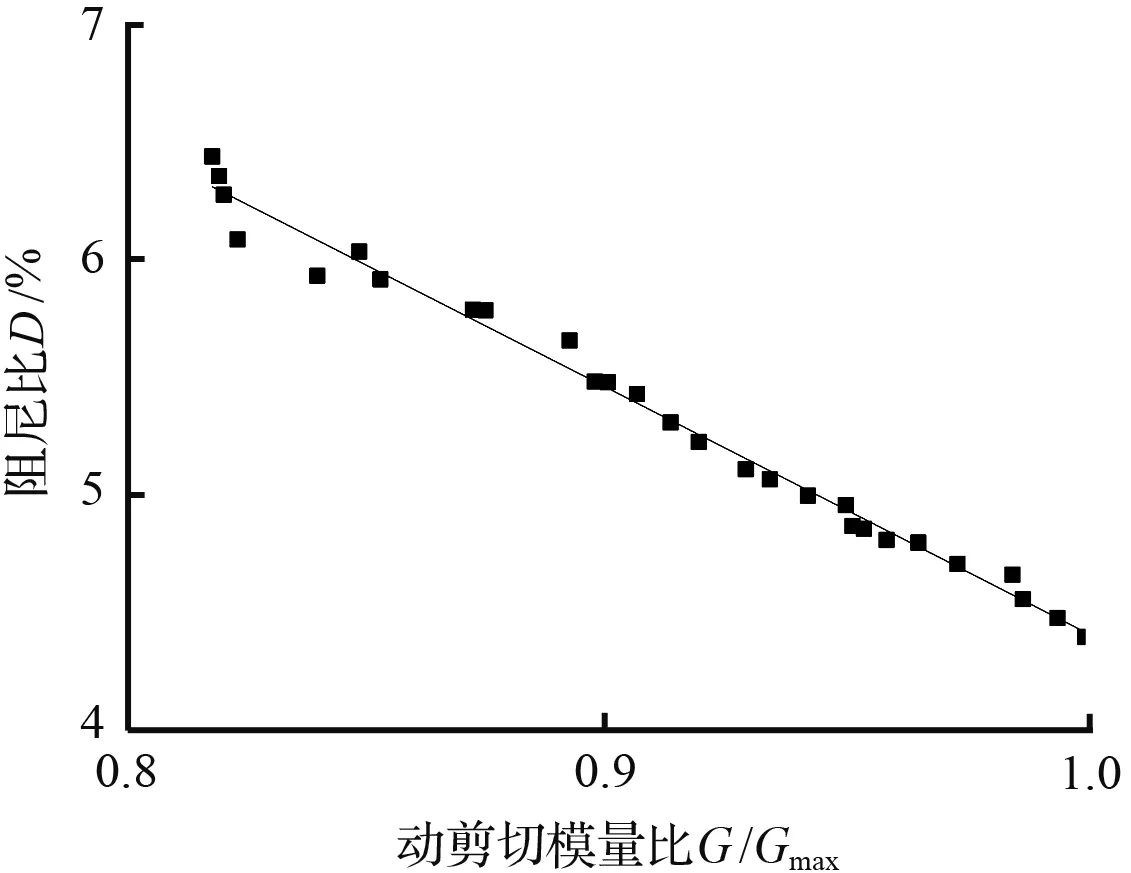
(d) σ为200 kPa,ω为42 %试验点

(e) σ为300 kPa,ω为42 %试验点
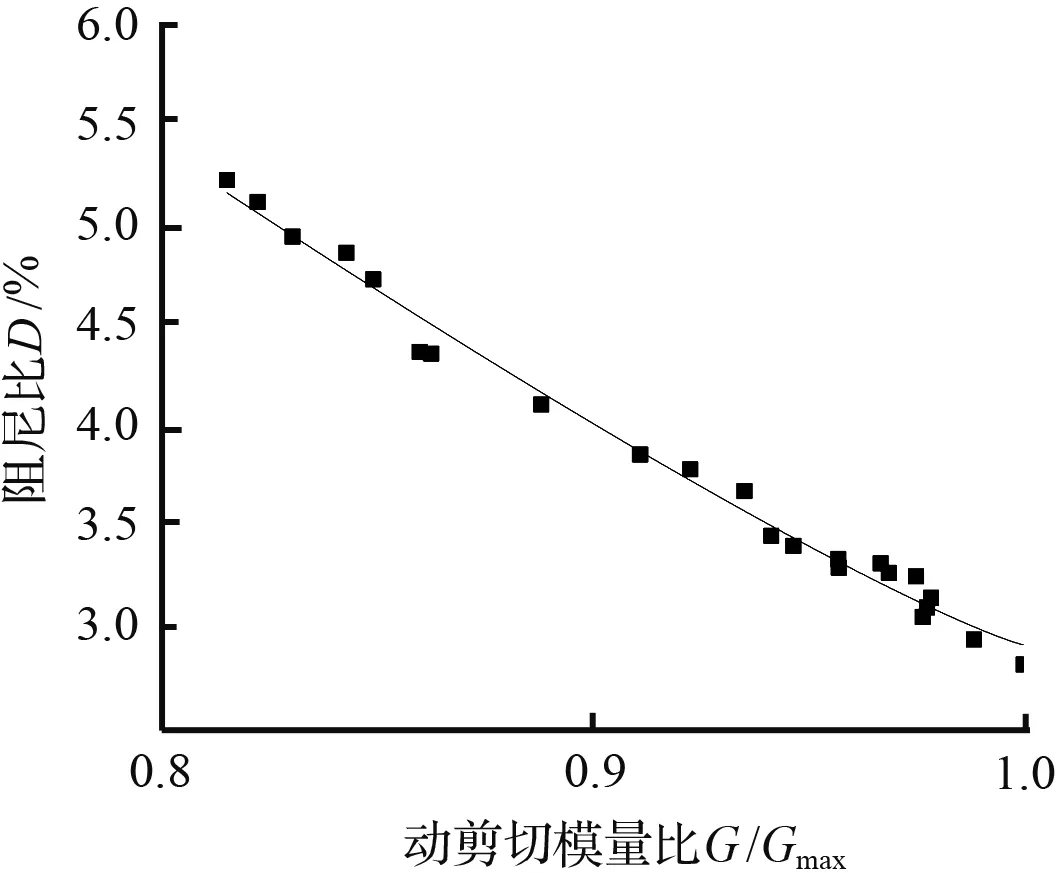
(f) σ为400 kPa,ω为42 %试验点
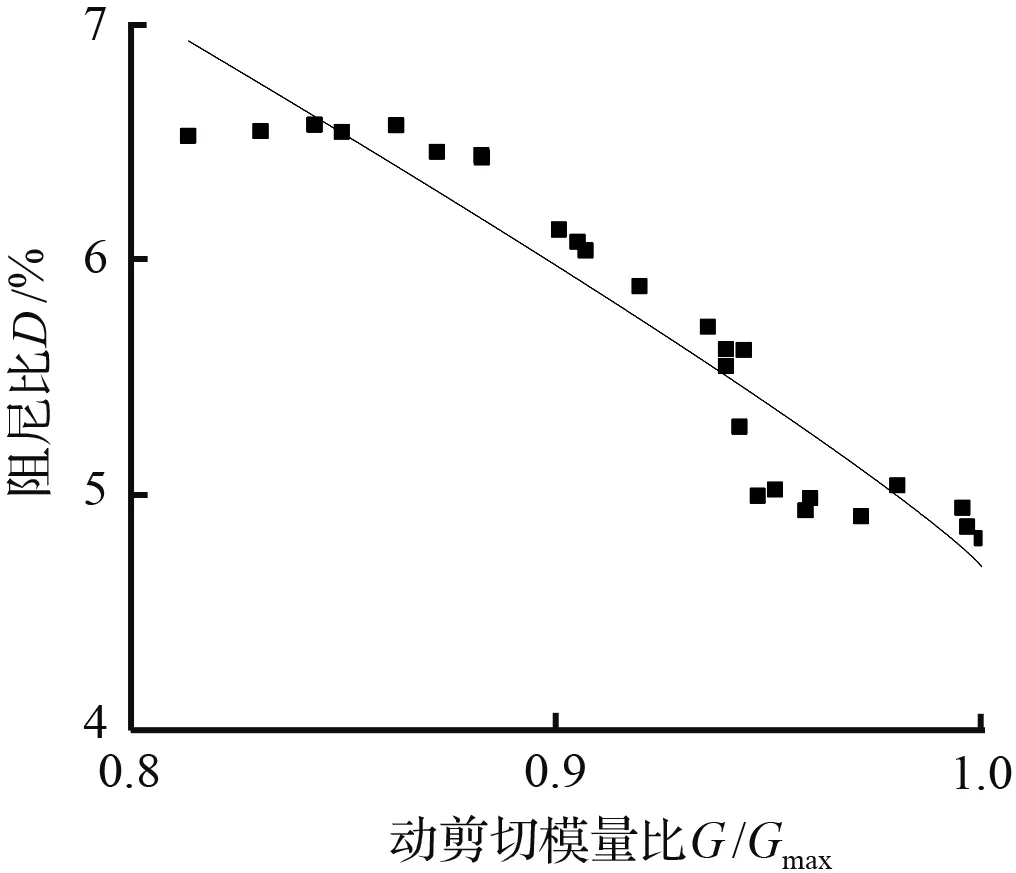
(g) σ为200 kPa,ω为100 %试验点
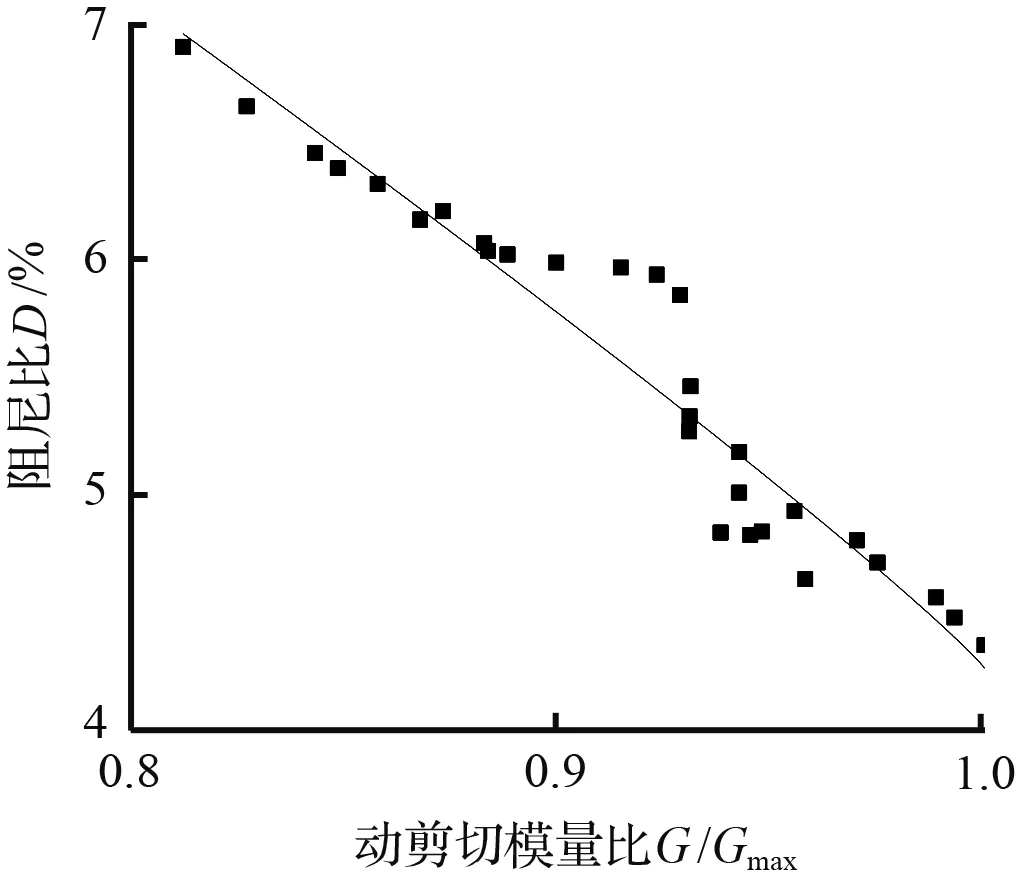
(h) σ为300 kPa,ω为100 %试验点
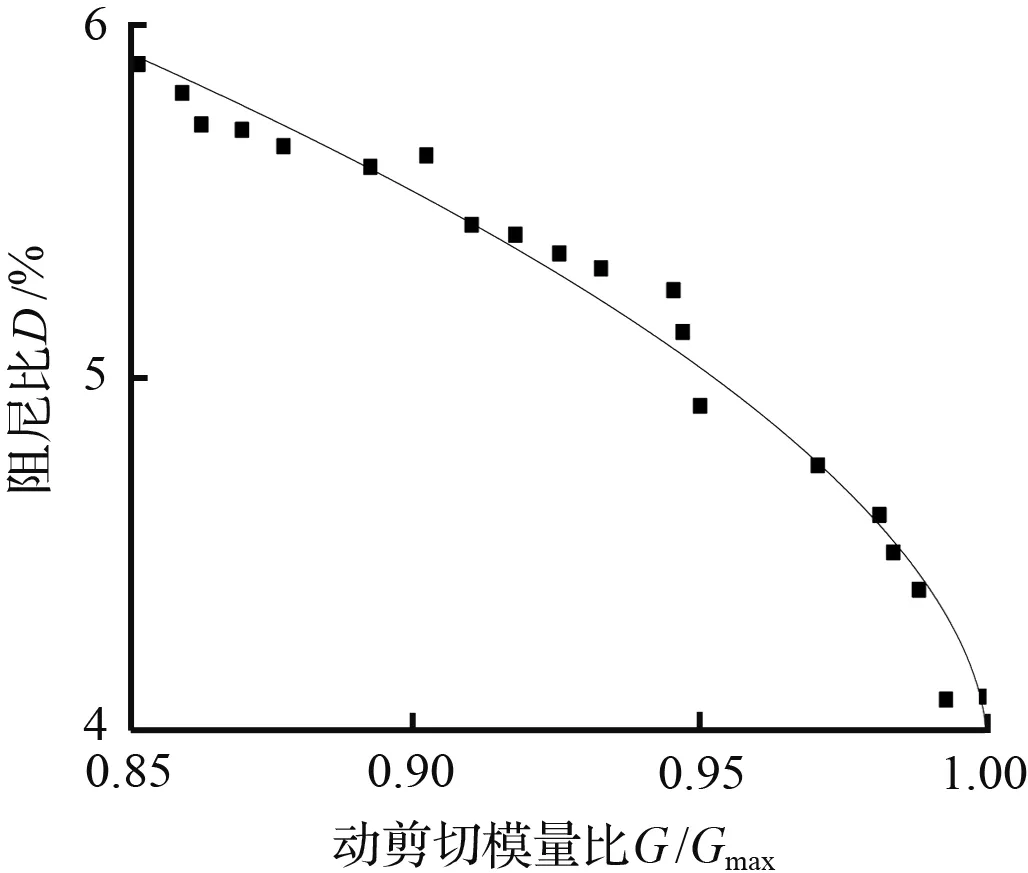
(i) σ为400 kPa,ω为100 %试验点

饱和度/%围压/kPa拟合参数A拟合参数B参考剪应变γ0最小阻尼比Dmin小应变下阻尼比D0拟合参数n0200 2.213 90.369 33.29×10-50.007 41.711 12.502 303000.152 93.198 71.96×10-40.005 30.766 11.820 10400295.797 00.293 97.39×10-90.010 60.721 21.477 542200112.542 00.232 33.50×10-90.044 20.103 40.997 342300144.783 00.264 67.61×10-90.030 20.085 40.660 94240010.934 30.262 71.39×10-60.029 30.157 21.160 310020071.814 90.106 71.19×10-120.046 80.101 70.894 410030087.048 10.177 91.13×10-120.038 10.146 70.920 6100400166.668 00.214 14.31×10-90.039 80.056 00.559 4
3 结论
①舟山海砂在干燥、非饱和、饱和状态下Gmax随围压σ增大而增大,其中当σ一定时,干燥状态的Gmax值最大。当动剪应变γ一定时,D随σ增大而减小。当σ一定时,D随γ的增大而增大。
②舟山海砂G/Gmax随γ的增大而减小,D随γ的增大而增大,其中当γ累积到后期时,对阻尼比的影响不是很明显,阻尼比D值开始呈现收敛趋势。
③Martin-Davidenkov模型以及D-G/Gmax的经验公式可以很好地拟合G/Gmax和D与G/Gmax的变化规律,据此提出的舟山海砂关于G/Gmax和D的拟合方程参数值,可以为未来海岛工程勘测与设计提供参考依据。

