弹性阶段波形钢腹板组合梁体外预应力增量

(山东大学岩土与结构工程研究中心， 山东济南250061)

0 引言

波形钢腹板组合梁是指用波折形钢板代替混凝土腹板，顶板和底板仍旧采用钢筋混凝土结构的一种钢混组合桥梁结构，这种组合结构拥有了钢和混凝土的力学优点，在国内外应用广泛。目前，波形钢腹板组合梁的研究重点是抗弯、抗剪、内衬混凝土部位抗剪和抗扭等方面[1-7]，然而，关于波形钢腹板组合梁体外预应力筋应力增量的研究还较少。

波形钢腹板组合梁一般采用体内束和体外束混合配束的形式，所以体外预应力筋应力增量对梁体挠度的影响不容忽视。实际桥梁工程中更关注的是正常使用阶段下体外预应力筋应力增量的变化规律，所以开展弹性阶段波形钢腹板组合梁体外预应力筋应力增量的研究具有深刻的理论意义和实用价值。弹性阶段体外预应力筋应力增量的影响因素有很多，理论公式较为复杂也并没有统一的算法，因此，国内外研究学者在体外预应力筋应力增量方面开展了相关研究。

2004年同济大学徐栋等[8-9]学者基于研发的体外预应力PC梁的弹性阶段非线性分析程序，研究了中小跨径桥梁跨高比、体外预应力钢束与结构的粘结关系以及转向块间距等参数对体外预应力钢束活载作用下的应力变化的影响规律，但这些规律并不适用于大跨径PC梁桥。2006年张峰[10]等学者研究了“二次效应”对体外预应力混凝土梁桥的影响规律，得出桥梁在正常使用阶段的设计中可以不考虑“二次效应”的结论。2008年刘钊等[11-12]学者基于能量法和挠度的统一算法推导了弹性阶段简支梁体外预应力筋应力增量的解析解公式，但是这并不是针对波形钢腹板组合梁的计算公式。河海大学袁爱民等[13]学者开展了节段预制箱梁体外束极限应力增量计算方法的研究。2017年浙江大学徐荣桥等[14]学者构造了适用于考虑滑移的体外预应力筋的有限单元，将其应用到体外预应力筋的分析理论。

综上所述，已有的体外预应力筋应力增量的研究成果多是集中在预应力PC梁桥，对于波形钢腹板组合梁体外预应力筋应力增量的研究还不充分，应力增量的影响因素还不明确。本研究基于波形钢腹板组合梁抗弯承载力模型试验，结合理论分析和参数拟合分析，推导了弹性阶段体外预应力筋应力增量的计算公式，研究了应力增量的影响因素。

1 模型试验

模型试验梁的跨径为4.4 m，共设计4个横隔板，预应力钢筋设置2根Φ15.24钢绞线。具体截面尺寸、体外预应力筋及普通钢筋布置参见图1。

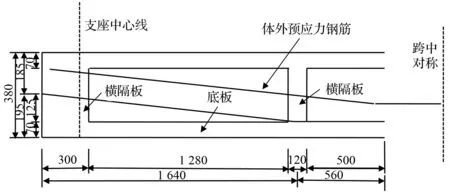
(a) 立面图

(b) 横截面

图1 模型横截面尺寸
Fig.1 Model cross-sectional dimensions

根据相关技术规范规程，参考拌合站集中拌制C50混凝土的设计配合比，制作了9个150 mm×150 mm×150 mm的混凝土立方体标准试块，并进行了混凝土立方体强度测试(见表1)。

表1 混凝土立方体抗压强度Tab.1 Cube compressive strength of concrete block

波形钢腹板采用4 mm厚的钢板，细部尺寸参见图2。普通钢筋采用8 mm的Q235热轧光圆钢筋，钢筋抗拉强度为210 MPa，d表示直板段宽度，f表示斜板段投影宽度，e表示斜板段宽度。

图2 波形钢腹板尺寸LFig.2 Size of corrugated steel web L

试验梁利用反力架做支撑，采用千斤顶进行分级加载，加载方式为两点对称加载(图3)。为研究锚下有效预应力沿体外预应力筋的纵向分布，模型试验采用3F108穿心式压力传感器和JMZX系列综合测试仪测试锚下有效预应力。在试验梁的2根钢绞线的张拉端和锚固端均放置压力传感器，共计4个压力环，具体测试照片参见图4。

图3 试验加载图
Fig.3 Test loading

4 锚下预应力测试
Fig.4 Anchor prestressed test

图5 锚下有效预应力变化Fig.5 The result of anchor prestressed test

模型梁体外预应力筋张拉端、固定端在不同荷载作用下的锚下有效预应力测试结果如图5所示，图5中1-1表示体外预应力钢绞线1固定端；1-2表示体外预应力钢绞线1张拉端；1-3表示体外预应力钢绞线2固定端；1-4表示体外预应力钢绞线2张拉端。

分析图5可以看出：模型梁在加载过程中，锚下有效预应力沿钢绞线纵向分布规律大致相同。在弹性阶段；各个测点锚下有效预应力分别为3.2 kN、3.4 kN、3.3 kN和3.3 kN，取4个传感器测试结果的平均值作为锚下有效预应力的测试结果，故可认为模型梁在弹性阶段的应力增量为25.9 MPa。

2 理论分析

2.1 弹性阶段体外预应力筋应力增量计算方法

根据梁体挠曲变形前后的几何关系，由材料力学方法可给出梁体产生挠曲变形w(x)后，dx梁段内无粘结力筋的伸长量为：

d(ΔL)=-e(x)w″(x)dx，

(1)

式中：ΔL为力筋总伸长量；e(x)为力筋偏心距；w(x)为梁体挠曲变形曲线。

体外预应力筋应力增量计算的基本方程为：

(2)

式中：e(x)为体外预应力筋偏心距；w(x)为组合梁的挠曲线方程；Eps为预应力筋的弹性模量。

通过分析图6可以看出，体外预应力筋和梁体在外荷载作用下变形不协调，导致体外预应力筋的偏心距会随着梁体的变形发生变化，产生“二次效应”现象，所以在推导三折线布筋梁体变形后力筋的偏心距e(x)时，需要对比分析“二次效应”的影响，图6中w(λL)和w(L-λL)为梁体转向块处挠度。

考虑“二次效应”：

(3)

不考虑“二次效应”：

(4)

式中：em、es为预应力筋水平端和锚固端至截面形心的距离；w(x)为梁体挠度；w(λL)和w(L-λL)为梁体转向块处挠度。

分析式(2)～(4)可以看出：弹性阶段波形钢腹板组合梁体外预应力筋应力增量的解析解推导需要首先确定梁体挠度。后续章节将针对波形钢腹板组合梁进行挠度的解析解推导。

2.2 两点对称加载跨中挠度计算

“顶、底板抗弯，腹板抗剪”是波形钢腹板组合梁设计基本原则，本研究将按照上述原则开展公式推导，即考虑两种挠度的叠加：①顶板和底板产生的弯曲变形；②腹板的剪切变形。

同时考虑到两点对称加载的挠度解析解推导可基于集中荷载作用下的挠度解析解进行叠加计算，以下给出集中荷载作用下的挠度解析解推导过程。

集中力F作用下简支梁(图7)的剪力和弯矩表达式：

(5)

(6)

式中：a、b为图7中集中力F距梁两端距离；F为外荷载；L为简支梁跨径。

波形钢腹板组合梁的剪切模量采用效剪切模量Ge[15]，因此截面的剪切刚度计算公式如下：

Ge=G(d+f)/(d+e)，

(7)

式中：G为钢的剪切模量；Ge为钢腹板等效剪切模量；d、f、e的具体尺寸见图2。

设剪力单独作用时，梁挠度曲线上任意点斜率等于该处截面的剪应变，可得到：

(8)

式中：w1为梁在剪应力作用下的挠度；As为左右钢腹腹板面积之和；Q(x)为剪力。

波形钢腹板简支梁剪切变形挠度w1：

(9)

波形钢腹板简支梁弯矩导致的挠曲线w2和截面弯矩的关系为：

(10)

式中：w2为集中荷载F作用下的挠度；Ec为混凝土板弹性模量；Ic为上、下混凝土板对混凝土板形心轴的惯性矩，波形钢腹板纵向刚度很低，不计波形钢腹板的弯曲刚度；M(x)为弯矩。

将式(6)代入式(10)，解得：

(11)

根据叠加原理，可得如图8所示的模型梁挠度计算公式：

(12)

图7 集中力F作用下简支梁计算简图
Fig.7 Calculation diagram of simply supportedbeam concentrated forceF

图8 两点对称加载下简支梁计算简图
Fig.8 Calculation diagram of simply supportedbeam under under two-point symmetric loading

2.3 体外预应力束增量推导

将式(12)、式(3)和式(4)代入式(2)，得到考虑和不考虑“二次效应”的弹性阶段Δσps的计算公式：

考虑“二次效应”：

(13)

不考虑“二次效应”：

(14)

通过上述基于变形的体外预应力筋应力增量解析解的推导过程和应力增量影响因素的分析可知，在弹性范围内波形钢腹板组合梁体外预应力筋应力增量的影响因素有：加载位置到梁端支座的距离、预应力筋布置形式、混凝土弹性模量、转向块数量和布设、梁高和波形钢腹板厚度与梁高的比值等等。

3 解析解公式验证

对比分析模型试验的测试结果和解析解计算结果，同时选取参考文献[2]和文献[16]的试验测试结果进行对比分析(表2)。

表2 计算值和试验值对比分析Tab.2 Comparative analysis of theoretical calculation and test

分析表2可得：

①本研究推导的理论公式对两点对称加载的模型梁的计算结果均比试验结果要小，但都在计算允许范围内；

②在弹性阶段“二次效应”对体外预应力增量的影响为0.2 %，可以忽略。

4 参数分析

进一步对弹性阶段体外预应力筋应力增量建议计算公式开展参数拟合分析，重点研究混凝土弹性模型、加载点到梁端支座距离、梁高和波形钢腹板厚度与梁高比值等参数对应力增量的影响规律，具体分析结果如图9～图12所示。

图9 混凝土弹性模量的影响
Fig.9 Effect of elastic modulus of concrete

图10 加载点到梁端支座距离的影响
Fig.10 Effect of the distance fromloading postion to the beam end

分析图9可以看出：随着混凝土弹性模量的增大，预应力筋应力增量呈现递减趋势，且递减曲线是线性递减。分析其原因是：随着弹性模量的增大，波形钢腹板箱梁的抗弯刚度增大，所以在相同荷载下，梁体变形减小，体外预应力筋的应力增量减小。

分析图10可以看出：当加载点到梁端支座距离为1/3梁的纵向长度时，体外预应力增量最小，当加载点距离梁端支座的距离越小时，体外预应力增量最大。

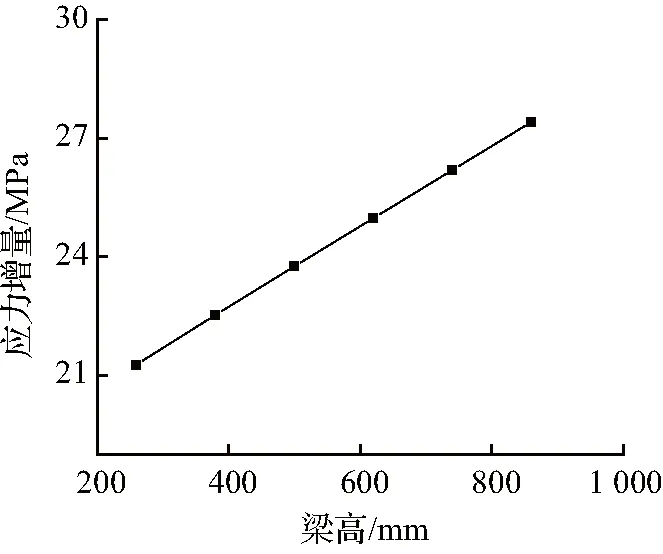
图11 梁高的影响
Fig.11 Influence of high of beam

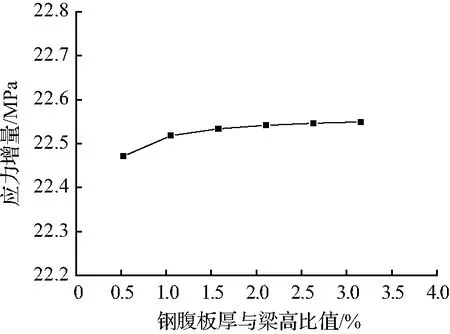
图12 钢腹板厚度与梁高比值的影响
Fig.12 Influence of ratio of steel webthickness to beam high postion

分析图11可以看出：在弹性阶段，梁高和预应力筋应力增量呈现线性增加规律。分析其原因是：随着梁高的增大，预应力筋距离截面形心轴的距离增大，所以在相同荷载下，预应力筋变形增大，体外预应力筋的应力增量增大。

分析图12可以看出：波形钢腹板厚度与梁高的比值对预应力筋应力增量的影响很小。

5 结论

本研究开展了体外预应力波形钢腹板组合梁的模型试验，基于变形理论推导了波形钢腹板组合梁弹性阶段体外预应力筋应力增量的解析解公式，得出以下结论：

①在弹性阶段，“二次效应”对体外预应力筋应力增量的影响为0.2 %，可以忽略不计。

②在弹性阶段，体外预应力筋应力增量随混凝土弹性模量的增加而线性减小，随梁高的增加而线性增加；波形钢腹板厚度与梁高的比值对预应力筋应力增量的影响很小。

③推导的弹性阶段考虑“剪切变形”和“二次效应”的体外预应力筋应力增量计算公式与试验结果吻合较好，可用于波形钢腹板组合梁的体外预应力设计。