南宁地铁盾构双线隧道地表沉降预测模型研究
23
(1.广西大学土木建筑工程学院, 广西南宁530004;2.工程防灾与结构安全教育部重点实验室, 广西南宁530004;3.广西金属尾矿安全防控工程技术研究中心, 广西南宁530004)
0 引言
众多隧道工程实例表明,无论采取何种施工方法都不可避免地造成土层的扰动变形,影响隧道周边地表、建筑物与地下管线的安全,而城市地铁隧道作为主要的交通线路,一般都从城市的重要区域穿过,因此研究地铁隧道施工对周边环境的影响意义重大。目前,对单线隧道施工引起的地表沉降研究已有很多,而对双线隧道施工引起的地表沉降研究则相对较少。Peck公式是基于大量实测资料提出的预测单线隧道沉降槽的经验公式,韩煊等[1-2]对Peck公式进行了深入的工作,其后仍有许多学者对Peck公式进行了不同形式的修正以提高其适用性。ATTEWELL等[3]将一条隧道开挖产生的地表沉降与另一条隧道开挖产生的地表沉降进行叠加,从而总结出双圆平行隧道开挖产生的地表沉降表达式,由于缺乏对两平行隧道之间的相互影响进行考虑,地表沉降预测误差较大。SAGASETA[4]基于peck公式,考虑两条隧道之间的相互影响,引入补偿参数的概念,采用偏移参数法改进了双线隧道施工地表沉降的预测公式,使得预测更准确,但只适用于隧道地表横向沉降槽的形状大致对称只是存在中心偏移的情况。HUNT[5]通过二维有限元计算分析得到用于计算地表及以下土体位移的修改函数,考虑对第二条隧道施工引起的地表沉降进行修正,提出了一种改进的预测双线隧道地表沉降曲线的方法。该方法虽然更接近双线隧道现场施工的实际情况,但操作过程相对复杂,工作量较大。
根据南宁地铁某盾构区间隧道的实际监测资料,在分析总结该双线隧道地表横向沉降规律与地表沉降历时变化规律的基础上,考虑双线隧道左右线先后开挖的相互影响,确定了左右线之间的沉降影响范围,基于Peck沉降槽理论,提出了一种预测地铁双线隧道盾构施工引起地表沉降的新思路与新方法,并总结得到预测模型。
1 工程概况
南宁地铁2号线工程为南北走向,建设范围从玉洞至西津,全程均为地下线,约20.8 km;共设18座车站,均为地下站。该区间为金象站至石子塘站,线路沿银海大道地下敷设,两旁民宅较多,距离区间最近处9.70 m。本区间隧道为双线圆形盾构隧道,全长1198.086 m,线间距12.0~14.0 m,曲线最小半径为450 m;结构底板埋深为14.9~21.3 m,底板高程为72.80~84.93 m。区间范围内岩溶较发育,分布有灰岩、泥灰岩等可溶岩地层,在灰岩、泥灰岩的表层常见有溶孔、溶蚀裂隙,部分方解石充填;初、详勘阶段共有26个钻孔揭示灰岩,其中有5个钻孔发现有溶洞,遇洞率约19.23 %。溶洞大小不一,钻孔中揭示溶洞高度0.30~3.10 m,均为充填性溶洞,充填物为黏土、粉质黏土,少量砂和砾砂。
2 监测点布置及沉降规律分析
2.1 监测点布置
本区间监测等级为二级,监测点沿盾构隧道轴线上方地表布设,纵断面测点间距在始发和接收端间距为10 m,其余间距为25 m。横断面间距50 m,必要时加密为5 m,监测点数量为9个,主要影响区的监测点间距为3~5 m,次要影响区的监测点间距为5~10 m。监测点平面布置如图1所示。
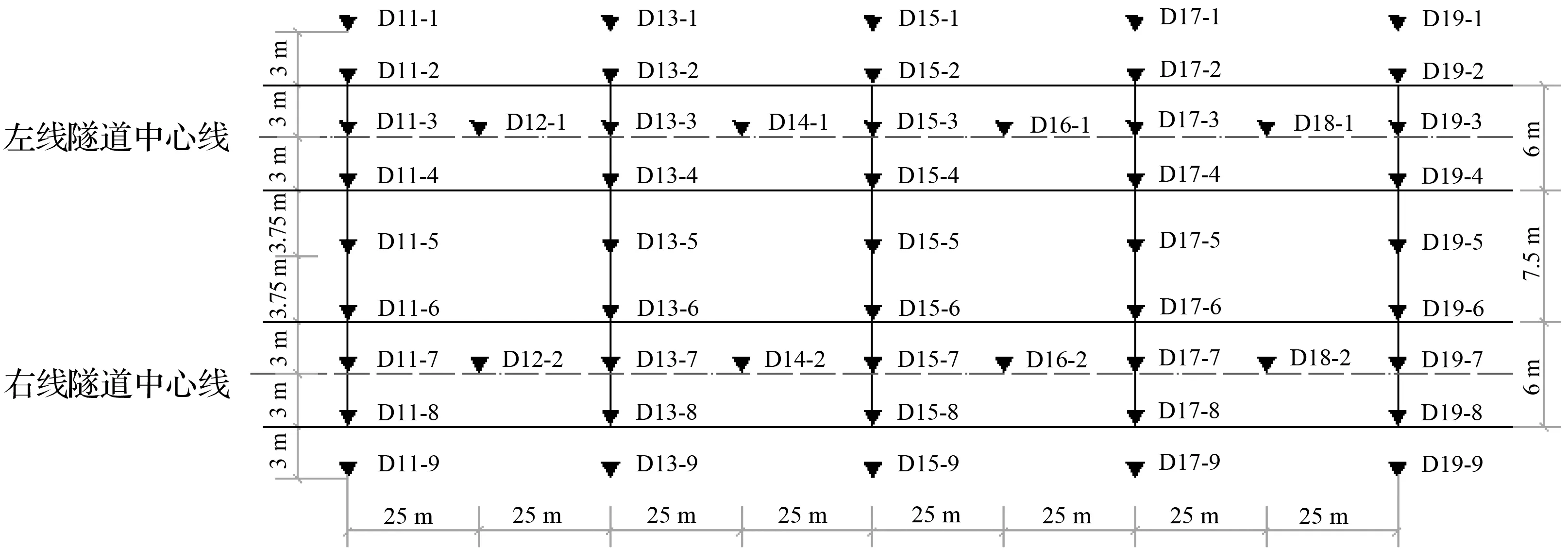
图1 监测点平面布置图Fig.1 Layout plan of monitoring points
本文主要研究隧道沿线Z(Y)DK220+195、Z(Y)DK220+245、Z(Y)DK220+295、Z(Y)DK220+345、Z(Y)DK220+395等5个横断面,断面编号分别为11、13、15、17与19,通过分析其横、纵向的地面沉降分布变化来了解隧道开挖引起地表沉降的特征。
2.2 地表沉降规律分析
以横断面13为例,隧道埋深约为10 m,直径6 m,隧道中心间距为13.5 m,左线隧道先开挖,右线隧道滞后左线隧道开挖约150环,双线隧道地表横向沉降变化情况与监测时间的关系如图2所示,监测时间从2015年8月16日至2015年9月14日(8.16表示为8月16日),8月20日左线隧道盾构施工到达监测掌子面,9月6日右线隧道盾构施工到达监测掌子面。

图2 断面13地表横向沉降曲线Fig.2 Transverse surface settlement curve of section 13
由图2可知,左线隧道盾构掘进通过后,横断面上的地表沉降曲线基本表现为正态分布,左线隧道开挖范围内对应地表最大沉降为41.6 mm,右线隧道中心线正上方地表中心处沉降为10.7 mm;双隧道盾构掘进完成后,左线隧道轴线正上方地表中心处最大沉降为49.7 mm,右线隧道轴线正上方地表中心处沉降为35.2 mm。双隧道地表最终总沉降曲线类似于两条并行的单线隧道分别独立开挖引起的沉降通过叠加得到,沉降槽曲线明显被拉宽加深,但表现出左右不对称的形状[6-7]。该双线隧道的隧道中心间距与隧道埋深比值D/H小于3,大量工程实例表明,此时两条隧道一定会对彼此的施工产生影响,两条隧道之间的相互干扰不可以忽略[8],因此在影响范围之内的地表就会产生较大的叠加沉降及变形,使得沉降槽变宽加深;地表沉降槽出现不对称性的原因较复杂,涉及左右线地质情况与盾构施工参数等方面,结合众多学者的研究,可以认为是左右线隧道施工对彼此的相互影响程度不一致造成的。由于先开挖隧道及时进行管片支护并注浆加固,使得先开挖隧道范围内的土层刚度大大提高,后开挖隧道对先开挖隧道的地表沉降影响相对先开挖隧道对后开挖隧道的地表沉降影响较小,因此后开挖隧道一侧的地表沉降一般略大于先开挖隧道一侧的地表沉降[9]。然而在该研究区间的地表沉降曲线的左右分布情况刚好相反,笔者通过分析发现其原因有二:(1)区间左线岩溶发育较之右线强烈,地层稳定性较差,故先开挖的左线隧道一侧地表竖向变形较明显;(2)左线隧道先开挖,右线隧道滞后约150环开挖,施工单位总结相同地段左线开挖的成功经验,改进右线盾构施工方法,降低了右线隧道盾构施工对地表沉降的影响,即右线开挖引起的地层损失相对左线开挖引起的地层损失明显要小,最终整体的地表总沉降曲线表现为左侧大右侧小的分布,符合现场实际情况。
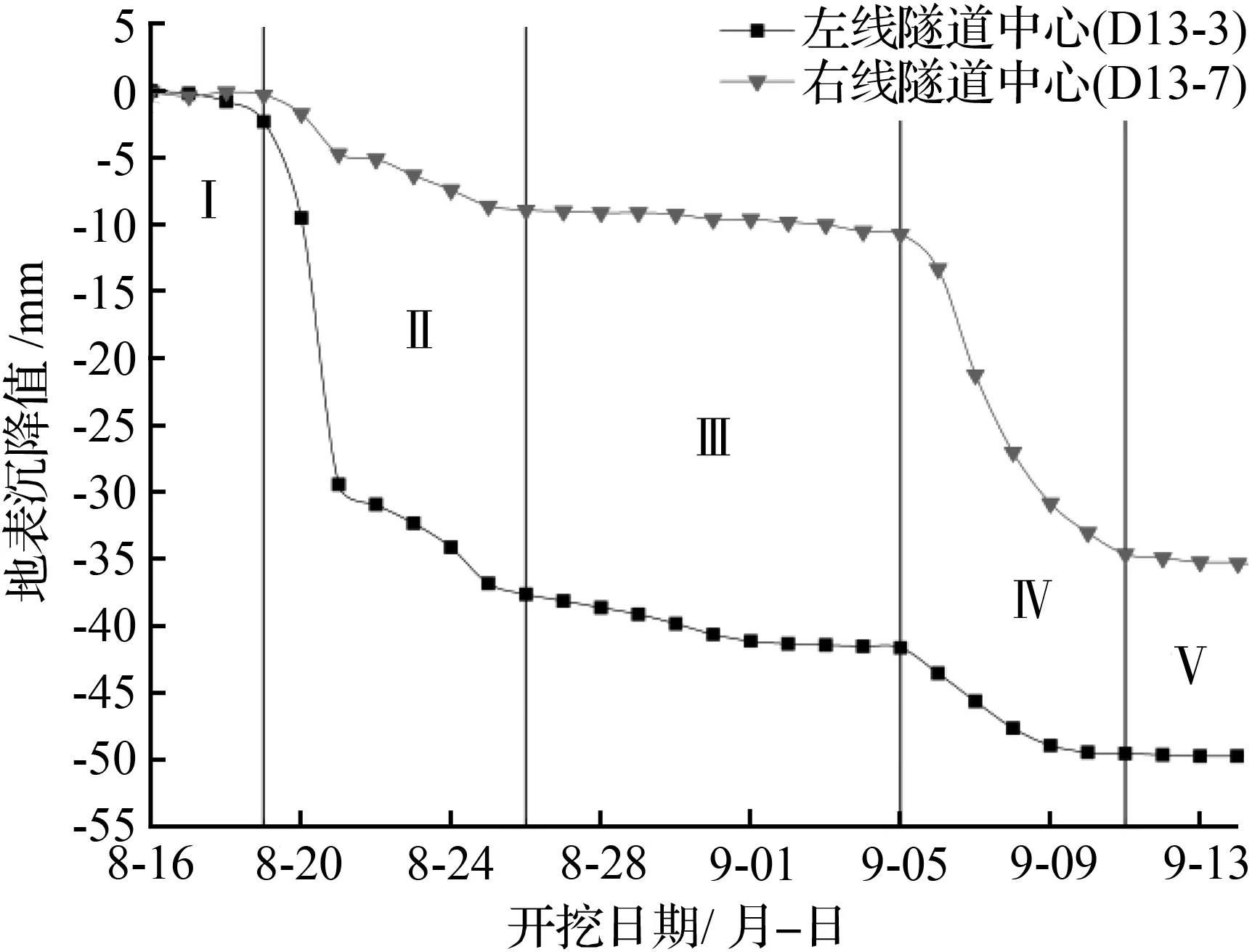
图3 左、右线隧道中心点地表沉降历时曲线Fig.3 Curve of the surface settlement of the center of the left and right tunnel
图3详细地描绘出两隧道中心线对应的地表点随着隧道不断开挖而造成的沉降变化情况,D13-3、D13-7分别为左、右线隧道中心地表沉降监测点。观察图3中左、右线隧道中心的地表随隧道开挖过程(时间)的沉降变形情况,可以将双线隧道盾构先后施工引起的地表沉降划分为5个阶段[10]。Ⅰ初期沉降阶段:当盾构开挖面距离监测断面还很远,盾构开挖引起的地层损失对监测断面附近的影响甚微,此时左、右线隧道地表沉降均很小,主要是降水施工引起的土体固结变形。Ⅱ左线盾构接近阶段:随着左线隧道的开挖,盾构掌子面不断逼近监测断面,断面地层应力得到释放,围岩土体松动变形较大,左线隧道地表沉降加速,沉降槽逐渐成形,期间也伴随着岩溶地质的土层固结变形;右线隧道地表在左线盾构施工的影响下也产生了一定的沉降变形。Ⅲ左线盾构远离、右线盾构接近阶段:左线隧道穿越监测断面,初期衬砌结构施工完成后,左线隧道地表沉降变形发展缓慢;右线隧道盾构掌子面距离监测断面尚远,对监测断面土体影响微小,右线隧道地表沉降变形发展也十分缓慢。Ⅳ右线盾构接近阶段:随着右线隧道的开挖,盾构掌子面不断逼近监测断面,右线隧道地表急剧沉降变形,同时引起左线隧道地表再次产生一定程度的下沉。Ⅴ右线盾构远离、沉降变形稳定阶段:最后右线隧道也盾构通过并逐渐远离监测断面,盾构管片安装完毕并及时进行注浆后,双线隧道的地表沉降槽也基本趋于稳定,工后围岩土体的固结变形缓慢,地层状态恢复稳定[11]。
3 地表沉降预测模型的建立与验证
3.1 Peck沉降槽理论
Peck通过对大量工程实测数据的分析处理,发现单隧道施工引起的地表横向沉降曲线满足正态分布,并拟合得到计算公式。ATTEWELL等[3]在此基础上进一步研究,将计算公式简化如下:
(1)
式中,Smax为最大沉降值,位于沉降曲线对称点上,即单隧道中心轴线对应的地表沉降量,根据地层损失率、隧道掌子面面积以及沉降槽宽度的关系计算得到;x为沉降计算点到坐标原点的水平距离,坐标原点为隧道中心轴线对应地表点;i表示沉降曲线上对称点与拐点之间的水平距离,定义为沉降槽宽度。
3.2 建立预测模型的总体思路
首先,基于沉降槽Peck公式及O’Reilly和New最大沉降与隧道埋深的关系,采用数值分析软件origin对现场地表沉降监测数据进行拟合分析,得到地铁盾构隧道单线独立沉降槽的宽度和最大沉降。其次,考虑双线隧道盾构施工的相互影响,引入左右线之间的相互影响系数,提出这两个影响系数的确定方法,并通过影响系数确定双线隧道施工引起地表沉降的相互影响范围。然后,运用相互影响系数对左右线隧道地表沉降公式进行修正,将相互影响范围内的修正后的左右线隧道地表沉降曲线相互叠加。最后提出一种采用分段函数形式表达的地铁盾构双线隧道施工引起地表沉降的预测模型。
3.2.1 左右线单隧道地表独立沉降Peck曲线拟合
纵观学者们对地铁隧道施工引起的地表沉降预测的研究,结合上节对双隧道施工引起的地表沉降规律的分析,同时考虑到双隧道施工顺序一般为一线先行开挖另一线保持一定距离后开挖,对于任一断面而言始终只有一条隧道是正在开挖通过,因此不难发现双隧道施工引起的地表沉降与左、右线单隧道独立施工引起的地表沉降有着密不可分的联系[12]。因此本文建立在左右线单隧道地表独立沉降的基础上,通过对其进行一系列的修正、叠加而得到的双线隧道地表沉降预测模型是与工程实际紧密结合的,具备一定的合理性。
由上节对双线隧道的沉降规律分析可知,在Ⅲ左线盾构远离、右线盾构接近阶段前,左线隧道施工引起的地表沉降是相对独立的,对应的监测数据可认为没有受到右线隧道施工的干扰[13],故可将Ⅱ左线盾构接近阶段末的左线隧道区域内的地表沉降监测点的监测数据采用Origin软件通过Peck公式进行拟合得到的表达式作为左线单隧道地表独立沉降公式。右线隧道后行开挖,右线隧道区域内的地表沉降已经受到左线隧道施工的干扰,监测数据无法实现真正的独立,在这里采用右线隧道区域内地表最终总沉降值减去Ⅱ左线盾构接近阶段末由于左线隧道施工引起的右线隧道区域内的地表沉降值的方法近似得到右线单隧道地表独立沉降值[14],同理通过Peck公式拟合得到右线单隧道地表独立沉降公式。
图4为监测断面13左线单隧道地表独立沉降Peck曲线拟合图,相应的Smax=-42.13,i=4.88,相关系数为0.996,拟合效果好。图5为监测断面13右线单隧道地表独立沉降Peck曲线拟合图,相应的Smax=-22.74,i=5.00,相关系数为0.781,拟合效果较好。
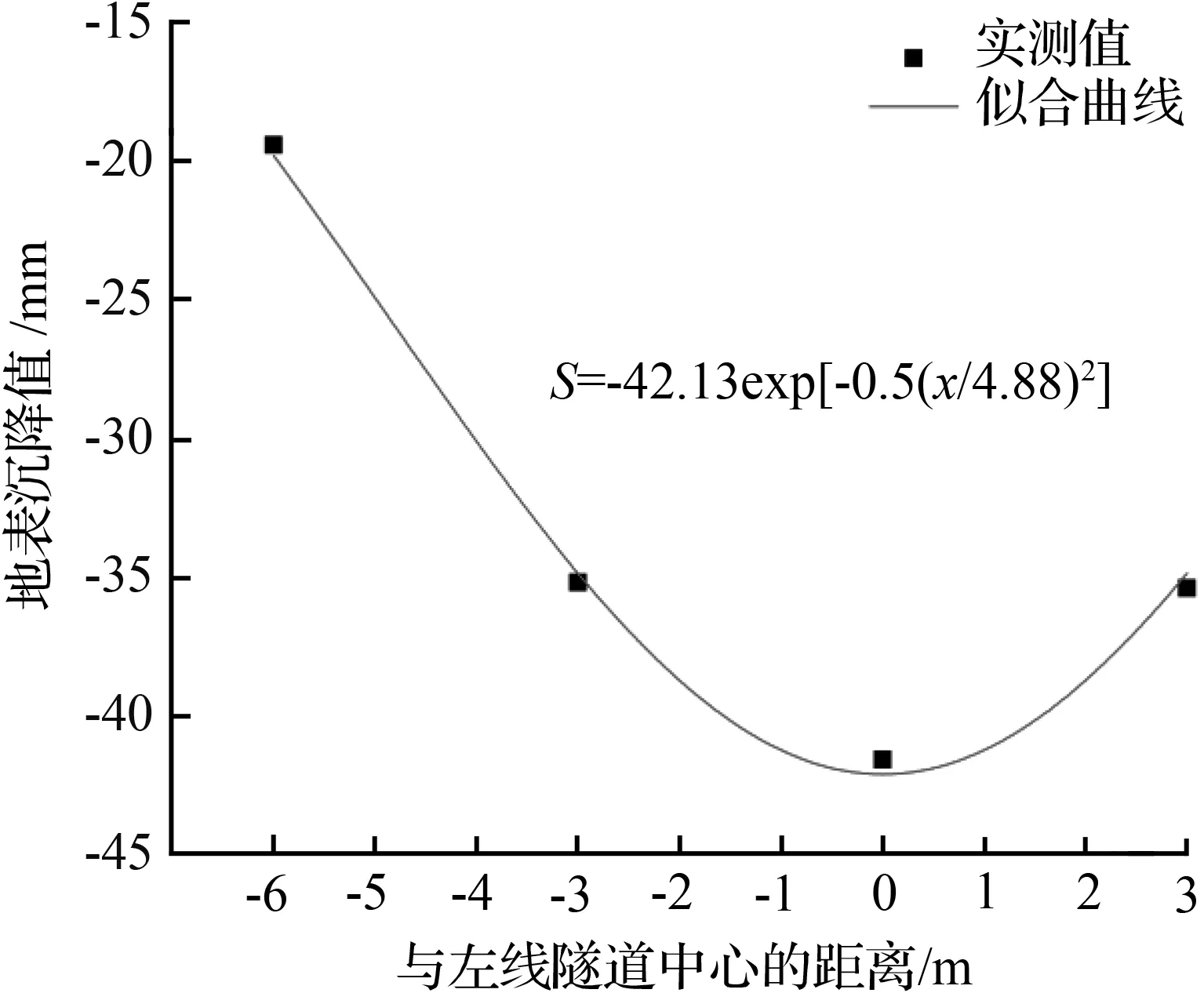
图4 左线单隧道地表独立沉降Peck曲线拟合
Fig.4 Peck curve fitting of surfacesettlement of left tunnel

图5 右线单隧道地表独立沉降Peck曲线拟合
Fig.5 Peck curve fitting of surfacesettlement of right tunnel
由此可得,监测断面13左、右线单隧道地表独立沉降公式分别为:
(2)
(3)
3.2.2 相互影响系数及相互影响范围的确定方法
在地铁双线隧道先后开挖的过程中,当双线隧道的间距较近,其中一条隧道的开挖必然会对另一条隧道区域内的地表沉降产生影响,故可引入关于左右线隧道地表沉降的相互影响系数的概念,即左线隧道施工对右线隧道地表沉降影响系数和右线隧道施工对左线隧道地表沉降影响系数。从宏观的角度来看,相互影响系数是双线隧道盾构施工地表沉降的各种影响因素的综合表现,其大小与双线隧道的间距、左右线先后开挖顺序与间隔、盾构施工参数对地层的影响以及隧道周边地质情况等有关。本次相互影响系数的确定方法主要是从宏观上对双线隧道盾构施工地表沉降各阶段之间的关联规律进行总体考虑,相互影响范围根据相互影响系数确定。

图6 双线隧道中心区域地表监测点的纵向沉降曲线Fig.6 Vertical settlement curve of ground monitoring points in the central area of double tunnel
双线隧道中心点连线范围内是相互影响的主要区域,图6为双线隧道中心区域地表监测点的纵向沉降曲线图,分析曲线的规律可知它们之间存在一定的关联性:在Ⅱ左线盾构接近阶段,左线隧道施工主导地表沉降的产生与发展,然后带动右线隧道区域内的地表随着左线隧道区域内的地表沉降而沉降,且越靠近左线隧道中心地表沉降发展越快;同理,在Ⅳ右线盾构接近阶段,右线隧道施工主导地表沉降的产生与发展,然后带动左线隧道区域内的地表随着右线隧道区域内的地表沉降而沉降,且越靠近右线隧道中心地表沉降发展越快。据此可将左线隧道施工对右线隧道地表沉降影响系数定义为Ⅱ阶段中心区域各点的地表沉降变化值与左线隧道中心点的沉降变化值之比,即FLR=SR2/SL2,将右线隧道施工对左线隧道地表沉降影响系数定义为Ⅳ阶段中心区域各点的地表沉降变化值与右线隧道中心点的沉降变化值之比,即FRL=SL4/SR4,再结合相应的位置坐标关系,采用线性拟合的方式,便可建立起相互影响系数的函数关系表达式。
如图7、图8所示,左线隧道施工对右线隧道地表沉降影响系数为:
FLR=-0.0544x+0.308。
(4)
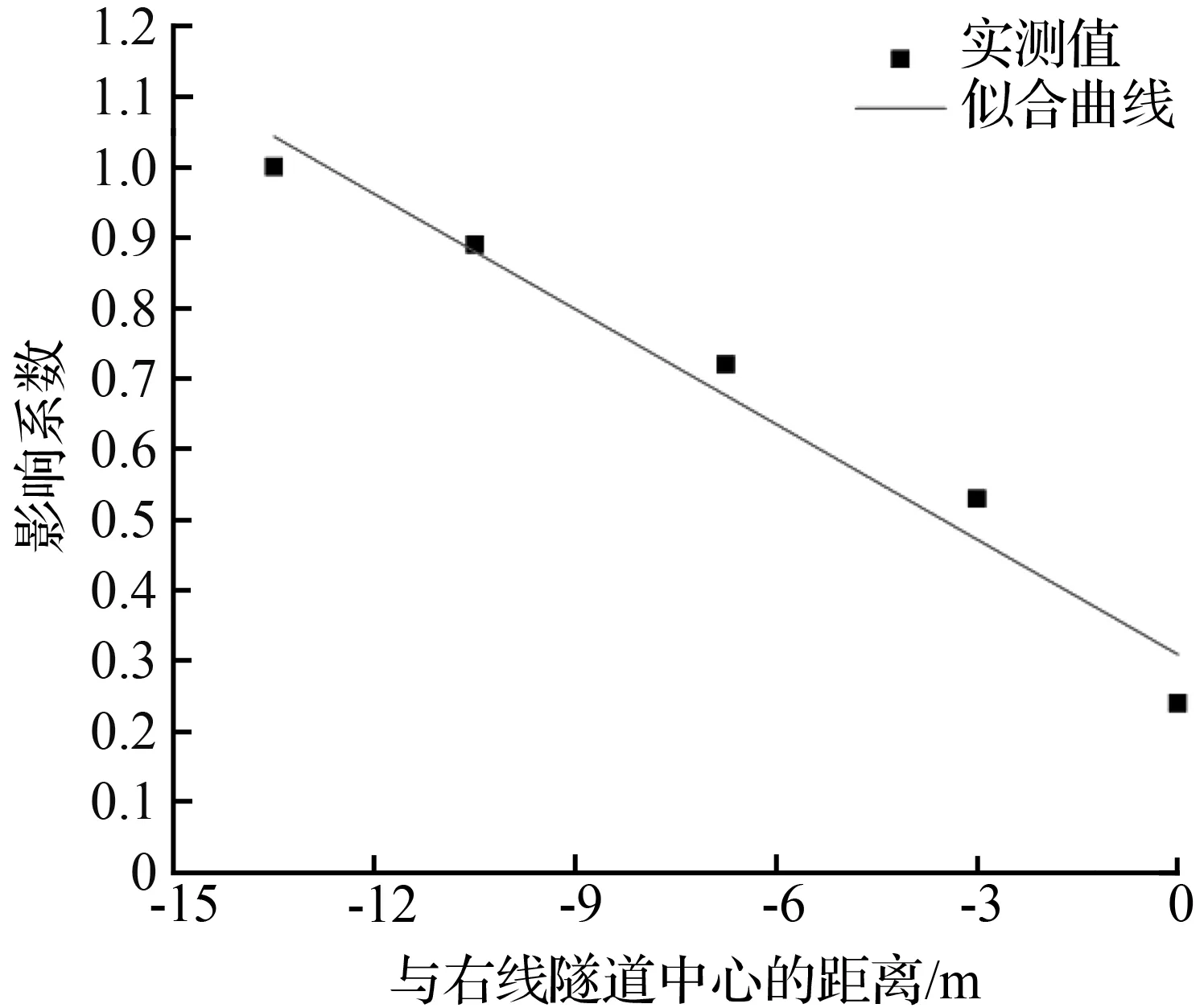
图7 左线隧道施工对右线隧道地表沉降影响系数拟合
Fig.7 Influence coefficient fitting of the left tunnelconstruction on the surface settlement of the right tunnel
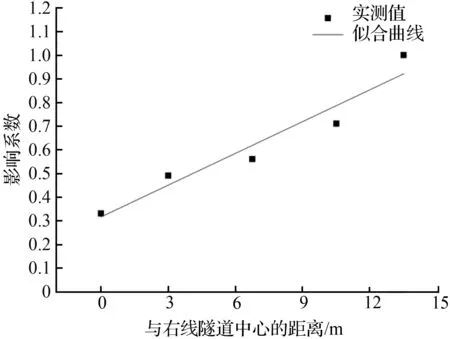
图8 右线隧道施工对左线隧道地表沉降影响系数拟合
Fig.8 Influence coefficient fitting of the right tunnelconstruction on the surface settlement of the left tunnel
右线隧道施工对左线隧道地表沉降影响系数为:
FRL=0.0446x+0.3173。
(5)
当双线隧道的间距较远时,双线隧道地表沉降的相互影响很小甚至可忽略不计[15],结合相互影响系数的定义,引进相互影响范围这一概念,在相互影响范围内相互影响系数的大小随地表位置坐标变化而变化,在相互影响范围外相互影响系数为0。由图7、图8可知,令左线隧道施工对右线隧道地表沉降影响系数为0,则可确定相互影响范围的右边界,令右线隧道施工对左线隧道地表沉降影响系数为0,则可确定相互影响范围的左边界,若以双线隧道中心为坐标原点,则断面13的相互影响范围为(-13.86,12.41)。
3.2.3 左右线隧道地表沉降公式的修正方法
由上章对地表纵向沉降规律的分析,双线隧道盾构施工引起的地表沉降可划分为Ⅰ初期沉降阶段、Ⅱ左线盾构接近阶段、Ⅲ左线盾构远离、右线盾构接近阶段、Ⅳ右线盾构接近阶段以及Ⅴ右线盾构远离、沉降变形稳定阶段,具体可用数学公式表达为:
(6)
(7)
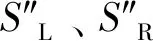
从图3可知,双线隧道地表沉降主要发生在Ⅱ、Ⅳ阶段,Ⅰ、Ⅲ、Ⅴ阶段的地表沉降变化缓慢,且沉降量占总沉降量的比例很小。对比双线隧道地表沉降规律与单隧道地表沉降规律,我们不难发现,双线隧道中的左线隧道地表沉降相当于在左线单隧道地表独立沉降的基础上加上Ⅳ阶段的右线单隧道地表独立沉降的影响,同理双线隧道中的右线隧道地表沉降相当于在右线单隧道地表独立沉降的基础上加上Ⅱ阶段的左线单隧道地表独立沉降的影响。即:
(8)
(9)
(10)
(11)

根据上节对相互影响系数的定义,左线隧道施工对右线隧道地表沉降影响系数为:FLR=SR2/SL2,右线隧道施工对左线隧道地表沉降影响系数为:FRL=SL4/SR4,故在相互影响范围内,双线隧道中的左线隧道地表沉降修正公式、右线隧道地表沉降修正公式分别为:
(12)
(13)
上述修正公式表达的实际意义为:双线隧道施工引起的地表沉降中,在相互影响范围内的左线隧道区域内的地表沉降由两部分组成,第一部分为在左线隧道区域内先独立开挖左线隧道引起的沉降值,第二部分为右线隧道施工影响的沉降修正值。修正部分沉降相当于在原来左线隧道区域内按照右线隧道的施工模式开挖引起的沉降,且沉降的影响程度由相互影响系数决定。由于左、右线隧道在空间上的对称性,右线隧道区域内的地表沉降与左线隧道区域内的地表沉降同理。
将上述修正公式运用到断面13,可得双线隧道中的左线隧道地表沉降修正公式、右线隧道地表沉降修正公式分别为:
(14)
(15)
修正后的左、右线隧道地表沉降曲线如图9所示。
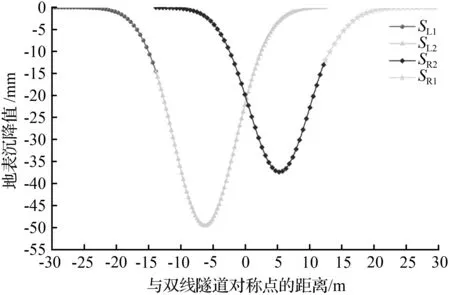
图9 修正后的左、右线隧道地表沉降曲线Fig.9 Surface settlement curve of the left and right tunnel after correction
3.2.4 双线隧道地表总沉降预测表达式
以断面13为例,结合上述理论分析成果可知双线隧道地表总沉降的预测表达式为分段函数,具体按照区域划分为三段:①在相互影响范围外的左线隧道区域内的地表沉降预测表达式;②在相互影响范围内的修正后的左右线隧道地表沉降相互叠加后的沉降预测表达式;③在相互影响范围外的右线隧道区域内的地表沉降预测表达式。即双线隧道地表总沉降的预测表达式为:
(16)
观察图10,对比双线隧道地表总沉降的预测曲线与实测值,两者吻合度较高,地表沉降预测效果良好。

图10 断面13双线隧道地表总沉降的预测曲线与实测值Fig.10 Prediction curve and the measured value of the total settlement of the double tunnel of section 13
3.3 地表沉降预测模型
基于Z(Y)DK220+245,断面13的双线隧道地表沉降规律分析和双线隧道地表总沉降预测表达式的推导,针对土压平衡盾构隧道施工工法,本文总结出如下双线隧道地表沉降预测模型:
(17)
(18)
(19)
(20)
式中:S1为在相互影响范围外的左线隧道区域内的地表沉降;
S2为在相互影响范围内的修正后的左右线隧道地表沉降相互叠加后的沉降;
S3为在相互影响范围外的右线隧道区域内的地表沉降;
x1、x2分别为相互影响范围的左边界、右边界,由相互影响系数确定;
SmaxL、iL分别为左线隧道独立沉降的最大沉降的理论值与沉降槽宽度;
SmaxR、iR分别为右线隧道独立沉降的最大沉降的理论值与沉降槽宽度;
FRL为左线隧道施工对右线隧道地表沉降影响系数;
FLR为右线隧道施工对左线隧道地表沉降影响系数;
D为双线隧道中心间距。
预测模型以双线隧道对称点为坐标原点,各参数具体的确定方法参见上节建立预测模型的总体思路。
3.4 计算与实测结果对比分析
前三节通过对研究区间隧道断面13的地表沉降分析,提出了一种采用分段函数形式表达的地铁双线隧道盾构施工引起地表沉降的预测模型。下面运用此预测模型理论分别对另外4个断面各参数进行计算,从而确定各断面的地表沉降预测模型表达式。断面11、断面15、断面17和断面19的预测模型参数如表1所示。

表1 不同断面的预测模型参数Tab.1 Prediction model parameters of different sections
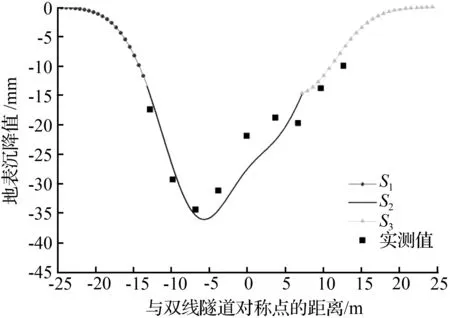
运用该预测模型的分析计算方法,利用各断面的预测模型参数可以作出各断面双线隧道地表总沉降的预测曲线与实测值对比图,如图11所示。可以发现,与断面13一样,断面11、断面15、断面17和断面19的地表沉降预测模型计算所得结果与现场实际监测最终沉降结果均具有较高的吻合性,说明该方法在很大程度上是合理的,由此也可验证预测模型的可靠性。今后在类似的地铁盾构双线隧道工程可以采用该预测模型对地表沉降进行预测,即对工程前期盾构过程中某个具有地质条件代表性的盾构区间选取典型断面进行预测模型参数计算,从而得到有参考价值的地表沉降预测模型,进而可以预估整个盾构区间的地表沉降情况,这对施工过程中盾构参数的调整、地表沉降的控制以及工程灾害事故的预防等方面都起到很重要的指导作用。

(a) 断面11

(b) 断面15
(c) 断面17

(d) 断面19
图11 双线隧道地表总沉降的预测曲线与实测值
Fig.11 Prediction curve and the measured value of the total settlement of the double tunnel
4 结论
①依托南宁地铁2号线土压平衡盾构施工的双线隧道,通过对施工现场地表沉降的监测分析,揭示了双线隧道左、右线先后开挖过程中的地表横向沉降规律,以及左、右线隧道中心点地表沉降变形的历时变化规律。
②结果表明,隧道中心点地表沉降变形可划分为五个阶段:Ⅰ初期沉降阶段,Ⅱ左线盾构接近阶段,Ⅲ左线盾构远离、右线盾构接近阶段,Ⅳ右线盾构接近阶段,Ⅴ右线盾构远离、沉降变形稳定阶段;左、右线沉降槽曲线基本满足高斯分布,双线沉降槽曲线可由左、右线沉降槽曲线修正后叠加组合得到。
③基于沉降槽Peck公式,考虑双线隧道先后开挖的相互影响,引入左线隧道施工对右线隧道地表沉降影响系数和右线隧道施工对左线隧道地表沉降影响系数,并提出这两个影响系数的确定方法,对相互影响范围内的双线隧道地表沉降公式进行修正,从而提出了一种采用分段函数形式表达的地铁双线隧道盾构施工引起地表沉降的预测模型。
④该预测模型是在分析总结地铁双线隧道盾构施工现场地表沉降监测数据的基础上提出的,根据施工前期某几个代表断面可确定模型参数取值,从而对之后的地表沉降进行预测,这对施工过程中盾构参数的调整、地表沉降的控制以及工程灾害事故的预防等方面都起到很重要的指导作用。其总体思路与分析方法具有一般性,今后在运用时需针对不同地区地层特性进一步完善预测模型,提高其适用性与准确性。

