无人机导航信号的增强及干扰抑制技术

孙彦景，陈功骁，张 亮，李 松

中国矿业大学信息与控制工程学院，江苏徐州 221116

近年来，无人机(unmanned aerial vehicle, UAV)已被广泛用于侦察、测绘及勘探等领域[1-3]．全球卫星导航系统可为无人机提供全天候、实时的位置信息，对无人机导航起着至关重要的作用．无人机导航经常受到干扰的影响，这些干扰由大功率的干扰机故意投送，其功率大且覆盖范围广，导致采用单天线接收机的无人机导航无法正常进行．多天线卫星导航接收机采用自适应波束形成技术．经典的自适应波束形成以最小方差无失真响应(minimum variance distortionless response, MVDR)波束形成为代表，在保证信号无失真通过的条件下最小化阵列输出功率，实现信号增强以及对干扰和噪声的有效抑制．无人机导航中遇到的干扰具有高动态特性，传统的自适应波束形成技术在干扰快速运动环境中性能退化严重．近年来欺骗干扰技术被用于合成孔径雷达(synthetic aperture radar, SAR)虚假目标成像中，通过对SAR信号的截获、调制和转发，并在SAR接收数据中添加虚假目标，达到混淆的目的[4-5]．一旦该技术被用于无人机导航干扰，多天线导航接收机将无法获得可靠的位置信息[6]．另外，获取高信噪比的卫星导航信号要求接收机天线阵列具有较大的孔径，但是大孔径天线阵列也带来了成本上升和布放困难的问题．因此，研究具有快速运动干扰抑制功能的高增益波束形成技术对于无人机导航尤为迫切必要．

零陷展宽技术能保证加权向量应用期间干扰始终处于零陷内，提高了自适应波束形成器抗干扰的稳健性．MAILLOUX[7]利用多个离散虚拟干扰源代替原来的点干扰源，推导加入虚拟干扰源后的数据协方差矩阵，并基于MVDR波束形成获得了零陷展宽的波束图．ZATMAN[8]提出利用带通干扰代替原窄带干扰的零陷展宽方法，该方法与MAILLOUX方法本质上是一致的，但不会改变数据协方差矩阵中噪声项的特性，且展宽后的零陷更平坦．GUERCI等[9]提出协方差矩阵锐化(covariance matrix taper, CMT)的波束零陷展宽方法，将MAILLOUX和ZATMAN的方法统一了起来．该方法的运算复杂度低，但是零陷深度较浅不利于强干扰源的抑制．对预设区域的波束输出功率进行二次约束(quadratic constraint sector suppressed, QCSS)可获得深度较深的展宽零陷[10]，ZHANG等[11]针对二次约束优化求解复杂度高的问题，提出低复杂度的线性约束(linear constraint sector suppressed, LCSS)零陷展宽方法．

经典的自适应波束形成方法采用最小方差准则，仅利用了信号的二阶统计特征，忽略了高阶和分数阶统计特征对波束形成性能的影响．实际中无人机导航信号呈现非高斯分布特点，利用信号的统计特性可改善波束形成器的性能．针对非高斯信号，高阶统计量能有效提取信号的统计信息．在自适应波束形成器设计中，对高阶统计量的研究集中在四阶累积量及其三谱方面．利用加性高斯白噪声四阶累积量为零的特点，可实现高斯白噪声中非高斯信号的提取，另外四阶累积量具有虚拟阵列扩展功能，可有效扩大阵列孔径[12]．但是，基于高阶统计量的方法仅利用了信号有限阶统计特征，忽略了更高阶和分数阶统计特征对波束形成性能的影响．JIANG等[13]将阵列输出数据p范数最小化方法应用到通信信号波束形成中．从统计学的观点来看，该方法将最小方差准则推广为更适用于次高斯分布的最小离差准则，由于联合了信号的高阶统计特征，提升了波束形成器的性能．但该方法在设计过程中并未考虑到高动态干扰源的影响，不能直接用于多天线卫星导航接收机中．

针对无人机导航中高动态干扰抑制问题，本研究结合多天线导航接收机，提出一种高增益的稳健波束形成方法．该方法遵循最小离差准则，利用导航信号的非高斯特性获得高增益的波束输出，并在此基础上建立预设角度区间内干扰平均功率的约束条件，克服了高动态干扰给无人机导航带来的不利影响．提出的波束形成器可通过解算带有二次约束的凸优化问题获得，将用一个线性约束替换二次约束，不仅降低了运算复杂度，还可提升干扰抑制效果．

1 问题描述

1.1 信号模型

假设远场区域存在K个不相干的信号源，采用M元天线阵列对信号进行接收，则第t个时刻天线阵列接收到的数据为

x(t)=α(θ0)s0(t)+

(1)

其中，θ0为期望信号(signal-of-interest, SOI)的方位角(direction-of-arrival, DOA)；θk为第k个干扰源的方位；α(θ0)和α(θk)分别对应目标和干扰的导向向量；n(t)为加性噪声；s0(t)为目标辐射信号；sk(n)为干扰信号.以均匀线列阵为例，干扰的导向向量可表示为

α(θk)=[1, ej(2π/ξ)dsinθk, ej2(2π/ξ)dsinθk, …,

ej(M-1)(2π/ξ)dsinθk]T

(2)

其中，ζ为波长；d为天线间距；M为天线数量．

1.2 MVDR波束形成

波束形成器的输出为

y(t)=wHx(t)

(3)

其中，w为波束形成权向量； H为共轭转置运算符．

波束形成器的输出信干噪比(signal-to-interference-plus-noise ratio，SINR)为

(3)

MVDR波束形成器在保证期望信号不失真的条件下最小化波束输出功率，实现对干扰和噪声的有效抑制，对应的优化问题可表示为

(5)

MVDR波束形成器权向量形式为

(6)

实际中干扰和噪声的协方差矩阵都是未知的，一般通过数据采样进行替换．数据采样协方差矩阵的计算式为

(7)

其中，N为快拍数．则MVDR波束形成器加权向量形式修正为

(8)

式(8)是基于采样协方差矩阵逆(sample matrix inverse, SMI)算法的加权向量．

1.3 最小功率无畸变响应波束形成

假设快变干扰源的方位角在预设区间[θL,θU]内服从均匀分布．最小功率无畸变响应波束形成(minimum power distortionless response, MPDR)约束[θL,θU]的功率输出小于一个常数，并在波束图对应的区域产生一个凹槽，实现对快变干扰的抑制．MPDR波束形成器可表示为

(9)

其中，η是一个经验常数，用来控制凹槽的深度；

(10)

其中，α(θ)为干扰的导向向量；θ∈[θL,θU].

1.4 最小离差无失真响应波束形成

零均值随机信号的峰态值定义为

(11)

按照峰态值的不同，随机信号s(t)被划分为3种类型：当κs>3时，s(t)为超高斯信号；当κs=3时，s(t)为高斯信号；当κs<3时，s(t)为次高斯信号．

超高斯信号主要包括Laplace分布和α稳态分布，次高斯分布主要包括均匀分布和贝努力分布．人类的语音信号是一种典型的超高斯信号．通过调制获得的通信信号、雷达、声纳和卫星导航信号都属于次高斯信号．

最小离差无失真响应(minimum dispersion distortionless response, MDDR)波束形成器通过阵列输出数据p范数最小化实现，由于联合了信号的各阶统计特征，可以提升非高斯信号的接收性能[10]．针对次高斯信号的MDDR波束形成可表示为

(12)

其中，X=[x(1),x(2), …,x(N)]，N为快拍数．

2 稳健MDDR波束形成

高动态干扰环境中MDDR波束形成器性能急剧下降，需要在干扰源可能存在的方位设置零陷凹槽，提高MDDR抗干扰的稳健性．

假设快变干扰的方位角在[θL,θU]内服从均匀分布，其概率密度函数为

(13)

其中， ΔθI为快变干扰的方位角.

受MPDR波束形成器的启发，对高动态干扰进行抑制可通过限制[θL,θU]内波束输出功率获得．稳健的MDDR波束形成器可表示为

(14)

其中，QNull为埃尔米特矩阵，

(15)

MDDR波束形成器在[θL,θU]的平均功率输出为

(16)

令η=0， 并对矩阵QNull进行特征分解，稳健的MDDR波束形成可进一步表示为

(17)

其中，V=[α(θ0), Vr]，e1=[1, 0T]T，Vr是QNull张成空间R(QNull)的正交基．与式(14)相比，式(17)的约束条件为线性约束，解算效率更高．式(14)中约束条件η在式(17)中更新为0，由式(17)获得的凹槽深度更深．

3 基于牛顿法的快速算法

式(17)的优化问题可通过标准内点法进行解算，但运算复杂度较高，为O(N3)． 其中，N为快拍数．考虑到无人机导航实时性要求高，且动态干扰速度快的特点，本研究开发了基于牛顿法的快速算法，来实现对式(17)的高效解算．

对于带有线性约束条件的凸优化问题，牛顿法可为目标函数提供一个下降方向，然后利用一维搜索算法确定搜索步长，获得优化问题的解．这种方法也可扩展到其他下降类算法，如最速下降法等．与最速下降法相比，牛顿法的收敛速度较快，因此本研究只关注牛顿法．

首先，给出式(17)目标函数对于复变量w的导数，即

(18)

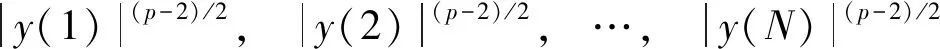
(19)

其中，B为对角矩阵，对角线元素可表示为

(20)

在点w处，式(17)目标函数的二阶泰勒展开为

(21)

式(21)可改写为

(22)

至此，将式(17)转化为新的优化问题，即

(23)

(24)

其中，λ为拉格朗日常数．对式(24)求偏导数可得

(25)

对式(25)中的3个不等式联立，化简后可得

(26)

求解式(26)可得

(27)

(28)

令Hw*w=I, 则式(28)可简化为

(29)

式(17)目标函数下降的方向如式(29)．假定在第k次迭代中的步长为αk， 则下一个点wk+1为

(30)

在每一次迭代过程中，最优步长可由如式(31)这个一维优化问题确定．

(31)

由于p>1时，式(31)中的目标函数对于αk是单模态的，所以，该优化问题可通过线性搜索算法获得．

基于牛顿法的快速算法的时间主要耗费在局部海森矩阵计算上，该算法运算复杂度为O(NM2)， 流程图如图1．

输入:基阵接收数据 X, 最大迭代次数Kmax, 算法收敛门限ε初始化:w0=α(θ0)/α(θ0)22, V^=[α(θ0), Vr]1 for k=0,1,…,Kmax do2 计算y=xHwk, ΔF(wk)=12XC(wk)XHwk,δ^k=-[I-V^(V^HV^)-1V^H]ΔF(wk)3 解算式获得最优步长 αk4 权向量更新为wk+1=wk+αkδ^k5 break if Re(ΔF(wk)δ^k)<ε2 or k>Kmax6 end for7 返回 wopt

图1 基于牛顿法的下降算法流程伪代码

Fig.1 Pseudocode of the framework of descent algorithmbased on Newton’s method

4 仿真分析

通过计算机仿真分析对本研究提出的方法进行验证．假设多天线卫星导航接收机中天线数量为20个，按照均匀线阵排列，天线间距为导航数据载波的半波长，并假设在目标区域存在3颗卫星，方位角θ0=43°、θ1=30°、θ2=75°． 其中，从θ0方位发出的导航信号为期望信号，另外两颗卫星发送的导航信号被视为干扰．同时，在θ3=-60°方位存在一个快速运动的干扰机，其方位角在[-65°，-55°]迅速变化．

4.1 输出波束图

当快拍数为600，SNR=0 dB时，稳健MDDR波束形成器输出波束图随p值的变化如图2．由图2可见，当p取不同值时MDDR波束形成器都可以在43°目标方位形成波束主瓣，在30°和75°方位形成窄的零陷，3颗导航卫星中仅对目标卫星信号增强了．调整主瓣的位置可以对来自不同卫星的导航信号进行接收和增强，从而解算出精确的位置信息．

在预设的[-65°, -55°]区域，MDDR波束形成器输出波束图中形成了一个深度超过-80 dB的凹槽，该凹槽对准高动态干扰方位能够实现对大功率、高动态干扰的有效抑制．相同仿真条件下，文献[7]算法输出波束图如图3．由图3可见，其零陷深度较浅，仅-60 dB左右，且零陷宽度更窄．仿真结果可以说明，本研究提出的MDDR波束形成设计方法在高动态干扰环境中具有良好的稳健性，可提高多天线卫星导航接收机在复杂环境中的性能．

图3 稳健MDDR波束形成与文献[7]输出波束图比较Fig.3 Comparison of the beam patterns of robust MDDR beamforming with Ref.[7]

4.2 输出SINR

当快拍数为600，p取不同值时，稳健MDDR波束形成器输出SINR随输入SNR值的变化情况如图4． 由图4可见：①p值不同时MDDR波束形成器的输出SINR随输入SNR的提高呈上升趋势；② 相同输入SNR情况下，MDDR的输出SINR随p值增大而提高；③ 相同仿真条件下稳健MDDR波束形成器的输出SINR明显高于文献[7]算法，说明本研究提出的波束形成方法在对非高斯信号增强的同时可有效抑制高动态干扰．需要注意的是，p值增大对MDDR波束形成性能影响并不是无限制的．针对同一种次高斯信号，MDDR波束形成器输出的SINR值在p=20.0的结果已经接近p→∞时的结果， 而且p值的增大会令计算量上升．在针对卫星导航信号的MDDR波束形成器设计中，可以在信号增强效果与计算复杂度之间折衷，以便确定p的取值．

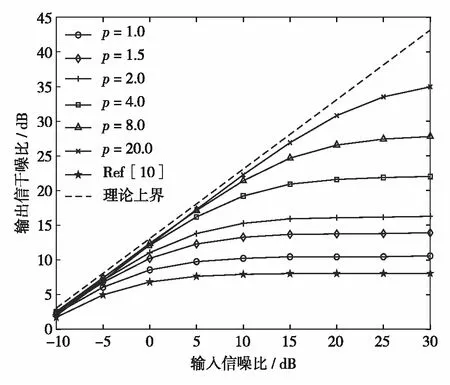
图4 稳健MDDR波束形成器输出SINR随输入SNR的变化情况Fig.4 Comparison of the output SINR versus SNR of robust MDDR beamforming

4.3 算法收敛性

实际工程中，更快的算法收敛速度意味着更少的硬件资源开销和更加简化的导航接收机电路结构．对于功耗、载重及尺寸都有严格限制的无人机，使高效的自适应波束形成算法十分必要．为此，本研究针对稳健MDDR波束形成算法的收敛速度进行计算机仿真研究，仿真实验中设SNR=10 dB，结果如图5．由图5可见，算法的收敛速度随p值的增加而加快，当p=20.0时算法需要400个快拍达到收敛．因此，在面向无人机导航的多天线接收机波束形成算法设计中，可以取p=20.0以获得较快的算法收敛速度．

图5 稳健MDDR输出SINR随快拍数的变化情况Fig.5 Output SINR of robust MDDR beamforming versus the number of snapshots

结 语

受高动态干扰影响，多天线导航接收机收到的卫星导航信号发生畸变，无法为无人机提供可靠的位置信息．针对卫星导航信号非高斯分布的特点，本研究提出了一种基于最小离差准则的稳健波束形成设计方法，提高多天线导航接收机抗动态干扰的稳健性．考虑到无人机导航高实时性的要求，对本文提出的方法开发了快速算法，并通过计算机仿真验证了方法的有效性．另外，本研究提出的稳健波束形成设计方法不受阵列形状的限制，可以应用到线阵、圆阵和面阵等不同形状的天线阵列．