无单元Galerkin方法数值求解三维泊松方程

付 伟，解红霞

(1.太原科技大学 应用科学学院,山西 太原 030024；2.太原学院 应用数学系，山西 太原 030032)

无网格方法是近20年来热门的一种数值计算方法,其中一种方法是无单元Galerkin方法[1-2],简称EFG方法。无网格方法抛开了网格的限制,这是它较有限元算法的优势。

无网格FEM法[3]是Idelsohn等人于2003年提出的,融合了无网格法与FEM法的优点的一类新的数值方法。

2005年,程玉民等[4]提出了复变量MLS法。与较传统的MLS法相比,该方法减少了函数中的变量,有效实现了降维,节约了计算时间,并且有更高的计算精度。

程玉民课题组于2009年提出了二维弹性动力学的复变量边界无单元(CVBEFM)法[5]。与EFG法相结合,先后于2011、2012年提出了针对二维弹性、弹塑性问题的复变量EFG法[6]。MLS法的形函数不具Kronecker δ函数特性,采取措施来施加边界条件就会使Galerkin弱形式更加复杂。

前人用EFG方法数值求解二维泊松方程。本文在此基础上,推导了无单元Galerkin方法数值求解三维泊松方程时的计算公式,改进算法流程,对比解析解和数值解,说明该方法有较好的精度。

1 无单元Galerkin方法

1.1 等效积分弱形式

这里引入一个泊松方程,来探讨无单元Galerkin方法。

Poisson方程:

u(x)-b(x)=0(在Ω内)

(1)

边界条件:

(2)

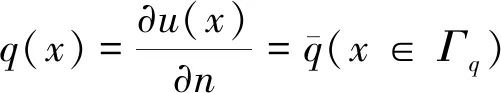
(3)

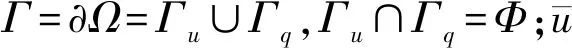
式(1)、式(2)、式(3)的等效积分弱形式为:

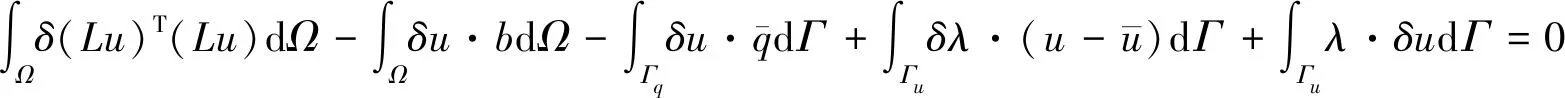
(4)

其中,

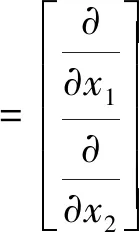
(5)

已知

(6)

其中n是x点区域内的节点个数,Φ(x)函数，

Φ(x)=(φ1(x),φ2(x),…,φn(x))=pTA-1(x)B(x)

(7)

u(x)=(u1,u2,…,un)T=(u(x1),u(x2),…,u(xn))T

(8)

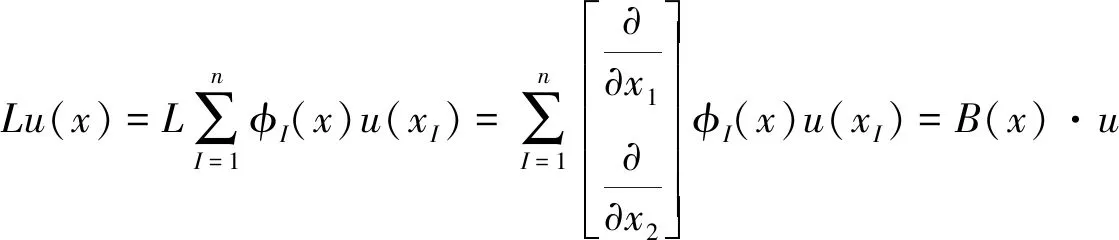
(9)

其中

B(x)=(B1(x),B2(x),…,Bn(x))

(10)

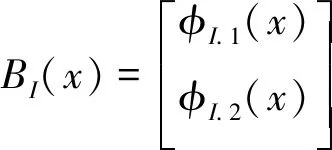
(11)

将(6)和(9)带入(4)得到:

(12)

然后我们对(1.12)的各项进行逐一积分,首先对第一项进行积分:

(13)

其中，

(14)

K=[KIJ]为nt×nt阶的矩阵,

(15)

下面是对(12)第二项进行积分:

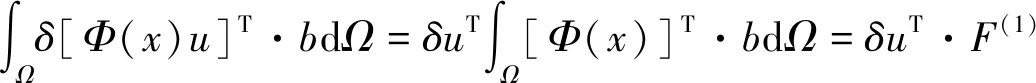
(16)

其中F(1)是给定源函数所引起的荷载列阵

F(1)=(f(1)(x1),f(1)(x2),…,f(1)(xn))T

(17)

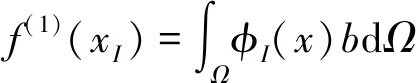
(18)

最后对(12)的第三项进行积分:

(19)

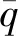
F(2)=(f(2)(x1),f(2)(x2),…,f(2)(xn))T

(20)

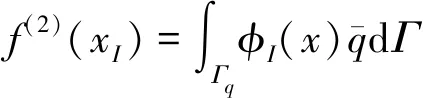
(21)

将式(1.13),(1.16)和(1.19)代入式(1.12)中,得到:

δuT·K·u-δuTF(1)-δuTF(2)=0

(22)

即

δuT·(Ku-F)=0

(23)

其中

F=F(1)+F(2)

(24)

由于δuT的任意性,使我们可以得到线性方程:

Ku=F

(25)

1.2 边界条件的处理

根据式(1)、式(2)和式(3),引入罚因子我们可以得到:

(26)

其中α=(α1,α2,…αi),这里α是罚因子的对角矩阵,针对于二维问题i=2,针对于三维问题时i=3,这个罚因子αk(k=1,2,…i),可能是一个坐标函数,通常情况它是由极大的正数组成。

α=1.0×104～13×max(刚度矩阵K的对象元素)

(27)

[K+Kα]u=F+Fα

(28)

其中

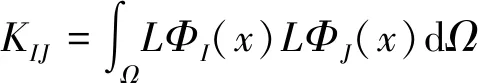
(29)

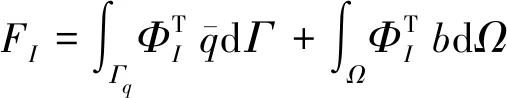
(30)

其中额外的矩阵Kα是由下式(31)所定义的节点矩阵组成的全局惩罚矩阵:

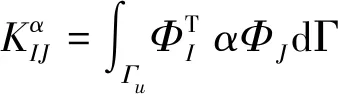
(31)

向量Fα来自于初始边界条件,它的节点矩阵采用下列形式:

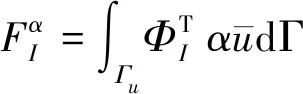
(32)

1.3 背景网格积分方法

定义网格为mi×mi×mi=nN,nN即为节点的总数,对于KIJ、FI转化为如下公式进行积分。

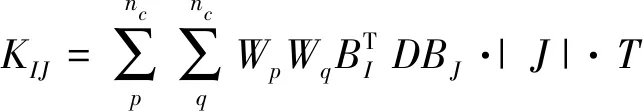
(33)

(34)

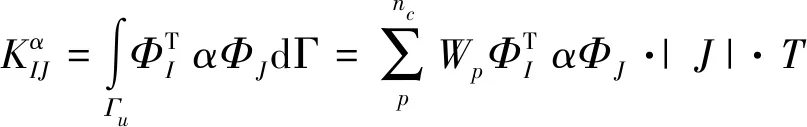
(35)

(36)

1.4 无单元Galerkin方法程序求解流程

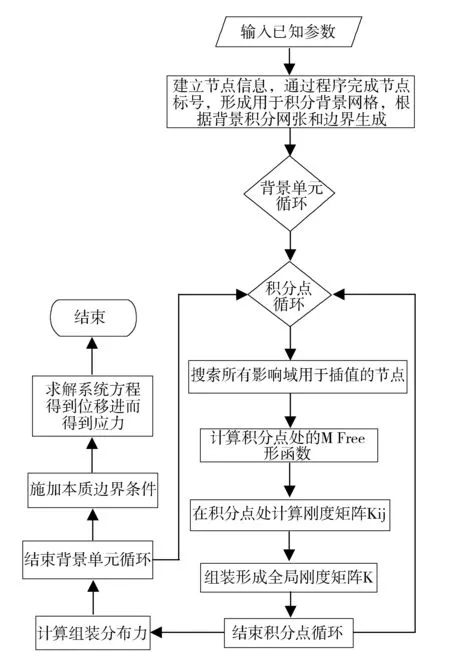
2 无单元Galerkin方法解决三维算例

解决三维泊松方程的数值算例,通过上文中提到的无单元Galerkin方法具体解决一个三维算例。

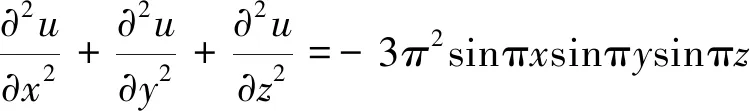
(37)

边界条件为

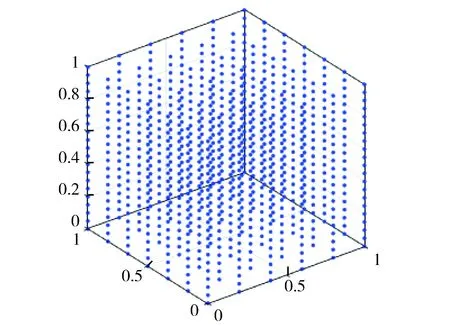
图1 三维数值算例选取节点5×6×20的节点分布Fig.1 Node selection for three-dimensional numerical examples node distribution of 5×6×20

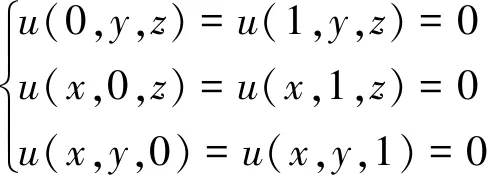
(38)

x∈[0,1],y∈[0,1],z∈[0,1]

(39)

解析解为:

u=sinπxsinπysinπz

(40)

例如对于节点5×6×20，节点分布如图1所示。

通过观察解析解和数值解的误差,得到EFG方法求解三维泊松方程的计算精度。其次,采用不同的节点分布和恰当的dmax,观察对于相对误差值的影响。

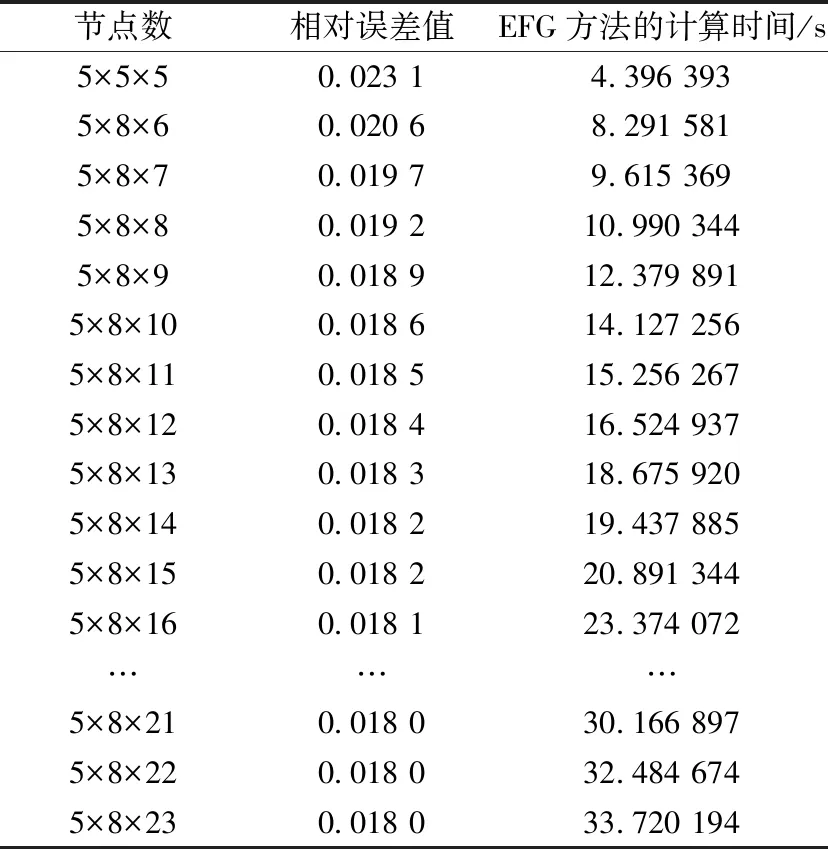
表1 不同布点方式下EFG方法的 相对误差值和所用时间(一)Table 1 The relative error of EFG method and the time used (一)

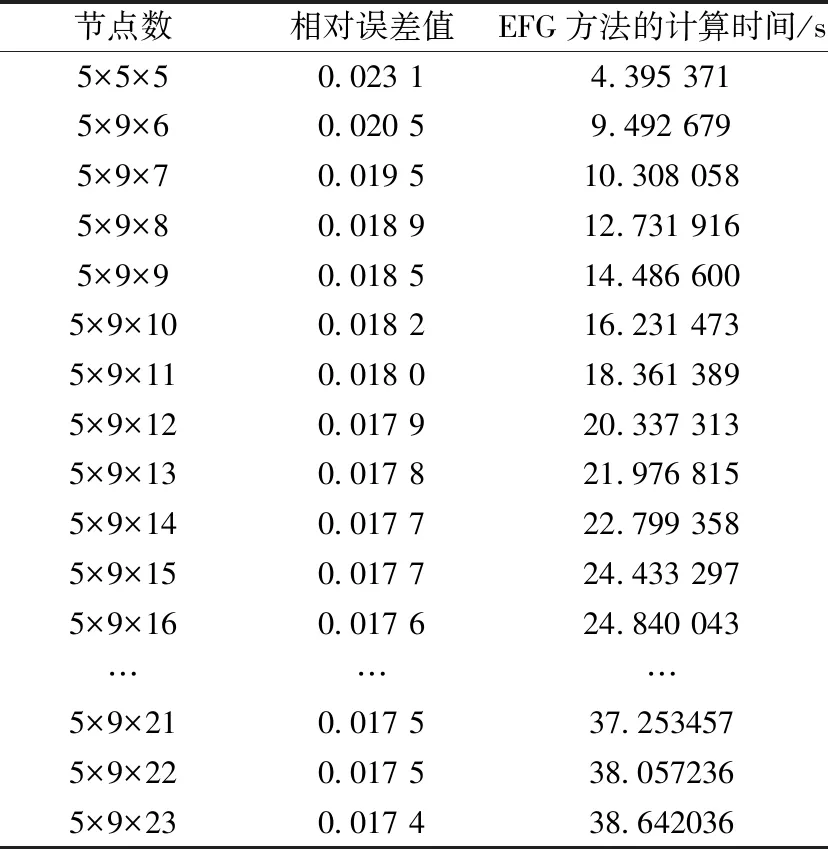
表2 不同布点方式下EFG方法的 相对误差值和所用时间(二)Table 2 The relative error of EFG method and the time used (二)

表1和表2的第一行节点数5×5×5的数据为校准数据,其目的是保证上面两个表的测试条件相同,以免因为内部因素或外部因素的差别而影响误差。从表1的第二行看起,我们是固定x=5,y=8,依次增加z的取值,可以看出随着z的增加,即节点数增多,计算时间也随之增加,误差越来越小,慢慢趋于稳定。单独看表2,从第二行看起同样是固定x和y的值,单纯增加z,与上述结论一致。以表1为比较组,从两个表第二行看起,表2较表1相当于固定了x和z,在对应的同一行中表2中的y等于表1中的y+1,显然表2中的误差更小,同样证明节点数越多,误差越小,拟合效果更佳,但需要的计算时间也更久。

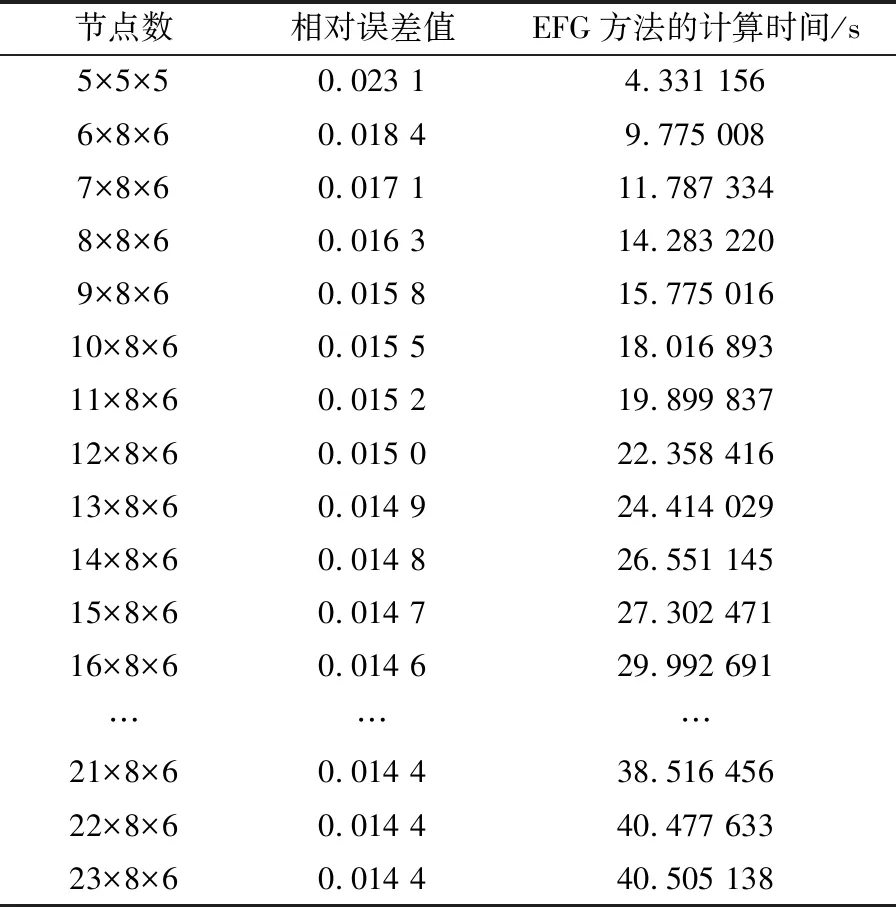
表3 不同布点方式下EFG方法的 相对误差值和所用时间(三)Table 3 The relative error of EFG method and the time used (三)

表4 不同的dmax下EFG方法的 相对误差值和所用时间Table 4 Different dmaxthe relative error value of the EFG method and the time used

为了保证该方法的科学性和有效性,我们首先要做的就是实验的完整性,表3是对于固定y,z,增加x,观察EFG方法所造成的相对误差值和时间。显然随节点数增加误差会减小,计算时间增加,与上述结论一致。综上3个表我们可以看出,随着节点数的增加,误差会逐渐降低。

对于表1、表2和表3是在改变节点数并且固定了dmax=1.22情况下运用EFG的方法,通过观察相对误差和运算时间,首先我们可以看出随着节点数的增加,计算的精确度也随之增加,相对误差值减小,但是同时也增加了计算量,所以所用的时间也增加了。当节点数量增加时基函数的更高完备性阶数实现比低阶有更好的收敛性特征。相反地,从表4可以看出,在节点数不改变的情况,缓慢增加dmax的数值,相对误差值并不是一直减小或增大,最终会围绕着解析解摆动；其中dmax=3.50,是所能测试到的最大值,超过它将无法产生运行结果。

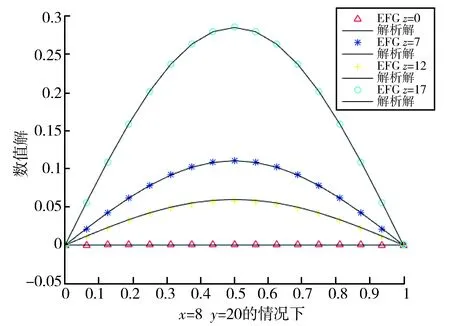
图2 节点数x=8,y=20,dmax=1.60, z取不同值时的曲线拟合图Fig.2 Node number x=8,y=20 dmax=1.60 curve fitting graphs with different value z

下面选择上述测试结果的最优条件,即在x=8,y=20,dmax=1.60,z取不同值的情况下的拟合点和解析解的图像关系如图2所示。

3 结论

从解决三维泊松方程可以看出,对于一个恰当的dmax,当节点数目增加时拟合效果更好。而当节点数保持不变,单独增加dmax的值时,相对误差值并不是一直减小,最终会围绕着解析解摆动。

总之,增加节点数目对于减小相对误差是有效果的,也就是增加节点数目,细化节点单元可达到更好的拟合效果。其次使用EFG方法解决具有特殊边界的三维问题,应当用一个恰当的dmax和较多的节点。