基于有限元分析方法的填充聚四氟乙烯磨损公式拟合

徐时贤 李红波 苏正涛

(1.中国航发北京航空材料研究院 北京 100095；2.中国航空发动机集团减振降噪材料及应用技术重点实验室 北京 100095)

密封根据接触面的形式与状态可以分为静密封和动密封，其中动密封是指密封接触面之间存在相对运动。动密封结构的主要形式有填料密封、橡胶密封圈密封、机械密封、螺旋密封和组合密封等[1]，其中，组合密封的一般组成形式是由聚四氟乙烯(Polytetrafluoroethylene，简称PTFE)密封环和弹性体O形橡胶圈构成。

磨损是决定橡塑密封件使用寿命的关键因素之一。PTFE以其优异的机械性能、耐磨和润滑性能，成为液压传动与控制系统重要的密封件材料[2]。为了获得密封材料的摩擦磨损特性，众多学者开展了摩擦磨损的试验研究[3-6]。这些研究方法主要分为2种：一种是以大量试验为基础研究材料磨损深度的参数化影响，这种研究大多着重于微观层面，研发成本高，且难以和工程实际联系起来；另外一种是在试验结果的基础上，应用有限元仿真方法实现工程实际的预测，而针对这些试验结果在提取数据时，均未考虑实验时试样变形对结果的影响，从而影响了仿真结果的准确性。

本文作者采用环块磨损试验机，开展某种有机材料增强PTFE复合材料的磨损试验，实验原理图如图1所示。实验过程中，实际的磨损区域如图2所示，可以看到试样受挤压后的磨损宽度a为实验的测取值，试样没有环块的挤压作用后，会有一定的弹性回复，磨损形状并不规律，而是在两侧存在具有一定曲率的圆角，圆角两端部的距离即为测量得到的磨损宽度。由于磨损形状无法简单地绘制出来，文中采用平均接触面积来计算接触应力，并引用Rhee的磨损经验公式拟合PTFE材料的磨损经验公式，得到PTFE材料应用时的磨损形状，为后续的密封件设计提供参考。

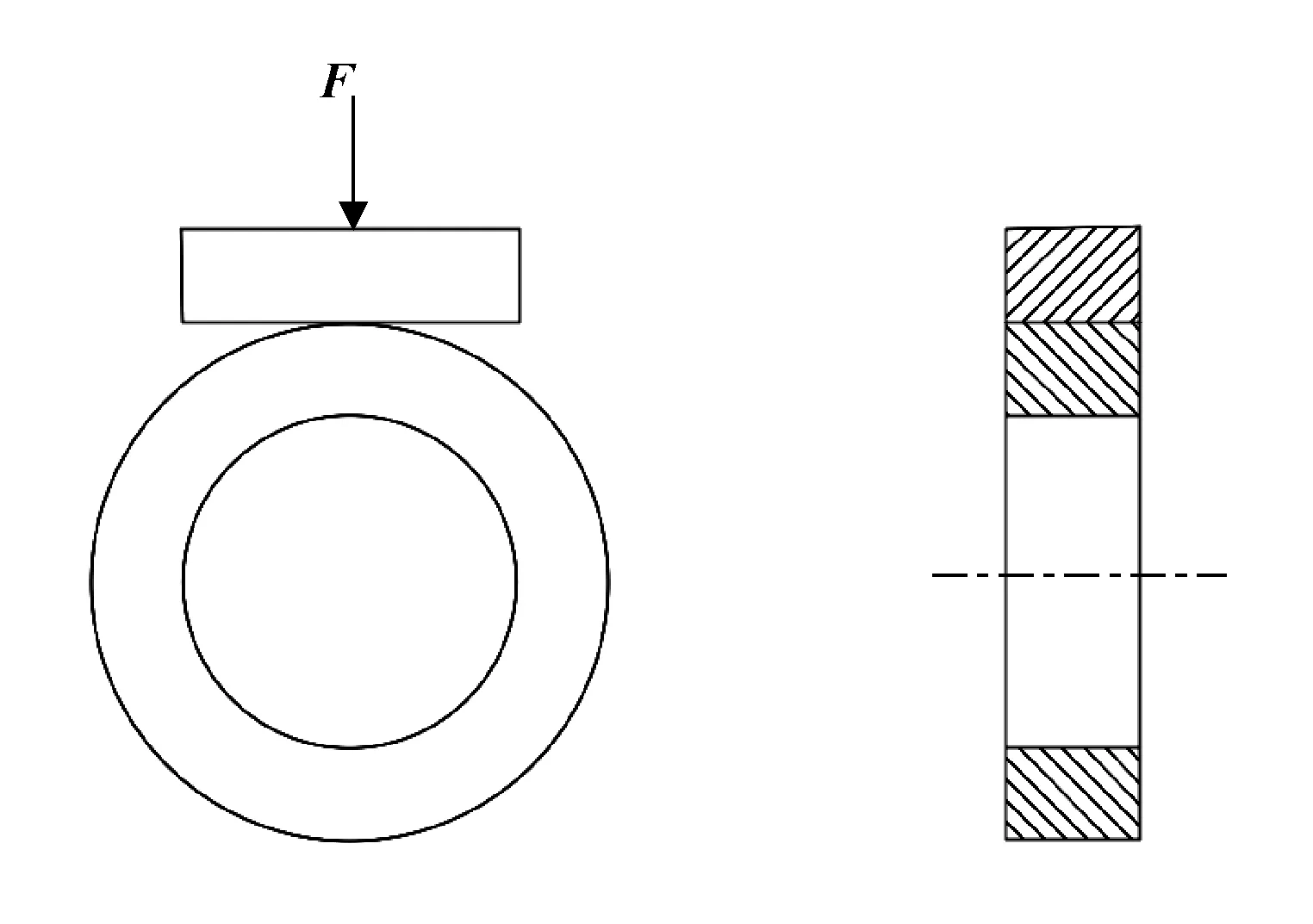
图1 实验原理图

图2 试样受挤压变形原理图

Fig 2 Deformation schematic diagram of specimen subjected to extrusion

1 研究方法

1.1 试验方法

PTFE摩擦磨损试验在MRH-1型高速环块摩擦磨损试验机(如图3所示)上进行，试验材料为往复密封中常用的PTFE材料，其尺寸为6 mm×7 mm×30 mm，对摩环材料为活塞杆常用材料45钢，其外径为40 mm，将其表面粗糙度打磨至0.4 μm。

参照试验方法标准GB/T 3960-2016[7]对试验块进行试验。根据设备所测数据，使所有试验的摩擦因数控制为约0.17。由于磨损量随着压力、速度以及磨损时间等参数的改变而变化，因此分别研究了以上参数单独变化时PTFE材料的磨损情况[8]。试验载荷由砝码的重力提供，分别选择50、100、200、400 N的试验载荷；试验时间选择0.5、1、2、3 h；试验转速选择100、200、300、400 、500 r/min，折合成线速度分别为 0.209、0.419、0.628、0.837、1.047 m/s。

图3 MRH-1型高速环块摩擦磨损试验机

1.2 磨损模型计算

根据RHEE[9]的研究，磨损量服从下式：

ΔW=kpavbtc

(1)

式中：ΔW为磨损质量(mg)；k、a、b、c为公式的拟合系数；p为磨损区域的接触应力(MPa)；v为磨损速度(m/s)；t为磨损时间(h)。

通过提取磨损试验中的系数拟合公式(1)所示的磨损公式，然后根据该公式将有限元模型文件中的节点坐标进行调节，模型文件按照图4所示步骤进行调节[10-11]，可以得到一定转速、压力和时间下的试验件磨损情况，整个计算的执行采取Python语言进行编辑。Python语言程序可以读取Abaqus软件odb结果中的节点坐标和接触应力值，计算时，可以选一定量为坐标的调整值，其与磨损公式计算出来的最大位移相比，就可以得到坐标调整的加速系数，所有相关节点的调整量可以通过加速得到。当所有加速系数之和比总循环次数大时，循环结束，可以得到最终计算结果。

循环过程中，为了防止出现单元畸变的情况，在环块模型中除了在与轴接触的部分设置第一层节点外，在模型厚度方向上分别设置多层节点，这些节点的坐标可以随着第一层节点的坐标均匀变化，这样可以有效防止节点坐标变化导致的单元畸变。

图4 模型调整步骤

2 数据拟合

2.1 磨损宽度测量

将不同工况下的试样的磨损宽度记录下来，如表1所示。

表1 PTFE磨损试验数据

2.2 数据提取

由于试验后磨损量不易称量，根据下式对磨损体积进行计算：

(2)

式中:V为磨损体积(mm3);bs为试样宽度(mm);R为磨损环块的外径(mm)。

根据弧长公式，可以得到磨损后的PTFE接触区域的面积：

(3)

式中:S为接触区域的面积(mm2)。

建立磨损试验的有限元模型，如图5所示，通过如图6所示的结果可以发现，磨损区域的接触应力在中部是比较集中的，而磨损的过程类似于刀具的切削过程，接触区域的切削量是匀速等量的，这就可以假设在磨损过程中接触区域的接触应力是均匀分布的，其不受压力大小的影响。

接触应力和接触区域在磨损前后是不相同的，且在磨损过程中一直变化，文中忽略试样厚度方向的变化，通过公式(2)计算得到磨损体积，通过公式(3)计算磨损后试样的接触面积。按照理想化的接触情况来看，在未磨损时接触面积应该为0；随着磨损宽度的增加，接触面积逐渐增大，而用于计算磨损公式的接触应力值是一个平均值，而不是磨损后的最终值。因此，文中求得平均接触面积(如表2所示)，并根据此值求解平均接触应力值，作为公式(1)的输入参数。

图5 磨损实验有限元模型

图6 磨损试样的接触应力分布图

试样号磨损后接触面积S/mm2平均接触面积Sa/mm2磨损量ΔW/mg126.8813.444.43231.8915.957.40333.5916.798.64434.4417.229.31514.597.290.71619.289.641.64741.2420.6215.97827.2413.624.61928.3914.195.221028.6314.315.361129.7214.865.991230.0215.016.171330.3215.166.36

2.3 数据处理

将不同工况下的计算结果折算成磨损公式所需的p、v、t值，如表3所示，并将这些值与磨损深度相对应，使用origin软件进行拟合，可以得到：k=0.007 54，a=2.792 38，b=0.989 33，c=0.357 29。将不同工况下的结果绘制于图7中，可以发现曲线拟合效果良好，由于对于不同的压力，得到p值并不相等，因此采用图7(b)和图7(c)所示的三坐标图来表征不同p与v和不同p与t的结果。

表3 PTFE实验数据处理

图7 公式拟合结果对比

Fig 7 Formula fitting results comparison (a)relationship between pressure and wear volume; (b)the relationship between pressure,speed and wear volume; (c)the relationship between pressure,time and wear volume

3 结果对比

根据磨损公式对有限元模型进行调整，如图8所示，图8(a)所示为转速300 r/min，压力200 N、时间2 h后有限元计算的输入模型，将其进行计算，可以得到如图8(b)所示的接触应力云图，可以看出，接触应力分布比较均匀。将计算结果与试验结果进行对比，如表4所示，可以发现两者吻合良好，而计算精度与网格尺寸有关，即在计算能力允许范围内，通过细化网格可以降低计算误差。

图8 磨损有限元仿真结果

试样号磨损宽度b/mm实验结果计算结果计算误差e/%25.35.41.8952.432.41.2384.534.50.694.724.81.69

4 结论

通过环块磨损试验，定量研究了有机填充PTFE复合材料的磨损规律。在拟合磨损公式时，采用平均接触面积的方法估算接触应力，将拟合出来的磨损公式，利用Python语言循环调整模型的输入文件，计算结果与实验结果吻合良好，一方面说明，这种估算接触应力的计算方法可以准确地用于磨损的有限元计算，另一方面说明，基于磨损公式进行的节点调整方法是相对准确的，这种输入文件的编辑方法可以为密封件的产品设计和寿命预测提供参考。