大型轴流泵泥沙磨损特性研究*

林 鹏1 刘和云1 胡 东1 刘梅清 王 舒1 赵文胜

(1.湖南人文科技学院能源与机电工程学院 湖南娄底 417000；2.武汉大学动力与机械学院 湖北武汉 430072)

大型轴流泵用于泥沙含量高、悬浮颗粒和杂质多的场合时，叶片易磨损、缠绕，严重时会烧毁水泵电机[1]。一般而言，叶轮是水泵部件中最容易被严重磨损的部件之一，尤其是因磨损而使叶片失效[2-3]。

预测磨损率的磨损模型，一般均认为局部的磨损率主要是颗粒速度和入射角的函数[4-6]。HUMPHREY[4]认为磨蚀率与颗粒入射角有关；TABAKOFF等[7]提出了多参数磨损经验方程，包含颗粒碰撞速度和角度等参数；IWAIT和NAMBU[8]研究了13种常用水泵材料在不同射流速度、冲击角度、泥沙粒径和浓度条件下的磨损特性，认为超过临界射流速度和一定泥沙浓度后，磨损率将急剧増大；梁武科等[9]分析了不锈钢、碳钢、堆焊焊条及合金粉末喷焊材料抗磨蚀特性与含沙量、流速的关系，发现含沙量和流速均促进了材料的磨损破坏作用。

在泥沙磨损方面，张自超[10]采用改进的固液两相流欧拉算法，考虑了相间阻力和泥沙扩散系数两方面因素，对典型悬移质泥沙粒径条件下的双吸离心泵流场进行了数值计算，发现叶片表面湍流强度在头部和尾部较大；黄先北等[11]基于Particle模型和Tabakoff 磨损模型，获得了不同泥沙和入口条件下单吸泵内颗粒运动轨迹和磨损规律；施卫东等[12]对潜水轴流泵的固液两相流动特性进行研究，认为固相浓度高的部位磨损严重；李文锋等[13]采用Particle模型和颗粒单向耦合模型，对离心泵抽送不同直径的泥沙颗粒的混合液进行了数值模拟，发现颗粒的分布与流道的布置方式、颗粒的大小均有重要关系，泵内部磨损与固体颗粒的相对速度、浓度、颗粒大小也有直接关系；YANG等[14]采用欧拉-拉格朗日方法对双吸离心泵进行磨损研究，得到颗粒粒径和含沙浓度的增加，叶片磨损率増大的结论；林鹏等人[15]采用Particle模型和非均相流模型定性分析了轴流泵内固液两相的分布情况及磨损特性。

以上研究均是对过流部件进行定性分析，未能进行定量研究。故本文作者对轴流泵过流部件的磨损进行定量研究，进而得到泥沙在轴流泵内部的流动规律及磨损机制。

1 轴流泵模型

1.1 设计参数

轴流泵装配总图，如图1所示，其设计参数见表1所示。

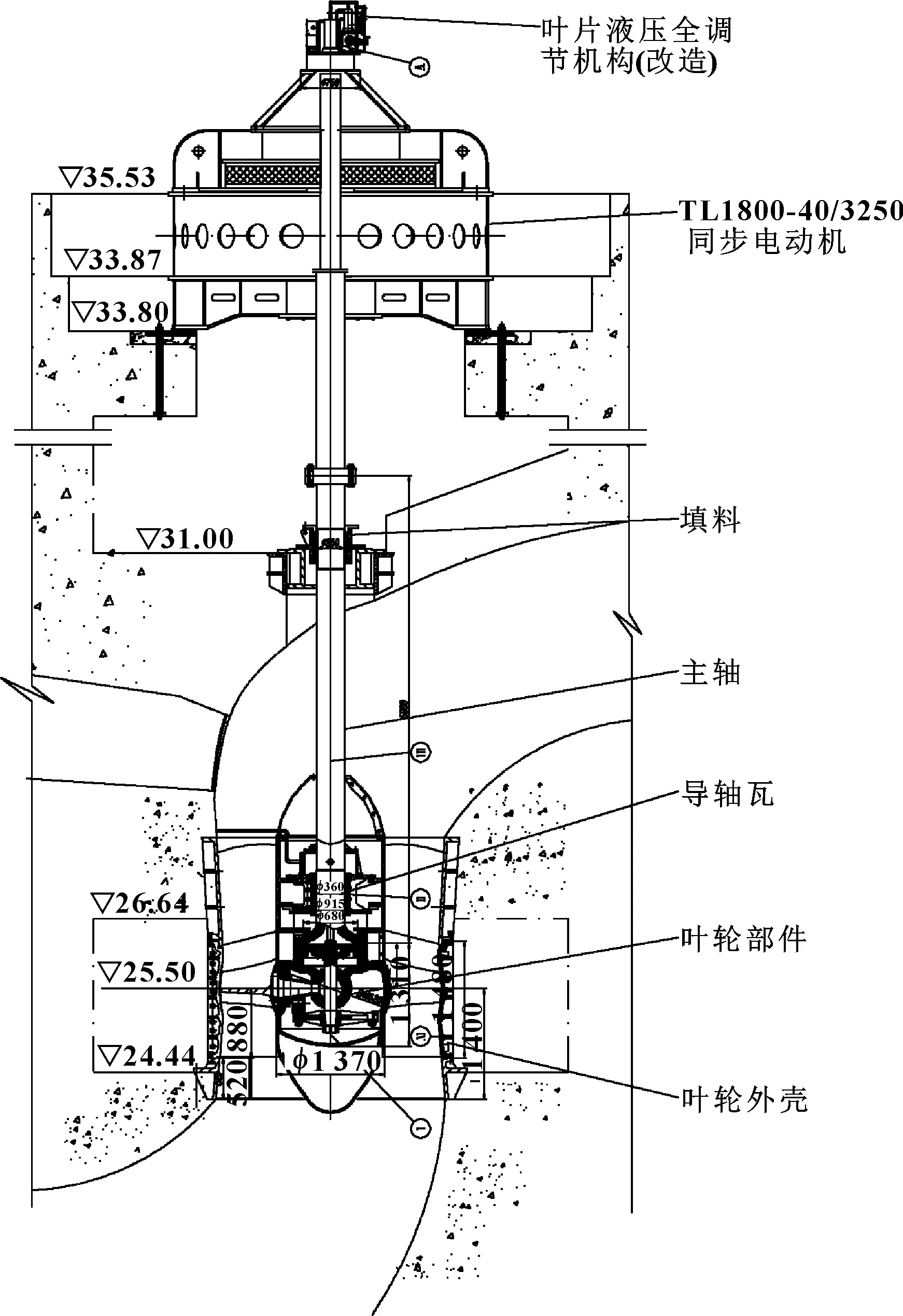
图1 大型立式轴流泵装配总图

型号扬程H/m流量Q/(m3·s-1)额定转速n/(r·min-1)额定效率η/%比转速ns28CJ-705.3021.2515088.6788

1.2 轴流泵计算域及网格划分

为了与大型轴流泵的出厂测试(泵段试验)相对应，简化了大型轴流泵进、出口流道，计算域如图2(a)所示，整体网格划分如图2(b)所示。

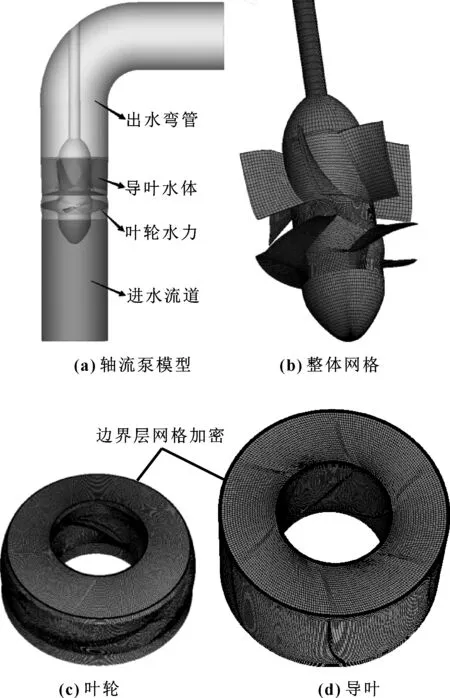
图2 轴流泵模型和结构网格划分

1.3 网格无关性验证

由边界层网格要求，需对叶轮和导叶边界层网格加密，以保证壁面y+≈1，如图2(c)、(d)所示。

网格无关性分析结果如表2所示。考虑计算误差和计算效率，最终选用方案2的网格进行相关后续研究。

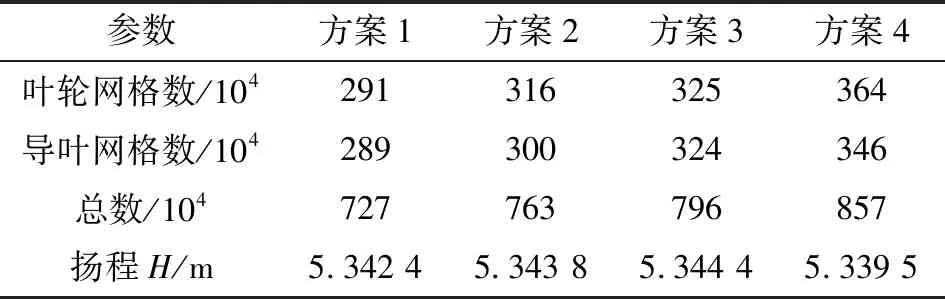
表2 网格无关性分析

1.4 数值计算方法及基本假设

进行数值模拟时，采用非均相流模型，对于连续相，采用SSTk-ω湍流模型；离散相采用零方程模型[16]。考虑滑移速度和相间拖拽力的影响，拽力系数采用Schiller Naumann 模型[17]，表达式为

(1)

式中：CD为拽力系数；Re为液相雷诺数，量纲为一。

2 磨损模型和磨损率

2.1 磨损模型

采用Tabakoff 磨损模型进行磨损计算。预测磨损所用的Tabakoff 磨损模型是基于颗粒轨迹来进行计算的，是TABAKOFF和GRANT[18]研究不同颗粒射流速度和入射角度对靶材磨损的影响下得出的经验与半经验磨损模型。

2.2 磨损率

颗粒的碰撞速度与角度、颗粒本身的属性、材料表面的属性都影响到带粒流磨损量，即在单位时间内，颗粒作用于单位面积材料表面所切削掉的材料质量，也叫磨损率，其计算公式为

(2)

其中：

(3)

(4)

式中：E为表面磨损率，量纲为一；θ为粒子碰撞角度，( °)；vP为粒子冲击速度，m/s；v1、v2、v3为粒子碰撞速度参数，m/s；k1、k12、θ0为常数；θ0为最大磨损率所对应的入射角度，( °)。

式(2)可分为两部分：第1部分为颗粒小角度切削损伤，即为颗粒对展性材料的破坏机制；第2部分为颗粒法向速度对靶材的侵蚀损伤，正比于速度的4次方，即为颗粒对脆性材料的破坏机制。

表3 模型参数

因为该磨损模型兼顾了展性和脆性材料的共同影响，所以能较为全面地预测磨损特征。目前该磨损模型主要适用于钢制、铝制等材料，具体参数如表3所示，文中选用钢制材料进行研究。入射方式选择均匀分布，指定粒子数量为20 000个。

3 外特性验证

3.1 清水外特性

分别选用Standardk-ε，RNGk-ε，SSTk-ω和Standardk-ω湍流模型进行数值计算，得到轴流泵的外特性曲线，与真机试验进行对比，为大型轴流泵找寻最为合适的湍流模型。

定义流量系数δQ=Q/Q设(Q为任意时刻的流量，Q设为泵的设计流量)，图3所示为不同湍流模型时轴流泵流量系数δQ-H曲线。

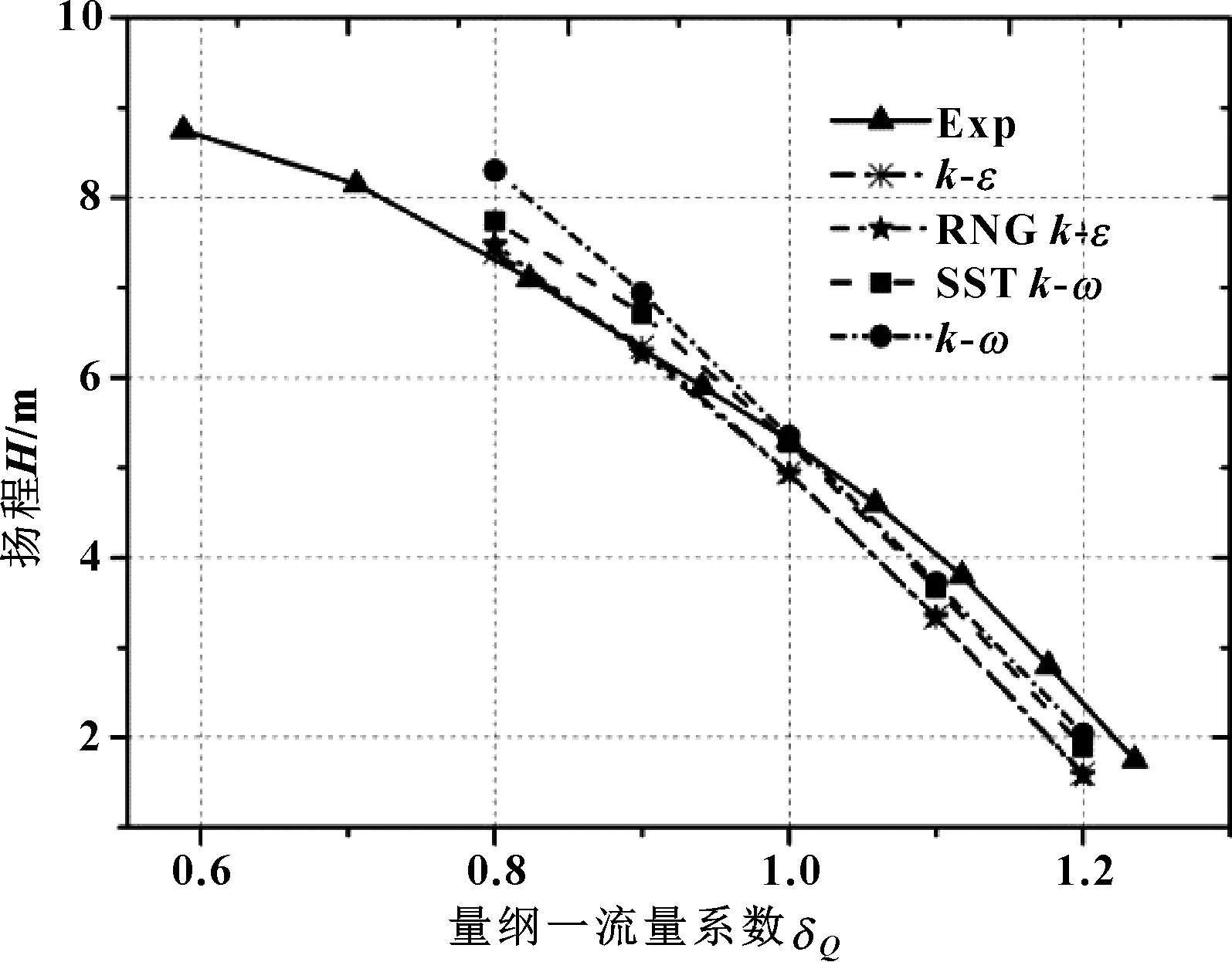
图3 不同湍流模型轴流泵流量-扬程曲线

从图3中可以看到，在小流量工况时，Standardk-ε，RNGk-ε湍流模型与试验值接近，而大流量工况则与试验值偏差较大；Standardk-ω湍流模型在设计工况时，与试验值吻合较好，偏离设计工况，则误差较大；SSTk-ω湍流模型则兼具其他3种湍流模型的优点，与试验值匹配最好。

图4所示为不同湍流模型时轴流泵流量系数δQ-η曲线，可知，效率曲线与扬程曲线的规律相似，SSTk-ω湍流模型的效率值同样与试验值匹配最好。因此，后续的数值模拟均选取SSTk-ω湍流模型进行计算。

图4 不同湍流模型轴流泵流量-效率曲线

3.2 含沙水外特性

图5所示为轴流泵分别抽送粒径d=0.5 mm、含沙量Vm=5%体积分数的含沙水和清水时的外特性计算值与清水试验值的对比。

图5 试验性能与预测性能对比

由图5可知，外特性计算值与试验值具有良好的一致性，说明SSTk-ω湍流模型在轴流泵输送清水和含沙水的数值计算中具有很好的适用性。轴流泵输送含有杂质的水流时，其扬程和效率均略有下降，小流量时的降幅大于其他工况。

4 泵内磨损特性分析

研究泥沙粒径(d)、含沙量(Vm)对颗粒运动轨迹和叶轮磨损率的影响，具体计算方案如表4所示。

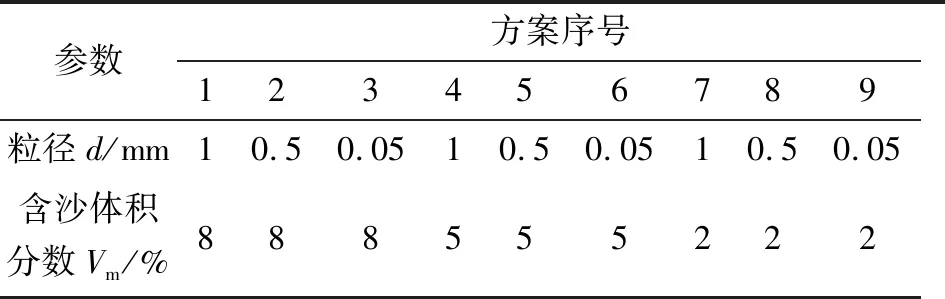
表4 计算方案

4.1 粒径对沙粒运动轨迹的影响

图6所示为含沙体积分数Vm=5%时，不同泥沙粒径的单个颗粒运动轨迹。

可知，单个泥沙的运动速度随粒径的增大而增大，最小速度由2.11 m/s增大为3.22 m/s，最大速度由13.23 m/s增大为13.54 m/s；在图中圆圈内，可以看到，随着粒径的增大，泥沙颗粒向叶片工作面运动的趋势更为明显。

图7所示为多个不同粒径泥沙颗粒在流道内的运动轨迹。可看出，在叶轮和导叶内部，泥沙颗粒的分布规律相似。在叶轮内直径较大的泥沙颗粒主要分布在叶片工作面外缘(见图7(b))，粒子直径越大，越位于叶轮外缘处，说明大直径泥沙主要受叶轮离心力的影响；直径较小的泥沙颗粒，主要分散在流道中部(见图7(a))，说明小直径泥沙受叶轮离心力的影响不大，与水流的流动性较好；在导叶内部，大直径泥沙主要分布在导叶的轮缘处，较小直径的泥沙颗粒更多分布在导叶轮毂附近及中间流道内，说明导叶内泥沙颗粒主要受其自身惯性力的影响。

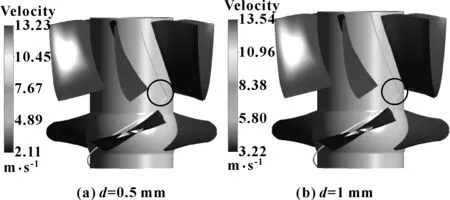
图6 不同粒径下单个颗粒运动轨迹(Vm=5%)

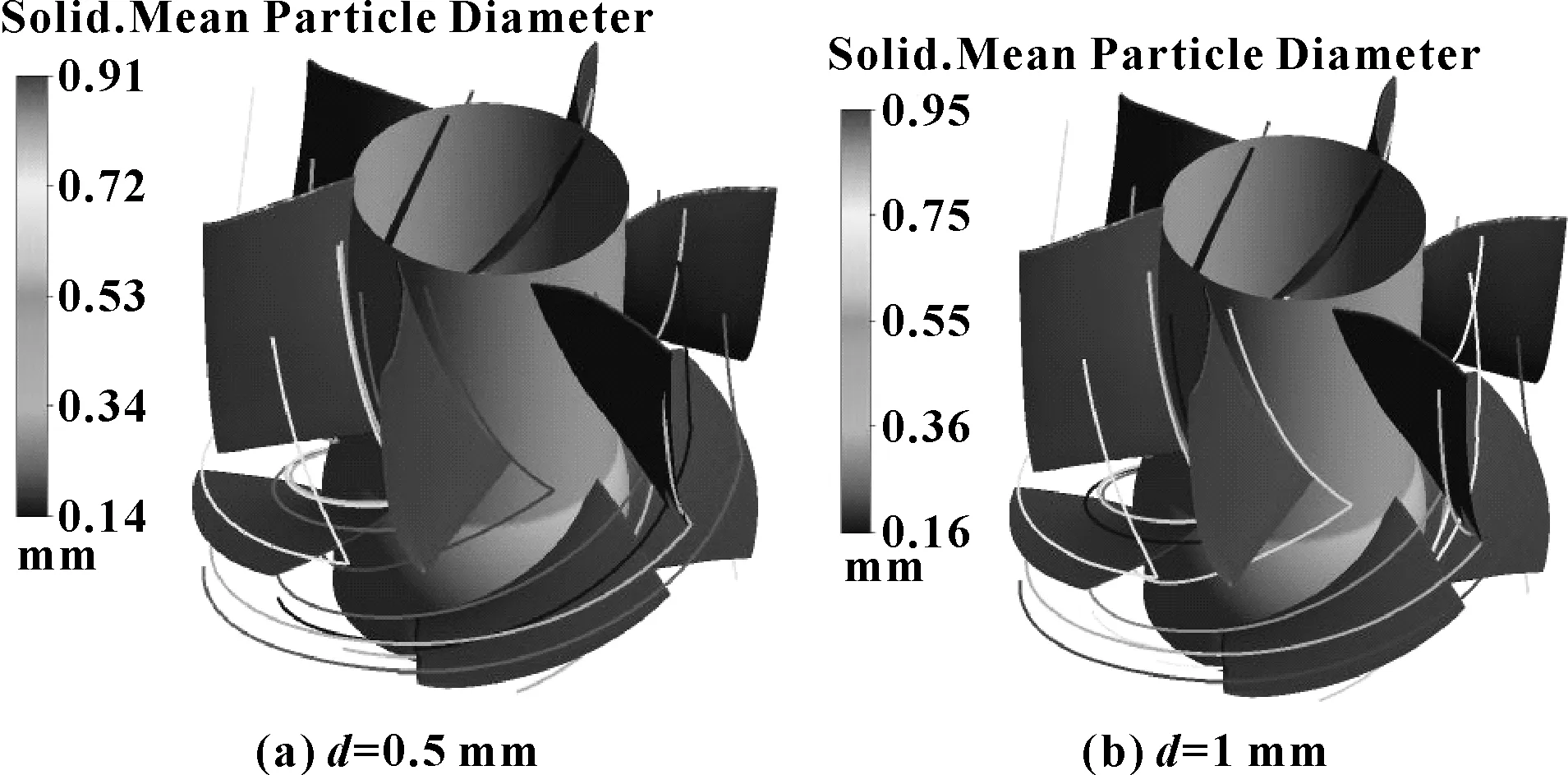
图7 不同粒径下多个颗粒轨道分布(Vm=5%)

文献[19]的试验研究表明，大直径泥沙易向叶片工作面移动，易与叶片头部发生碰撞；小直径泥沙易与叶片工作面后端发生碰撞，这与文中计算结果一致。

4.2 含沙量对沙粒运动轨迹的影响

图8为泥沙粒径d=0.5 mm，入口含沙体积分数Vm=5%和Vm=8%时，泵内部单个沙粒的运动轨迹。可以看出图8(a)和图8(b)几乎一样，说明泥沙颗粒运动轨迹受到含沙量的影响不大。这是由于泥沙颗粒的受力状态与粒径有关，与含沙量无关，因此，无论含沙量多少，其运动轨迹均不发生改变，故不再列出多个颗粒的运动轨迹。

图8 不同含沙量下单个颗粒运动轨迹(d=0.5 mm)

4.3 粒径对过流部件磨损的影响

图9、10所示为沙粒入口含沙体积分数Vm=5%时，不同泥沙粒径下的叶轮叶片表面磨损率密度(简称磨损率)。可知，叶片进口边磨损率最大，此处磨损最严重；随着泥沙粒径的增大，磨损率范围增大，磨损强度也相应增大。工作面磨损范围由叶片进口边逐渐向叶片出口边外缘方向移动，叶片背面基本全部集中于进口边，磨损范围基本不变。

图9 叶片表面磨损率分布(d=0.5 mm，Vm=5%)

图10 叶片表面磨损率分布(d=1 mm，Vm=5%)

图11所示为沙粒入口含沙体积分数Vm=5%时，不同泥沙粒径下的叶轮叶片表面不同位置处磨损率分布曲线。可知，沿叶轮进口到出口方向，轮毂和轮缘处的磨损率几乎为0；中间截面处大颗粒磨损率明显大于小颗粒磨损率，即泥沙对过流部件壁面的磨损速度与颗粒粒径成正比，与实际情况相符。

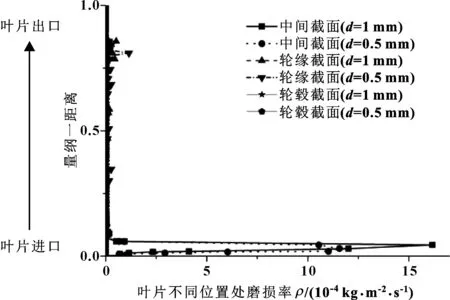
图11 叶片表面不同位置处磨损率分布曲线(Vm=5%)

4.4 含沙量对过流部件磨损的影响

图12所示为粒径d=0.5 mm时，叶片表面不同流线处磨损率随颗粒含沙量的变化曲线。

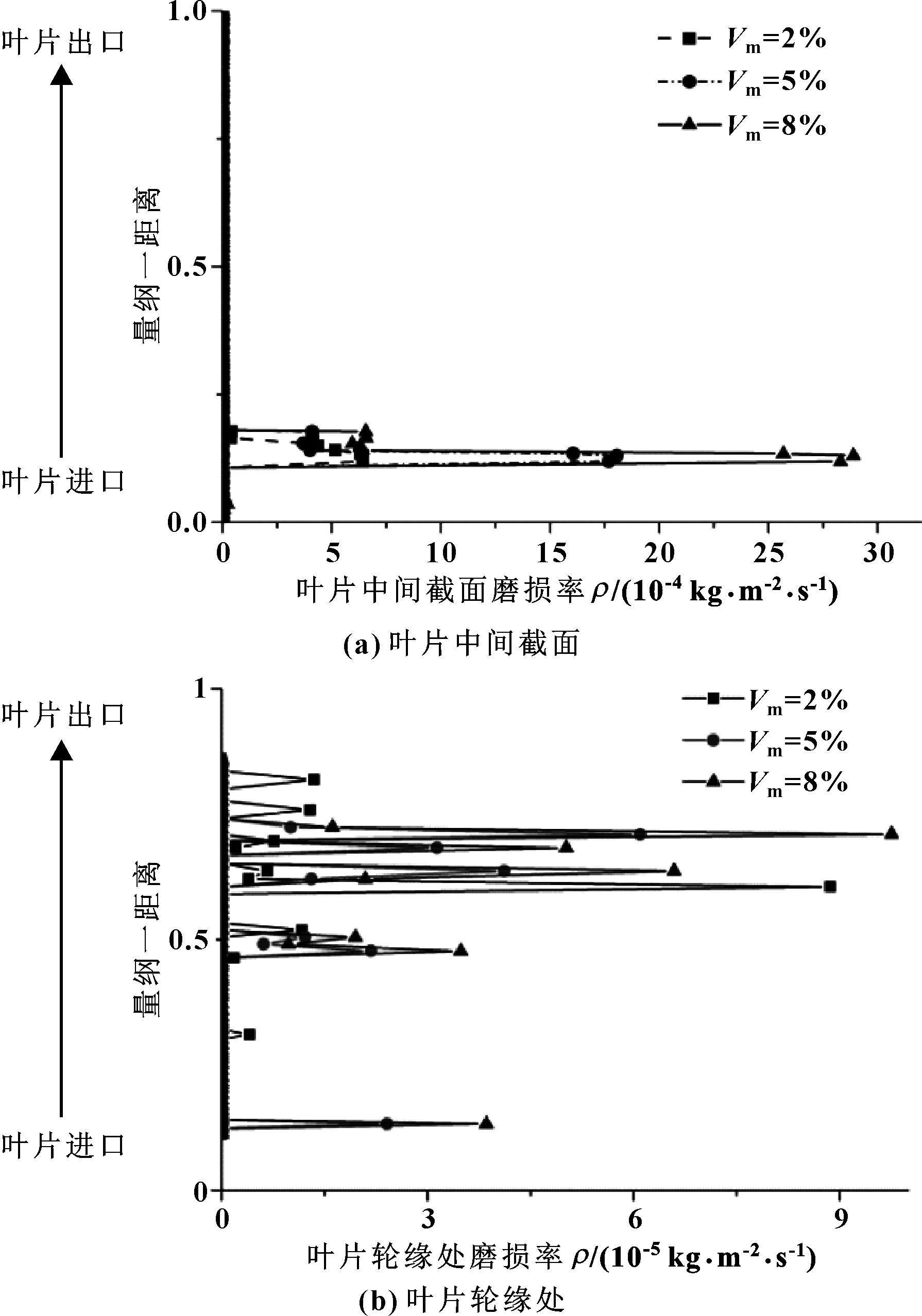
图12 叶片不同流线处磨损率随含沙量变化曲线(d=0.5 mm)

可知，在叶轮内，磨损率主要分布在叶片进口及叶轮流道内，轮毂处为0，轮缘处磨损率非常低，几乎为0；粒径不变时，随着含沙量的增大，叶轮内各处磨损率均增大。由此可知，磨损率受到颗粒含沙量的影响显著，说明颗粒含沙量是影响磨损率的主要因素之一。

4.5 含沙量和粒径对最大磨损率的影响

图13所示为最大磨损率随含沙量和直径的变化曲线。可知，最大磨损率与含沙量和粒径成正比，在同一粒径下，随着含沙量的增大，最大磨损率几乎成线性增长，然而，粒径越大，最大磨损率的增幅也越大。

图13 不同粒径和含沙量时叶片最大磨损率分布曲线

在同一含沙量下，随着粒径的增大，最大磨损率也随之增大，然而，最大磨损率随粒径增大的幅度不一样。

当含沙量较小(Vm=2%)时，随着粒径的增大，最大磨损率增幅较小；当含沙量继续增大(Vm=5%、8%)时，随着粒径的增大，最大磨损率增幅越大。说明含沙量和粒径均是加快叶轮磨损的重要因素，与前文现象描述一致。

5 结论

(1)外特性计算值与试验值具有良好的一致性，说明SSTk-ω湍流模型在轴流泵输送清水和含沙水的数值计算中具有很好的适用性。泵输送含有杂质的水流时，其扬程和效率均略有下降，小流量时的降幅大于其他工况。

(2)叶片头部及叶片工作面的泥沙体积分数和磨损率最大，导致叶片头部、工作面磨损速度和程度大于背面。

(3)粒径对泥沙的运动轨迹有显著影响，而含沙量的改变对泥沙的运动轨迹影响不大；颗粒在叶轮中的运动速度与粒径呈正相关关系，粒径大的沙粒向叶片工作面运动的趋势更为明显，说明粒径为影响泥沙运动轨迹的一个主要因素，含沙量为一个次要因素。

(4)随着粒径的增大，磨损率范围增大，磨损强度也相应增大。工作面磨损范围由叶片进口边逐渐向叶片出口边外缘方向移动，叶片背面基本全部集中于进口边，磨损范围基本不变。随着含沙量的增大，叶轮内各处磨损率均增大。

(5)最大磨损率与含沙量和粒径成正比，在同一粒径下，随着含沙量的增大，最大磨损率几乎成线性增长，说明含沙量和粒径均为影响磨损率的重要因素。