双稳态压电振动能量采集器的时-频域动力学特性及实验研究*

赵泽翔,王光庆,谭江平,崔素娟,武海强

(浙江工商大学信息与电子工程学院,杭州 310018)

双稳态压电振动能量采集器是一种将环境中振动能采集并转化成电能的非线性机电耦合器件,具有工作频带宽、转换效率高等优点,在无线传感器网络节点和微电子设备的供电系统中具有良好的应用前景[1-6]。

国、内外对双稳态压电振动能量采集器进行了大量研究,并取得了较丰富的研究成果。Minghui Y A[7]等人提出了双稳态L形梁结构,理论分析得到该系统的势能函数具有两个对称的稳定势阱。此外,当考虑重力势能时,势能函数则出现不对称的双势阱。李海涛[8]等人利用Melnikov方法建立了双稳态压电模型并分析了系统的同宿分岔和混沌等非线性动力学行为,研究结果表明Melnikov方法可为能量采集器的参数设计提供有效的理论依据。Sovan Sundar Dasgupta[9]等人利用Fokker-Planck-Kolmogorov方程,研究了高斯白噪声激发的非线性双稳态能量采集器的系统参数对振荡器的位移和速度的概率分布以及输出电压的均方的影响,结果表明振荡器的位移和速度的联合概率分布的最大峰值随着噪声强度值的增大减小。

尽管如此,双稳态压电振动能量采集器还有很多科学问题需要深入研究,如双稳态压电振动能量采集器的时-频域动力学响应特性对系统参数的敏感性问题,它是优化双稳态压电振动能量采集器结构以及提升其综合输出性能的关键因素。目前,针对双稳态压电振动能量采集器动力学响应特性的研究要么侧重于从时域角度去分析系统参数对其动力学特性的影响,要么侧重于从频域角度分析双稳态压电振动能量采集器在系统参数作用下的频率响应特性。这些都不能全面揭示双稳态压电振动能量采集器的非线性振动激励和动力学响应特性,以至于无法对双稳态压电振动能量采集器进行结构优化参数设计和综合性能提高。本文分别从时域和频域两个角度综合研究分析系统参数对双稳态压电振动能量采集器动力学响应特性的影响,为揭示双稳态压电振动能量采集器的动力学特性和非线性作用机制提供全方位的视角。本文考虑振型和分布参数对输出性能的影响,利用拉格朗日方程和Raleigh-Ritz方法建立了双稳态压电悬臂梁振动能量采集器分布参数非线性机电耦合动力学模型,并利用龙格库塔算法(ODE45)对双稳态压电悬臂梁振动能量采集器进行仿真,研究激振加速度、磁铁对间距、激振频率对系统动力学特性的影响;此外,利用谐波平衡法对双稳态压电悬臂梁振动能量采集器进行频域分析,研究激振加速度、磁铁对间距、激振频率、负载阻抗对系统采集输出电特性(电压、电功率)的影响,比较了不同激励频率、磁铁对间距对最优阻抗的影响,并利用实验进行验证。

1 双稳态压电振动能量采集器建模

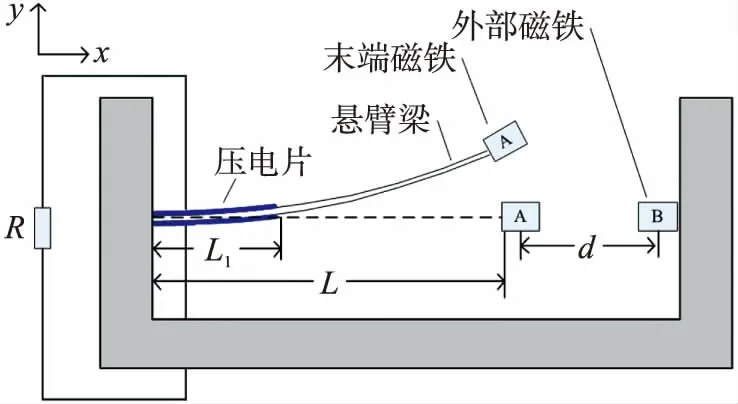
图1 双稳态压电振动能量采集器结构示意图

考虑图1所示的双稳态压电振动能量采集器结构为主要研究对象,它主要由压电双晶片悬臂梁和两个磁铁A、B构成。两片长度均为L1且极化方向相反的压电片对称粘结在长度为L的悬臂梁根部上、下表面,压电片串联连接负载电阻R;压电双晶悬臂梁一端固定在基座左侧,另一端连接磁铁A(简称末端磁铁);外部磁铁B粘结在基座右侧,并与末端磁铁A水平相距为d。

1.1 非线性磁力模型

图1所示压电双晶悬臂梁末端磁铁A受到磁铁B的非线性排斥力可以通过点磁荷模型计算得到,如图2所示为磁铁A与磁铁B之间的几何关系,图中L为悬臂梁长度,a为磁铁长度的一半,w(x,t)为悬臂梁x处的振动位移,α=∂w(L,t)/∂x为磁铁A的偏转角,这里假设磁铁的偏转角很小。同时,假设磁铁A、B中磁场分布是均匀的,且磁极本身的几何线度远小于磁铁间的距离,则磁铁A、B可以看成是点磁荷,采用磁偶极子模型计算得到磁铁B和磁铁A之间的势能为[9-10]

(1)

式中:μ0=4π×10-7H/m为真空磁导率,为向量梯度,mA为偶极子A的磁矩,mB为偶极子B的磁矩,且mB=MBVB,MB为磁铁B的磁化强度,VB为磁铁B的体积,rBA为磁铁B到磁铁A的方向向量。

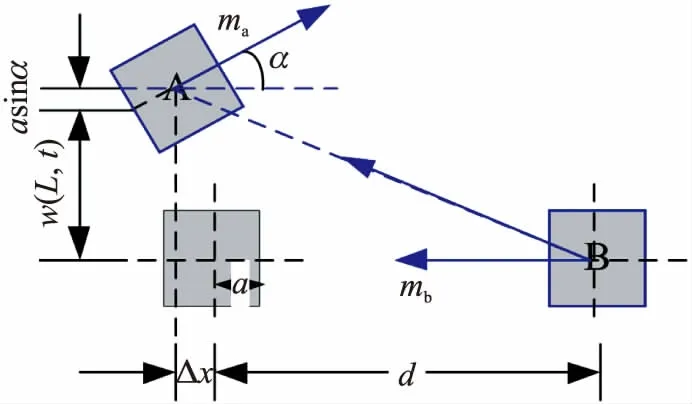
图2 非线性磁力模型

由图2可以得到:

rBA=-d·i+w(L,t)·j+0.k
mA=MAVAcosα·i+MAVAsinα·j+0·k
mB=-MBVB·i+0·j+0·k

(2)

又α=arctan(w′(L,t)),则

(3)

将式(2)、式(3)代入式(1)得非线性势能:

(4)

则磁铁A受到磁铁B作用的非线性磁力为:

(5)

1.2 压电悬臂梁振型

由于压电悬臂梁通常作低频振动,其一阶弯曲振动模态对系统动力学响应特性影响最大。因此,根据Raleigh-Ritz方法可将图1所示压电悬臂梁的振动位移w(x,t)写成:

w(x,t)=φ1(x)q1(t)

(6)

式中:φ1(x)为一阶弯曲模态振型,q1(t)为一阶弯曲广义模态坐标。

式中:

(7)

且振型函数可表示为:

(8)

为计算振型系数C1、C2、C3、C4、D1、D2、D3、D4,可列出以下边界条件:

(9)

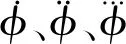
变截面梁两部分的模态频率关系为:

(10)

式中:ω1为一阶模态振型角频率。

1.3 压电能量采集器动力学方程

压电能量采集器的动力学方程采用拉格朗日方程建立,系统拉格朗日函数为[11-12]:

La(x,t)=Ts+Tp+TM+We-Us-Up-Um

(11)

式中:Ts、Tp分别为金属基板和压电片的动能,TM为悬臂梁末端磁铁的动能,Us、Up分别为金属基板和压电片的势能,We为压电片的电能,Um为磁铁对之间的势能。它们的具体表达式如下:

(12)

(13)

(14)

(15)

(16)

(17)

式(11)中的非线性势能Um可将式(4)在q1(t)=0处进行泰勒展开得到,即

Um=a0+0.5a1q1(t)2+0.25a2q1(t)4+o[q1(t)4]

(18)

式中:

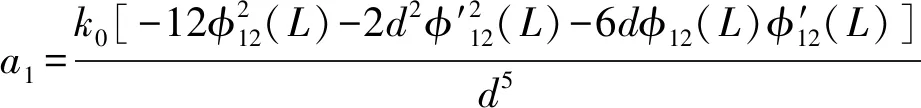
将式(12)～式(18)代入式(11)所示的拉格朗日函数,并考虑系统广义耗散能量得到系统动力学方程为

(19)

将式(19)转换成状态空间方程形式得:

(20)

1.4 谐波平衡法求解动力学方程

(21)

将式(21)代入式(19)中,令方程两边的sin(ωt)、cos(ωt)、常数项系数相同,并且忽略高次谐波项,则有:

C(k+sC2+1.5s(A2+B2))=0

(22)

B(k-ω2+0.75s(A2+B2))+2ξωA-θE+ΓA0=0

(23)

A(k-ω2+0.75s(A2+B2))-2ξωB-θD=0

(24)

E+θωRA+0.5ωCpRD=0

(25)

D-θωRB-0.5ωCpRE=0

(26)

r2=A2+B2

(27)

式中:r为一阶模态振动位移的幅值。

由式(25)、式(26)得

(28)

(29)

将式(28)、式(29)代入式(23)、式(24)后平方相加得:

(30)

由式(22)解得,

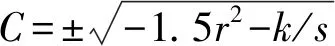
(31)

将C代入式(30)后可以得到能量采集器的振动位移幅值r,并得到能量采集器输出的电压幅值和一个周期内的平均输出功率分别为

(32)

(33)

2 采集器时-频域动力学特性仿真

为了研究双稳态压电振动能量采集器动力学特性对系统参数敏感性,首先研究了系统静态分岔特性以及势能特性。图3所示为能量采集系统静态分岔分析结果,当末端磁铁A和外部磁铁B的中心距d大于分岔点间距d0=36.6 mm时,非线性磁力较小,系统只有一个稳定解,系统变成单稳态系统。当d小于分岔点间距d0时,能量采集器出现分岔现象,有两个稳定的解和一个不稳定的解,且两个稳定解的距离随d的减小先增大后减小。图3所示为能量采集器的势能结果,当d<36.6 mm时,如图4中d=35 mm、30 mm和25 mm时所示,采集器势能曲线出现两个对称的势阱和一个势垒,表现出双稳态特性,并且随着d的减小,势垒逐渐增大。当d大于36.6 mm,如图4中d=40 mm所示,采集器的势能曲线由双势阱退化成一个势阱,表现出单稳态运动特性。

图3 采集器静态分叉特性

图4 采集器势能曲线

2.1 系统时域动力学特仿真分析

2.1.1 加速度幅值A0对动力学特性的影响

图5 d=30 mm,f=5 Hz时采集器的时域动力学特性

根据静态分叉特性和势能特性的分析结果,取磁铁间距d=30 mm,激振频率f=5 Hz,研究激振加速度幅值A0对系统时域动力学特性的影响,结果如图5所示。图5(a)所示为不同激振加速度A0时能量采集器的分岔图,由图可知当A0小于8m/s2的时,系统作单稳态运动,并在某个势能阱内作小幅周期振动,此时采集器的相图为一个圆,且圆心位于某个势能阱中心,如图5(b)所示,采集器的振动位移幅值仅为1 mm;当激励加速度幅值A0增大到8 m/s2～10.5 m/s2,采集器获取的动能增加,系统开始越过势垒,并由单周期小幅值振动进入三周期大幅值振动状态,其相图如图5(c)所示,此时采集器的振动位移幅值和振动速度幅值都急剧增大;继续增大激励加速度幅值A0到10.5 m/s2～14 m/s2,采集器开始作大幅值的混沌运动,其相图如图5(d)所示;当激励加速度幅值A0在14 m/s2～17 m/s2范围内,采集器又进入三周期大幅值振动状态,如图5(e)所示。继续增大激励加速度A0,采集器最后进入大幅值双稳态周期振动,如图5(f)所示。总之,在A0<8 m/s2范围内,采集器在某个势能阱内作小幅值的单周期振动,在A0>8 m/s2时,采集器开始在两个势能阱之间来回作大幅值的振荡,这有利于提高振动能量采集器的输出性能,但对外部激励条件要求较高,需要有足够的激励强度使采集器克服势能阱之间的势垒阻碍作用。此外,图5所示运动现象说明在一定的激励条件下混沌吸引子和周期吸引子可以互相转化,从而是采集器表现出大幅值的振动特性,提高能量采集输出能力。

2.1.2 磁铁间距d对系统动力学特性的影响

取f=5 Hz,A0=8 m/s2,研究磁铁间距对系统分叉特性和动力学特性的影响,如图6所示。由图6所示的分岔图可知,当磁铁间距d<23 mm时,由于磁力势能太大,系统无法越过势垒,采集器被限制某一个势阱内作小幅运动,其相图如图6(b)所示;随着d的不断增大,磁力势能不断减小,系统开始越过势垒在两个势能阱之间来回作大幅的多周期[d=30 mm,图6(c)]和双稳态[d=35 mm,图6(d)]运动;继续增大d,磁力势能继续减小,由于磁力作用减弱,采集器开始进入单稳态周期运动,悬臂梁末端振幅位移幅值也逐渐较小,如图6(e)所示。

图6 A0=8 m/s2,f=5 Hz时采集器的时域动力学特性

2.1.3 激振频率f对系统动力学特性的影响

取磁铁间距d=30 mm,激振加速度A0=8 m/s2,研究激振频率f对系统分岔特性和动力学特性的影响,分别如图7所示。由图7(a)可知采集器系统频率响应向特性非常复杂;在f=5 Hz以内,采集器作周期的大幅值振动,如图7(b)所示为f=4 Hz时作单周期的大幅值振动,图7(c)所示为f=5 Hz时作三周期的大幅值振动;在f=5 Hz～10.5 Hz范围内,采集器作双稳态大幅值振动,如图7(d)所示为f=9 Hz时的双稳态振动相图;当f=10.5 Hz～21 Hz范围内,系统进入混沌状态,如图7(e)和图7(f)所示分别为f=11 Hz和f=21 Hz时的混沌振动相图;当f大于21 Hz时,系统作小幅振动,如图7(g)为f=22 Hz时的二周期小幅振动相图;当f大于32 Hz时,采集器系统作小幅值单稳态周期运动,如图7(h)所示为f=35 Hz时的小幅值单稳态相图。从图7所示结果可以看出,压电能量采集器作大幅值振动的频带范围为4 Hz～21 Hz。

图7 A0=8 m/s2,d=30 mm时采集器的时域动力学特性

2.2 系统频域动力学特仿真分析

本节利用谐波平衡法进行仿真,研究改变系统外部激励(激振频率、激振加速度)、磁铁之间的距离、负载电阻时对系统输出功率的影响。

2.2.1 采集器幅值-频率特性

图8所示时A0=10 m/s2时不同磁铁间距d=[20 26 30 45]mm下的采集器末端振动幅值-频率响应r-f曲线。图中r小于0.5 mm为小幅阱内运动,r大于0.5 mm为大幅阱间运动。由图8可知采集器的大幅运动和小幅运动可以共存,大幅运动振幅随着f的增加而增加,且向右倾斜,表现出软特性;小幅阱内运动主要集中在f=30 Hz～40 Hz,并且由于磁力引起的非线性刚度,频率响应曲线向左倾斜,表现出硬特性。此外,随着磁铁间距d的增大,大幅阱间运动频率范围减小,振幅最大值增大,小幅阱间运动频率范围左移。

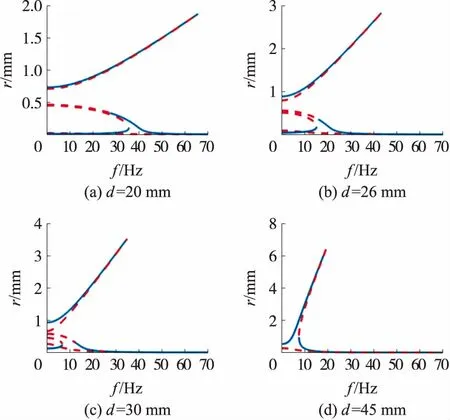
图8 采集器幅值-频率响应(实线为稳定解,虚线为不稳定解)

2.2.2 采集器输出功率特性

图9所示为f=5 Hz,R=7 MΩ,d=25 mm时激振加速度幅值与采集器输出功率的关系。由图9(a)可知当激振加速由小变大时功率缓慢增长,当激振加速到50 m/s2时,输出功率突然变大,之后又缓慢增长,这是因为在刚开始振动幅值很小,悬臂梁振动位移和振动速度小,系统动能小于势能,悬臂梁无法越过势垒;当激振及速度不断增大,其动能不断增大,待动能大于势能时才越过势垒进入大幅振动状态;反之,当激振加速度由大变小时,输出功率先缓慢变小,随着激振加速度的不断减小,当A0大约为1 m/s2时,功率急剧下降,因为刚开始时激振加速度比较大,其动能也大,轻松越过势垒作大幅阱间运动,因为其振动速度大,导致输出功率也大,当A0<1 m/s2时,因动能太小无法越过势垒,从而作小幅阱内运动。图9(b)和图9(c)分别给出了在大幅振荡的情况下,不同磁铁间距d=[20,25,30]mm时的输出功率P随激振加速A0的变化曲线。由图9可知在阱间运动情况下输出功率增长的速率随d的增大而增大。

图9 采集器输出功率随激振幅值的变化情况(实线为稳定解,虚线为不稳定解)

图10是在大幅振荡的情况下,激振频率f=[4,8,12]Hz,A0=4 m/s2,d=30 mm时,输出功率随电阻的变化曲线,图10可知,采集器输出功率随电阻的增大先增大后减小;当频率增大,最优阻抗随激振频率增大而减小,最大输出功率随激振频率增大而增大。

图10 不同激励频率下输出功率随负载电阻的变化

图11是在大幅振荡的情况下,激振加速度A0=[4,10,15]m/s2,d=30 mm,f=8 Hz时输出功率随电阻的变化曲线,由图11可知,最优阻抗并不会因为激振加速度改变而改变,但是最大输出功率却随激振加速度增大而增大。

图12是在大幅振荡的情况下,磁铁间距d=[10,20,30]mm,A0=4 m/s2,f=8 Hz时输出功率随电阻的变化曲线,由图可知,在R=7 MΩ时采集器输出功率达到最大,最优阻抗并不会因为磁铁距离的改变而改变,但是最大输出功率却随磁铁之间距离的增大而减小。

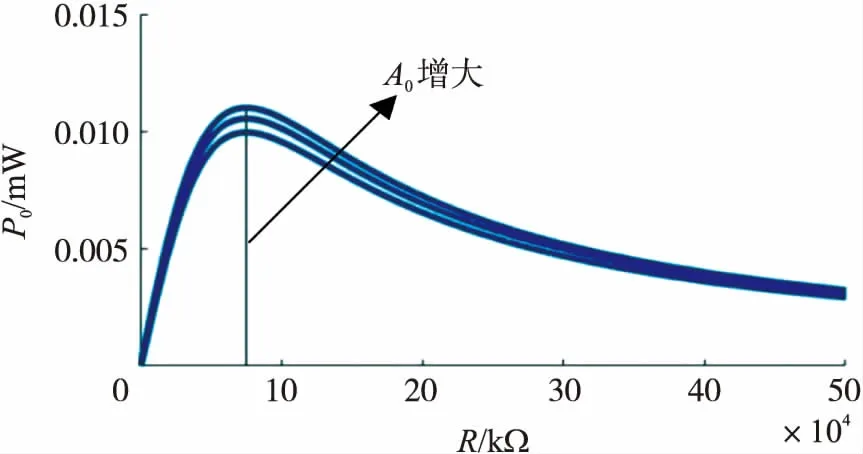
图11 不同激励幅值下输出功率随负载电阻的变化

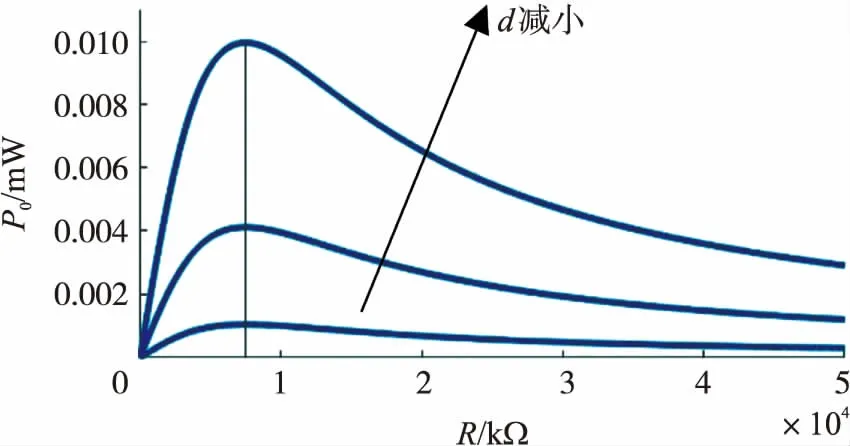
图12 不同d下输出功率随负载电阻的变化

图13 实验测试系统

3 实验验证与结果分析

3.1 样机与实验系统

为了验证双稳态压电振动能量采集系统参数对其时-频域动力学特性的影响的正确性,搭建了实验测试平台,如图13所示。实验样机的悬臂梁尺寸为70 mm×10 mm×0.15 mm,如图14所示,悬臂梁末端用高强度胶粘结一永磁铁,另一个外部磁铁也通过高强度胶粘结在基座上;两片压电片(PZT-5A)通过高强度胶经高温固化后粘结在金属基体的上、下表面,PZT表明通过金属铜电极串联连接负载电阻R。实验中,双稳态压电能量采集器样机通过夹具安装在激振器(JZK-5)的测试台上,信号发生器(AFG3102C)产生的正弦信号经功率放大器(YE5871A)放大后,使激振器产生正弦振动;基础加速度由加速度传感器(YJ9A)测量得到,悬臂梁末端位移由激光位移传感器(LK-G80)测量得到通过软件在电脑上显示,悬臂梁末端振动速度由激光测速仪(Polytech OFV-505)测得,采集输出电压由示波器测得和显示。

图14 悬臂梁样机

3.2 实验结果分析

根据仿真分析结果,选取磁铁间距d=[26、30]mm,f=4.95 Hz,分别逐渐增大(正向扫描)和减小(反向扫描)激振加速度幅值,测量采集器的输出功率有效值,实验结果如图15所示。由图15可知,当d=26 mm时,正向增大激励加速度幅值到51 m/s2,采集器由小幅值的单稳态运动跳转到大幅值的双稳态运动,这与图9(a)所示仿真计算结果50 m/s2是吻合的,说明仿真计算结果是正确的。当反向减小激励加速度幅值时,采集器输出功率逐渐减小,当到加速度幅值减小到5 m/s2时,采集器由大幅值振动状态跳转到小幅值振动;同理,当d=30 mm时,采集器由小幅值振动跳转到大幅值振动的激励加速度幅值为19 m/s2,这与图9(b)所示的仿真计算结果20 m/s2是吻合一致的。此外,由图13所示的实验结果还可以看出,增大磁铁间距d,采集器由小幅值振动跳转到大幅值振动所需要的激励加速度幅值也减小,增大激振加速度采集器的突跃点左移,减小激振加速度,采集器的突跃点右移,这与图9所示数值仿真的趋势相似,仿真得以验证。

图15 采集器幅值-功率特性实验结果

图16是激振频率f=4.95 Hz,激振加速度为A0=15 m/s2时,不同磁铁之间的距离d=[26、28、30]mm下采集器输出功率Prms随负载电阻R的变化情况实验结果。由图可知,随着电阻的增大,功率先增加到一个峰值,然后持续下降;功率随着d的增大而减小,但是最优阻抗在d的改变下不变,为1.1 MΩ,趋势与图12所示数值仿真一致。

图16 不同d下输出功率随负载电阻的变化实验结果

图17所示为磁体间距离d=28 mm,A0=10 m/s2,采集器在频率f=[13 16]Hz时的输出功率Prms随负载电阻R的实验变化结果。由图可知,功率随着激振频率f的增大而增大,且最优阻抗随着激振频率f增大而减小,实验结果趋势与图10仿真结果趋势相似。

图17 不同激励频率下输出功率随负载电阻变化的实验结果

图18是磁体间距d=28 mm,f=4.95 Hz,采集器不同激振加速度下的输出功率Prms随负载电阻R的变化实验结果。由图可知,功率随着A0的增大而增大,且最优阻抗不变,实验趋势与图11所示数值仿真结果相似。

图18 不同激励幅值下输出功率随负载电阻的变化实验结果

为了进一步验证仿真结果的正确性,取激振频率为f=11 Hz,d=26 mm,逐渐增大激振加速度,测量双稳态压电发电系统不同激振加速度下的运动特性,结果如图19所示。

图19 d=26 mm,f=11 Hz时采集器的时域动力学特性实验结果

图19(a)为激振加速度幅值A0=10 m/s2时的相图实验结果,此时为小幅周期振动;图19(b)为A0=20 m/s2时的相图,此时采集器先作大幅值的双稳态运动后进入混沌运动,继续增大A0=30 m/s2,如图19(c)所示,此时采集器则完全进入混沌运动状态;继续增加A0=45 m/s2,采集器则作大幅周期振动,如图19(d)所示。上述实验得到的运动特性变化趋势与图5所示仿真结果趋势是相似的。

4 结论

建立了双稳态压电振动能量采集器的非线性磁力模型和机电耦合动力学方程,并通过谐波平衡法求解动力学方程的解,实验结果验证了仿真结果的正确性,得到以下结论:①改变磁铁的间距会使系统由单稳态变为双稳态;双稳态系统在低频率范围内会出现大幅运动,且响应频带很宽。②系统存在大幅运动吸引子,一定情况下改变激振频率以及激振加速度可以实现混沌吸引子和周期吸引子之间的转化。③最优阻抗主要由激振频率决定,激振加速度和磁铁间距对其影响甚微。