一种高精度时差法超声波水表的设计与实现*

王磊阳,陈建峰,刘明祥,张 凯

(中国计量大学计量测试工程学院,杭州 310018)

传统机械水表是以机械元件为主要部件,采用叶轮旋转的计量方式计量用水量,存在计量灵敏度低、压力损失大、抄表困难等不足,且其内部为接触式测量,测量元件长期磨损会导致机械水表的计量精度和稳定性下降,检定周期和维修周期短。机械水表已难以满足现代社会和人们日常生活的要求。

随着智慧水务和物联网技术的发展,超声波水表应运而生。超声波水表采用全电子化设计,无机械运动部件,能够实现较宽的量程比和低区流量的测量,且能满足各类通讯和无线组网的要求。与传统的机械水表相比,超声波水表具有非接触式、压损小、精度高、功耗低、使用寿命长等突出优点,必将成为下一代智能水表的重要选择。

超声波水表所采用的超声波测量技术有多种方法,常用的测量方法有时差法、相关法、噪声法、多普勒法和波束偏移法等。近年来,研究人员开展了基于超声波技术的流量计和超声波水表的研究并取得了显著进展。目前的超声波水表实现方案一般具备温度补偿[1-2]等功能,数据滤波采用小波算法[3]、滑动平均算法[4]等。这些研究成果对于提升超声波水表的测量精度,推动超声波水表的实用化起到了重要的作用。

但是,在系统总体设计方面,现有超声波水表设计少有能同时兼具温度补偿、低功耗和高精度滤波功能,且数据滤波后在低区流量点的精度尚有待提高。为了进一步提升超声波水表的综合性能,本文设计并实现了一种基于时差法和数据滤波的新型超声波水表,具有温度补偿和低功耗运行等功能,提出了一种结合卡尔曼滤波与算术平均滤波的高精度数据滤波算法,明显改善了测量性能,特别在低区流量下具有更高的测量精度,能够更好地满足实际工程应用的需求。

1 系统总体设计

1.1 总体方案

图1示出了高性能时差法超声波水表的系统总体设计方案。

图1 系统总体框图

当管道中有水流时,首先激发超声波换能器,使得超声波信号在管道内沿着水流方向顺流和逆流传播;接着进入信号处理阶段,通过计算超声波信号顺流和逆流传播的时间并相减得到时差信号,时差信号经过新型数据滤波算法和温度补偿后,计算得到流量值;最后进行数据显示与存储。

为了实现精确计量和低功耗等目标,在硬件系统的主控芯片选型上着重考虑高精度运算、低功耗运行和低成本实现,同时选用高精度的计时芯片;在软件方面着重考虑系统功能实现的稳定性、完善性和鲁棒性;在算法实现方面优选了时差法超声波测量法,并提出结合卡尔曼滤波和算术平均的数据滤波,以有效提升计量精度。

1.2 时差法超声波测量原理

超声波流量计测量示意图如图2所示。经研究比较,本文采用时差法进行测量[5]。超声波在流体中传播时,超声波传播的速度是超声波在流体中的波速与流体流速的叠加。时差法超声波测量的基本思路是:产生的超声波信号在流体顺流与逆流传播时的传播速度不同,进而产生传播时间差值。由于时间差值的大小与流速大小有关,因此,通过测量时间差值的大小就可以间接地测量流体的流速[6-7]。

图2 超声波水表测量示意图

换能器P1为顺流换能器,P2为逆流换能器,规定图2中向右为正向,换能器发射出的超声波与流体流向垂直;换能器与反射片的距离为s,超声波在水中的速度为c,反射片与水平面夹角为45°,两反射片的中心距离为L,管道直径为D,水的正向流速即线速度vl为v,则由P1发射、P2接收超声波的顺流时间为:

(1)

而由P2发射、P1接收超声波的逆流时间为:

(2)

由式(1)和式(2),可以求出顺逆流时间差TTD(Transit Time Difference)即Δt为:

(3)

式中:由于在水中超声波声速远大于流体流速,即c2≫v2,因此可近似将分母中的c2取代c2-v2。由此可以得到线速度vl:

(4)

在计算瞬时流速和流量时,用到的是面平均流速。根据流体力学的相关知识,面平均流速根据流体的不同状态,有着不同的修正系数。设修正系数为K,则流体的累计流量Q为:

(5)

根据式(4)可以发现,当顺逆流时间差Δt越大时,水流线速度越大,于是一定时间内的累计流量越大;根据式(5)可以发现,在修正系数K、管道直径D、反射片距离L确定的情况下,一定时间内的累计流量Q只与时间差Δt和超声波传播速度c有关,因此,时间差值和超声波声速的测量成为超声波流量计的关键所在[8-9]。

2 硬件设计

2.1 硬件总体

图3示出了系统的硬件框图。

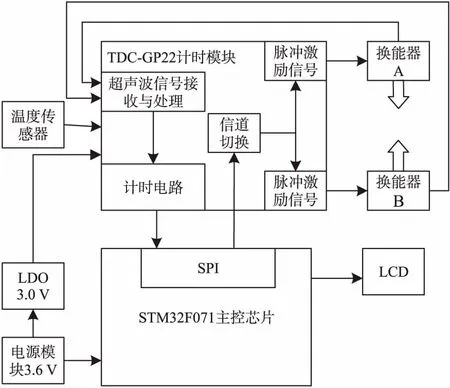
图3 系统硬件框图

系统主要由主控芯片、超声波换能器、温度传感器、计时芯片、LCD显示模块、电源模块等组成。

主控芯片选用内核是Cortex-M0的STM32F071芯片,可以满足运算精度、运算量和低功耗等要求;计时芯片选用TDC-GP22高精度计时芯片;系统采用3.6 V电池供电,经过LDO稳压芯片HT7530输出电压3.0 V,为计时芯片TDC-GP22供电。温度传感器与TDC-GP22直接相连,以进行温度测量。

STM32F071与TDC-GP22通过SPI的通信方式进行通信,用于配置TDC-GP22内部寄存器和触发TDC-GP22进行测量[10]。TDC-GP22内部集成了信道切换电路、脉冲激励电路、超声波信号接收与处理电路、计时电路等。其中,信道切换电路用于切换脉冲激励通道,脉冲激励用于激发超声波换能器产生超声波信号,超声波信号接收与处理电路用于接收超声波信号,以精确确定超声波到达的时间[11]。

2.2 TDC-GP22电路图

本文采用TDC-GP22高精度时间数字转换芯片进行时间差测量和温度测量,TDC-GP22的时间分辨率高达22 ps。图4示出了TDC-GP22的外围电路,包括高速晶振、低速晶振、温度传感器接口、超声波换能器UP接口与超声波换能器DOWN接口以及SPI通信接口等。

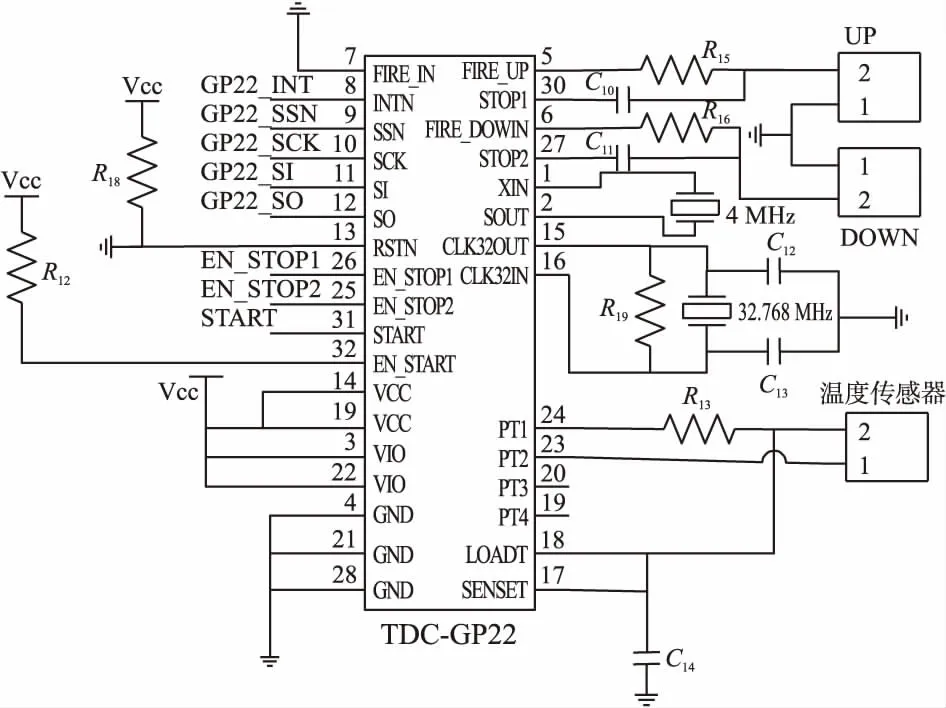
图4 TDC-GP22外围电路

低速晶振选用32.768 kHz作为TDC-GP22的基准时钟,用来控制整个芯片的工作时序以及低功耗模式时的工作时序。高速晶振选用4 MHz陶瓷晶振,陶瓷晶振具有起振时间短、价格低等优势,4 MHz高速晶振用于时差测量,在发送超声波脉冲前起振,在接收到设定的超声波包络信号后停止工作,这种设定可以大大节省功耗。

温度的改变会影响超声波的声速,进而导致测量产生误差,因此本系统集成了NTC(Negative Temperature Coefficient)型具有负温度系数的热敏电阻。

电容充满电后的放电时间与电阻值、电容值有关。温度测量是基于电阻对电容的放电时间的。因此电容将会分别对于参考电阻和温度传感器电阻进行放电。TDC-GP22通过检测C14对R16和NTC的放电时间,会自动在结果寄存器中得到NTC与R16的电阻值之比[12]。

主控芯片读取NTC与R13的电阻值之比,查询温度表格,得到目前传感器的温度,并在主控芯片内部建立声速与温度对应关系,来得到对应的超声波声速值,提高测量精度。

3 软件设计

3.1 软件系统设计

在超声波水表中,STM32F071主控芯片控制整个系统的逻辑时序,图5示出了整个系统的软件流程。

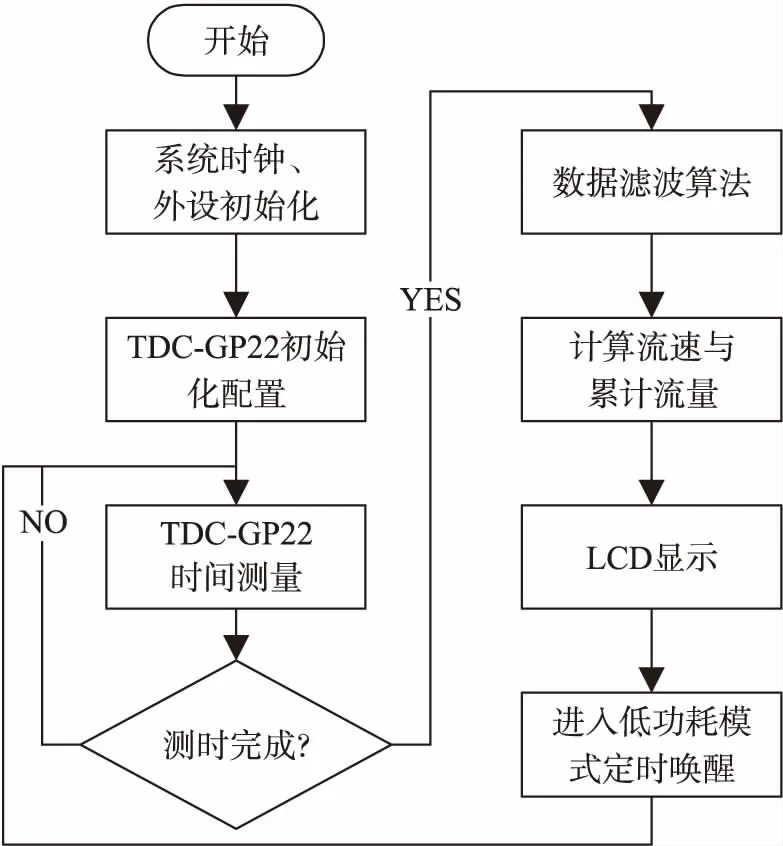
图5 软件流程图

首先系统上电后进入时钟初始化配置,然后对GPIO、SPI、UART、LCD、TIM、RTC、中断、低功耗运行等进行初始化;再通过SPI通信的方式,对TDC-GP22进行初始化并配置内部寄存器;接着进入时差测量程序,当测量完成后,运行滤波算法对数据进行处理,完成后进行温度补偿、计算流速和累计流量,并通过LCD显示,将累计流量存储至主控芯片内部FLASH,以防止掉电丢失;最后进入低功耗STOP模式,等待RTC定时到达下次唤醒。

低功耗设计是软件设计的重点。STM32F071在STANDBY和STOP两种模式下的功耗都小于1 μA,TDC-GP22计时芯片的功耗在静态下也仅为2.2 μA。进入低功耗模式后,唤醒并进行流量测量的频率为超声波水表的采样频率,本文设定采样频率的大小与流速变化量有关,当认为流速处于稳定状态时,设定采样频率为1 Hz,即1 s钟测量一次,其余时间处于休眠状态;当流速变化量增加时,增加采样频率,增加量与流速变化量成正比例关系。

3.2 数据滤波

数据滤波处理是为了去掉原始数据中的随机误差,以提高数据质量的一种方法[13]。在超声波水表系统中,由于测量过程会引入噪声,使得测量结果与实际流速值产生一定偏差。偏差值的大小与流体中是否有气泡或颗粒物、超声波信号质量、电路板PCB布局、温度补偿超声波声速值误差、外部电磁干扰等有关。为了减少外部噪声对超声波水表的干扰,提高水表的精度,本文提出一种卡尔曼滤波算法与算术平均算法结合的新型数据滤波算法。

3.2.1 卡尔曼滤波

卡尔曼滤波(Kalman Filtering)是一种最优线性状态估计方法,当流速变化率处于一定范围内时,处于稳定状态,可以使用卡尔曼滤波来对数据进行滤波,一般迭代过程如下[14-17]:

①预测现在状态

x(k|k-1)=A·x(k-1|k-1)+B·U(k)

(6)

式中:A和B是系统参数,对于多模型系统,它们为矩阵,x(k|k-1)是利用上一状态预测的结果,x(k-1|k-1)是上一时刻的最优预测值,U(k)为现在状态的控制量,流量稳定时,设定A、B、U(k)为0。

②更新协方差

P(k|k-1)=A·P(k-1|k-1)AT+Q

(7)

式中:P(k|k-1)是x(k|k-1)对应的协方差,P(k-1|k-1)是x(k-1|k-1)对应的协方差,AT是A的转置矩阵,Q是系统噪声。

③计算Kg值

Kg(k)=P(k|k-1)H(k)T·
[H(k)(P(k|k-1)+R)]-1

(8)

式中,Kg为卡尔曼增益(Kalman Gain),R为测量过程中的噪声,H(k)是测量系统的参数。

④参考测量值进行估计

x(k|k)=x(k|k-1)+Kg(k)·
[Z(k)-H(k)x(k|k-1)]

(9)

式中:x(k|k)是通过参考测量值得到的最终估计值,Z(k)是k时刻的系统测量值。

⑤更新k时刻的协方差

P(k|k)=[1-Kg(k)H(k)]·P(k|k-1)

(10)

式中:P(k|k)是x(k|k)对应的协方差。

3.2.2 数据滤波算法

图6示出了卡尔曼滤波算法与算术平均算法结合的数据滤波算法。首先,快速测量八组流量数据并储存,判断其最大值与最小值的差值,当超声波水表检测到有流速增加大于或等于一定阈值δ时,此时认为水的流量处于快速变化阶段,提高超声波水表采样频率Fs,同时进入算术平均滤波算法阶段。当检测到流速增加值小于一定阈值范围δ内,此时认为水流量处于稳定状态,则减小采样频率Fs,并进入卡尔曼滤波算法阶段。

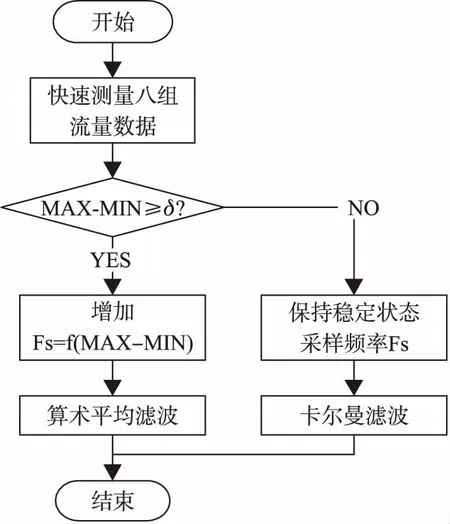
图6 数据滤波算法

采用卡尔曼滤波算法与算术平均算法结合的方法可以有效提高超声波水表在水流稳定状态时的精度,同时能极大克服卡尔曼滤波后的流速值跟随真实流速值变化能力差的缺点。不仅能提高超声波水表在水流稳定状态下的计量精度,降低零点漂移,而且使得流量处于非稳定状态时的计量精度有一定的提升。总之,采用卡尔曼滤波算法与算术平均算法结合的方法能有效提高超声波水表的精度。

4 实验结果与分析

4.1 实验设置

超声波水表样机如图7所示。该样机主要由超声波换能器、电路板、LCD、管道、电池等组成。

图7 超声波水表样机

为了精确地测试超声波水表的计量性能,参照《JJG-162-2009-冷水水表检定规程》,采用容积法水流量检定装置进行流量检定以及瞬时流量和累计流量等的测试。

测试检定环境如图8所示。试验台分辨率为千分之一,精度为±0.2%,可用于检定小口径超声波水表,可串联检测5表位。该装置主要由水泵、水稳压管、不同口径阀门、标准表、标准容器、水池等部分组成。

图8 检定环境

测试检定时,先安装好被检表,然后打开水泵,调节流速,根据标准表的显示示数调节到不同的流量大小,并根据被检表的示数来判断测量准确性。

4.2 实验数据

小管径超声波水表的设计量程范围为0.015 6 m3/h至3.125 m3/h,R值选取160,管径为DN15,精度等级为1.5级。

按照《JJG-162-2009冷水水表检定规程》,检定流量点分别为Q1、Q2、Q3、Q4,其中Q1的实际流量控制在Q1～1.1Q1之间,Q2的实际流量控制在Q2～1.1Q2之间,Q3的实际流量控制在0.9Q3～Q3之间。共测试4个流量点,对每个流量点测试6次,取平均,实验结果如表1所示。

为了验证数据滤波算法的效果,本文随机选取了分布在低区(流量低于分界流量Q2)和高区(流量大于分界流量Q2)的某两个流量点,测试若干组数据滤波前后的时差数据,选取了五组数据,分别如表2和表3所示。并且随机选取了某个流量点,测试数据滤波前后的时差数据以直观地展示数据滤波算法的效果,数据滤波前和数据滤波后的结果分别如图9和图10所示。

表1 累积流量数据

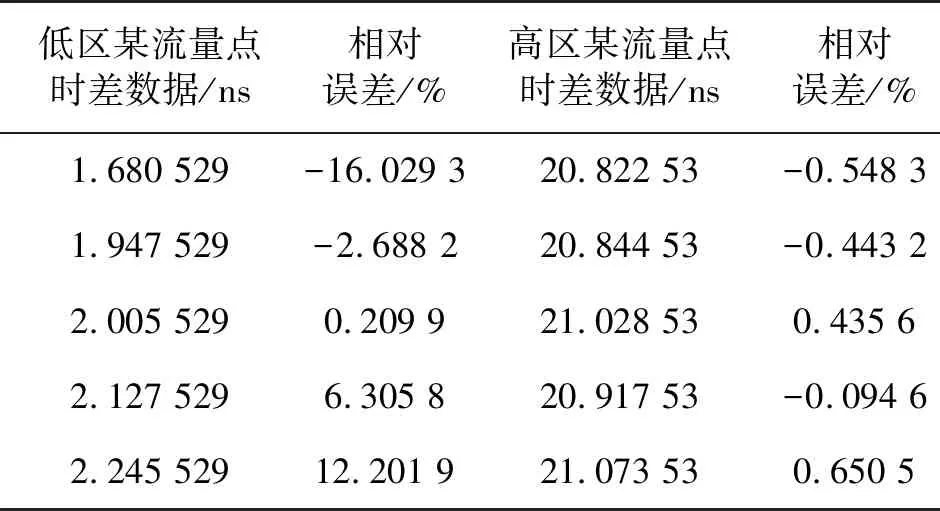
表2 数据滤波前的时差信号样本

表3 数据滤波后的时差信号样本

图9 数据滤波前的时差信号

图10 数据滤波后的时差信号

4.3 数据分析

表1是累计流量实验数据,按照《JJG-162-2009 冷水水表检定规程》,精度等级为1.5级表的累计流量在低区Q1、Q2点不能超过±3%,在高区Q3、Q4不能超过±1.5%。表中,在Q1为-2.00%,在Q2、Q3、Q4点的误差均小于1%,均满足1.5级表的精度等级。

表2示出了数据滤波前某低区流量点和某高区流量点的五组时差信号,表3示出了数据滤波后某低区流量点和某高区流量点的五组时差信号。表2与表3中的低区流量点数据和高区流量点数据为超声波水表在同一时间通过串口打印方式分别将数据滤波前和数据滤波后的时差信号打印出来的时差数据。

表中,计算相对误差的公式为:

(11)

式中,δ为实际相对误差,一般用百分数给出,Δ为绝对误差,即真值与测量值之差,L为(约定)真值,实际计算中以均值替代真值。

从表2中可以看到,当稳定流量处于高区时,绝对误差Δ在一定范围内波动,但是时差信号的真值L较大,根据式(11)可知,此时相对误差较小。而当稳定的流量处于低区时,绝对误差Δ在一定范围内波动,且时差信号的真值L较小,根据式(11)可知,此时相对误差δ较大,难以实现精确计量。

为了更好地对比表2与表3中的时差信号样本数据,计算了表2与表3中低区和高区流量点的时差数据的样本均值以及相对误差最大值与最小值之差(MAX-MIN),结果如表4所示。

表4 数据滤波前后的性能比较

从表4中的对比可以发现,数据滤波在低区某流量点下的效果更为显著,五组样本数据相对误差的最大值与最小值之差(MAX-MIN)由数据滤波前的28.231 2%降至数据滤波后的0.955 0%。数据滤波在高区某流量点下也有一定的效果,五组样本数据相对误差的最大值与最小值之差(MAX-MIN)由数据滤波前的1.198 8%降至数据滤波后的0.047 6%。

图9和图10分别示出了某一稳定流量点下在数据滤波前后的时差信号。从图中可以看出,数据滤波后的时差信号相对于数据滤波之前的时差信号更加平滑。为了描述数据滤波前后时差信号的离散程度,引入方差的定义:

(12)

方差和标准差是测算离散趋势最重要、最常用的指标,方差或标准差和越大,则表示样本越分散。计算得到数据滤波前的标准差为0.053 44 ns,数据滤波后的标准差为0.029 54 ns,数据滤波后的标准差较数据滤波前降低了44.7%,说明数据滤波后的数据更加稳定,精度更高。

4.4 零点漂移分析

为了测试对比数据滤波算法的效果,在标准室温和检定环境下,采样了原始时差数据、经过滑动平均滤波算法的时差数据、经过卡尔曼滤波结合算术平均滤波算法的时差数据各100组,分别标记为样本1、样本2、样本3。

图11是室温下采集的超声波水表零点漂移数据,系统零点漂移范围保持在±0.4 ns以内。图12是经过滑动平均滤波算法后得到的零点漂移数据,该算法可以有效地降低系统零点漂移,系统零点漂移范围降至±0.1 ns以内。图13是经过卡尔曼滤波结合算术平均滤波后得到的零点漂移数据,系统零点漂移范围达到±0.03 ns以内。对比图12和图13可以看出,采用本文滤波算法,系统零点漂移仅为滑动平均算法的1/3,滤波性能明显提高。

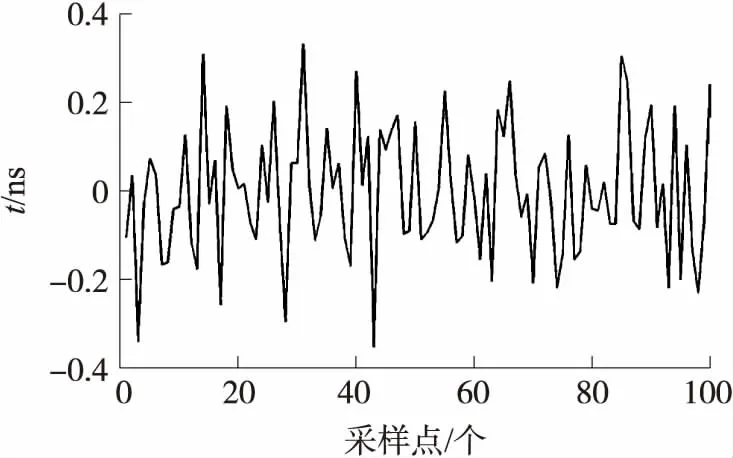
图11 零点漂移

图12 滑动平均滤波后的零点漂移

图13 卡尔曼滤波结合算术平均滤波后的零点漂移

为了更好地分析三组样本数据,表5分析了三组样本的最大值与最小值之差和标准差[18]。最大值与最小值之差的大小表示样本数据的范围大小,样本数据范围越小表示数据越稳定;而标准差越小,则表示样本分散程度越低。从表5可以看出,样本3的最大值与最小值之差和标准差都最小,样本2次之,而样本1则最大。表5结果表明样本3的数据最为稳定,且分散程度最低。

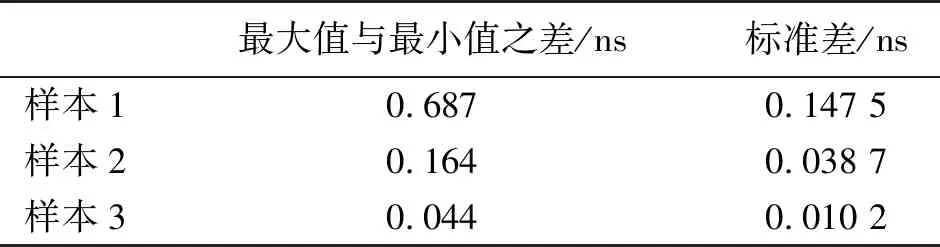
表5 零点漂移数据分析

从以上分析可以得出,本文数据滤波算法能够有效地降低超声波水表的零点漂移,提高测量精度,特别是能够提高低区的测量精度,与滑动平均滤波算法相比,本文算法的数据稳定性更高,滤波效果更好。

5 结束语

为了克服传统机械式水表存在的问题,本文设计并实现了一种高性能时差法超声波水表。系统的主控芯片选用STM32F071,采用TDC-GP22进行时间和温度测量。提出了一种卡尔曼滤波与算术平均结合的数据滤波算法,降低了零点漂移,提高了测量精度。数据滤波算法的使用能够有效滤除噪声干扰,降低时差信号相对误差,在低区作用更为显著。测试结果表明,本文研制的超声波水表的综合性能够满足实际应用需求。