《倍的认识》教学实践与思考

索昂措毛 吕琼华

【教学内容】

人教版三年级上册第50 页。

【教学过程】

一、提出问题，引出“倍”

1.提出问题。

师：仔细观察下图，你获得了哪些信息？能提出哪些数学问题？

生：图中有几只兔子？白兔和灰兔各有几只？哪种兔子多？一共有几根萝卜？胡萝卜、水萝卜、白萝卜各有几根？哪种萝卜最多？

2.动手操作。

出示学习要求：

（1）摆一摆：用黄圆表示白兔，用粉圆表示灰兔，一只兔用一个圆表示。用红圆表示胡萝卜，用蓝圆表示水萝卜，用绿圆表示白萝卜，一根萝卜用一个圆表示。

（2）说一说：谁多谁少，为什么？

3.反馈与交流。

（1）反馈用圆片表示兔子的方法，并说一说发现。

生：白兔有3 只，灰兔有3只。白兔和灰兔一样多。

（2）反馈用圆片表示萝卜的方法，说一说发现。

生：胡萝卜有2 根，水萝卜有6 根，白萝卜有10 根；胡萝卜、水萝卜和白萝卜一共有18 根。

生：水萝卜比胡萝卜多4 根，胡萝卜比水萝卜少4 根；水萝卜比白萝卜少4 根，白萝卜比水萝卜多4 根；胡萝卜比白萝卜少8根，白萝卜比胡萝卜多8 根。

4.揭题。

师：两个数量之间除了比多、比少这样的相差关系外，还有另一种关系——倍的关系。今天我们就来认识这个新朋友——倍。

【设计意图：从学生喜欢的情境入手，引导学生提出相并关系和相差关系的数学问题，通过比较不同萝卜的数量，引出“倍”的概念，初步感知“倍”也是表达两种量之间的关系的。同时，通过用圆片表示兔子和萝卜的数量，培养学生的符号意识。】

二、自主探究，理解“倍”

1.初步建立“倍”的概念。

（1）认识3 倍。

师：如果把2 根胡萝卜看成1 份（圈出1 份），水萝卜的根数中有“几个2”呢？

生：水萝卜有3 个2。

师：你是怎么知道的？

生：（一边圈一边数）1 个2，2个2，3 个2。

师：2 根胡萝卜是1 份，水萝卜有这样的3 份，我们就说水萝卜的根数是胡萝卜的3 倍。

（2）认识5 倍。

师：找一找哪两个数量之间也有倍数关系？你是怎么想的？

生：白萝卜的根数是胡萝卜的5 倍。

师：你是怎么知道的？

生：因为2 根胡萝卜为1 份，白萝卜有5 个2，所以白萝卜的根数是胡萝卜的5 倍。

师：（增加2 个绿圆）如果白萝卜增加2 个，现在可以怎么说？

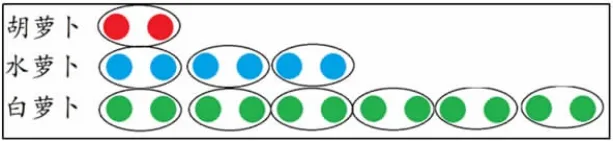
生：白萝卜的根数是胡萝卜的6 倍，因为2 个为1 份，白萝卜有这样的6 份。

师：如果再增加2 根白萝卜呢？

生：白萝卜的根数是胡萝卜的7 倍。

师：再增加2 根白萝卜呢？

生：白萝卜的根数是胡萝卜的8 倍。

师：你发现了什么？

生：有几个2 就是2 的几倍。

师：非常好，2 个为1 份，有几个2，就是2 的几倍。

【设计意图：以2 为标准，在“几个2”的知识基础上，帮助学生初步认识“倍”的概念，符合学生的认知规律和思维特点。】

2.进一步理解“倍”。

师：如果增加1 根胡萝卜，能找到胡萝卜、水萝卜和白萝卜之间的倍数关系吗？请按要求学习：

（1）完成《学习单》。

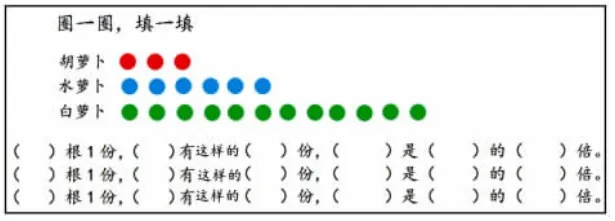
（2）同桌交流想法。

（3）交流反馈。

师：仔细观察，你发现了什么？

生：刚才都是2 根胡萝卜为1 份，现在是3 根胡萝卜为1 份。

师：很好，为什么会发生变化？

生：因为以胡萝卜为标准，3根胡萝卜是1 份，所以水萝卜和白萝卜都要3 根1 份。

师：它们之间的倍数关系呢？

生：3 根胡萝卜是1 份，水萝卜有这样的2 份，水萝卜的根数是胡萝卜的2 倍。白萝卜有这样的4 份，白萝卜的根数是胡萝卜的4 倍。

生：我的圈法和大家不一样。

师：非常好，谁能说说这幅图中的倍数关系吗？

生：6 根水萝卜是1 份，白萝卜有这样的2 份，白萝卜的根数是水萝卜的2 倍。

师：为什么白萝卜刚才是4倍，现在又变成2 倍了？

生：因为比较的标准不同，刚才是和胡萝卜比，3 根1 份，有4份，所以是胡萝卜的4 倍；现在是和水萝卜比，6 根1 份，有这样的2 份，所以是水萝卜的2 倍。

师：很棒，看来比较的标准不一样，比较的结果也会不同。

【设计意图：通过变换标准量和比较量，让学生明确谁是谁的几倍，就是看清哪两个量在比，谁为标准，比的标准不同了，结果就不同了。在变和不变中，既让学生经历了“倍”这个概念的发生和形成过程，又渗透了函数变化的思想，加深了对倍的理解。】

三、动手操作，实践“倍”

1.摆一摆。

（1）出示要求：第一行摆黄圆，第二行摆红圆，红圆的个数是黄圆的3 倍。

（2）学生摆一摆。

（3）反馈交流。

教师呈现如下几组作品，引导学生思考不同摆法之间的异同以及原因。

通过交流，学生发现：

不同点：黄圆的个数不一样，红圆的个数也不一样。

相同点：红圆的个数都是黄圆的3 倍。

原因：2 个1 份，3 个2 是6；3 个1 份，3 个3 是9；4 个1 份，3个4 是12；尽管都是3 份，因为1份数黄圆的个数不一样，所以红圆的个数也不一样。

2.画一画。

（1）出示要求：下图每行都有6 个圆，请你涂上红色，使第二行的红圆个数是第一行的倍数。有几种不同的方法都画下来。

（2）学生独立活动。

（3）交流。

第一种思路：第一行画1 个，第二行可以画1 个、2 个、3 个、4个、5 个、6 个；第一行画2 个，第二行可以画2 个、4 个、6 个；第一行画3 个，第二行可以画3 个、6个；第一行画4 个，第二行可以画4 个；第一行画5 个，第二行可以画5 个；第一行画6 个，第二行可以画6 个。

第二种思路：1 倍关系（6 种画法）；2 倍关系（3 种画法）；3 倍关系（2 种画法）；4 倍关系（1 种画法）；5 倍关系（1 种画法）；6 倍关系（1 种画法）。

【设计意图：练习的设计突出了层次性、多样性。“摆一摆”的活动，通过变化一倍数和几倍数使倍数不变，让学生体验变与不变的辩证思想，深入理解“倍”这个概念的关键。“画一画”的活动更开放，为学生提供了拓展的空间，尤其是通过有序地呈现不同的画法，并对不同画法进行对比分析，使学生在比较中进一步体会“倍”的概念。】

四、回顾总结，说说“倍”

师：今天学习了什么知识？你有哪些收获？还有什么问题？

【设计意图：课堂总结部分通过三个问题，引发学生对“倍的认识”进行回顾和反思。既整理了知识，又思考存在的问题，培养学生对知识的整理归纳和反思的能力以及问题意识。】

从“比多少”这种绝对数量的比较到“倍”这种相对数量的比较，学生在认知结构上是一个质的飞跃。“倍”作为一个数学概念，其核心是抽象，教学中，从实物——圆片——数的顺序来认识倍，呈现了从具体到半抽象再到抽象的过程，符合学生的年龄特征和认知水平。整节课通过摆一摆、圈一圈、画一画等操作活动帮助学生积累表象，并通过观察、比较、变化、抽象等数学活动让学生经历“倍”这个概念的发生过程，经历建构倍的直观模型的过程，最终把握和理解“倍”的本质属性。