基于大数据的瓦斯报警甄别研究

杨建全1，李 筱，李雅斌

(1.平顶山天安煤业股份有限公司，河南 平顶山 467000； 2.北京瑞赛长城航空测控技术有限公司，北京 100176)

煤矿安全生产监控系统已全面普及，实现了瓦斯气体浓度的实时监测和联网监控，及以公司为单位的煤矿安全环境监控参数的统一集中管理[1]。

但是安全监测系统由于受到环境、电磁干扰、设备故障、人为设备调校等因素的影响，出现大量异常高值数据，导致了大量瓦斯误报警。目前对于误报警采用的都是人工识别的方式。公司希望对甄别报警进行研究，实现对误报警的自动识别，提高识别效率，减少人工负担。

为了利用海量数据实现报警甄别，可借鉴目前研究较多的数据挖掘技术[2]。作为数据挖掘的重要研究课题之一，时间序列的数据挖掘与预测技术近几年发展迅速，它将数据挖掘和时间序列联系起来，支持解决发现新问题，以从海量的时间序列数据中挖掘出有价值的、潜在的、 未知的知识为目的[3-6]。

本文基于大数据的时间序列相关技术对瓦斯报警甄别进行了研究。

1 基于大数据的时间序列技术

瓦斯浓度每天的数据量达上万条，如果直接在原始时间序列上进行数据挖掘，不但效率低下，而且往往难以获得满意的结果。利用时间序列具有大数据的海量性和复杂性等数据特点进行研究。

1.1 时间序列的模式表示

时间序列的表示方法主要有频域表示法、奇异值表示法、符号表示法、分段线性表示法。

分段线性表示法不改变原序列的表示方式，具有更直观的形式，因此得到众多研究者的重视，是当前热门的模式表示方法[7-11]。

分段线性表示的时间序列模式：

L={(l1,k1),…,(li,ki)}

(1)

式中，li为第i(i=1,2,…,n)分段的长度；ki为第i分段的斜率。

在分段基础上，关键问题是相似性度量。

1.2 时间序列相似性度量

相似度量是通过被测模式和正常模式的相似性判断诊断出哪些是异常数据。相似性度量的方法有Minkowski距离、动态模式匹配距离及基于模式特征的K-近邻动态系统测量。

(1) Minkowski距离。

Minkowski距离作为相似性度量距离，是欧氏距离的推广，定义如下：

(2)

当p=2时，即为欧式距离。Minkowski距离应用于数据索引的相似性度量时具有简单直观、计算简便、可扩展性强等优点。然而也存在可靠性较差、对噪声及波动鲁棒性较差等缺点。

(2) 动态模式匹配距离。

与传统距离不同，动态模式匹配距离是通过模式进行匹配。降低了计算的数据量，提高了算法效率。

假定给定两个模式P1=(l1,k1)和P2=(l2,k2)，其中l和k分别表示模式的长度与斜率，则两个模式之间的距离为

(3)

式中，分母是将长度和斜率这两个不同的量纲进行统一，而取最小值则是为了能够突出短模式的重要性。

若有两个时间序列：

对应模式分别为

则两模式的动态模式匹配距离为

D(X,Y)=d(px1,py1)+min{D(P(X-1)，P(Y))，D(P(X),

P(Y-1))，D(P(X-1),P(Y-1))}

(4)

式中，d(px1,py1)为px1与py1之间的模式距离；P(X)-px1和P(Y)-py1分别为P(X)和P(Y)去除了第一个元素后的序列。

从上述公式可以看出，模式是由长度、斜率这两个特征表示。由于模式的长度与时间序列的振幅大小无关，而其斜率则体现了时间序列振幅的相对大小，所以动态模式匹配距离可以克服时间序列的振幅平移与伸缩变换。

1.3 基于模式特征的K-近邻动态系统测量

数据异常检测算法是利用不同特征间的距离不同进行分类[12-13]，选用前k个与待分类数据相似的数据，记录k个最相似数据中出现次数最多的类别为待分类数据的类别。

该检测方法检测步骤如下：

① 对已有报警类型进行数据建模，提取特征值。

② 对要检测的数据进行分段，利用式(3)计算距离。

③ 计算模式P的K-近邻可达距离。

该距离定义为

dist(q,p)=max(d(q,p),dk(p))

(5)

式(5)表示模式p与模式q的K-近邻可达距离，至少是模式p的K-近邻距离，或者等于模式p与模式q间的实际距离。离模式p最近的k个模式，模式p到这些模式的K-近邻可达距离都等于dk(p)。

④ 计算模式p的k局部可达密度。

该密度定义为

(6)

式中，Nk(p)为模式p的第k距离邻域，即p的K-近邻距离以内的所有模式，表示在模式向量集D中与模式p的距离不超过dk(p)的所有模式的集合。该值表示密度，密度越大，属于同一簇的可能性越大，密度越低，为离群模式的概率越高。如果模式p和周围邻域模式是相同簇，则可达距离为较小值dk(p)的可能性大，使得可达距离求和小，密度值高；如果p和相邻模式相距较远，可达距离可能需要较大的值d(q,p)，从而导致密度较小，并且更可能是离群模式。

⑤ 计算模式p的局部异常系数。

该系数定义为

(7)

LOF(p)值能够判断某模式异常可能性的大小：如果该值较大，则该模式的局部范围内比较稀疏，说明该模式是异常的可能性较大。

由于模式向量的数据量远小于原时间序列点数，因此会大大减小异常检测算法复杂性及计算时间。

2 基于大数据的报警模型建立

通过对近两年的瓦斯传感器报警数据的分析，同时征询煤矿安全技术专家意见，寻找出不同原因导致的报警特有的数据特征，建立初步的甄别数学模型。再结合基于模式特征的K-近邻检测算法，实现瓦斯报警类型的自动甄别。

安全监控系统中的瓦斯传感器报警分为以下3种类型。

2.1 瓦斯涌出报警模型

瓦斯涌出是指煤矿开采过程中，由受采动影响的煤层、岩层，以及由采落的煤、岩石向井下空间释放瓦斯的现象，分为以下两种情况。

(1) 一般连续不断、缓慢均匀涌出模型。

该情况的曲线如图1所示。

图1 一般瓦斯涌出数据曲线

此类瓦斯报警模型如下：

(8)

(2) 集中发生、涌出量不均匀的突出模型。

该情况的曲线如图2所示。

图2 瓦斯突出数据曲线

此类瓦斯报警模型如下：

(9)

注意，式(9)中的符号相同的各参数和其他公式中符号相同的各参数意义相同，但取值不同。

2.2 传感器调校导致的报警模型

传感器每星期需要进行调校，在进行高值调校时，需要先向传感器充入2%的甲烷气体，并持续90 s以上，这会造成瓦斯传感器在监控系统中超限报警。曲线如图3所示。

图3 传感器调校数据曲线

此类瓦斯报警模型如下：

(10)

调校规程要求持续90 s以上，除去采集间隔时间的影响，定为60 s。

2.3 干扰/故障模型

瓦斯传感器故障、供电异常、进水、接线松动、通信线路受电磁干扰等都会造成瓦斯数据报警的情况。主要有满量程和瞬间高值两种情况。

(1) 满量程故障模型。

满量程情况曲线如图4所示。

图4 满量程故障数据曲线

此类瓦斯报警模型如下：

(11)

(2) 瞬间高值模型。

瞬间高值情况曲线如图5所示。此类瓦斯报警模型如下：

(12)

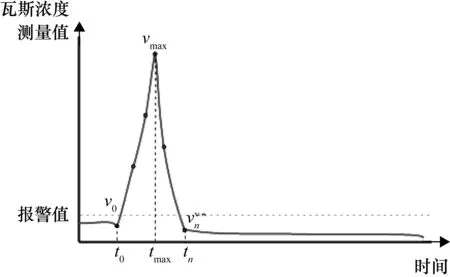
图5 传感器瞬间高值故障数据曲线

3 系统流程图及实验结果

利用软件程序实现系统流程如图6所示。

图6 瓦斯甄别判断流程

(1) 测试方法。

为了对系统软件功能及其效果进行考核，集中对2018年10月—12月三个月内的13075条瓦斯报警数据的甄别结果，由专业人员进行了详细的人工对比和鉴别，将鉴别结果录入数据库，通过查询语句分析统计结果。

(2) 测试结果。

① 在报警数据13075条中，程序甄别为瓦斯超限报警的927条，识别为传感器调校的10860条，识别为干扰/故障的1288条。

② 经人工鉴别，程序识别为瓦斯超限报警的927条记录中，实际为瓦斯超限的94条，其余属于将调校和故障信息误判为瓦斯超限信息；程序识别为传感器调校的10860条记录，经人工判断全部为调校；程序识别为干扰/故障的1288条记录中，有1127条为干扰/故障记录，其余为调校误判为干扰/故障。

③ 经统计，本程序识别正确的共计12081条，识别准确率达到92%。

4 结束语

本系统在平煤神马集团应用后，收到了很好的效果，对瓦斯报警类别的识别准确率达到90%以上，有效降低了瓦斯误报现象，同时对于真实的瓦斯报警能及时通知相关人员进行处理，有效地减少了相关人员的工作量，提高了工作效率。

系统存在的主要问题是甄别率还需要进一步提高，影响甄别率的因素主要有：

① 调校传感器时由于充气过程中出现间断，造成整个调校过程不连续，影响系统判断；

② 故障报警的情况多种多样，其数据规律不能完全用现有模型概括，需要引入更多的模型。

后续研究可以从算法入手，探索更有效的数据挖掘方法，降低干扰数据的影响，同时加强对传感器间关联关系的分析研究，排除不符合逻辑规律的报警，从而提高瓦斯甄别的准确率。