生物酶改良膨胀土的应力-应变关系

陈永青，文畅平，方炫强，陈宗辉，孙政，王解军

(1.中南林业科技大学土木工程学院，湖南长沙，410018；2.中南林业科技大学现代木结构工程材制造及应用技术湖南省工程实验室，湖南长沙，410018；3.湖南省交通规划勘察设计院，湖南长沙，410018)

在膨胀土地区进行工程建设，常用换土法、土性改良法、灰土桩法、水泥桩加固法以及控制含水率变化法进行地基处理。其中，改良法是一种环境友好型方法，不需要场地堆土，施工简便，成本较低，因此在工程中应用广泛。路基工程常采用石灰、水泥等无机材料对膨胀土进行改良[1]，相关规范[2-3]对石灰、水泥改良膨胀土作为路基填筑材料提出了要求。但采用石灰、水泥改良膨胀土也存在成本较高、拌合困难、对环境不友好的缺点。曾娟娟等[4-5]的研究表明，生物酶土壤固化剂(简称生物酶)能有效降低膨胀土的胀缩性，使其满足工程建设的要求。生物酶[6]为液态黏稠状，使用时将少量的生物酶与水混合稀释，即可达到工程相关标准[7-9]。生物酶容易拌合均匀，且无毒、无害、无腐蚀性，适用各种环境，是一种绿色环保的改良剂。目前，我国有关生物酶工程实践的报道较少。在路基工程实践中，均会针对膨胀土进行处理与处置，当对膨胀土进行改良后，其吸水膨胀、失水收缩的特性得到改善。膨胀土使用生物酶改良后仍然属于高塑性黏土[4-5]。而剑桥模型相关理论是应用最广泛的描述高塑性黏土的模型理论之一。在实践中，一旦采用改良法处理膨胀土，其工程用土即为改良后的人工重塑土。因此，对改良膨胀土的本构模型进行研究，具有较大的工程意义。原始剑桥模型是ROSCOE等[10-11]提出的适用于正常固结黏土与弱固结黏土的本构模型，称为Original Cam Clay 模型。该模型将流动规则、加工硬化规律和“帽子”屈服准则系统应用到模型中，开创了土力学的一个分支即临界状态土力学。随后，ROSCOE等[12]提出了椭圆形的屈服面轨迹，并在此基础上建立了Modified Cam Clay 模型，简称MCC 模型。剑桥模型能准确地描述土的静水压力屈服性、压硬性、剪缩性，该模型参数只有λ，κ和M，而且通过常规三轴试验就可以获取，这些特性使得剑桥模型得到了广泛的应用。同时，人们在该模型的基础上又进行了大量研究，并扩展了该模型的应用范围。魏汝龙[13-14]基于能量原理与正交流动法则，采用非固定的屈服面形状，使得固定屈服面的MCC 模型成为魏汝龙模型的一个特例。SANDLER等[15]对剑桥模型进行了修正，使其能够反映土的剪胀性、塑性硬化性。AMERASINGHE 等[16-18]将该模型的应用范围扩展到了超固结土。HSIEH等[19-21]在剑桥模型的基础上建立了考虑时间效应的修正模型。YIN等[22]采用剑桥模型模拟加速蠕变、加卸载特性。人们对剑桥模型的拓展都是以原始剑桥模型为理论框架，仍然是对临界状态土力学的丰富与发展。PRADHAN等[23]提出了扰动状态概念理论，以相对完整状态、完全调整状态、扰动度以及扰动函数为基本框架，描述“扰动”的演化过程。楚锡华等[24-28]基于该理论对粗粒土、结构性土、砂土及中粗砂进行了相关研究，并结合Duncan-Chang 模型进行描述。王金艳等[29-32]的研究表明，剑桥模型对描述黏性土软土的应力-应变关系的准确度比其他本构模型的高。而针对剑桥模型理论框架的改进是岩土本构模型的重要发展方向[29]。因此，本文作者基于剑桥类模型理论框架进行等向固结与回弹试验以及不同围压下的固结排水剪切试验，研究生物酶掺量对MCC模型相关参数λ，κ和M以及对魏汝龙模型相关参数的“扰动”作用，从而建立可对具有不同生物酶掺量的改良膨胀土进行描述的扰动修正MCC模型与扰动修正魏汝龙模型。

1 试验材料及方法

1.1 试验材料

膨胀土试验土样取自益娄高速公路K28+980 处，取土深度为2.0 m。新鲜土样呈现灰色、黄色、白色杂色，灰白色土样多以透镜体形式出现；土质细腻并有滑感，湿水时黏滑，干燥时坚硬。通过试验判定土样为中膨胀土。取土样进行相关物理力学特性试验，土样试验结果与文献[33]中的一致。

试验所用生物酶为泰然酶(TerraZyme)，为透明棕色液态复合酶制品。

生物酶掺量为掺加的固化剂质量与膨胀土干质量之比。本文分别取生物酶掺量为0%，1%，2%，3%和4%制作生物酶改良膨胀土土样。重型击实试验结果表明生物酶对改良膨胀土的最佳含水率影响不大，因此，制作土样的含水率均取18.0%，制备方法严格按照JTG E40—2007“公路土工试验规程”[34]进行。

1.2 试验方法

试验仪器为英国GDS-Instruments 公司生产的三轴试验系统。土样制作完成后随即放置于真空饱和器饱和，然后使用GDS 试验系统进行反压饱和，反压饱和有效压力为10 kPa。当孔隙水压力系数B≥0.95时，停止反压饱和。选择饱和固结模块与应力路径模块进行试验。为使试验更加精确，试验试样的制作土样仍然采用原土样制作，以保证试验土样只有生物酶掺入量为唯一变量，消除不同土样带来的误差。

1)利用GDS 系统中的饱和固结模块，将生物酶掺量分别为0%，1%，2%，3%和4%的试样进行各向等压固结回弹试验。不同生物酶掺量的土样均按照15 kPa/h的速度进行加载。试验结果表明，该加载速率能使孔隙水压力及时消散。不同生物酶掺量下的膨胀土均在400 kPa下卸载回弹，卸载速率为15 kPa/h。试验结果表明，该卸载速率可以使试样缓慢吸水膨胀。

2)选择应力路径试验模块，利用三轴试验系统对试样施加周围压力进行固结，控制为排水条件，施加轴向主应力，设置剪切速率为15 kPa/h。利用试验系统自带的GDS软件记录试验数据。

2 试验结果及分析

2.1 等向固结与回弹试验结果分析

1)当p较小时，膨胀土中的体积应变εv与p的关系呈现极小部分的直线段，说明土样的变形存在较小的弹性形变，随后εv-p呈现非线性的关系。

2)εv-lnp的关系大致呈现为一次函数关系，设等向固结部分直线的斜率为L，则εv=Llnp+εv0(其中εv0为体积应变曲线所对应的纵轴截距)。剑桥模型中的等向固结线斜率λ=(1+e0)L，等向固结线方程为e=e′-λlnp(其中e′为固结试验中e-lnp曲线的截距)。由于回弹试验部分εv-lnp也近似为直线关系，设该直线斜率为l，则剑桥模型参数回弹(膨胀线)斜率κ=-(1+e0)l，回弹试验结果如图1所示。由图1可以推导出卸载回弹试验段直线的表达式为e=ek-κlnp。

2.2 三轴固结排水剪切试验结果分析

三轴固结排水剪切试验结果见文献[33]。由三轴固结排水剪切试验结果可以看出：等向固结压力虽然有所不同，但当剪切破坏时，生物酶掺量增大，所需的偏应力更大，这说明生物酶可以增强其抗剪切破坏的能力。根据剪切试验结果可知：剪切破坏后的土样破坏特征也有所不同，膨胀土素土的剪切破坏面与最大主应力面的夹角约为60°；而随着生物酶掺量的增大，破坏形式呈现为不明显的鼓形。剪切破坏后土样如图2所示。

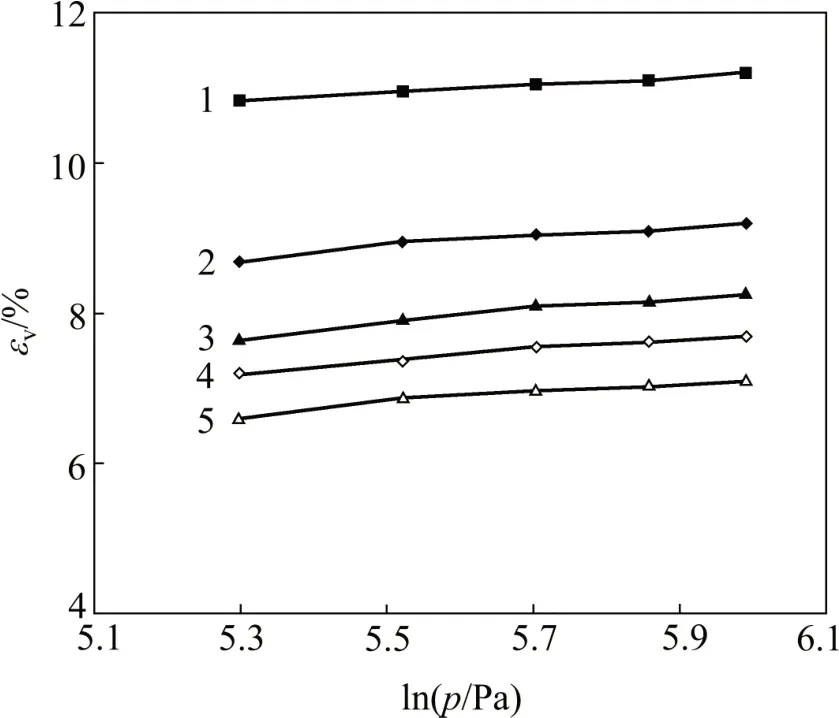
图1 卸载回弹试验εv-lnp曲线Fig.1 Curves of εv-ln p in unloading rebound tests

图2 剪切破坏后土样Fig.2 Soil samples after shear failure

在不同生物酶掺量下，取剪应变εs=15%时的偏应力q与球应力p为破坏点。破坏点的q-p关系如图3所示。由图3可知：q-p呈直线关系。设斜率为M，则该直线段的表达式为q=Mp+n。对不同生物酶掺量下q-p曲线的直线段进行拟合，拟合结果如图3所示。

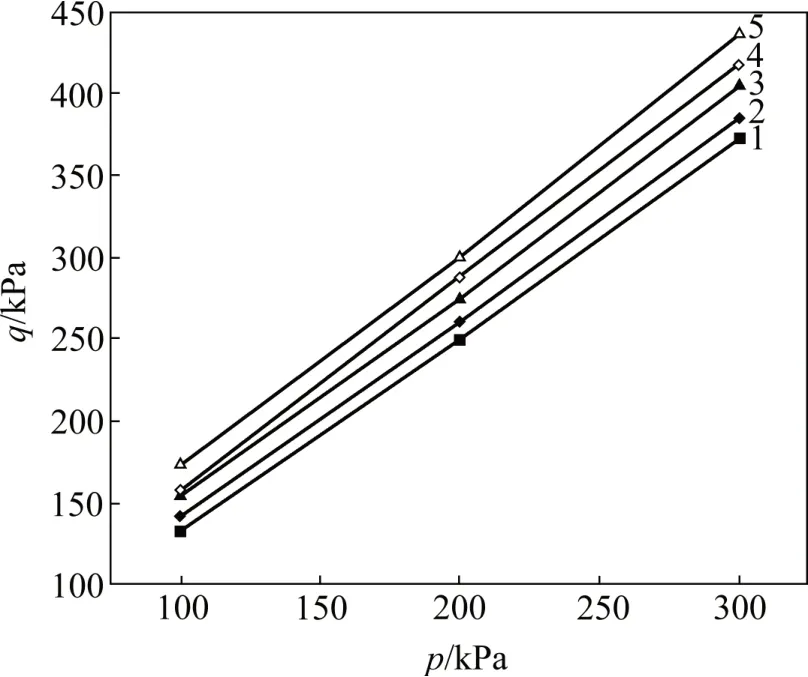
图3 破坏点的q-p关系Fig.3 Relationship of q-p at failure points

3 生物酶改良膨胀土的剑桥类模型框架

3.1 MCC模型框架

BURLAND[11]建立了一个新的能量方程，对剑桥模型进行了修正，建立了MCC 模型，该修正剑桥模型应用较为广泛。该模型参数λ，κ和M与初始剑桥模型中的物理意义一致。MCC模型的能量方程为

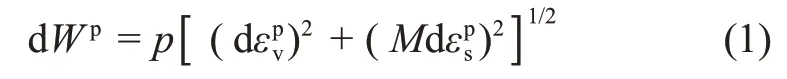
式中：Wp为塑性能，εpv为塑性体应变，εps为塑性剪应变。

按照原始剑桥模型求解屈服轨迹的方法，推导出MCC模型的屈服轨迹F为

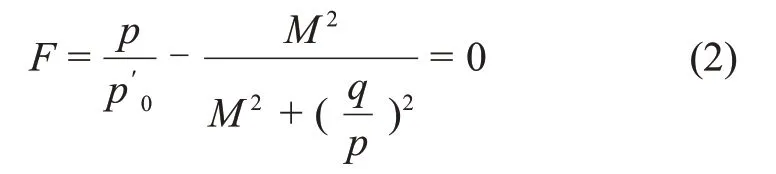
式中：p′0为屈服轨迹与p′轴交点的坐标值。

由式(2)可得：

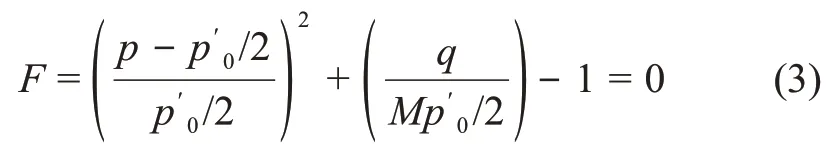
由式(3)可知屈服轨迹为椭圆，求解状态边界面方程：

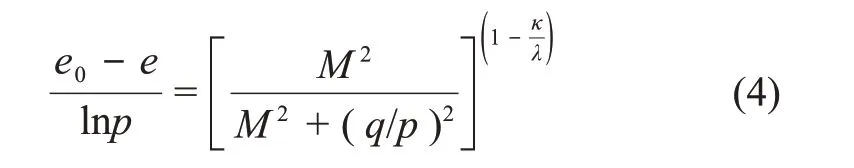
该模型的弹性应变增量方程为

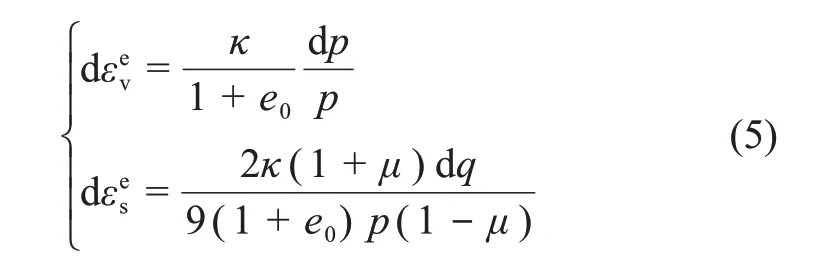
式中：εev为弹性体应变，εes为弹性剪应变；μ为泊松比。

修正剑桥模型的塑性应变增量方程如下：

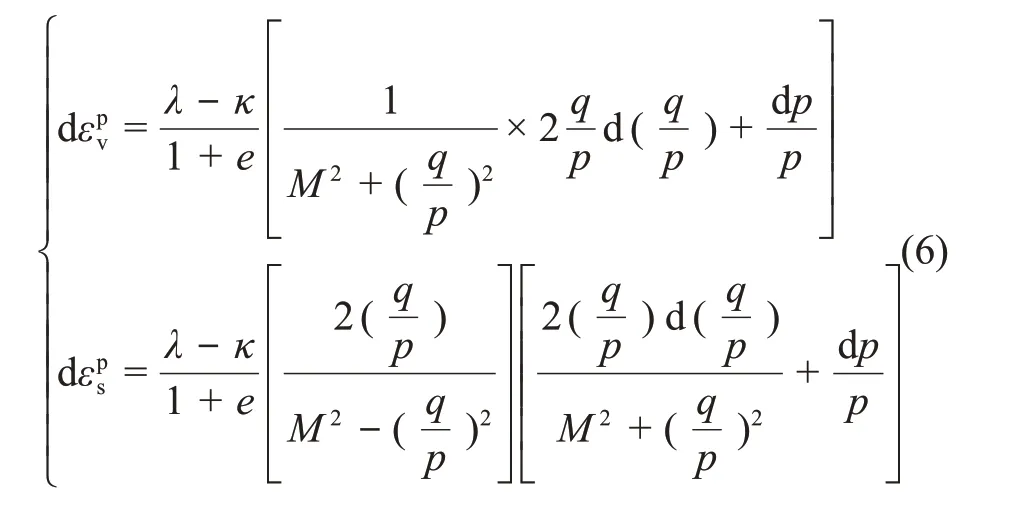
3.2 魏汝龙模型框架

魏汝龙模型[13-14]的能量方程与屈服面方程分别为：

式中：α，β和γ为魏汝龙模型中的形状修正系数；R为内能消散系数，其取值与α，β和γ有关。γ和R由屈服面图形确定。其中，α=1-γ，β=Mγ。由此可见，R，α，β和γ这4 个参数中只有1 个独立参量。当α=γ=1/2 时，魏汝龙模型的表达式为式(6)，此时魏汝龙模型退化为MCC 模型。因此，魏汝龙模型可充分考虑土体的受力情况，具有比MCC模型更强的适用性。魏汝龙模型的塑性体积应变增量方程为

式中：η=q/p。与MCC模型相比，魏汝龙模型的弹性理论框架为

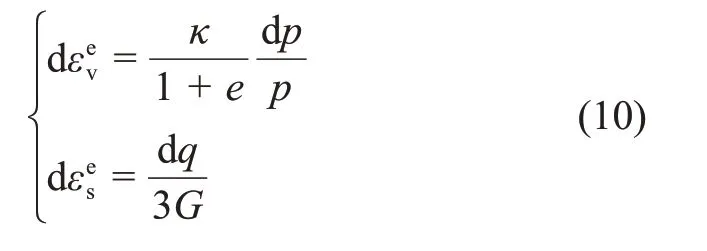
式中：G为剪切弹性模量。由式(10)可见，魏汝龙模型考虑了弹性剪应变，这也是其与原始剑桥模型以及MCC模型不同的地方。

4 生物酶改良膨胀土的模型参数分析

4.1 生物酶对参数λ与κ的影响

通过等向固结试验，将得到的数据整理为e=e′-λlnp；通过卸载回弹(膨胀)试验，将得到的数据整理为e=ek-κlnp，并进行1次函数关系的拟合，结果如表1所示。

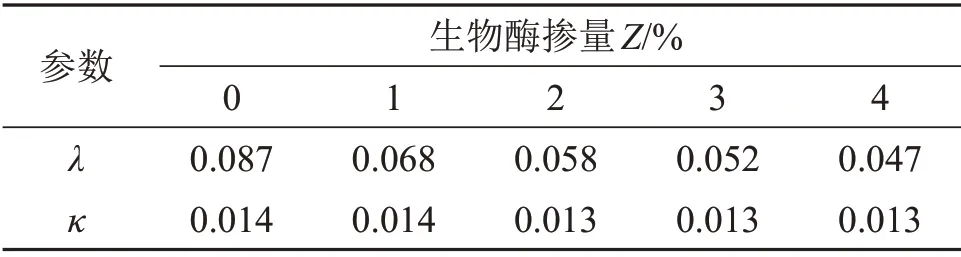
表1 参数λ与κ的拟合结果Table1 Fitting results of parameters λ and κ

由表1可知：固结线斜率λ对生物酶掺量Z敏感，而回弹膨胀线斜率κ与生物酶掺量Z相关性不大。将λ与生物酶掺量进行拟合可得：

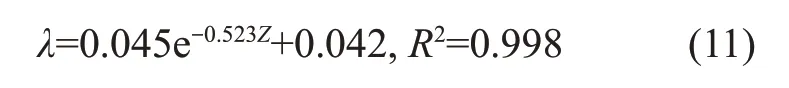
式中：回弹膨胀线斜率κ取为平均值0.013 4。正常固结线斜率λ、回弹膨胀线斜率κ反映了膨胀土抵抗压缩变形的能力，与硬化规律有关。从压缩试验曲线可以看出：正常固结线斜率λ变小，生物酶的掺入使得土体不易被压缩；而对回弹膨胀线斜率κ影响不明显。剑桥模型的弹性体应变增量表达式为dεev=可见生物酶改良膨胀土后，主要的弹性体应变变化不大，改良的效果主要体现在塑性变形部分。

4.2 生物酶对参数M的影响

根据固结排水剪切试验的破坏线方程q=Mp+n，对破坏线斜率M和破坏线截距n进行拟合，结果如表2所示。

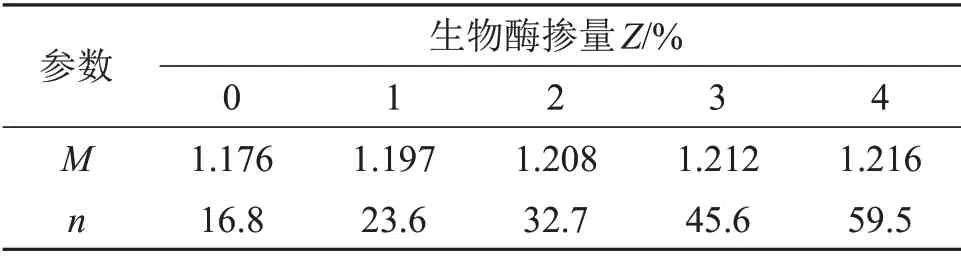
表2 参数M和n的拟合结果Table2 Fitting results of parameters M and n

由表2可知：破坏线斜率与生物酶掺量的相关性不强，可表示为一次函数关系；但随着生物酶掺量增大，破坏线截距显著提高。将破坏线斜率、截距与生物酶掺量进行拟合可得：

4.3 魏汝龙模型参数G的修正及生物酶对参数G和γ的影响

由式(10)可知魏汝龙模型考虑了弹性墙内加载的弹性剪应变，但杨林德等[35]的研究表明，在弹性墙内加载，塑性变形的比例也较大，特别是剪变形，不能忽略。修正剑桥模型因不考虑该部分剪应变，而魏汝龙模型考虑为弹性变形，因而与实际不符。NAYLOR[36]发现切线剪切模量Gt随球应力p增大而增大，但随偏应力q增大而减小。因此，本文对弹性墙内加载进行修正时，也考虑为非线性剪切模量，即通过可变的剪切弹性模量Gt考虑弹性墙内的塑性变形：

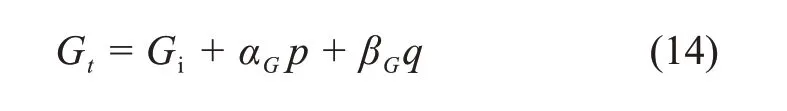
式中：Gi为初始弹性模量，αG和βG为试验常数。式(14)可转化为

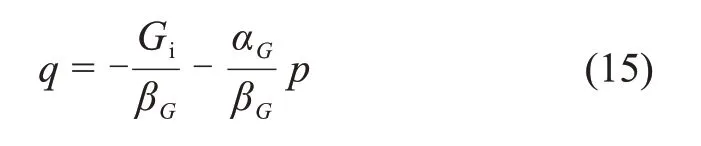
大量试验表明[37]，Gt与p和q的线性关系方程应在应力比为0.65～0.95 时建立，即应力水平应在屈服极限与破坏峰值之间。由q=Mp+n可得

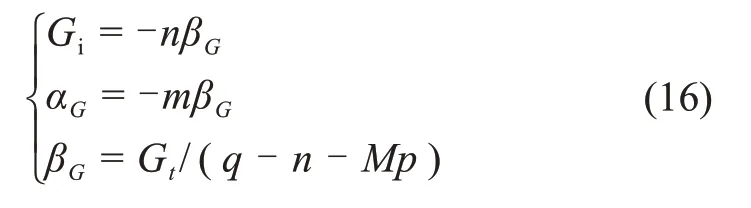
剪应变εs可表示为

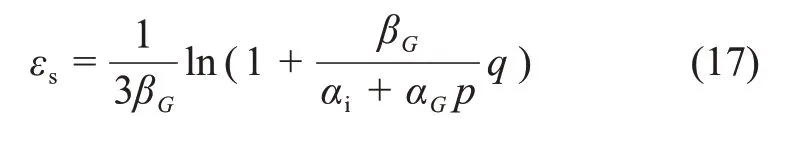
式中：αi为试验常数。

将式(16)代入式(17)可得

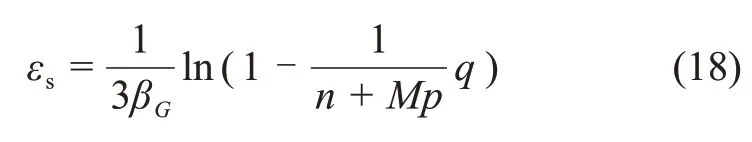
选取应力比为0.65～0.95时的q，由试验数据计算得到εs，将其代入式(18)可求得βG，将βG代入式(16)可解得αG与Gi。将不同生物酶掺量下的εs代入式(18)，即可得到不同生物酶掺量下的βG，αG与Gi。参数βG，αG与Gi的拟合结果如表3所示。

由表3可知：生物酶掺量Z对参数βG与αG影响不大，可表示为一次函数关系；但生物酶掺量对初始剪切弹性模量Gi影响较大，可表示为指数函数。

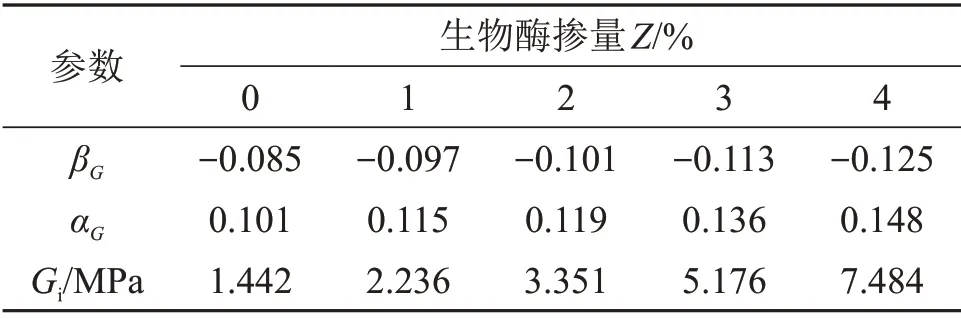
表3 参数βG，αG与Gi的拟合结果Table3 Fitting results of parameters βG,αG and Gi

由此可见，弹性墙内加载的塑性变形可通过非线性弹性理论进行计算，且与生物酶掺量有关。

魏汝龙模型考虑屈服面的形状参数，而黏土的有效应力与孔隙比之间存在唯一关系，与排水条件无关，即罗斯科面有唯一性，这与文献[38]中的结果一致。因此，三轴固结排水剪切试验只需要根据试验路径推算出路径不同阶段的孔隙比e的变化，将相同的孔隙比连接，绘制在p-q平面内e的等值线，从而得到屈服面形状[39]。将该屈服面形状参数γ与生物酶掺量Z进行拟合：

生物酶掺量对魏汝龙模型参数λ，κ和M的影响规律与MCC模型的一致。

5 基于扰动状态理论的修正MCC 模型与修正魏汝龙模型

5.1 统一的扰动函数

扰动状态理论通过扰动函数反映土的物理力学性质的持续变化过程，扰动函数首先需要确定一个参考状态，然后确定扰动度，即可对扰动因子处于任意状态进行描述。扰动函数的极限值一般为-1和1。负值表示土体物理力学性能因为扰动作用而增强。由于对膨胀土的生物酶改良均涉及到将生物酶与土体拌合均匀的过程，因此，将膨胀土素土考虑为相对完整状态，掺入生物酶改良的膨胀土考虑为调整状态。试验中只需改变生物酶掺量，其他试验条件保持不变，此时试验土样强度变形的不同可视为生物酶“扰动”所致。本文参考文献[24-27]，选择生物酶掺入量为扰动掺量，建立扰动度与生物酶掺量的函数关系。该扰动度物理意义明确且可进行精确计算。

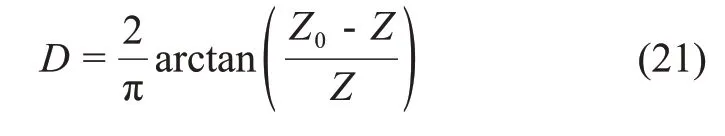
式中：(Z0-Z)/Z表示当前生物酶掺量Z相对于初始生物酶掺量Z0的变化值与当前生物酶掺量的比值。因此，式(21)又可以转化为

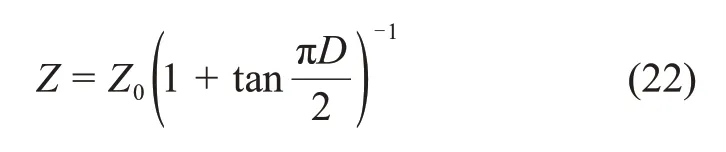
5.2 扰动理论修正MCC模型与扰动理论修正魏汝龙模型

根据掺入不同质量浓度生物酶的改良膨胀土试验结果可知MCC 模型与魏汝龙模型的相关参数发生了变化。将式(11)，(12)和(22)代入MCC模型(见式(5)和式(6))，则可得到扰动理论修正的MCC 模型；将式(11)，(12)，(19)，(20)和(22)代入式(9)和式(10)，则可得到扰动理论修正的魏汝龙模型。这2个修正模型均基于剑桥类模型框架，因而也采用增量表达，计算时需要进行积分处理。

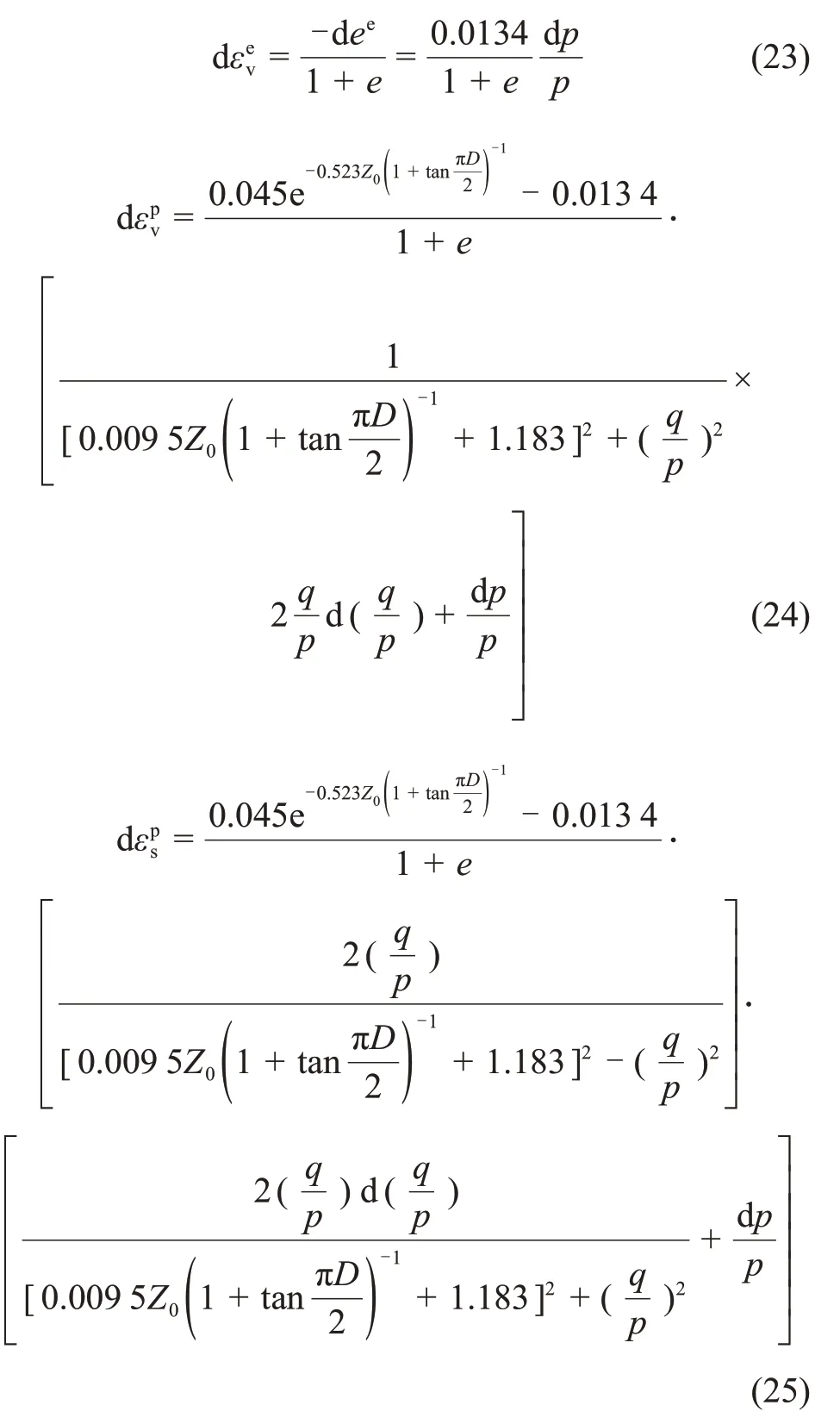
式(23)，(24)和(25)构造了扰动理论修正的MCC模型。

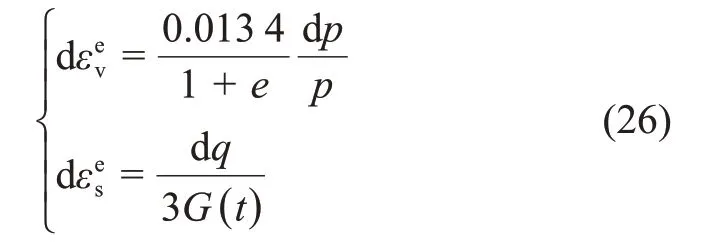
式中：

式中：

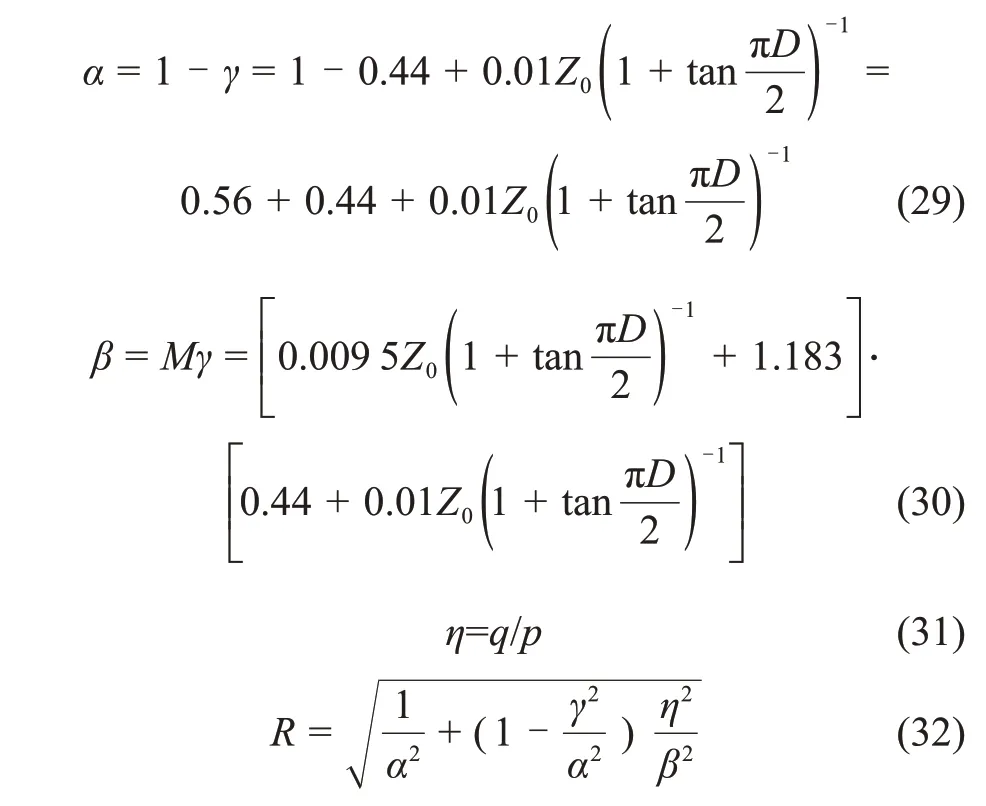
式(26)～(32)构成了扰动理论修正的魏汝龙模型。

5.3 模型预测与验证

5.3.1εv的预测验证

制作生物酶掺量为3.5%的土试样，按照本文方法进行试验。因本文建立模型时，生物酶掺量分别为0%，1%，2%，3%和4%，故通过MCC 模型、魏汝龙模型、扰动修正MCC 模型、扰动修正魏汝龙模型对生物酶掺量为3.5%的土试样的预测，可客观地对模型进行评价。其中，MCC 模型、魏汝龙模型的参数按照内插法取值，扰动改进MCC 模型、扰动改进魏汝龙模型参数采用扰动函数取值。对式(5)、式(6)、式(9)、式(10)、式(23)～(32)分别进行积分处理。计算中，将Z=3.5%代入，计算扰动度D，从而得到积分结果。不同模型中体应变预测值与试验值对比如图4所示。

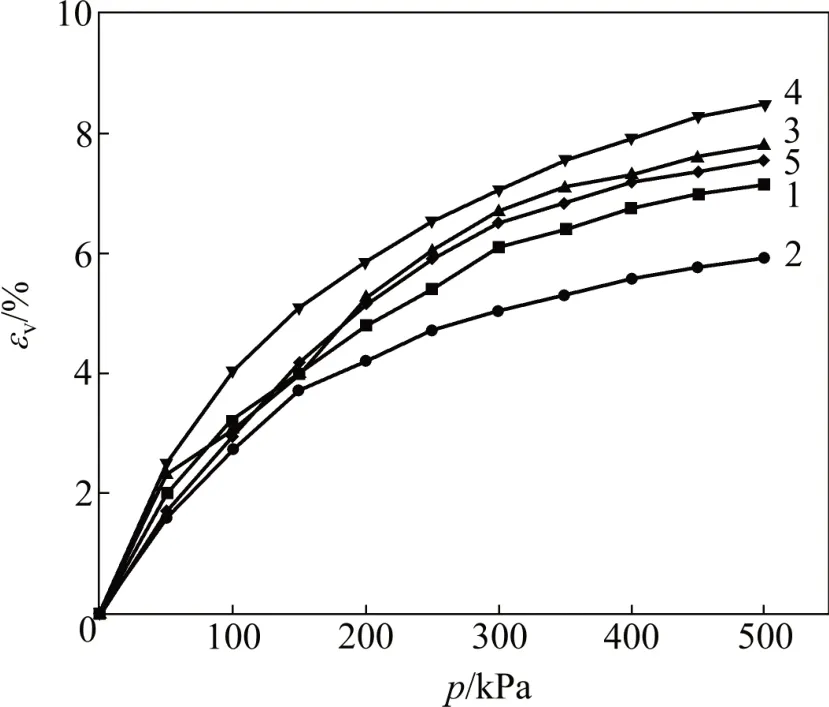
图4 不同模型中体应变预测值与试验值对比Fig.4 Comparison of predicted and experimental volumetric strains of different models

从图4可知：MCC 模型预测的体应变小于试验结果，且二者相差较大；而修正MCC 模型预测的体应变与试验结果较接近，魏汝龙模型预测的体应变大于试验结果，但二者相差幅度较小。由此可见，模型中应该考虑屈服面形状参数。张培森等[39]的研究也证明了魏汝龙模型中的形状参数对本构模型的影响。在对体应变的预测中，基于扰动理论修正魏汝龙模型预测结果与试验结果最吻合。而在MCC 模型中，由于屈服面形状是固定的，因此，不能正确反映生物酶掺量对其的影响，偏离程度最大。

5.3.2εs的预测验证

将试验土样重新碾碎，按照本文方法对其进行固结排水剪切试验，并对式(23)～(32)中的剪应变增量方程进行积分处理。不同模型中剪应变的预测值以及试验值对比如图5所示。

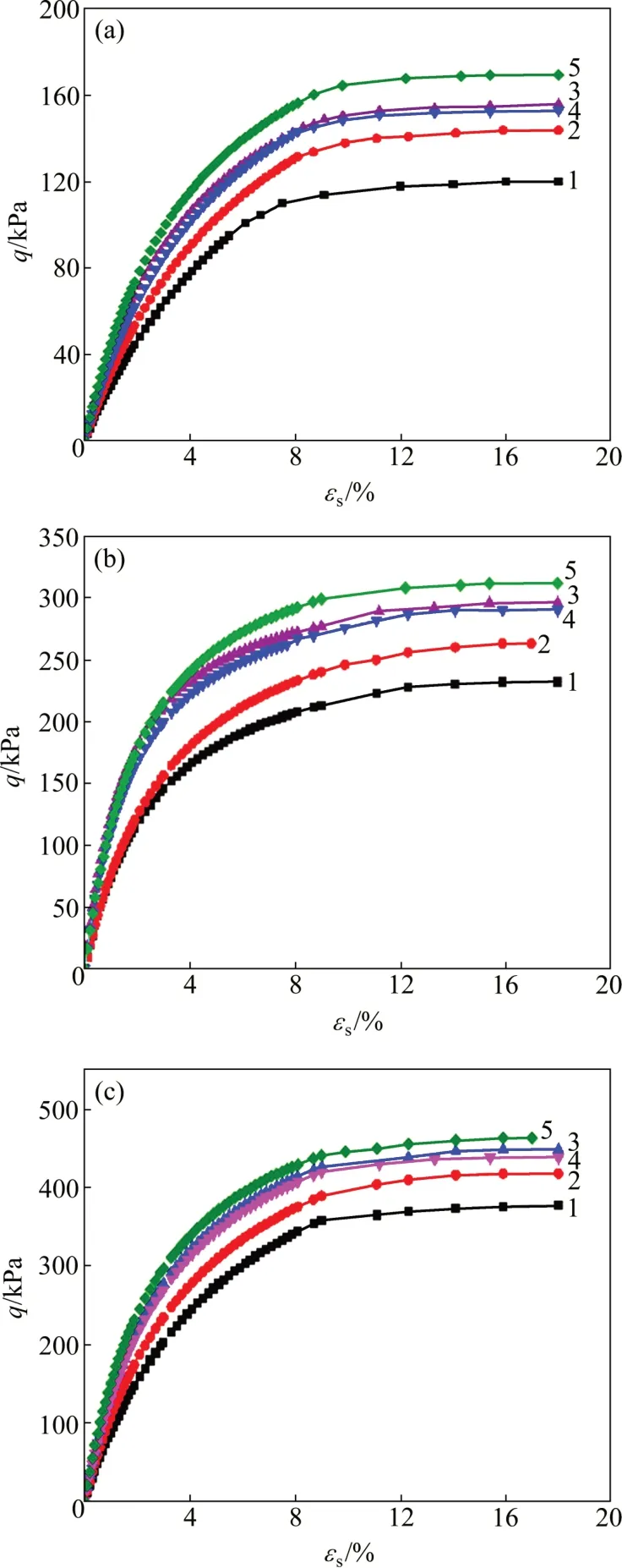
图5 不同模型中剪应变预测值与试验值对比Fig.5 Comparison of predicted and experimental shearing strains of different models

从图5可知：MCC 模型预测的剪应变小于试验结果，且相差较大；而扰动修正MCC 模型预测的剪应变与试验结果较接近，魏汝龙模型预测的剪应变大于试验结果，但相差幅度较小。在对剪应变的预测中，基于扰动理论的修正魏汝龙模型预测结果与试验结果最吻合，而扰动理论修正MCC 模型则可大幅改善MCC模型预测的准确程度。

6 结论

1)建立了相关参数λ(等向固结线斜率)、κ(回弹膨胀线斜率)、α(屈服面形状参数)、β(屈服面形状参数)、γ(屈服面形状参数)、M(破坏线斜率)、R(内能消散因子)与生物酶掺量的相关关系式；基于扰动理论提出相关参数的修正表达式，最终建立基于扰动理论的修正MCC模型以及修正的魏汝龙模型。

2)随着生物酶掺量的增大，等向固结线斜率λ显著减小；在同等三向固结力作用下，孔隙比变化减小，而回弹曲线斜率κ变化不明显；采用生物酶改良膨胀土后，主要的弹性体应变变化不大，改良的效果主要体现在塑性变形部分，生物酶改良膨胀土的抗压缩能力增强。

3)εv-p(体应变-球应力)与εs-p(剪应变-球应力)相关关系表现为应变硬化型，其硬化规律符合等向硬化与运动硬化理论，扰动理论修正的魏汝龙模型能更准确地描述试验结果。

4)MCC 模型对膨胀土体应变与剪应变的预测值与试验结果相差较大，但扰动理论改进的MCC 模型可大幅改善该模型预测的准确度，进一步证明扰动理论对模型修正的合理性。

5)基于扰动理论的修正MCC 模型、扰动修正魏汝龙模型与原模型参数的确定方法一致。由于生物酶掺量可精确控制，因此，本文模型的扰动函数取值也是精确的；本文引入的扰动函数是一个物理意义明确，取值方便的函数，故本文建立的基于扰动理论的修正模型能实现对任意生物酶掺量下的改良膨胀土应力-应变关系的描述。