含参的三角函数在定区间内的图像与性质

李云锦

[摘  要] 自2016年全国新课标理科Ⅰ卷第十二题的出现以来，各地开始相继出现含参的三角函数在定区间内的图像与性质问题的模拟题. 通過研究，我们可以发现此类问题的本质就是对三角函数的概念及三角函数四种表征（单调性、奇偶性、最值性、周期性）的理解与转化. 掌握此类问题，我们可以通过三角函数的上述四种性质有机地结合在一起，从而对整个三角函数有个全面的认识.

[关键词] 含参的三角函数;定区间;图像与性质

[?]学情分析

1. 学生的困惑之处

已知三角函数确定的解析式来研究三角函数的性质是学生很熟悉的问题，而“含参的三角函数在定区间内的图像与性质”这类问题是通过给出三角函数的性质来确定参数的取值范围或最值，两种问题相当于逆向思维. 前者是常规问题，学生能轻而易举地解决，后者对学生的逻辑推理能力、运算求解能力、直观想象能力要求相当高，而我们的学生这些能力较弱，导致此类问题很难解决.学生对三角函数各个性质单独研究比较容易，但是要把几种性质融合在一起看，这对学生能力要求是非常高的，导致此类问题很难突破.

2. 教学目标

逻辑推理能力、运算求解能力、直观想象能力是数学的三大核心素养，通过对此类问题的研究，意在提高学生的数学素养. 此类问题将三角函数的各个性质融合在一起，对此类问题的研究与解决，有助于学生站在更高的角度理解三角函数.

3. 解题方法解读及方法的可适性

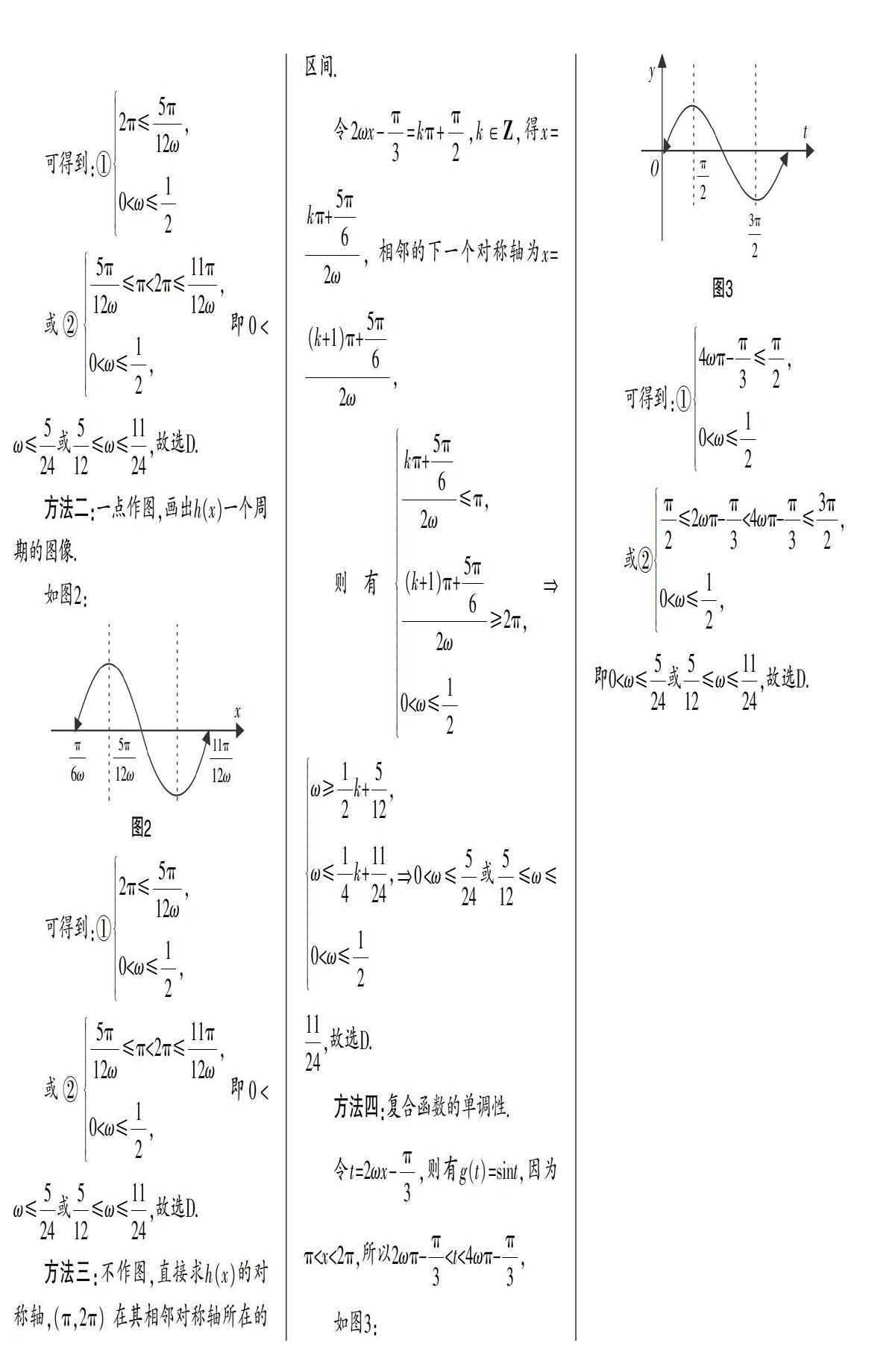
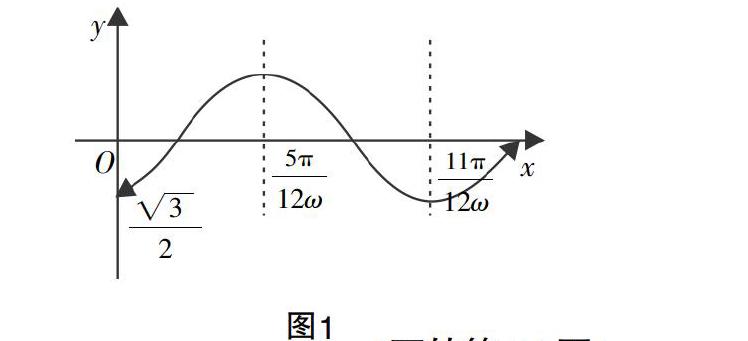
①方法一是通过图像的平移变换作出h（x）的图像;方法二是“一点”（“五点法”作图中的第一点）作图，画出h（x）一个周期的图像. 这两种方法都是利用数形结合的思想将三角函数的几何形态用图像表示出来，学生可以借助图像有较好的直观性. ②方法二的作图方法是方法一的改进，使得作图更加简便. ③方法三是利用整体思想直接求出三角函数的对称轴、零点. 一般情况下，对称轴和零点都含有参数. 再结合题目要求去求解参数的取值范围或最值. ④方法四是利用换元法把含参的解析式转化为熟悉的f（t）=sint，使得参数的位置从解析式转化到自变量t所给的区间，简化了试题的难度.

[?]问题辨析

例题：（2017年漳州市市质检理科第11题）已知函数f（x）=sin2ωx-2cos2ωx+1（ω>0）在定区间（π，2π）内没有极值点，则ω的取值范围为（  ）

方法三：不作图，直接求h（x）的对称轴，（π，2π）在其相邻对称轴所在的区间.

方法四：复合函数的单调性.

[?]教学启示

例题1展示了解决含参的三角函数在定区间内的图像与性质的通法，且利用了多种方法解决了此类问题，很好地启发和引导学生从不同的角度、不同的思路灵活地掌握知识的纵横联系，培养和发挥学生的创造性. 不仅充分调动学生思维的积极性，提高他们综合运用已学知识解答数学问题的技能技巧，而且也锻炼了学生思维的灵活性，这正是“智慧课堂”所倡导的. 如果教师能让学生会一题和通一类问题，那么学生在解决某一重难点问题时就会信心倍增.