不同轴压比下装配式再生混凝土剪力墙的滞回性能

张瀚天，袁朝庆，赵 艳，4*，肖 永，5，姜 静

(1.佳木斯大学建筑工程学院，黑龙江 佳木斯 154007；2.东北石油大学土木建筑工程学院，黑龙江 大庆 163318；3.黑龙江省防灾减灾及防护工程重点实验室，黑龙江 大庆 163318；4.中国地震局工程力学研究所与工程振动重点实验室，黑龙江 哈尔滨 150080；5.哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001)

如今，随着城市化进程的加快，我国劳动力成本上涨与能源紧缺等问题愈加严峻，天然骨料因过度开采而日益枯竭，城市中大量建筑物因已达到使用年限被拆除，从而产生大量的废弃混凝土；因此，装配式再生混凝土剪力墙结构因其具有良好的生态经济效益和社会效益而具有较高的推广应用价值[1]。目前，我国对该结构的研究相对较少，曹万林等[2-4]对半装配式再生混凝土剪力墙的抗震性能进行了研究与分析，研究结果表明：再生混凝土试件在低周反复荷载作用下的破坏形态和受力性能与普通混凝土试件相近，半装配式单排配筋再生混凝土剪力墙的综合抗震性能与现浇剪力墙接近。郭宏超等[5]对钢框架装配式再生混凝土墙结构进行了试验研究，研究结果表明：与纯钢框架结构相比，钢框架内配置再生混凝土墙板可显著提高结构的承载力和抗侧刚度，但是延性略有降低。为明确该种剪力墙结构在不同轴压比下的滞回性能，本文利用ABAQUS有限元软件对装配式再生混凝土剪力墙结构进行拟静力仿真模拟实验并进行系统性分析。

1 模型的建立与有限元验证

1.1 模型的建立

本文将文献[6]中的TW1剪力墙作为基础模型，建立有限元模型TW1*，尺寸和配筋与TW1剪力墙完全相同。试件由墙体、墙顶的加载梁以及墙底的地梁组成，墙体的尺寸为1 300 mm×200 mm×2 800 mm，地梁尺寸为2 400 mm×500 mm×500 mm，加载梁的尺寸为1 300 mm×250 mm×250 mm。地梁与墙体之间为套筒连接，套筒嵌入在墙体底部，墙体竖向钢筋伸入套筒100 mm，地梁竖向钢筋伸入套筒100 mm。有限元剪力墙模型中，混凝土采用C3D8R实体单元，钢筋采用TRUSS梁单元，套筒选用S4R壳单元进行建模。钢筋与混凝土之间的边界条件采用“Embedded”，该边界条件认为混凝土和钢筋在一起工作时无相对滑移。墙体与地梁之间的切向接触采用“摩擦”接触模型，法向接触采用“硬接触”。划分网格时采用六面体，大小为100 mm×100 mm×100 mm。有限元模型见图1。剪力墙整体结构下端固定，试件顶部按照设计轴压比施加轴向压力，在剪力墙结构上施加x方向位移循环荷载。为保证数值迭代的收敛性，本文采用位移控制加载，水平加载方式见图2。

(a)有限元模型 (b)网格划分

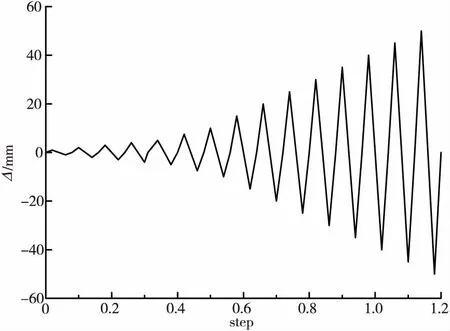
图2 水平加载方式

在本文中所有混凝土强度等级均为C40，普通混凝土的本构关系根据《混凝土结构设计规范》[7]所给出的混凝土受压应力-应变曲线计算得出。本文选用取代率100%的再生混凝土，其本构关系与普通混凝土类似，但是受压时的下降段与之相比更加陡峭，其受压段应力-应变曲线采用广西大学陈宗平等[8]给出的本构方程(如式(1)所示)，其中a=1.4，b=10，混凝土受压段应力-应变对比曲线见图3。再生混凝土受拉应力-应变曲线上升段的本构方程形式见式(2)，式中d的取值为1.26[9]，受拉时的下降段则采用普通混凝土受拉本构方程[10]。钢筋强度等级为HRB400级钢，为使模型在低周反复荷载下具有一定准确性，本文钢筋本构关系考虑了鲍辛格效应(Bauschinger effect)，采用随动强化(Bilinear Kinematic)模型[11]。

(1)

y=dx-(d-1)x6

(2)

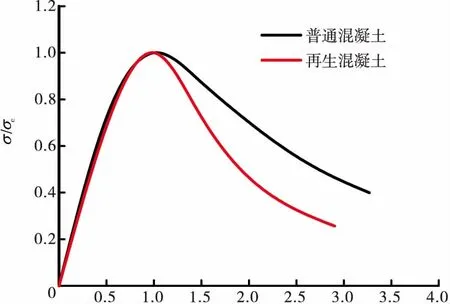
ε/εt

1.2 模拟结果验证

图4为TW1与TW1*的滞回曲线，图5为TW1与TW1*骨架曲线的对比。采用“等能量法”近似确定试件的特征值。模拟与实验的对比结果置于表1，其中Fy、Fm和Fu分别表示屈服荷载、峰值荷载和破坏荷载。

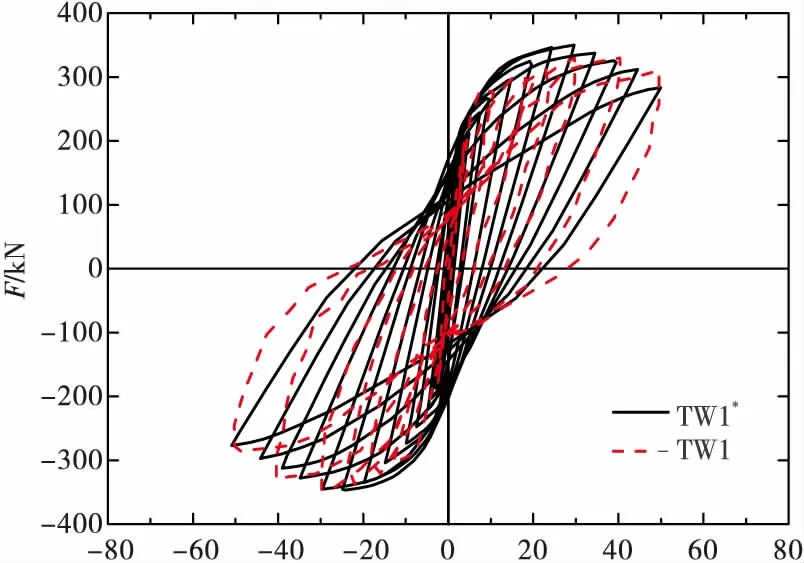
Δ/mm

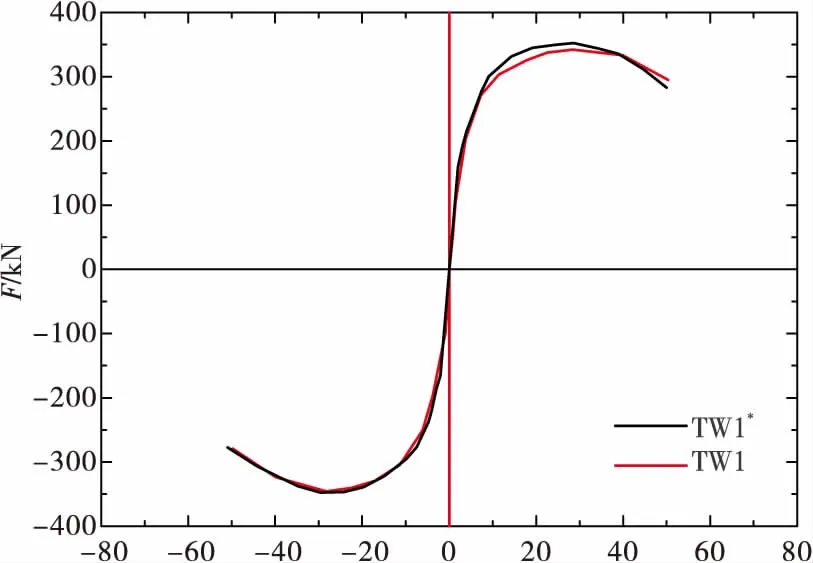
Δ/mm

由图4、图5与表1可知，有限元与试验两者的水平力-位移曲线的形状相似，走向趋势大致相同，各级循环的峰值点相差不大，有限元模拟的屈服位移先于试验出现，峰值阶段的水平承载力要略大于试验值，平均误差均在10%以内。产生误差的原因主要有以下2个方面：1)在有限元中剪力墙底梁完全固定，而试验时剪力墙的底部约束不能达到理想状态，易产生滑移，导致有限元剪力墙模型的自由度小于试验试件的自由度；2)在试验过程中，混凝土会因为开裂或剥落而退出工作，但是在有限元模拟时，混凝土主要考虑的是材料的损伤，单元并不是完全失效，在加载的中后期也能发挥一定的作用。总体来看，用ABAQUS分析所得的滞回曲线、骨架曲线比较符合实际，虽然存在一定误差，但是这样的精确度已经可以满足工程上的实际应用，能够很好地反应剪力墙在低周反复荷载下的滞回性能；因此，利用ABAQUS软件来模拟装配式再生混凝土剪力墙是合理可行的。

2 不同轴压比下装配式再生混凝土剪力墙的滞回性能

为研究不同轴压比下装配式再生混凝土剪力墙的滞回性能，本节在TW1*剪力墙模型的基础上，将普通混凝土的本构关系换成再生混凝土的本构关系，通过增加剪力墙的轴向压力改变轴压比，各剪力墙模型的轴压比分别为0.1、0.2、0.3、0.4和0.5，为方便对比分析，模型命名为ACR-X剪力墙，X代表该剪力墙的轴压比。

表1 试验结果与有限元结果对比

2.1 水平力-位移曲线

图6为不同轴压比的装配式再生混凝土剪力墙滞回曲线，图7为不同轴压比的装配式再生混凝土剪力墙骨架曲线。

Δ/mm Δ/mm Δ/mm

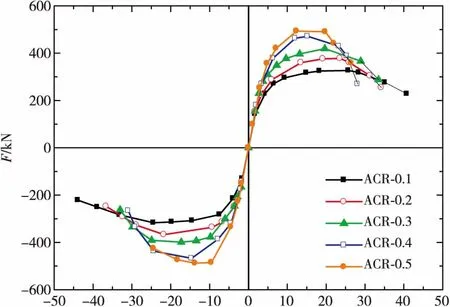
Δ/mm

由图6和图7可知，不同轴压比剪力墙的滞回曲线光滑，正反两个方向基本对称。初始加载时，各剪力墙均处于弹性阶段，滞回曲线均呈直线状，卸载后剪力墙基本能回到原位，滞回环面积较小；随着推覆位移的增大，剪力墙进入塑性阶段，曲线开始出现弯曲，卸载后剪力墙有一定的残余变形，滞回环面积不断增大；当位移继续增大时，剪力墙所承受水平力达到峰值阶段，随后各剪力墙的承载力开始下降直至破坏。ACR系列各剪力墙的骨架曲线正反两个方向基本对称，具有完整的上升段及下降段，不同轴压比的装配式再生混凝土剪力墙的骨架曲线有所不同。在弹性阶段时，轴压比越大的剪力墙斜率越大，说明随着轴压比的提高，剪力墙的初始刚度也随之提高；当推覆位移逐渐增大，剪力墙进入屈服阶段，屈服后承载力缓慢上升达到峰值，在此阶段的同等位移条件下，剪力墙的水平承载力随着轴压比的提高而增大，但是剪力墙的峰值位移也随着轴压比的提高而降低，说明轴压比越高，剪力墙脆性越显著[12]；当位移持续增大时，轴压比越大的剪力墙骨架曲线越短，破坏位移出现要早于轴压比小的剪力墙，并且骨架曲线的下降段也越陡峭，这说明了轴压比大的剪力墙承载力退化速度更快，延性也越差。

2.2 承载能力

将不同轴压比的装配式再生混凝土剪力墙不同状态时所对应的水平承载力置于表2。表2中的Fy、Fm和Fu分别表示屈服荷载、峰值荷载和破坏荷载，图8为水平承载力与轴压比关系。

表2 ACR系列剪力墙不同阶段时的水平承载力 kN

图8 水平承载力-轴压比关系图

由表2和图8可知：轴压比对装配式再生混凝土剪力墙的水平承载力影响较大，随着轴压比的提高，剪力墙的屈服荷载和峰值荷载均有所增加。与ACR-0.1剪力墙相比，当轴压比每增加0.1时，屈服荷载约提高了13.8%、峰值荷载大约提高15.7%；当轴压比在0.1～0.4范围内变化时，水平承载力增加的速率呈线性上升；当轴压比超过0.4时，水平承载力增加，但增加趋势有所放缓。

2.3 变形与延性

将不同轴压比的剪力墙位移特征值及延性系数置于表3中。表3中，Δy为屈服点所对应的位移；θy为屈服点所对应的层间位移角；Δu为破坏点所对应的位移；θu为破坏点所对应的层间位移角；μ为延性系数。

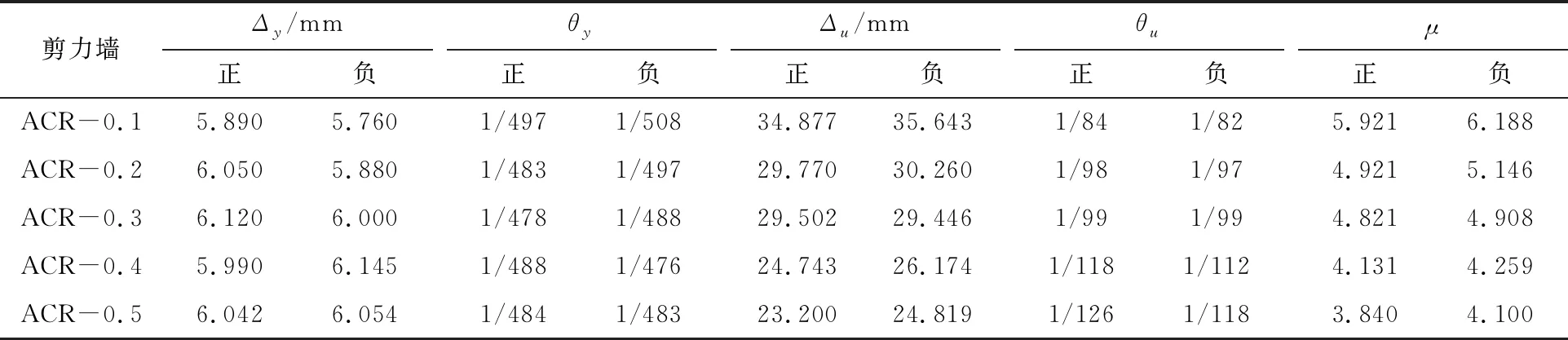
表3 ACR系列剪力墙位移特征值和延性系数

由表3可知，轴压比对剪力墙的变形与延性有很大影响。随着轴压比的提高，剪力墙的破坏位移与延性均有所降低，但是屈服点位移变化不大。与ACR-0.1剪力墙相比，当轴压比提高一倍时，剪力墙的破坏位移降低了14.9%，延性下降了16.8%；当剪力墙的轴压比提高到0.3时，破坏位移降低了16.4%，延性下降了19.7%；当剪力墙的轴压比达到0.4时，破坏位移降低了27.8%，延性下降了30.7%；当轴压比提高到0.5时，破坏位移降低了33.5%，延性下降了35.1%。此外，剪力墙破坏点的层间位移角随着轴压比的增加而减小，最小破坏点层间位移角出现在ACR-0.5剪力墙的正向，最小值为1/126，小于规范中要求的弹塑性位移角限值1/120。然而，ACR-0.4剪力墙的最小破坏点层间位移角为1/118，仅仅高出限值的1.7%，处于危险边缘。因此，在设计装配式再生混凝土剪力墙结构时，轴压比不宜超过0.4。

2.4 刚度退化

不同轴压比的装配式再生混凝土剪力墙各阶段的割线刚度见表4，表中Ky、Km和Ku分别表示屈服点割线刚度、峰值点割线刚度和破坏点割线刚度，刚度退化曲线见图9。

由表4与图9可知，轴压比对剪力墙的刚度影响较大，随着轴压比的提高，剪力墙各个阶段的割线刚度均有所增加。剪力墙在破坏前的相同位移条件下，轴压比越大，剪力墙的刚度越大，说明轴压比越大剪力墙抵抗变形的能力要更强一些。原因是轴向压力的增大限制了混凝土受拉裂缝的发展。不同轴压比的剪力墙刚度退化趋势大致相同，均随着位移的增加而刚度减小。屈服前，剪力墙的刚度退化速度较快，并且可以看出轴压比低的剪力墙刚度退化速度越快。屈服后，剪力墙的刚度退化速度较之前相比相对缓慢。当剪力墙水平承载力下降到峰值荷载的85%后，各剪力墙刚度退化速度出现反转，轴压比高的剪力墙刚度退化速度越快，原因是轴压比越大，剪力墙延性不足，达到破坏荷载后剪力墙的刚度迅速下降。

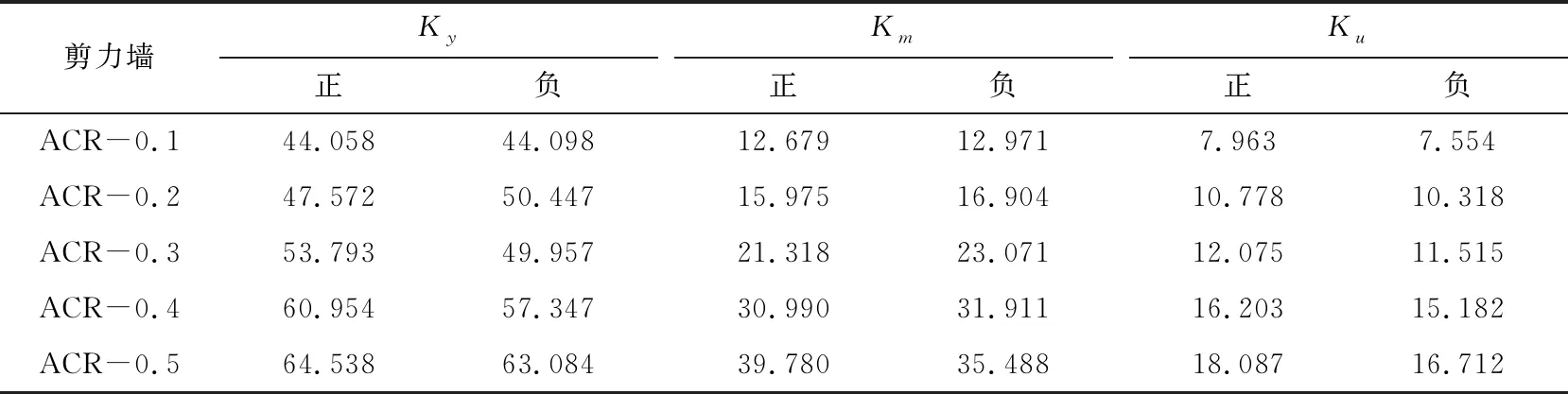
表4 ACR系列剪力墙割线刚度 kN·mm-1

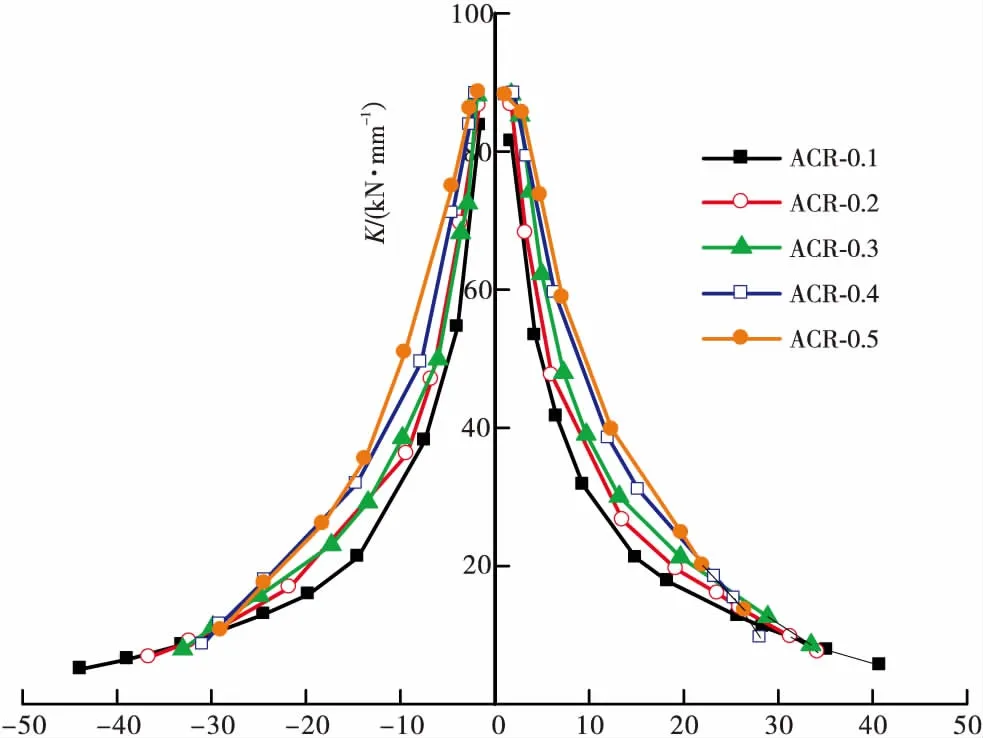
Δ/mm

2.5 耗能能力

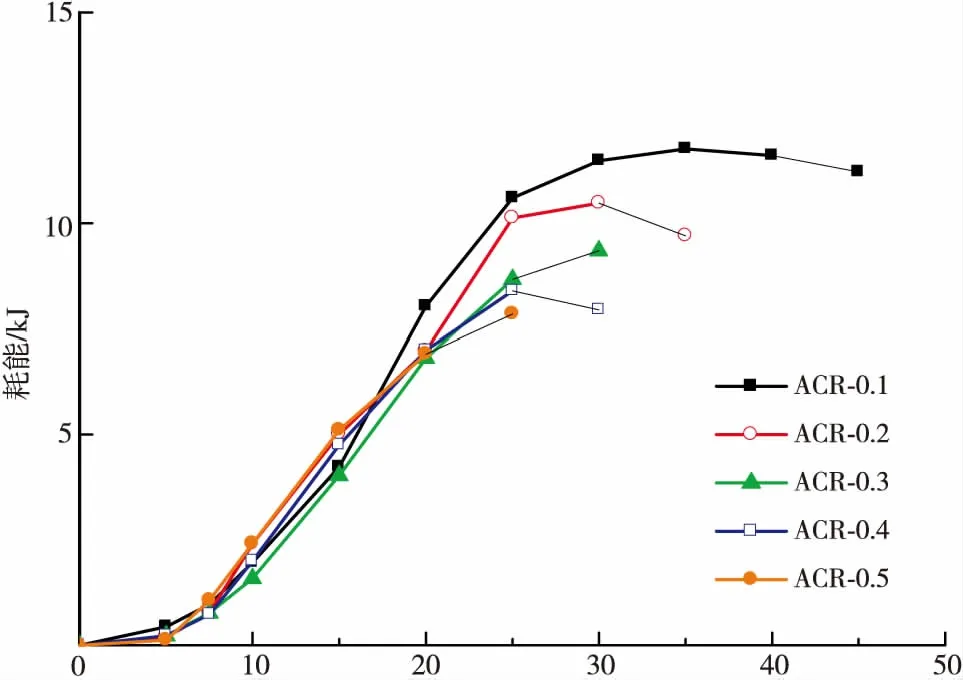
剪力墙的耗能能力是评价结构滞回性能的一个重要指标，它是指剪力墙在受力的过程中吸收能量的能力。耗能能力可通过滞回环的面积来衡量，滞回环的面积越大说明耗能能力越高，耗能的单位为焦耳。不同轴压比的装配式再生混凝土剪力墙耗能与位移关系见图10。

由图10可知，不同轴压比的剪力墙耗能曲线在初始阶段时基本重合，上升速度较快；达到峰值位移后，耗能曲线趋于稳定，轴压比越小，剪力墙的单圈滞回面积越大，耗散能量越多；在加载后期，剪力墙的滞回面积随着轴压比的增加而减小，轴压比越大的剪力墙耗能能力明显降低，脆性也愈加显著。

3 结论

1)轴压比对装配式再生混凝土剪力墙的水平承载力影响较大，随着轴压比的提高，剪力墙的屈服荷载和峰值荷载均有所增加，轴压比每增加0.1，屈服荷载大约提高13.2%、峰值荷载大约提高15.3%。

Δ/mm

2) 随着轴压比的提高，剪力墙的耗能能力与延性均有所下降，轴压比每增加0.1，延性系数大约下降10%。

3)剪力墙在破坏前的相同位移条件下，轴压比越大，剪力墙的刚度越大；轴压比越小，剪力墙刚度退化速度越快；当剪力墙水平承载力下降到峰值荷载的85%后，各剪力墙刚度退化速度出现反转。

4)在实际工程中设计装配式再生混凝土剪力墙结构时，应严格控制轴压比，尽量选用轻型楼盖以降低组合剪力墙的轴压比。轴压比不宜超过0.4，通过合理的设计可将该结构应用于小高层建筑当中。