基于电力数据与机器学习的家庭收入估计方法

关键雄

(1.西南交通大学电气工程学院，四川 成都 611756；2.新加坡淡马锡理工学院清洁能源中心，新加坡 529757；3.新加坡国立大学计算机学院，新加坡 117417)

0 引 言

在整个电网体系当中，用户群体是关键一环。智能电表的普及能够越来越容易地获得每个家庭的用电量数据。通过对电表数据的监测，有关部门可以实现对用电高峰的调度，还可以进行对用电器的故障检测[1]。在大数据的时代背景下，监测家庭用户的电力负荷，并将电力数据与生活中一些看似不相关的信息综合起来，便能得到很多意想不到却又很具有价值的信息[2]。这些信息将会带给诸如电力公司、经销商等多个行业人群有利的信息，从而帮助人们的生活变得更加便捷。

当前的研究工作已经提出总的家庭用电量数据能够被用来评估一些家庭的静态特性，比如房屋面积、居住人口等[3]。这些特性信息不仅能够用于目标能源反馈，而且可以帮助调整家庭中恒温器的温度设置，从而提高能源效率和用户的舒适度，另外还能用于目标能源查询[4]。Nipun Batra等人[4]使用无监督的能量分解方法预测6个静态房屋属性，分别为房屋的年龄、房屋面积、家庭收入、楼层数、房间数、居住人口。从总的用电量数据中分解出暖通空调的功率信号，比起简单地使用总的用电量数据，能够使评估房屋静态特性的准确率提高10%。

为了提高非侵入式负荷监测的准确率，还可以通过数据融合的方法来进行，即除了电力数据之外，添加一些情境性信息，例如家庭中用电器的物理位置等。Akshay等人[5]利用通过无线位置传感器获得的用户实时位置信息和用电器的用电量数据，来提高现有的非侵入式负荷监测方法的准确率。

下面提出将总的用电量信息和静态的房屋面积信息综合起来，用来推断一个家庭的收入情况，帮助相关企业部门和经销商对消费群体进行准确的定位和把控，使商家更有针对性地为用户提供需要的服务和产品，实现对于商业发展的促进，让人们能够享受大数据时代带给生活的便利。此外，国家和政府可以通过这个技术，对一个小区甚至一个地区进行粗略但成本很低的统计，从而帮助政府更好地了解居民的收入，进而采取一系列管理和政策上的调整。

由于简单地使用从智能电表读取的用电量信息对家庭收入进行估计的准确率不高，除了对总的用电量进行能量分解来提高准确率，也可以采用增加附加信息的数据融合方法，下面采用的便是后者的研究思路。由于房屋面积信息作为房屋的一个最为明显的静态特性是非常容易获得的，因此将总的用电量信息和静态的房屋面积信息综合起来推断家庭收入情况。经过研究发现，增加了房屋面积这一信息之后，对家庭收入情况估计的准确率有了很大的提高。

1 数据准备与特征提取

1.1 数据准备

主要使用公开可用的数据集Dataport中的数据来进行对家庭收入的估计。Dataport数据集是由Pecan Street公司创建的，包含从2012—2014年700多个家庭每秒钟的总用电量数据，同时也包含了一部分家庭的基本信息调查数据[6]。从Dataport数据集中提取出元数据表、3年的家庭用电量数据表和对应3年的家庭情况调查表，然后从这3组数据表中提取整合出对应样本家庭该年的总用电量情况、房屋面积以及收入情况3部分信息，最终得到可用的样本家庭数据371个。为了方便评估每个家庭收入，将家庭收入情况划分为两个类别，分别为年收入低于10万美元和年收入等于或者高于10万美元[7]。

1.2 特征提取

从收集到的家庭总用电量信息中，提取出该年中家庭总用电量的平均值(mean use)、中位数(median use)、最大值(max use)、极差(range use)、标准差(std use)以及该年中每小时的家庭总用电量超过2 kW的时数(count more 2)、超过4 kW的时数(count more 4)、超过6 kW的时数(count more 6)、超过8 kW的时数(count more 8)、超过10 kW的时数(count more 10)、超过12 kW的时数(count more 12)、超过16 kW的时数(count more 16)、超过18 kW的时数(count more 18)，总共13个电力特征[8-9]。另外，将房屋面积(total square footage)作为新增加的特征，和这些电力特征一起构成14维的特征数据集。

图1和图2分别随机选取了两组不同的二维特征，通过散点图的形式展示了数据集中各个样本家庭的部分特征分布情况以及这些样本家庭的年收入所属类别。在图1中，横、纵坐标分别选取的特征是房屋面积和该年中家庭总用电量的平均值，圆圈代表该样本家庭的年收入低于10万美元，五角星代表该样本家庭的年收入等于或者高于10万美元。在图2中，横、纵坐标分别选取的特征是该年中家庭总用电量的标准差和最大值，三角形代表该样本家庭的年收入低于10万美元，正方形代表该样本家庭的年收入等于或者高于10万美元。从两图中的数据点分布来看，数据并非线性可分的，因此无法简单地利用线性超平面将两个类别区分开。

图1 房屋面积与平均用电量二维特征数据分布散点

图2 用电量标准差与最大用电量二维特征数据分布散点

2 实验设计与步骤

2.1 分类算法的选择

对家庭收入的估计属于机器学习的分类问题。最常见的几种机器学习分类算法有逻辑斯蒂回归(logistic regression)、支持向量机(support vector machine, SVM)、决策树(decision tree)、随机森林(random forests)、K-近邻(K-nearest neighbor classifier, KNN)等[10]。

其中，K-近邻算法又称为一种懒惰学习算法，它通过测量不同特征值之间的距离来对目标对象进行分类[11]。KNN算法步骤如下：

1)确定k的大小和距离度量；

2)对于测试集中的一个样本，找到训练集中和它最近的k个样本。

KNN是基于内存的方法，其优点是一旦训练集增加了新数据，模型能立刻改变。但是分类时的最坏计算复杂度随着训练集增大而增加，除非特征维度非常低。此外，需要一直保存着训练集，不像参数模型训练好模型后，可以丢弃训练集。

SVM的主要思想就是找到空间中存在的一个能够将所有数据样本区分开的超平面，并且使得得到的样本数据到这个超平面的距离最短。SVM能解决线性和非线性问题，因此可以分为线性和非线性两大类[12]。

线性SVM(linear SVM)在解决现实的分类问题时，通常与线性逻辑回归的效果近似，对于线性可分的类别数据性能良好。

核SVM(kernel SVM)是指在 SVM 中引入核方法，使SVM 变为非线性分类器，从而解决线性不可分数据。常用的核函数一般称为高斯核，通常简写为

k(x(i),x(j))=e(-γ‖x(i)-x(j)‖2)

式中：γ为一个要优化的自由参数，可以被理解为高斯球面的阶段参数，若增大γ的值，会产生更加柔软的决策界；k为两个样本间的相似形函数；x(i)、x(j)为两个样本。高斯核中e的指数范围小于等于0,因此高斯核值域范围为(0,1]，特别地，当两个样本完全一样时，值为1；两个样本完全不同时，值为0[10]。

决策树的生成是一个递归过程，训练决策树模型时，从根节点出发，使用信息增益最大的特征对数据进行分割，然后迭代此过程[13]。决策树会将特征空间分割为矩形，因此其决策界很复杂。熵和基尼系数是决策树常用的两个度量，而且两者的结果相似，选择任何一个都是可以的。决策树直观，便于理解，具有很好的模型可解释性，对于小规模数据集很有效；但类别较多时，错误增加较快，可规模性不强。很多棵决策树集成，就叫做随机森林。

从前面可以得知，用于所研究的特征数据集并非简单的线性可分数据，因此线性逻辑回归和线性SVM 两种算法适用性不强。而这里的数据特征维度并不低，运用KNN算法分类时的最坏计算复杂度和预测时的计算成本相对较高。相对来说，从各种分类算法本身的优缺点出发，拟采用决策树和核SVM两种算法来对样本家庭的年收入情况进行分类估计。同时，将线性SVM和KNN作为基准算法，与决策树和核SVM的分类效果进行对比，从而验证算法选择的合理性。

Python的scikit-learn是一个专门的机器学习算法库，它提供了执行机器学习算法的模块化方案。以上这几种分类算法的模型都可以从scikit-learn中直接调用，简洁和高效。

2.2 估计家庭收入的步骤

2.2.1 仅通过家庭总用电量数据估计家庭年收入

步骤1：只选取13个维度的电力特征组成数据样本X，将样本家庭的年收入类别作为要预测的目标y。

步骤2：为了评估训练好的模型对新数据的预测能力，先将数据集(X,y)随机分为两部分: 训练集占80%,测试集占20%。

步骤3：对训练集中每一维度的特征计算出样本平均值和标准差，进而对数据集进行标准化，使每一维度特征的重要性等同。

步骤4：调用KNN、线性SVM、决策树以及核SVM4种不同的分类器训练模型。针对每一种分类器，分别设置合适的模型参数和随机参数。

步骤5：分别计算每个模型在测试集上的分类准确率，以此来对比和评价以上4种模型的性能。

步骤6：通过对模型进行多次的参数调整，得到最佳的模型状态，提高模型预测新数据的准确率。

2.2.2 增加房屋面积特征来估计家庭年收入

步骤1：选取电力特征和房屋面积特征共14个维度的特征，组成数据样本X，将样本家庭的年收入类别作为要预测的目标y。

步骤2：采用同样的方法对测试集的样本家庭年收入进行预测。

步骤3：与2.2.1节对比4种算法模型得到的分类准确率。

2.2.3 获取最优特征估计家庭年收入

考虑到2.2.2节中14个维度的特征可能存在由于维度过大而出现维度诅咒的问题，于是通过随机森林对特征重要性进行了评估，如图3所示。横坐标表示14个特征，纵坐标对应每个特征的重要性。从图3中可以看出，total square footage是最能区分类别的特征，std use和mean use次之。即重要性排名前三的特征是房屋面积、用电量标准差和用电量平均值。房屋面积和用电量往往正向相关，面积越大，用的电可能越多，这也从另一个角度说明了算法的有效性和合理性。

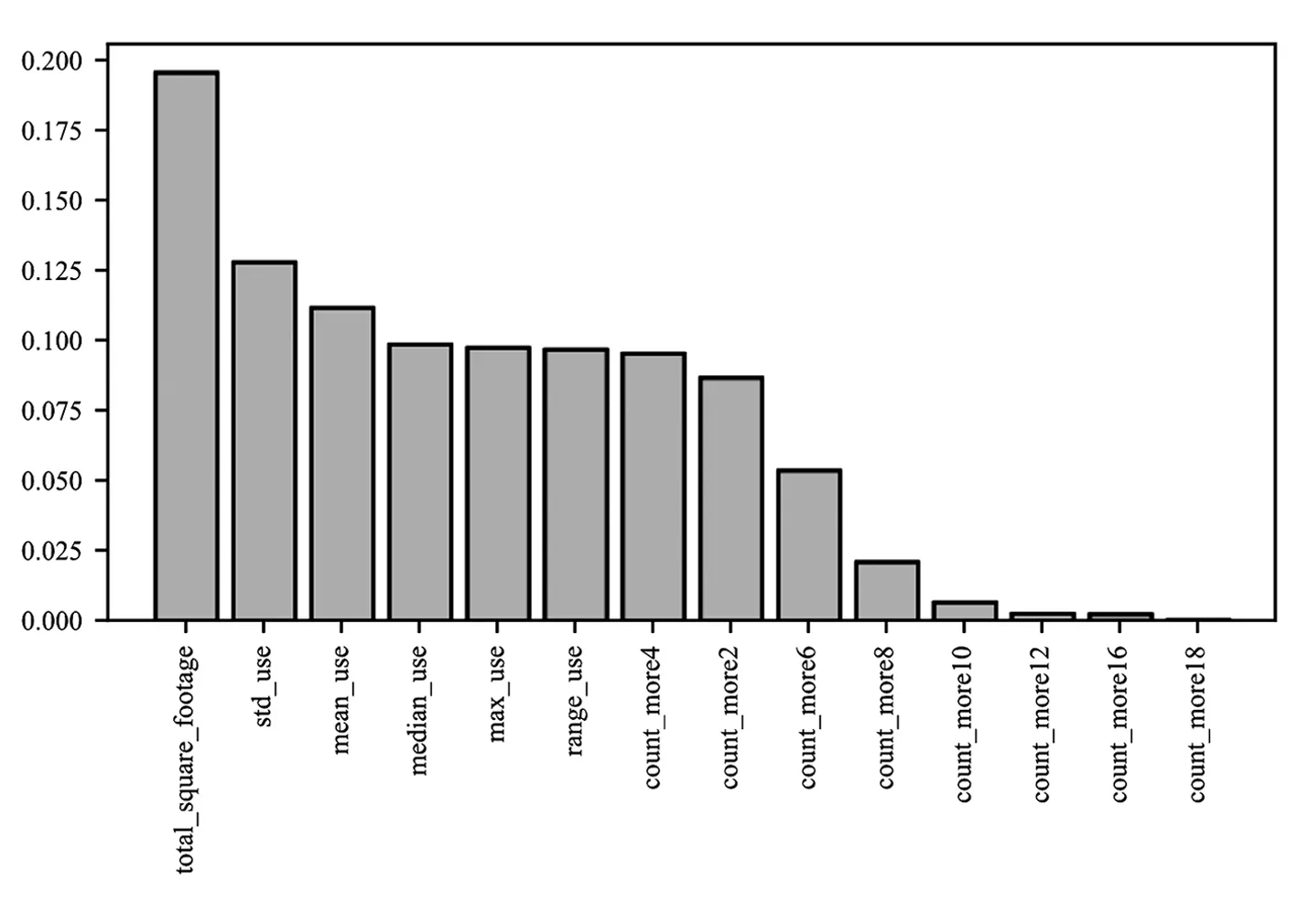
图3 特征重要性排序

此外，scikit-learn中的随机森林实现，还可以基于用户给定的阈值进行特征选择。设置阈值为0.09，最终便选择出7个维度的特征作为最优特征，即房屋面积、该年中家庭总用电量的标准差、平均值、中位数、最大值、极差和该年中每小时的家庭总用电量超过4 kW的时数。

得到最优特征之后，采用同样的方法对测试集的样本家庭年收入进行预测，与2.2.2节中不进行特征选择得到的分类准确率进行对比，验证维度诅咒的问题是否存在。

3 实验结果与分析

在图4中，黑色代表只使用家庭总用电量数据来估计家庭年收入的分类准确率，白色代表增加房屋面积特征后的分类准确率。从图4中可以看出，只使用总用电量数据，4种算法的分类准确率都很低，其中KNN的准确率相对来说是最高的，核SVM次之。在增加了房屋面积特征后，4种算法的分类准确率普遍有了很大幅度的提高。其中，使用核SVM对家庭年收入的分类准确率提高了15%，分类效果明显。其次是决策树算法，使分类准确率提高了13%。而线性SVM的分类准确率虽然也提高了，却始终是4种分类算法中准确率最低的。可见，增加房屋面积的信息，确实能够提高对家庭收入估计的准确率。此外，图4也验证了2.1节中所述的从分类算法本身的优缺点出发来选择算法的合理性，即线性SVM的确不适用于所提出的数据分析。

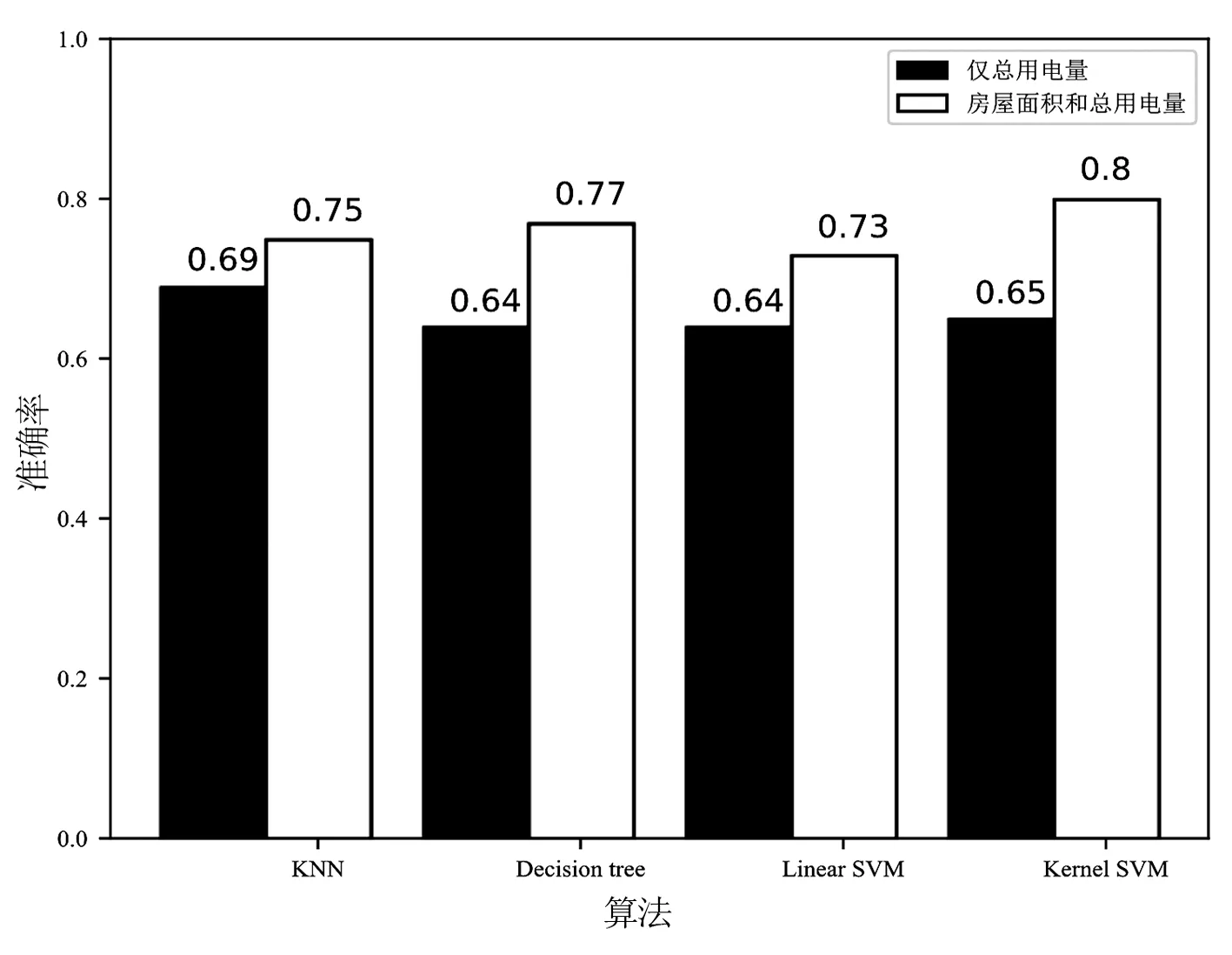
图4 增加房屋面积特征前后的分类准确率对比

在图5中，白色代表特征选择之前使用14个维度的特征估计家庭年收入的分类准确率，灰色代表特征选择之后使用7个最优特征估计家庭年收入的分类准确率。从图5中可以看出，经过特征选择，4种分类算法的准确率都有所提高，但是提高的幅度并不大，只有1%～2%。此外，核SVM依然是4种分类算法中估计家庭年收入准确率最高的，可以达到0.81，决策树算法次之，线性SVM的准确率最低。而KNN算法的准确率时高时低，可能与所采用的数据样本容量较小以及样本类别不平衡等因素有关。

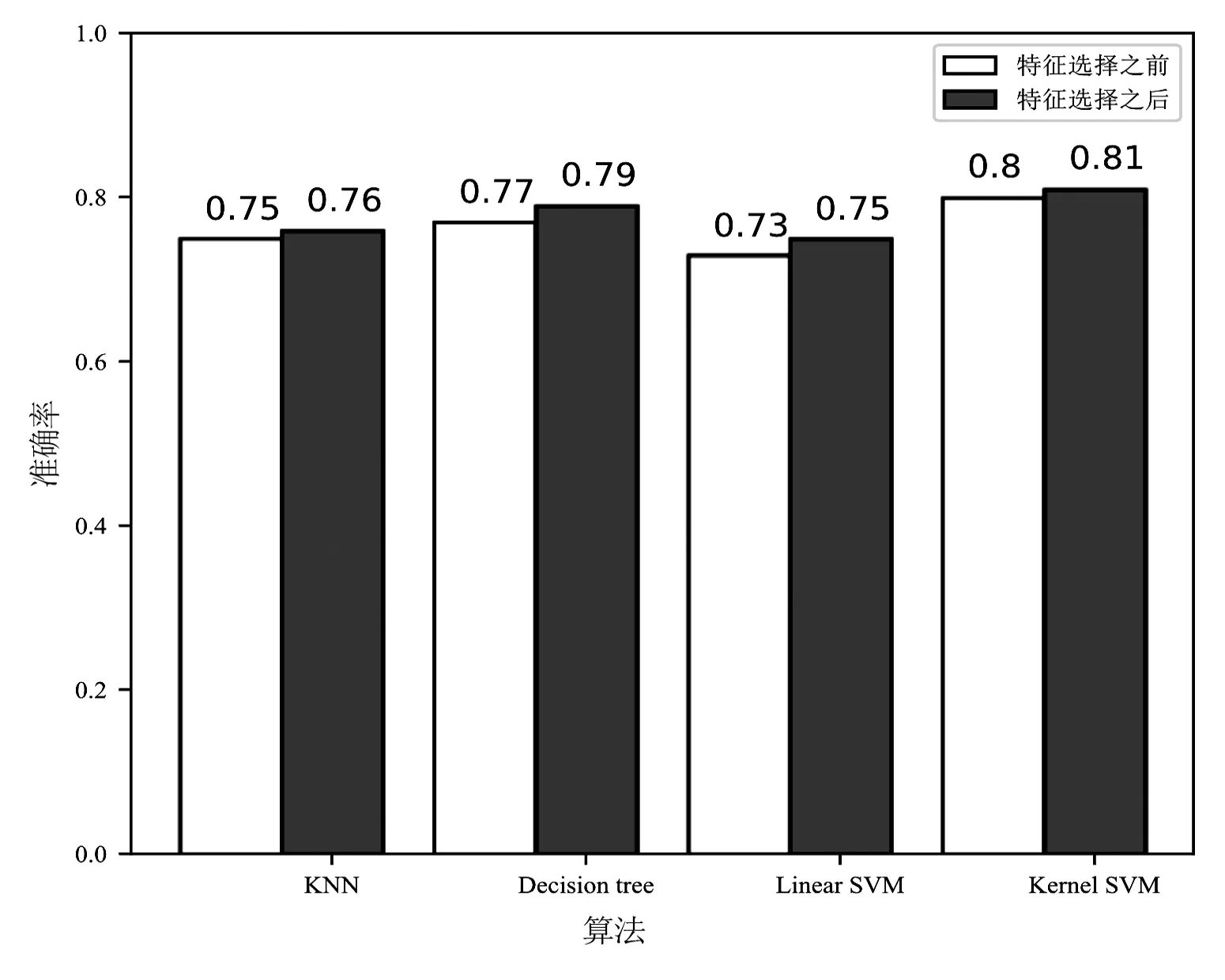
图5 最优特征选择前后的分类准确率对比

4 结 语

经过前面的研究得出以下结论：只使用总用电量信息对家庭收入估计的准确率相对较低；加入房屋面积信息之后，即使使用最基本的分类算法，也能大幅度提高对家庭收入估计的准确率。另外，在提出的4种基本的机器学习分类算法中，核SVM对于非线性可分数据的分类效果最好，决策树次之。

房屋面积信息作为房屋的一个最为明显的静态特性，不会因为受到外界影响而发生改变，具有稳定性和易捕获性的优点。用电量信息作为当今家庭中非常重要的信息之一，具有实时性的特点。综合这两种信息来推断家庭收入，无疑为今后的研究工作开拓了思路。所选用的是总用电量的信息，今后还可以尝试使用分解后各个用电器的用电量信息进行数据融合。将家庭收入划分为两个类别，今后可以尝试对家庭收入的类别作更精细的划分。同时，选用的算法仍需要不断的优化和完善。另外，所选用的数据样本规模偏小，普适意义还有待进一步提升样本规模，也是一个日后有待解决的问题[14]。

致谢

西南交通大学电气工程学院的郑珺老师和张雪霞老师在论文的结构、撰写和算法应用方面提出了指导性建议，谨此深表感谢。