风电场超短期风电功率预测研究

(1.新疆大学电气工程学院，新疆 乌鲁木齐 830047；2.山东岱盟电力工程咨询有限公司，山东 济南 250000)

0 引 言

近年来全球风机装机容量增长迅速，然而风电场输出功率波动性和随机性特点[1]，给电力系统的并网运行带来巨大挑战。为了确保电力系统运行的安全稳定可靠，缓解电力系统调峰和调频压力，必须提高风功率预测精度[2]。

目前，国内外风功率预测的方法主要有两类。一类是物理预测方法：此方法需要考虑地形和位置等地理信息以及风向、气压和温湿度等气象信息[3]，并与物理数值天气预报有机结合来进行风功率预测[4]；但是此方法计算量大、计算时间长且物理数值天气预报更新速度慢，从而较难得到准确的风功率预测值。另一类是统计预测方法：这类方法是现在研究最多的风功率预测方法，主要通过风电场的历史数据结合智能算法建立预测模型。预测模型主要有神经网络模型[5]、支持向量机模型[6]、马尔科夫链模型[7]等。文献[8]介绍了统计学习法基于机器学习的思想，弥补了统计法的不足，提高了模型的灵活性。文献[9]采用最小二乘向量机方法进行风速预测建模时，选择了径向基核函数，但是预测精度有待进一步提高。文献[10]采用遗传算法对支持向量机的惩罚因子和核函数参数进行优化选取，建立了GA-SVM模型，但遗传算法的迭代收敛速度仍有待提高。

下面将鲸鱼算法(whale optimization algorithm, WOA)和最小二乘支持向量机(least squares support vector machine, LSSVM)方法相结合，提出了基于WOA-LSSVM的组合预测模型。采用鲸鱼算法优化LSSVM预测模型最小二乘支持向量机可调参数，可有效提高预测精度。

1 理论基础

1.1 最小二乘支持向量机

支持向量机(support vector machine, SVM)解决的是不等式约束的二次规划问题，而最小二乘支持向量机是把解二次规划问题转化为求解线性方程组问题，将不等式约束条件变为等式约束条件，从而方便了Lagrange乘子α的求解，提高了收敛速度。

给定训练样本

T={(x1,y1),…(xi,yi),…(xl,yl)}∈(X,Y)l

其中，xi∈X=Rn为输入，yi∈Y=R为输出，构造支持向量机预测模型为

f(x)=ωTφ(x)+b

(1)

式中：ω为权向量；b为偏差。

支持向量机的等式约束为

(2)

s.tyi=ωTφ(xi)+b+ξi

i=1,2,…,n

(3)

式中：c为惩罚参数；ξi为松弛变量；n为训练样本长度；φ(xi)为训练样本的非线性变换。

采用Lagrange乘数法将原问题转化为对参数α求极值的问题，如式(4)所示。

L(ω,b,ξ,α)=

(4)

对式(4)中参数ω、b、ξ、α分别求偏导,令其等0，如式(5)所示。

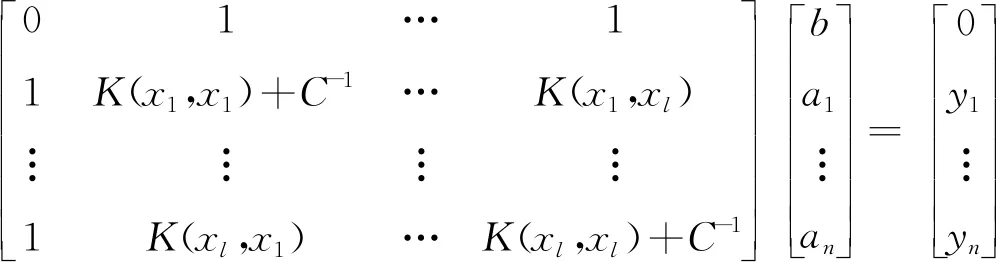
(5)

式中:核函数K(xi,xj)=f(xi,xj)是满足Mercer条件的对称阵，j=1,2,…,l。最终得到LSSVM的线性分类表达式为

(6)

LSSVM常用的核函数有径向基函数、多项式函数、Sigmoid函数、线性函数等。核函数类型及其参数的不同会对LSSVM回归性能有很大的影响。文献[11]采用8种核函数LSSVM预测模型，并对8种核函数的风电功率预测模型的预测误差进行比较，得出基于径向基函数(RBF核函数)的预测误差指标相对较小、预测精度更高。这里选用径向基核函数。

(7)

式中：σ为核函数参数；c为惩罚参数。从LSSVM建模过程可知，LSSVM预测性能受到核函数参数σ和惩罚参数c的影响较大，下面采用鲸鱼算法优化这两个参数，以提高风功率预测精度。

1.2 鲸鱼算法

鲸鱼算法[12]是澳大利亚学者Mirjalili于2016年提出的一种新的群体智能优化算法，作者受到座头鲸捕猎行为启发，模仿了座头鲸搜索猎物、包围捕猎和螺旋气泡网捕猎3个过程，最终提出鲸鱼算法。在鲸鱼算法中，每头座头鲸的位置就是要解决的可行解。具体捕猎步骤如下：

1)搜索猎物

座头鲸在寻找猎物时通过随机搜索猎物方法，不断更新自己的位置来达到捕猎食物的目的，如式(8)、式(9)所示。

D=|CXrand-X|

(8)

X(t+1)=Xrand-AD

(9)

式中，t为当前的迭代次数；Xrand为座头鲸随机的一个位置向量；X为位置向量；向量A和C为系数，其值为

A=2ar-a

(10)

C=2r

(11)

式中：a为从2到0逐渐递减的值；r为0到1间的随机值。

2)包围捕猎

座头鲸包围捕猎方式如式(12)、式(13)所示。

D=|CX*(t)-X(t)|

(12)

X(t+1)=X*(t)-AD

(13)

式中：X*(t)为当前最佳位置向量；X(t)为当前位置向量。

3)螺旋气泡网捕猎

座头鲸螺旋气泡网捕猎方式为

X(t+1)=D′eblcos(2πl)+X*(t)

(14)

式中：D′=|X*(t)-X(t)|为位置最佳座头鲸与猎物(目前最佳解)之间的距离；b为一个定义螺旋线形状的常数；l为-1到1之间的随机值。

座头鲸捕猎时，各以50%的概率选择上述两种捕猎方式，如式(15)、式(16)所示。

X(t+1)=X*(t)-ADp≤0.5

(15)

X(t+1)=D′eblcos(2πl)+X*(t)p≥0.5

(16)

由公式(10)可计算出A的取值范围为[-2,2]。

WOA算法相较于其他优化算法而言，优势在于操作简单、调节的参数少，只包含2个主要调节参数A和C。通过对A的设定，该算法能够更好地平衡开发和勘探能力，增大跳出局部最优的可能性，达到全局最优。WOA算法流程如下：

1)初始化参数：定义随机产生初始化座头鲸种群{Xi|i=1,2,…N}，N为种群规模，Tmax为最大迭代次数。

2)在可行域空间内随机初始化座头鲸种群的位置。

3)计算每一头座头鲸相应的适应度值，根据适应度值的大小排序，并选取N作为初始种群规模。

4)计算出N个个体适应度值的大小，找出适应度值最小的个体位置作为最优位置。

5)当A≥1时，采用式(13)更新下一代的位置；当A<1时，采用式(15)、式(16)来更新下一代的位置。

6)若达到终止条件，则输出最优个体，即算法找到的最优解；否则，返回步骤4)。

2 WOA-LSSVM预测模型建立

LSSVM有良好的非线性预测性能。基于以上特点建立WOA-LSSVM预测模型。建模步骤如下：

1)首先结合风电监控系统数据库中的历史功率数据和环境参数形成样本数据。

2)建立LSSVM风电功率预测模型。

3)采用鲸鱼算法优化核函数参数σ和惩罚参数c这两个参数，建立WOA-LSSVM模型，并进行风功率预测。

4)进行误差分析。

3 算例及结果分析

3.1 风电场风功率数据处理与分解

数据在采集和运行过程中会存在一些异常数据，严重影响风功率预测的精度。因此，需要对原始风功率数据进行预处理，将缺失的风功率数据补充完整。采用牛顿插值法补充缺失数据，有效保证能够符合预测模型的运行要求。选取某风电场2019年1月8日到1月11日的风功率数据作为原始风功率数据，时间跨度为3 d，采样时间为5 min，共计采取1152个数据点。把前3天风功率数据作为历史数据用来训练，第4天风功率数据作为预测的测试数据，系统记录的风功率时间序列曲线如图1所示。

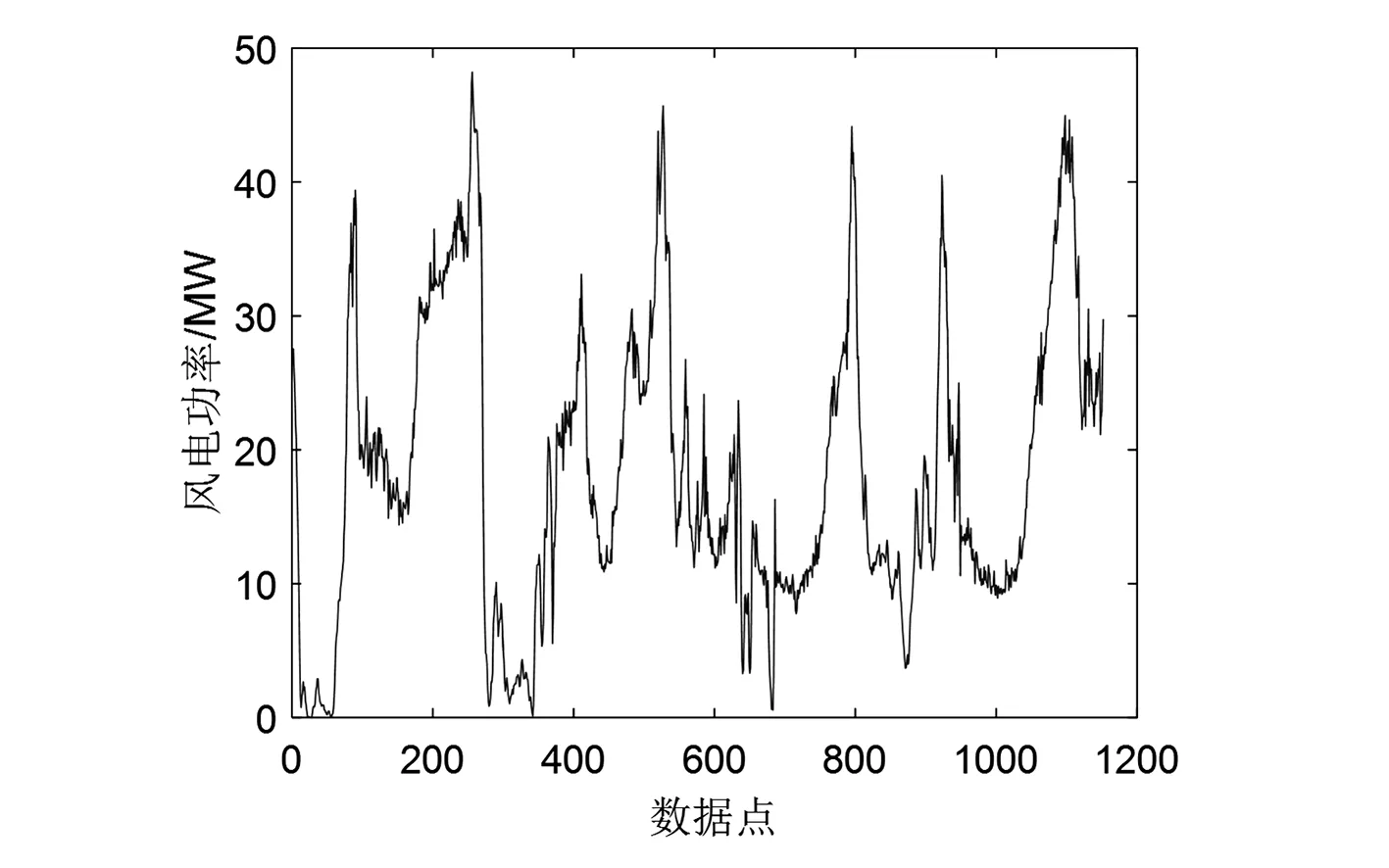
图1 风电场风功率时间序列

对预处理完成的1152个风功率数据，取前864个风功率数据样本点作为LSSVM模型训练集，后288个风功率数据样本点作为LSSVM模型测试集。

3.2 风功率短期预测结果分析

采用WOA算法优化预测模型中精度受到影响的2个参数：惩罚参数c和核函数参数σ，模型优化的参数如表1所示。

表1 参数优化结果

原始风功率时间序列经过鲸鱼算法优化最小二乘支持向量机参数，最终建立基于WOA-LSSVM的风功率预测模型。为了验证所提出的模型在预测精度上的优越性，还分别对LSSVM模型、GA-LSSVM模型和PSO-LSSVM模型进行风功率超短期预测，4种风功率预测结果如图2所示。

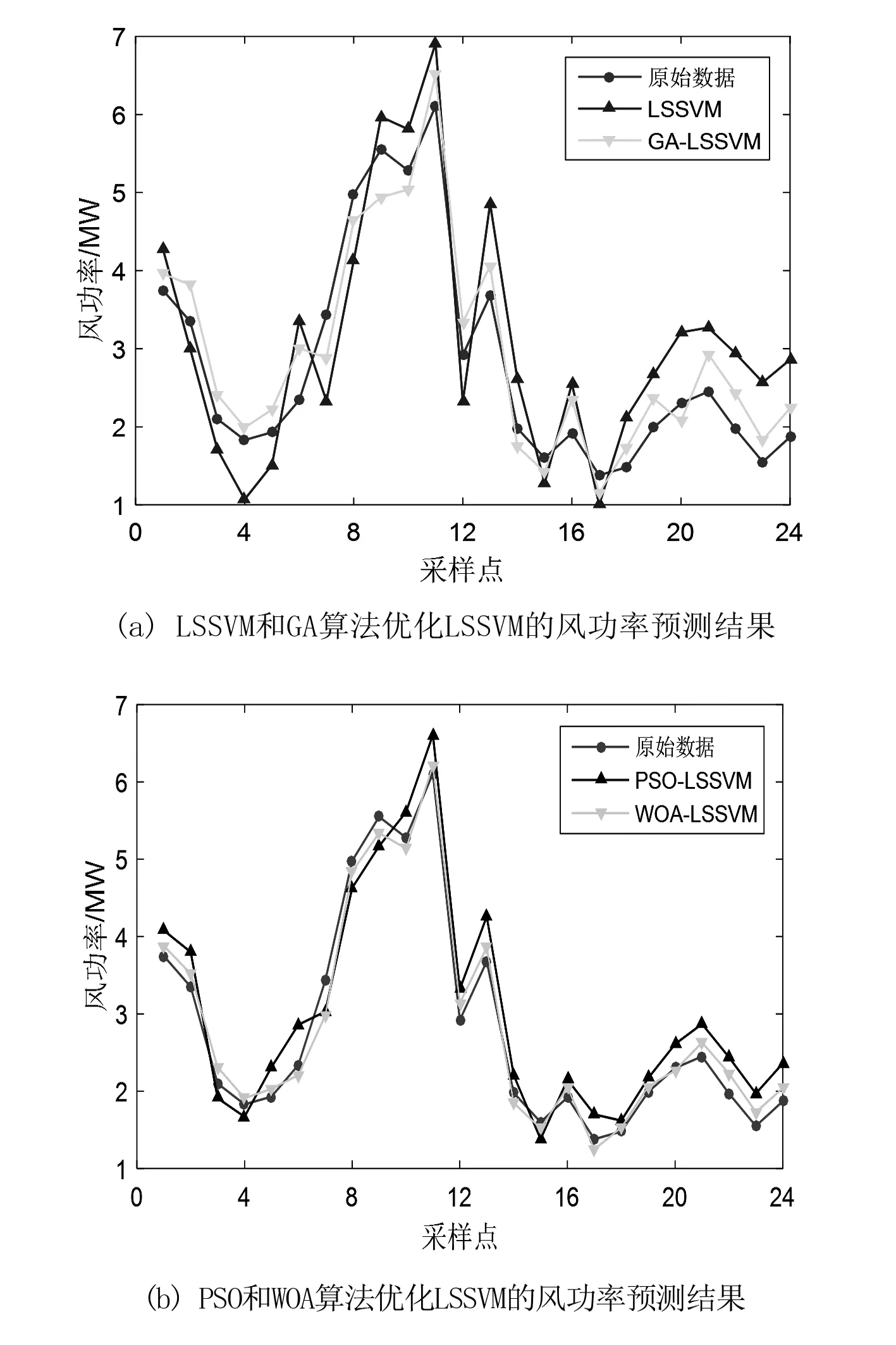
图2 4种模型风功率预测结果

由图2分析可知，基于WOA-LSSVM模型预测的精度更高，准确性更好。

为更好比较4种模型的预测效果，采用平均相对误差百分比(MAPE)及平均绝对误差(MAE)这2个误差指标来衡量预测精度，并对预测结果进行对比分析。

(17)

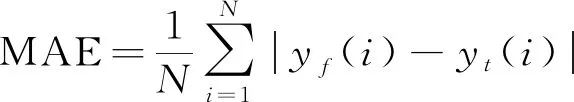
(18)

式中：N为采样点数；yf(i)为预测值；yt(i)为实际值，其风功率预测误差指标如表2所示。

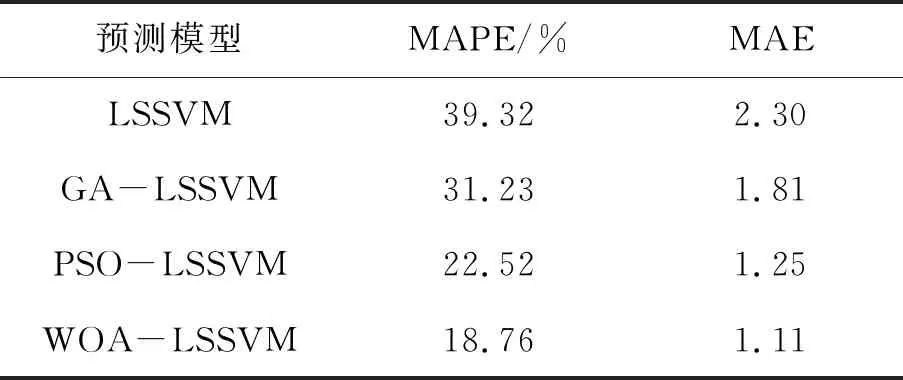
表2 4种模型误差评价指标结果

从图2和表2对比可知，4种风功率预测模型的差异性如下：

1)建立的WOA-LSSVM组合模型能够有效对原始的风功率曲线进行拟合，验证了建立模型的正确性。

2)建立的WOA-LSSVM组合模型与其他3个模型对比，WOA算法优化2个参数建立的LSSVM预测模型，预测精度更高，也验证了WOA算法对风功率预测是可行的。

3)从风电功率误差评价指标结果中看出，建立WOA-LSSVM组合模型的误差指标明显低于其余的3种预测误差值。

4 结 语

提出了一种基于鲸鱼算法优化最小二乘支持向量机参数的预测模型，并用于超短期风电功率预测。实验结果表明：与GA算法相比，所采用的WOA算法能够扩大搜索范围，提高收敛速度，减少迭代次数，能有效避免陷入局部极值。采用的WOA-LSSVM预测模型能够更好地实现风电功率的预测，也验证了所建模型的优越性。