基于贝叶斯准则的差异网络分析方法研究与应用*

哈尔滨医科大学卫生统计学教研室(150081) 宋 微 王文杰 徐 欢 蔡雨晴 李 康

【提 要】 目的 探讨基于贝叶斯准则的差异网络分析方法的性能，并将其应用于卵巢癌基因表达谱数据分析。方法 通过模拟实验评价其识别差异边及差异节点的准确性，并与传统方法做对比。同时应用上皮性卵巢癌基因组学数据，构建差异网络模型。结果 模拟试验结果表明，基于贝叶斯准则的差异网络分析方法识别差异边能力明显优于高斯图模型方法；实例分析结果表明，本文方法构建的差异网络模型具有实际意义。结论 应用基于贝叶斯准则的差异网络分析方法能得出准确度较高的差异网络，效果优于传统方法。

基因的作用通常不是独立的，而是基因之间相互影响、相互制约，形成复杂的基因调控网络。某些疾病发生时，基因表达量变化不明显，而基因网络中调控关系却发生明显改变，这种情况传统的差异分析方法通常无法识别。而在实验条件下，由于独立误差、人为因素、试验条件限制等原因，有些差异调控关系往往不能被研究者发现。然而，在大数据网络结构分析中便可被发现具有统计学显著性。因此，在疾病研究领域，差异网络的研究已越来越受到研究者的重视。目前最常用的基因调控网络模型有布尔网络模型、线性组合模型、加权矩阵模型、高斯图模型和贝叶斯网络模型等[1-2]。其中图模型是在变量条件独立的情况下构建基因网络，排除了其他变量的影响，因此能在复杂的相互关系中准确提取出两变量间的真实调控关系。贝叶斯因子(Bayes factor,BF)是基于贝叶斯准则研究得出的方法，广泛用于模型比较，通过计算BF可得出差异模型的直接证据。本文将高斯图模型与贝叶斯准则相结合，建立差异网络模型，推断出网络中差异的调控关系，并与一般的高斯图模型方法相比较，考察其有效性。最后运用本文给出的方法对卵巢癌基因表达谱数据进行分析，做出生物学解释。

原理与方法

1.高斯图模型

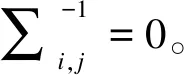
(1)

基于以上高斯理论，当ρXiXj|X-i,-j≠0时，变量i与变量j之间的边存在于高斯图模型中。

在处理高维组学数据时，往往会遇到“m≪n”的问题，即变量数m远大于样本数n，此时协方差矩阵不是唯一的，因此传统的统计模型无法求出偏相关系数。针对此种情况，有学者提出应用调整回归模型推导两变量的偏相关系数，将变量Xi作为因变量，剩余变量Xj(j≠i)作为自变量，构建回归方程：

(2)

(3)

(4)

ρXiXj|X-i,-j=

(5)

2.差异网络分析

为推断不同条件下网络中的差异结构，将含有m个变量的数据按K个分类标签分成不同数据集。对于公式(2)，记Y=Xi。根据极大似然和平均场近似估计理论，可以直接得出K个独立网络结构满足：

(6)

对于给定的模型M(分类)，基于模型参数的变分推断方法，结合变分下限和可逆跳跃马尔科夫链蒙特卡洛方法(RJMCMC)[4]，可以求得模型证据p(X|M)的估计值：

(7)

公式中X表示模型中所有变量的观察值，θ代表所有模型参数的集合。对于K=1和K=2两个模型，通过计算贝叶斯因子

(8)

判断支持哪个模型成立的证据更为充分，即各变量(如基因)对其他变量调控关系在两类中是否有显著的差异。对每个变量X1,……，Xm计算贝叶斯因子，如果大于给定阈值，则进一步根据偏相关系数判断差异边，最后根据给定的假发现率FDR值判定网络中的调控边，得出差异网络。

模拟实验

研究通过对设置的网络结构偏相关系数矩阵的运算产生不同样本量的模拟数据[2]。检验基于贝叶斯准则的差异网络分析方法(记为Bayes)，将贝叶斯因子选择的差异网络模型与设置的真实差异网络结构进行比较，若分析结果能够获得更多的已知差异网络中存在的边，则说明该方法有更好的分析效果。根据前期研究结果和大量文献经验结果，本模拟取BF(i)>2和FDR<0.025。

模拟产生两组数据，网络中共包含50个节点，其中有6个为差异节点(G30、G38、G1、G37、G4、G42)，共有49条共同边和8条差异边(黑色)，49条共同边偏相关系数在(-1,1)随机抽取，8条差异边的偏相关系数在(0.2,0.5)随机抽取。黑色边上的数字“1”和“2”分别表示两种不同情况下网络中的差异边。数字“1”为仅在第一组数据中有调控关系，数字“2”为仅在第二组数据中有调控关系(参见图1和表1)。模拟选取样本量n1=n2={30,60,90,120,150}，模拟实验重复100次。

图1 模拟实验1设置的真实差异网络关系图

差异边节点1节点2第一组第二组1G30G1102G30G4103G30G37104G30G42105G38G1016G38G4017G38G37018G38G4201

对数据分别使用Bayes、GeneNet、FastGGM三种方法进行分析，其中后两种方法是两种常用的高斯图模型方法[2,5]。模型的评价指标选用准确度、假发现率、灵敏度和特异度，其中准确度为真阳性边占检查出的阳性边的比例，相当于诊断试验中的阳性预测值，假发现率为假阳性边占检查出的阳性边的比例。Bayes方法模拟实验结果显示在图2中，可以看到：每组样本量为60时，准确度维持在0.6左右；在每组样本量为90时，差异节点的灵敏度达到1，差异边的灵敏度在0.75附近。图3显示了三种不同方法在不同样本量下的准确度和假发现率，可以看到，Bayes方法明显优于另外两种常用的方法。

图2 模拟实验各评价指标随样本量不同的变化情况

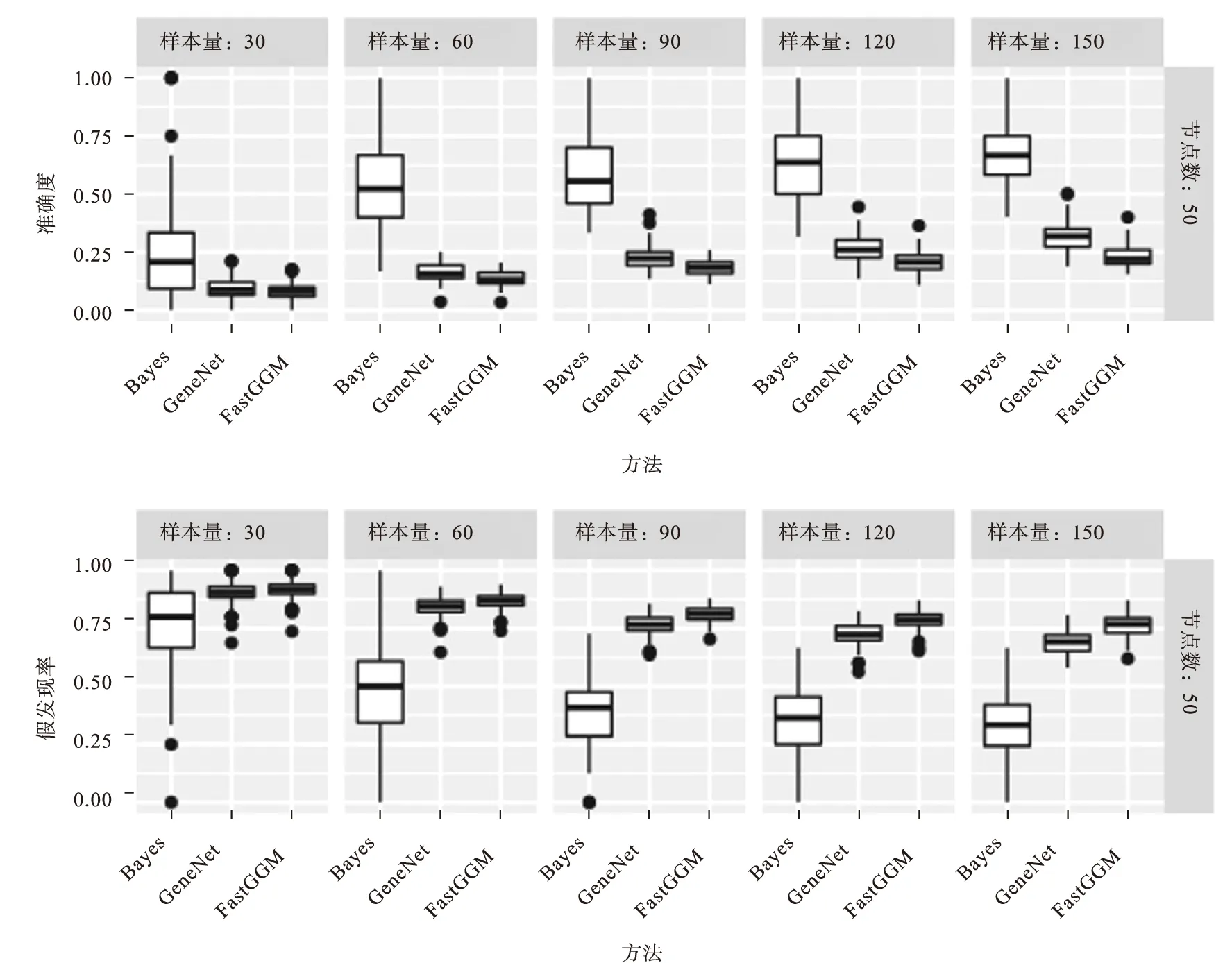
图3 三种方法在不同样本量下准确度和假发现率箱式图

实例分析

本研究通过对卵巢癌患者复发情况及基因表达数据进行分析，应用基于贝叶斯准则的差异网络分析方法构建差异网络模型，得出基因间差异调控关系，及存在差异调控关系的基因。通过结合生物学知识、通路数据库、文献查询，对差异网络结果进行生物学解释，从基因组学角度为卵巢癌复发机制提供线索。

本研究从R包curatedOvarianData (version:1.8.0)中下载Ⅱ-Ⅳ期上皮性卵巢癌患者基因表达谱数据(GSE49997)，排除了临床信息中缺失复发时间以及复发时间<90天的患者，基因表达数据应用Z-score法进行标准化。将患者根据生存情况分为复发组124例和非复发组70例，全基因组表达谱数据一共测得16024个基因的表达值。由于基因数目过多，需要先筛选出与上皮性卵巢癌复发相关的基因通路，再对通路中的全部基因构建差异网络模型。变量筛选有助于提高建模效率，使得差异网络模型更加合理。本研究使用基于LASSO的Cox比例风险回归模型，对通路富集后的基因进行得分计算，并通过得分矩阵对通路进行筛选[6]，最终给出与卵巢癌复发有相关的12条通路。其中，FoxO信号通路经动物实验证明有抑癌作用[7]，同时，研究表明FoxO蛋白表达量与卵巢癌生存期相关[8]。基于以上结果，本研究选取FoxO信号通路中全部基因，在复发组和非复发组中进行差异网络模型的构建与分析。

将映射在FoxO信号通路中的119个基因的表达数据整理出来，标准化处理后结合复发状态数据进行差异网络模型的构建。应用基于贝叶斯准则的差异网络分析方法构建差异网络模型，结果如图4所示，其中节点代表FoxO信号通路中的基因，黑色虚线代表复发与非复发状态下的共同边，13条黑色虚线代表只存在于复发患者中的差异边，9条黑色实线则代表只存在于非复发患者中的差异边(表2)。存在差异调控关系的基因如表3所示，其对应的差异调控关系频数越大，越可能成为差异网络中的枢纽基因(Hub Gene)。

图4 卵巢癌患者复发与非复发状态下的差异基因调控网络

通过查询GeneMANIA及KEGG基因数据库，发现有8条差异边出现在数据库中，例如NLK与PRKAA1、FOXO4和SGK2三个基因间的调控关系。表3中NLK、STK4、HOMER1、PRKAA1、EGFR五个基因与多个基因间存在差异调控关系，可以将他们视为差异网络中的枢纽基因。有文献报道NLK与卵巢癌分期、分级、化疗和预后有关，NLK基因的高表达加速了顺铂治疗中的细胞凋亡过程，从而延长病人生存期[9]。另一枢纽基因EGFR与肿瘤细胞的增殖、血管生成、肿瘤侵袭、转移及细胞凋亡的抑制有关，EGFR的表达水平可作为上皮性卵巢癌患者生存期的预后因子，其高表达与生存期的降低相关[10]。

表2 卵巢癌患者复发状态差异网络中的差异调控关系

表3 卵巢癌患者复发状态差异网络中的差异基因及其对应的差异调控关系频数

讨 论

传统变量筛选方法主要针对不同条件下基因表达量的差异，无法准确识别表达量未发生明显变化但调控关系改变的基因。基于贝叶斯准则的差异网络分析方法是在高斯图模型基础上，给出的一种能够识别不同条件下调控关系改变的变量和调控边的一种方法。该方法利用贝叶斯原理，在假定的先验分布上对模型的参数进行估计，获得偏相关系数，在此基础上从整体网络的角度进行差异推断。

模拟实验结果表明，差异贝叶斯方法具有较好的识别差异边的能力，本研究得到以下几点结论：①基于贝叶斯准则的差异网络分析方法结果可靠，即在保证高准确度的同时，还具有较低假发现率的特点；②该方法受样本量的影响较小，在样本量小于变量数的情况下也能识别差异网络中的差异调控关系；③传统的高斯图模型推断差异网络时，需要在不同情况下单独建网后比较差异边，相比之下，加入贝叶斯因子进行模型选择，提高了高斯图模型识别差异边的能力。

通过实例分析，对上皮性卵巢癌复发和非复发的调控网络进行了对比，得出两组在FOXO信号通路中差异调控关系及差异网络的枢纽基因，为卵巢癌复发的基因调整网络机制的研究提供了线索。

应用该方法理论上对变量的数目没有限制，因此适用任何差异基因调控网络的比较，并能准确地进行差异调控边的定位。这种方法可以通过贝叶斯因子得出差异模型证据，进而从数值上检验差异存在的可能性大小。然而，生物网络通常是非常复杂的，要确证不同条件下的真实差异调控关系，还必须通过生物学实验进行验证。