小学数学活动课“扑克牌中的奥秘”教学实录
史颖慧
适用年级:
四年级上册
配合进度:
北师大版小学数学四年级上册第七单元“可能性”。
活动目标:
1.加深理解和掌握随机现象发生的可能性是有大有小的。
2.初步了解可以用分数来表示可能性的大小。
3.理解和掌握用逐一列举的方法解决数学问题。
4.提高学生团结合作的能力,激发学生学习数学的兴趣。
活动准备:
扑克牌、课件、记录表。
活动过程:
一、魔术表演 ,激趣引入
师:同学们,你们喜欢看魔术表演吗?
生:喜欢。
师:老师给同学们变一个魔术,想不想看?
生:想。
师:我想请一名同学和我一起变这个魔术,谁愿意?
(将扑克牌洗匀,让学生随机抽一张,并记住它是什么牌。学生将这张牌放回整副牌中,老师重新快速洗牌后,可以迅速地把这张牌找回。)
师:魔术里面蕴藏着许多的奥秘,很神奇。其实扑克牌还蕴藏着许多数学奥秘,那今天我们就用扑克牌探索与数学有关的奥秘。(板书课题)
二、扑克游戏,寻找奥秘
1.介绍游戏规则
师:这节课我们将通过游戏的形式来探索其中的奥秘,在游戏之前,我们要知道什么?
生:游戏规则。
师:没错,接下来请同学们仔细分析游戏规则。
(动画播放)介绍规则:
(1)6个人一小组玩游戏,1个人当庄家、1个人当记录员、另外4个人当玩家。
(2)庄家准备好3张扑克牌,分别是1张大王和2张小王,将这三张扑克牌打乱后反扣在桌面上。
(3)4个玩家轮流跟庄家玩游戏,玩家从桌面上任选1张牌(不许翻看正面是什么牌),庄家从剩下的2张扑克牌中拿走1张小王。
(4)此时,在桌面上庄家和玩家各有1张牌。玩家可选择将自己的牌与庄家交换,也可选择不换。
(5)最后看大王在谁的手里,如果玩家手上的牌是大王,则玩家胜,若不是则庄家胜。
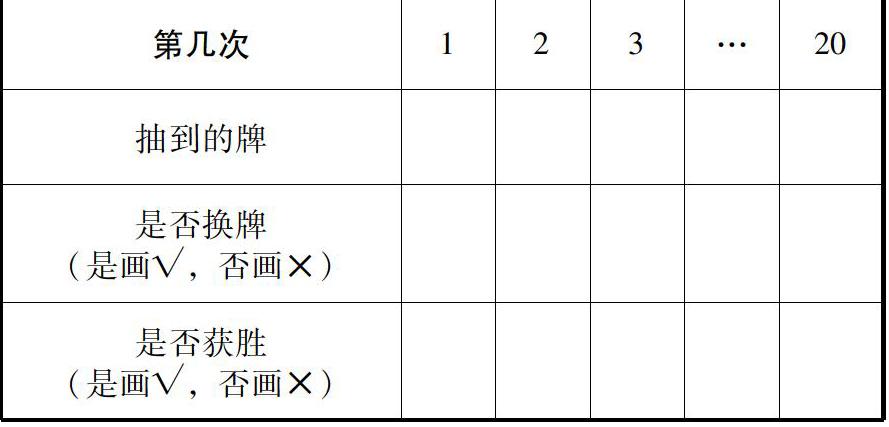
(6)每一轮游戏结束后,记录员将结果记录在下面的表格中。
师:我想找两位同学上来跟我试着玩一下,谁愿意?
(两名学生上台与教师合作示范玩游戏,让全班同学直观感受,清楚游戏的具体玩法。)
2.开展游戏活动
师:同学们,你们看懂游戏规则了吗?想玩吗?
生:清楚了,想玩。
师:这节是数学课,我们要学会用数学的眼光来玩游戏。所以,在游戏的过程中,请同学们思考一个问题:玩家怎么玩才容易获胜呢?(课件显示该问题)
(学生开始游戏,教师参与。)
3.分析記录数据
师:刚才看到同学们玩的热火朝天,不知有没有悟出其中的奥秘。下面请每个小组整理下你们的记录表,分析下你们记录的数据,看看会有什么发现。
(学生讨论,教师参与。)
师:哪个小组愿意与大家分享你们发现的结果?
组1:我们组玩家共有12次选择换牌,其中只有5次获胜。从中我们可以得出,玩家选择不换牌,获胜的机会大一些。请问同学们,你们有质疑和补充的吗?
组2:我们小组的结果跟你们不一样,我们组玩家共有10次选择换牌,其中有7次获胜。从中我们可以得出,玩家选择换牌,获胜的机会大一些。
师:现在出现了两种不同的意见,请问其他小组,你们赞成哪个小组。请赞成第一组的举手。
(学生统计各自的数据,并决定赞成哪个小组。)
4.分析游戏奥秘
师:8个小组中,共有6个小组觉得玩家选择换牌容易获胜,还有两个小组不同意。那究竟该如何选择才容易获胜,这就需要我们深入地分析这背后的奥秘。哪个小组同学能深入地分析这背后的原因吗?
组4:我们觉得玩家选择换牌或不换牌,获胜的可能性一样大。因为庄家把小王拿走之后,剩下的那张牌不是大王、就是小王,它们的可能性是一样大的,能否获胜主要看运气。
组2:我们反对,第4组的这种想法,忽略了玩家的那张牌是从3张牌中随机摸出来的。刚开始,庄家一共有3张牌,1张大王,2张小王,在玩家摸到的牌中,摸到小王的可能性大些,庄家手中剩大王的可能性大,所以玩家选择换牌,赢的可能性大。
师:你们能明白第2组的说法吗?哪个同学能再说说?
生:一共有3张牌,其中2张小王,玩家随机从3张牌中摸出1张,摸到小王的可能性是3份中的2份,所以玩家选择换牌,赢的可能性大。
师:你们同意这种说法吗?
生齐答:同意。
师:为了清楚地表示出摸牌的过程,我们可以把可能出现的情况逐一列举出来。
师生共同填写下表。
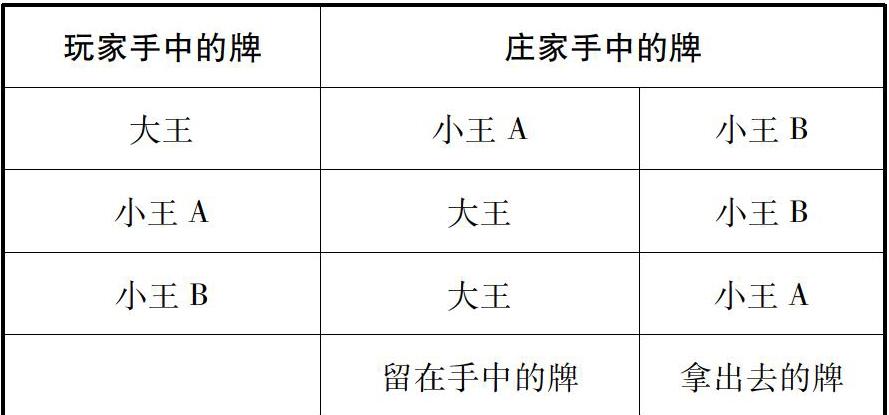
师:有哪位同学能借助这个表格,再来说一说这个游戏的奥秘吗?
生:从这个表中我们可以看出,庄家拿走手中的那张小王之后,留在手中的牌,共有3种情况,其中有2种是大王在手上,所以玩家选择换牌的可能性大,是3份中的2份,可以用三分之二来表示这个可能性的大小。
师:不是说玩家选择换牌,获胜的可能性大吗,那为什么会出现刚才的第1组同学正好相反的数据出现呢?
生:虽然说玩家选择换牌,获胜的可能性大,但是,选择换牌,也不一定说就一定会获胜。这里面还是有运气在的。
师:从理论上分析,的确是选择换牌,玩家容易获胜。但是玩家不换牌,也还是有可能获胜的,这时靠的就是运气了。
师:刚才,我们是通过一一列举的方法,把所有的情况都逐个列举出来,再从中分析、找到游戏奥秘的。其实这样的方法,在数学学习中经常会用到,我们把这样的方法叫逐一列举法。(板书:逐一列举)
(二)猜反面游戏
师:同学们,还想玩游戏吗?
生:想!
师:接下来,我们将刚才这个游戏进行升级,你们敢接受挑战吗?
生:敢!
1.介绍游戏规则
(1)6个人一小组玩游戏,1个人当庄家、1个人当记录员、另外4个人当玩家。
(2)庄家准备6张扑克牌,3张大王、3张小王。把每2张牌背对背贴在一起,制作成3张新牌,3张新牌的两面分别是:大王—大王、小王—小王、大王—小王。
(3)庄家将这三张新牌放在一个信封当中,打乱顺序,请玩家任意抽取一张放在桌面,不能看背面是什么牌。
(4)玩家猜一猜,摸出的那张牌的背面是什么牌,猜对了则玩家获胜,否则庄家胜。
师:同学们,你们听懂游戏规则了吗?那我找三位学生上来试玩一次?
学生演示游戏。
2.分析获胜策略
师:同学们,你们想不想也来玩这个游戏?
生:想。
师:玩家们想不想在游戏中打败庄家。
生:想。
师:那么这个游戏我们先不着急玩,我们先来研究其中的奥秘。为了便于研究,我将这三张新牌复原为6张牌,并为它们编好号,分别是:大A、大B、小A、小B、大C,小C。
师:我们同样以小组为单位讨论出其中的奥秘,并思考大屏幕上的问题:玩家怎么猜,更容易获胜?
同学们可以在纸上画一画,写一写。建议你们还可以参考刚学过的逐一列举的方法来寻找获胜的秘诀。
学生讨论,教师参与。
师:哪个小组愿意先分享你们的发现?
组1:
假设我们抽到的牌正面是大王A,则反面是大王B;正面是小王A,则反面是小王B;正面是大王C,则反面是小王C。正面是大王的有两种情况,它们的反面一個是大王、一个是小王,所以看到正面是大王,猜测背面是大王和猜测背面是小王赢的可能性一样大。
组2:我反对,第一组并没有把所有情况都列举出来。假设我们抽到的牌正面是大王A,则反面是大王B;正面是大王B,则反面是大王A;正面是小王A,则反面是小王B;正面是小王B,则反面是小王A;正面是大王C,则反面是小王C;正面是小王C,则反面是大王C。
师:你一共列举了多少种情况?
生:6种。
师:你继续讲你的发现。
生:从这6中可以看出,假设我们抽到的是大王,我们猜测大王赢的可能大,若抽到小王,我们猜测小王赢的可能性大。
师:同学们,你们听懂他讲的了吗?
生:不论是抽到大王还是小王,猜测正反面相同的,赢的可能性会更大。
师:哇,老师为你点一个大大赞,你总结的真棒。
3.试玩游戏
师:同学们,接下来就请你们试一试这个游戏,检验下刚才发现的奥妙是否正确。
(生游戏,师参与。)
三、活动总结,梳理提升
1.游戏来源
师:同学们,其实这个游戏来源于美国的一个电视节目,叫做三扇门问题。有3个完全一样的门,其中一个后边藏着一辆汽车,另外两扇后边各有一只羊,现在让观众选择一个门,主持人在另外两扇门中打开了一扇,观众看到里边是一只羊,此时再给他一次选择的机会,可以坚持原来的选择,也可以改选另外一扇没有打开的门。如果观众最后拿到的是车,就可以把车带走了。同学们给这个参赛者一点意见,是选择换还是不换呢?
生:换。
师:这样可以把车带回去的可能性会更大。
2.全课总结
师:我们这节课就是把这三扇门的问题利用了扑克牌去研究的,并且我们研究其中的奥秘就是可能性的大小,我们通过把所有出现的情况一一罗列,逐一列举,找到扑克牌中的奥秘,解决了有关可能性的问题。其实可能性在我们生活当中随处可见,只要同学们善于观察,善于思考,就会发现我们身边有很多有趣的数学问题。
责任编辑 龙建刚

